Rock Mechanics –! Response of Rocks to Applied Loads!
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Copyright Notice
COPYRIGHT NOTICE The following document is subject to copyright agreements. The attached copy is provided for your personal use on the understanding that you will not distribute it and that you will not include it in other published documents. Dr Evert Hoek Evert Hoek Consulting Engineer Inc. 3034 Edgemont Boulevard P.O. Box 75516 North Vancouver, B.C. Canada V7R 4X1 Email: [email protected] Support Decision Criteria for Tunnels in Fault Zones Andreas Goricki, Nikos Rachaniotis, Evert Hoek, Paul Marinos, Stefanos Tsotsos and Wulf Schubert Proceedings of the 55th Geomechanics Colloquium, Salsberg Published in Felsbau, 24/5, 2006. Goricki et al. (2006) 22 Support decision criteria for tunnels in fault zones Support Decision Criteria for Tunnels in Fault Zones Abstract A procedure for the application of designed support measures for tunnelling in fault zones with squeezing potential is presented in this paper. Criteria for the support decision based on quantitative parameters are defined. These criteria provide an objective basis for the assignment of the designed support categories to the actual ground conditions. Besides the explanation of the criteria and the implementation into the general geomechanical design process an example from the Egnatia Odos project in Greece is given. The Metsovo tunnel is located in a geomechanical difficult area including fault zones and a major thrust zone with high overburden. Focusing on squeezing sections of this tunnel project the application of the support decision criteria is shown. Introduction Tunnelling in fault zones in general is associated with frequently changing ground and ground water conditions together with large and occasionally long lasting displacements. -

Compressive Behavior Characteristics of High-Performance Slurry-Infiltrated Fiber-Reinforced Cementitious Composites (Sifrccs) Under Uniaxial Compressive Stress
materials Article Compressive Behavior Characteristics of High-Performance Slurry-Infiltrated Fiber-Reinforced Cementitious Composites (SIFRCCs) under Uniaxial Compressive Stress Seungwon Kim 1 , Seungyeon Han 2, Cheolwoo Park 1,* and Kyong-Ku Yun 2,* 1 Department of Civil Engineering, Kangwon National University, 346 Jungang-ro, Samcheok 25913, Korea; [email protected] 2 KIIT (Kangwon Institute of Inclusive Technology), Kangwon National University, 1 Gangwondaegil, Chuncheon 24341, Korea; [email protected] * Correspondence: [email protected] (C.P.); [email protected] (K.-K.Y.); Tel.: +82-33-570-6515 (C.P.); +82-33-250-6236 (K.-K.Y.) Received: 11 October 2019; Accepted: 19 December 2019; Published: 1 January 2020 Abstract: The compressive stress of concrete is used as a design variable for reinforced concrete structures in design standards. However, as the performance-based design is being used with increasing varieties and strengths of concrete and reinforcement bars, mechanical properties other than the compressive stress of concrete are sometimes used as major design variables. In particular, the evaluation of the mechanical properties of concrete is crucial when using fiber-reinforced concrete. Studies of high volume fractions in established compressive behavior prediction equations are insufficient compared to studies of conventional fiber-reinforced concrete. Furthermore, existing prediction equations for the mechanical properties of high-performance fiber-reinforced cementitious composite and high-strength concrete have limitations in terms of the strength and characteristics of contained fibers (diameter, length, volume fraction) even though the stress-strain relationship is determined by these factors. Therefore, this study developed a high-performance slurry-infiltrated fiber-reinforced cementitious composite that could prevent the fiber ball phenomenon, a disadvantage of conventional fiber-reinforced concrete, and maximize the fiber volume fraction. -
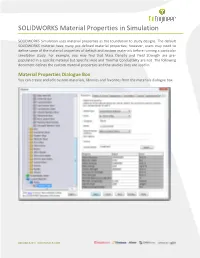
SOLIDWORKS Material Properties in Simulation
SOLIDWORKS Material Properties in Simulation SOLIDWORKS Simulation uses material properties as the foundation to study designs. The default SOLIDWORKS material have many pre-defined material properties; however, users may need to define some of the material properties of default and custom materials before running a particular simulation study. For example, you may find that Mass Density and Yield Strength are pre- populated in a specific material but Specific Heat and Thermal Conductivity are not. The following document defines the custom material properties and the studies they are used in. Material Properties Dialogue Box You can create and edit custom materials, libraries and favorites from the materials dialogue box. 888.688.3234 | GOENGINEER.COM Elastic Modulus The Elastic Modulus (Young’s Modulus) is the ratio of stress versus strain in the X, Y or Z directions. Elastic Moduli are used in static, nonlinear, frequency, dynamic, and buckling analyses. Poisson's Ratio Poisson’s Ratio is the negative ratio between transverse and axial strain. Poisson’s ratios are dimensionless quantities. For isotropic materials, the Poisson’s ratios in all planes are equal. Poisson ratios are used in static, nonlinear, frequency, dynamic and buckling Shear Modulus Shear Modulus (Modulus of Rigidity) is the ratio of shear stress to shear strain Shear Moduli are used in static, nonlinear, frequency, dynamic and buckling analyses. Mass Density Mass Density is used in static, nonlinear, frequency, dynamic, buckling, and thermal analyses. Static and buckling analyses use this property only if you define body forces (gravity and/or centrifugal). Tensile Strength Tensile Strength is the maximum that a material can withstand before stretching or breaking. -

The Strength of Concrete
The Strength of Chapter Concrete 3 3.1 The Importance of Strength 3.2 Strength Level Required KINDS OF STRENGTH 3.3 Compressive Strength 3.4 Flexural Strength 3.5 Tensile Strength 3.6 Shear, Torsion and Combined Stresses 3.7 Relationship of Test Strength to the Structure MEASUREMENT OF STRENGTH 3.8 Job-Molded Specimens 3.9 Te s t i n g o f H a r d e n e d C o n c r e t e FACTORS AFFECTING STRENGTH 3.10 General Comments 3.11 Causes of Strength Variations –Cement – Aggregates – Mix Proportioning – Making and Handling the Concrete – Temperature and Curing 3.12 Apparent Low Strength 3.13 Accelerated Strength Development – High-Early-Strength Cement –Admixtures – Retention of Heat of Hydration – High-Temperature Curing – Rapid-Setting Cements 3.14 Slow Strength Development HIGH-STRENGTH CONCRETE (HSC) 3.15 Selection of Materials and Mix 3.16 Handling and Quality Control EARLY MEASUREMENT OF STRENGTH EXPOSURE TO HIGH TEMPERATURE 3.17 Long-Time Exposure 3.18 Fire-Damaged Concrete 3 The Strength of Concrete The quality of concrete is judged largely on the strength of that concrete. Equipment and methods are continually being modernized, testing methods are improved, and means of analyzing and interpreting test data are becoming more sophisticated. Prior to the 2008 edition of the ACI 318 Standard, we relied almost exclusively on the strength of 6-by-12-inch cylinders, made on the jobsite and tested in compression at 28 days age for evaluation and acceptance of concrete. The use of 4-by-8-inch cylinders for strength evaluation was first addressed in ACI 318-08. -

Raplee Ridge Monocline and Thrust Fault Imaged Using Inverse Boundary Element Modeling and ALSM Data
Journal of Structural Geology 32 (2010) 45–58 Contents lists available at ScienceDirect Journal of Structural Geology journal homepage: www.elsevier.com/locate/jsg Structural geometry of Raplee Ridge monocline and thrust fault imaged using inverse Boundary Element Modeling and ALSM data G.E. Hilley*, I. Mynatt, D.D. Pollard Department of Geological and Environmental Sciences, Stanford University, Stanford, CA 94305-2115, USA article info abstract Article history: We model the Raplee Ridge monocline in southwest Utah, where Airborne Laser Swath Mapping (ALSM) Received 16 September 2008 topographic data define the geometry of exposed marker layers within this fold. The spatial extent of five Received in revised form surfaces were mapped using the ALSM data, elevations were extracted from the topography, and points 30 April 2009 on these surfaces were used to infer the underlying fault geometry and remote strain conditions. First, Accepted 29 June 2009 we compare elevations extracted from the ALSM data to the publicly available National Elevation Dataset Available online 8 July 2009 10-m DEM (Digital Elevation Model; NED-10) and 30-m DEM (NED-30). While the spatial resolution of the NED datasets was too coarse to locate the surfaces accurately, the elevations extracted at points Keywords: w Monocline spaced 50 m apart from each mapped surface yield similar values to the ALSM data. Next, we used Boundary element model a Boundary Element Model (BEM) to infer the geometry of the underlying fault and the remote strain Airborne laser swath mapping tensor that is most consistent with the deformation recorded by strata exposed within the fold. -

Dips Tutorial.Pdf
Dips Plotting, Analysis and Presentation of Structural Data Using Spherical Projection Techniques User’s Guide 1989 - 2002 Rocscience Inc. Table of Contents i Table of Contents Introduction 1 About this Manual ....................................................................................... 1 Quick Tour of Dips 3 EXAMPLE.DIP File....................................................................................... 3 Pole Plot....................................................................................................... 5 Convention .............................................................................................. 6 Legend..................................................................................................... 6 Scatter Plot .................................................................................................. 7 Contour Plot ................................................................................................ 8 Weighted Contour Plot............................................................................. 9 Contour Options ...................................................................................... 9 Stereonet Options.................................................................................. 10 Rosette Plot ............................................................................................... 11 Rosette Applications.............................................................................. 12 Weighted Rosette Plot.......................................................................... -

Comparison of Tensile and Compressive Properties of Carbon/Glass Interlayer and Intralayer Hybrid Composites
materials Article Comparison of Tensile and Compressive Properties of Carbon/Glass Interlayer and Intralayer Hybrid Composites Weili Wu 1 ID , Qingtao Wang 1 ID and Wei Li 1,2,3,* ID 1 College of Textiles, Donghua University, No. 2999, Northern Renmin Rd., Songjiang District, Shanghai 201620, China; [email protected] (W.W.); [email protected] (Q.W.) 2 Key Lab of Textile Science & Technology, Ministry of Education, Shanghai 201620, China 3 Center for Civil Aviation Composites, Shanghai 201620, China * Correspondence: [email protected]; Tel.: +86-137-6402-2421 Received: 27 May 2018; Accepted: 25 June 2018; Published: 28 June 2018 Abstract: Tensile and compressive properties of interlayer and intralayer hybrid composites were investigated in this paper. The tensile modulus and compression modulus of interlayer and intralayer hybrid composites are the same under the same mixed ratio, the tensile strength is much superior to the compression strength, and while the tensile modulus and strength increase along with the carbon fiber content, the compression values change slightly. The influence of stacking structures on the tensile and compressive strengths is opposite to the ratio of T/C (tensile/compression) strength for interlayer hybrid composites, and while the tensile and compression strengths with glass fiber sandwiching carbon fiber can reach the maximum value, the ratio of T/C strength is minimum. For structures with carbon fiber sandwiching glass fiber, or with asymmetric structures, the tensile and compressive strengths are at a low value. For intralayer hybrid structures, while the carbon/glass (C/G) dispersion degree is high, the tensile and compression strengths are low. -

The Mechanical Properties of Saline Ice Under Uniaxial Compression Gary A
IGS lntern•tional Symp<>Sium Ofl Applied (a! and Snow Re:sevd!:, Rovaniemi. Flnland; 18·23 April 1993 The Mechanical Properties of Saline Ice Under Uniaxial Compression Gary A. Kuehn and Briand M. Schulson Ice Research Laboratory Thayer School of Engineering, Dartmouth College 8000 Cummings Hall, Hanover, NH 03755-8000 603-646-3763, 603-646-3828 : FAX [email protected] : internet [email protected] : internet Annals of Glaciology ABSTRACT (in press, June 1993) Understanding the mechanical properties of saline ice is important for engineering design as well as for operations in polar regions. In order to gain understanding of the basic mechanisms of deformation and fracture, laboratory-grown columnar saline ice, representative of first-year sea ice, was tested in uniaxial comptession under a variety of conditions of strain rate oo-7 to 10-1 per second), temperature (-40', -20', -10· and .5·c) and orientation (loading vertically or horizontally: i.e. parallel or perpendicular to the growth direction). The range of strain rate spanned the ductile-to-brittle transition for every combination of temperature and specimen orientation. The results of over 250 tests are reported. Mechanical properties, failure mode and ice structure are analyzed with respect to the testing conditions. The results show that strength is dependent upon the ice structure, orientation, strain rate and temperature. During loading in the ductile regime the structure is altered (e.g. by recrystallization), whereas in the brittle regime the majority of the structural change is through cracking. The results are compared to results from the literature on both natural sea ice and laboratory-grown saline ice. -

Fracture Cleavage'' in the Duluth Complex, Northeastern Minnesota
Downloaded from gsabulletin.gsapubs.org on August 9, 2013 Geological Society of America Bulletin ''Fracture cleavage'' in the Duluth Complex, northeastern Minnesota M. E. FOSTER and P. J. HUDLESTON Geological Society of America Bulletin 1986;97, no. 1;85-96 doi: 10.1130/0016-7606(1986)97<85:FCITDC>2.0.CO;2 Email alerting services click www.gsapubs.org/cgi/alerts to receive free e-mail alerts when new articles cite this article Subscribe click www.gsapubs.org/subscriptions/ to subscribe to Geological Society of America Bulletin Permission request click http://www.geosociety.org/pubs/copyrt.htm#gsa to contact GSA Copyright not claimed on content prepared wholly by U.S. government employees within scope of their employment. Individual scientists are hereby granted permission, without fees or further requests to GSA, to use a single figure, a single table, and/or a brief paragraph of text in subsequent works and to make unlimited copies of items in GSA's journals for noncommercial use in classrooms to further education and science. This file may not be posted to any Web site, but authors may post the abstracts only of their articles on their own or their organization's Web site providing the posting includes a reference to the article's full citation. GSA provides this and other forums for the presentation of diverse opinions and positions by scientists worldwide, regardless of their race, citizenship, gender, religion, or political viewpoint. Opinions presented in this publication do not reflect official positions of the Society. Notes Geological Society of America Downloaded from gsabulletin.gsapubs.org on August 9, 2013 "Fracture cleavage" in the Duluth Complex, northeastern Minnesota M. -

ROCK STRENGTH (Text Ch. 3)
Lecture 9 – Introduction to Rock Strength David Hart University of Wisconsin ecow.engr.wisc.edu/cgi- bin/get/gle/474/hartdavid/notes/lectu re9strengthintro.ppt - ROCK STRENGTH • Shear fracture is the dominant mode of failure for rocks under all but the lowest confining stress. Extension Compression Paterson, Experimental Rock Deformation – The Brittle Field Example from Goodman, Intro to Rock Mechanics ROCK STRENGTH • The peak stress is the strength of the rock. – It may fail catastrophically if the load frame is “soft”. Example below is for a “stiff” frame. • The compressive strength of rock is a function of the confining pressure. • As the confining pressure increases so does the strength. Goodman, Intro to Rock Mechanics ROCK STRENGTH • The variation of peak stress σ1, peak (at which failure occurs) with the confining pressure (for which σ2 = σ3 ) is referred to as the rock CRITERION OF FAILURE. • The simplest and the best known failure criterion of failure is the MOHR-COULOMB (M-C) criterion: the linear approximation of the variation of peak stress σ1, peak with the confining pressure. MOHR-COULOMB Criterion of Failure • It has been established that rock fails in σ1,p compression by shearing along a ‘failure’ plane oriented at an angle θ with respect to σ1 that is specific for a particular rock. Rock • The M-C linear strength criterion cylinder σ =σ implies that θ stays the same regardless 2 3 of the confining pressure applied. τ 2θ 2θ 2θ σ 0 σ2=σ3 1,p σ MOHR-COULOMB Criterion τ = Si + σ tanφ τ cr φ A D 2θ Sι φ 90o C 0 σ2=σ3 Co B σ1,p σ MOHR-COULOMB Criterion in terms of shear and normal stress on the plane of failure τ cr = Si + σ tanφ where Iτlcr is the shear strength, Si (cohesion) is the intercept with the τ axis of the linear envelope, and φ ('angle of friction') is the slope angle of the linear envelope of failure. -

A New Expansion Material Used for Roof-Contacted Filling Based on Smelting Slag
www.nature.com/scientificreports OPEN A new expansion material used for roof‑contacted flling based on smelting slag Hua Na1, Guocheng Lv1*, Lijuan Wang1, Libing Liao1, Dan Zhang2, Lijie Guo2* & Wenchen Li2 The improper handling of smelting slag will seriously pollute the environment, and the unflled roof of the goaf of the mine will threaten the safety of the mine. Expansion materials have attracted more and more attention because of their excellent properties. In this paper, copper‑nickel smelting slag that has some active ingredients of gelling is used instead of traditional aggregate and some part of cement in order to reduce its pollution to the environment and its costs. For safety reasons, hydrogen peroxide was chosen as the foaming agent. Sodium silicate and hexadecyl trimethyl ammonium bromide (CTAB) are used as additives. Our results showed that after 28 days of curing, the material has better mechanical properties and the early compressive strength of the material was enhanced by sodium silicate. The efciency of foaming was improved by CTAB. It also proves that copper–nickel smelting slag can be used in expansion material. At the same time, the utilization rate of the copper– nickel smelting slag of this formula can reach 70%, reduce its pollution to the environment. Mineral resources are one of the most critical parts of the development of society. Filling mining technology is a mining technology that uses flling materials to fll underground goaf. Tere are many kinds of flling materi- als, such as barren rocks, slags, tailings, cementitious material and cementitious material prepared with cement and the solid waste mentioned above in the land mines 1–8. -

Glossary of Transportation Construction Quality Assurance Terms
TRANSPORTATION RESEARCH Number E-C235 August 2018 Glossary of Transportation Construction Quality Assurance Terms Seventh Edition TRANSPORTATION RESEARCH BOARD 2018 EXECUTIVE COMMITTEE OFFICERS Chair: Katherine F. Turnbull, Executive Associate Director and Research Scientist, Texas A&M Transportation Institute, College Station Vice Chair: Victoria A. Arroyo, Executive Director, Georgetown Climate Center; Assistant Dean, Centers and Institutes; and Professor and Director, Environmental Law Program, Georgetown University Law Center, Washington, D.C. Division Chair for NRC Oversight: Susan Hanson, Distinguished University Professor Emerita, School of Geography, Clark University, Worcester, Massachusetts Executive Director: Neil J. Pedersen, Transportation Research Board TRANSPORTATION RESEARCH BOARD 2017–2018 TECHNICAL ACTIVITIES COUNCIL Chair: Hyun-A C. Park, President, Spy Pond Partners, LLC, Arlington, Massachusetts Technical Activities Director: Ann M. Brach, Transportation Research Board David Ballard, Senior Economist, Gellman Research Associates, Inc., Jenkintown, Pennsylvania, Aviation Group Chair Coco Briseno, Deputy Director, Planning and Modal Programs, California Department of Transportation, Sacramento, State DOT Representative Anne Goodchild, Associate Professor, University of Washington, Seattle, Freight Systems Group Chair George Grimes, CEO Advisor, Patriot Rail Company, Denver, Colorado, Rail Group Chair David Harkey, Director, Highway Safety Research Center, University of North Carolina, Chapel Hill, Safety and Systems