DOCSLIB.ORG

System F with Type Equality Coercions Including Post-Publication Appendix

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
System F with Type Equality Coercions Including Post-Publication Appendix System F with Type Equality Coercions Including post-publication Appendix January 19, 2011 Martin Sulzmann Manuel M. T. Chakravarty Simon Peyton Jones Kevin Donnelly School of Computing Computer Science & Engineering Microsoft Research Ltd National University of Singapore University of New South Wales Cambridge, England [email protected] [email protected] fsimonpj,[email protected] Abstract nesses to justify explicit type-cast operations. Like types, coercions are erased before running the program, so they are guaranteed to We introduce System FC, which extends System F with support for non-syntactic type equality. There are two main extensions: (i) have no run-time cost. explicit witnesses for type equalities, and (ii) open, non-parametric This single mechanism allows a very direct encoding of associ- type functions, given meaning by top-level equality axioms. Unlike ated types and GADTs, and allows us to deal with some exotic System F, FC is expressive enough to serve as a target for several functional-dependency programs that GHC currently rejects on the different source-language features, including Haskell’s newtype, grounds that they have no System-F translation (x2). Our specific generalised algebraic data types, associated types, functional de- contributions are these: pendencies, and perhaps more besides. • NOTE: this version has a substantial Appendix, written subse- We give a formal description of System FC, our new intermedi- quent to the publication of the paper, giving a simplified ver- ate language, including its type system, operational semantics, sion of System FC. This version is much closer to the one used soundness result, and erasure properties (x3). There are two dis- in GHC. tinct extensions. The first, explicit equality witnesses, gives a system equivalent in power to System F + GADTs (x3.2); the Categories and Subject Descriptors D.3.1 [Programming Lan- second introduces non-parametric type functions, and adds sub- guages]: Formal Definitions and Theory—Semantics; F.3.3 [Log- stantial new power, well beyond System F + GADTs (x3.3). ics and Meanings of Programs]: Studies of Program Constructs— Type structure • A distinctive property of FC’s type functions is that they are open (x3.4). Here we use “open” in the same sense that Haskell General Terms Languages, Theory type classes are open: just as a newly defined type can be Keywords Typed intermediate language, advanced type features made an instance of an existing class, so in FC we can extend an existing type function with a case for the new type. This 1. Introduction property is crucial to the translation of associated types. The polymorphic lambda calculus, System F, is popular as a highly- • The system is very general, and its soundness requires that the expressive typed intermediate language in compilers for functional axioms stated as part of the program text are consistent (x3.5). languages. However, language designers have begun to experiment That is why we call the system FC(X): the “X” indicates that with a variety of type systems that are difficult or impossible to it is parametrised over a decision procedure for checking con- translate into System F, such as functional dependencies [21], gen- sistency, rather than baking in a particular decision procedure. eralised algebraic data types (GADTs) [44, 31], and associated (We often omit the “(X)” for brevity.) Conditions identified in types [6, 5]. For example, when we added GADTs to GHC, we earlier work on GADTs, associated types, and functional de- extended GHC’s intermediate language with GADTs as well, even pendencies, already define such decision procedures. though GADTs are arguably an over-sophisticated addition to a • A major goal is that FC should be a practical compiler inter- typed intermediate language. But when it came to associated types, mediate language. We have paid particular attention to ensuring even with this richer intermediate language, the translation became that FC programs are robust to program transformation (x3.8). extremely clumsy or in places impossible. • It must obviously be possible to translate the source language F In this paper we resolve this problem by presenting System C(X), into the intermediate language; but it is also highly desirable more foundational more powerful a super-set of F that is both and that it be straightforward. We demonstrate that F has this ad hoc C than adding extensions to System F such as GADTs or as- property, by sketching a type-preserving translation of two F sociated types. C(X) uses explicit type-equality coercions as wit- source language idioms, namely GADTs (Section 4) and as- sociated types (Section 5). The latter, and the corresponding translation for functional dependencies, are more general than all previous type-preserving translations for these features. System FC has no new foundational content: rather, it is an intrigu- ing and practically-useful application of techniques that have been Abridged version appears in The Third ACM SIGPLAN Workshop well studied in the type-theory community. Several other calculi on Types in Language Design and Implementation (TLDI’07), Jan- exist that might in principle be used for our purpose, but they gen- uary 16, 2007, Nice, France, ACM Press. erally do not handle open type functions, are less robust to trans- 1 2011/1/19 formation, and are significantly more complicated. We defer a com- representing GADTs by ordinary algebraic data types encapsulat- parison with related work until x6. ing such type equality coercions. To substantiate our claim that FC is practical, we have implemented Specifically, we translate the GADT Exp to an ordinary algebraic it in GHC, a state-of-the-art compiler for Haskell, including both data type, where each variant is parametrised by a coercion: GADTs and associated (data) types. This is not just a prototype; data Exp : ? ! ? where FC now is GHC’s intermediate language. Zero : 8a: (a ∼Int) ) Exp a FC does not strive to do everything; rather we hope that it strikes Succ : 8a: (a ∼Int) ) Exp Int ! Exp a an elegant balance between expressiveness and complexity. While Pair : 8abc: (a ∼(b; c)) ) Exp b ! Exp c ! Exp a our motivating examples were GADTs and associated types, we believe that FC may have much wider application as a typed target So far, this is quite standard; indeed, several authors present for sophisticated HOT (higher-order typed) source languages. GADTs in the source language using a syntax involving explicit equality constraints, similar to that above [44, 10]. However, for us 2. The key ideas the equality constraints are extra type arguments to the constructor, which must be given when the constructor is applied, and which pure No compiler uses System F as an intermediate language, are brought into scope by pattern matching. The “)” is syntac- because some source-language constructs can only be desugared tic sugar, and we sloppily omitted the kind of the quantified type into pure System F by very heavy encodings. A good example is variables, so the type of Zero is really this: the algebraic data types of Haskell or ML, which are made more complicated in Haskell because algebraic data types can capture Zero : 8 a: ?: 8(co:a ∼Int): Exp a existential type variables. To avoid heavy encoding, most compilers invariably extend System F by adding algebraic data types, data Here a ranges over types, of kind ?, while co ranges over coercions, constructors, and case expressions. We will use FA to describe of kind a ∼Int. An important property of our approach is that System F extended in this way, where the data constructors are coercions are types, and hence, equalities τ1 ∼τ2 are kinds. An allowed to have existential components [24], type variables can be equality kind τ1 ∼τ2 categorises all coercion types that witness the of higher kind, and type constructor applications can be partial. interchangeability of the two types τ1 and τ2. So, our slogan is Over the last few years, source languages (notably Haskell) have propositions as kinds, and proofs as (coercion) types. started to explore language features that embody non-syntactic or Coercion types may be formed from a set of elementary coer- definitional type equality. These features include functional depen- cions that correspond to the rules of equational logic; for example, dencies [16], generalised algebraic data types (GADTs) [44, 37], Int :(Int ∼Int) is an instance of the reflexivity of equality and and associated types [6, 5]. All three are difficult or impossible to sym co :(Int ∼a), with co :(a ∼Int), is an instance of symme- translate into System F — and yet the alternative of simply ex- try. A call of the constructor Zero must be given a type (to instan- tending System F by adding functional dependencies, GADTs, and tiate a) and a coercion (to instantiate co), thus for example: associated types, seems wildly unattractive. Where would one stop? Zero Int Int : Exp Int In the rest of this section we informally present System FC, an extension of System F that resolves the dilemma. We show how it As indicated above, regular types like Int, when interpreted as can serve as a target for each of the three examples. The formal coercions, witness reflexivity. x details are presented in 3. Throughout we use typewriter font Just like value arguments, the coercions passed to a constructor italics F for source-code, and for C. when it is built are made available again by pattern matching. Here, 2.1 GADTs then, is the code of eval in FC: Consider the following simple type-safe evaluator, often used as the eval = Λa: ? .λe:Exp a: poster child of GADTs, written in the GADT extension of Haskell case e of supported by GHC: Zero (co:a ∼Int) ! data Exp a where 0 I sym co Succ (co:a ∼Int)(e0:Exp Int) ! Zero :: Exp Int 0 Succ :: Exp Int -> Exp Int (eval Int e + 1) I sym co Pair :: Exp b -> Exp c -> Exp (b, c) Pair (b:?)(c:?)(co:a ∼(b; c)) (e1:Exp b)(e2:Exp c) ! eval :: Exp a -> a (eval b e1; eval c e2) I sym co eval Zero = 0 The form Λa: ?:e abstracts over types, as usual.
Load more

Recommended publications
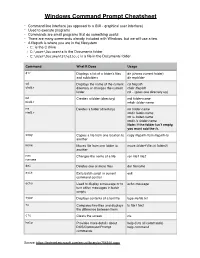
  • Windows Command Prompt Cheatsheet
    Windows Command Prompt Cheatsheet - Command line interface (as opposed to a GUI - graphical user interface) - Used to execute programs - Commands are small programs that do something useful - There are many commands already included with Windows, but we will use a few. - A filepath is where you are in the filesystem • C: is the C drive • C:\user\Documents is the Documents folder • C:\user\Documents\hello.c is a file in the Documents folder Command What it Does Usage dir Displays a list of a folder’s files dir (shows current folder) and subfolders dir myfolder cd Displays the name of the current cd filepath chdir directory or changes the current chdir filepath folder. cd .. (goes one directory up) md Creates a folder (directory) md folder-name mkdir mkdir folder-name rm Deletes a folder (directory) rm folder-name rmdir rmdir folder-name rm /s folder-name rmdir /s folder-name Note: if the folder isn’t empty, you must add the /s. copy Copies a file from one location to copy filepath-from filepath-to another move Moves file from one folder to move folder1\file.txt folder2\ another ren Changes the name of a file ren file1 file2 rename del Deletes one or more files del filename exit Exits batch script or current exit command control echo Used to display a message or to echo message turn off/on messages in batch scripts type Displays contents of a text file type myfile.txt fc Compares two files and displays fc file1 file2 the difference between them cls Clears the screen cls help Provides more details about help (lists all commands) DOS/Command Prompt help command commands Source: https://technet.microsoft.com/en-us/library/cc754340.aspx.
    [Show full text]
  • Proving Termination of Evaluation for System F with Control Operators
    Proving termination of evaluation for System F with control operators Małgorzata Biernacka Dariusz Biernacki Sergue¨ıLenglet Institute of Computer Science Institute of Computer Science LORIA University of Wrocław University of Wrocław Universit´ede Lorraine [email protected] [email protected] [email protected] Marek Materzok Institute of Computer Science University of Wrocław [email protected] We present new proofs of termination of evaluation in reduction semantics (i.e., a small-step opera- tional semantics with explicit representation of evaluation contexts) for System F with control oper- ators. We introduce a modified version of Girard’s proof method based on reducibility candidates, where the reducibility predicates are defined on values and on evaluation contexts as prescribed by the reduction semantics format. We address both abortive control operators (callcc) and delimited- control operators (shift and reset) for which we introduce novel polymorphic type systems, and we consider both the call-by-value and call-by-name evaluation strategies. 1 Introduction Termination of reductions is one of the crucial properties of typed λ-calculi. When considering a λ- calculus as a deterministic programming language, one is usually interested in termination of reductions according to a given evaluation strategy, such as call by value or call by name, rather than in more general normalization properties. A convenient format to specify such strategies is reduction semantics, i.e., a form of operational semantics with explicit representation of evaluation (reduction) contexts [14], where the evaluation contexts represent continuations [10]. Reduction semantics is particularly convenient for expressing non-local control effects and has been most successfully used to express the semantics of control operators such as callcc [14], or shift and reset [5].
    [Show full text]
  • Creating Rpms Guide
    CREATING RPMS (Student version) v1.0 Featuring 36 pages of lecture and a 48 page lab exercise This docu m e n t serves two purpose s: 1. Representative sample to allow evaluation of our courseware manuals 2. Make available high quality RPM documentation to Linux administrators A bout this m aterial : The blue background you see simulates the custom paper that all Guru Labs course w are is printed on. This student version does not contain the instructor notes and teaching tips present in the instructor version. For more information on all the features of our unique layout, see: http://ww w . g urulabs.co m /courseware/course w are_layout.php For more freely available Guru Labs content (and the latest version of this file), see: http://www.gurulabs.co m/goodies/ This sample validated on: Red Hat Enterprise Linux 4 & Fedora Core v3 SUSE Linux Enterprise Server 9 & SUSE Linux Professional 9.2 About Guru Labs: Guru Labs is a Linux training company started in 199 9 by Linux experts to produce the best Linux training and course w are available. For a complete list, visit our website at: http://www.gurulabs.co m/ This work is copyrighted Guru Labs, L.C. 2005 and is licensed under the Creative Common s Attribution- NonCom mer cial- NoDerivs License. To view a copy of this license, visit http://creativecom m o n s.org/licenses/by- nc- nd/2.0/ or send a letter to Creative Commons, 559 Nathan Abbott Way, Stanford, California 943 0 5, USA. Guru Labs 801 N 500 W Ste 202 Bountiful, UT 84010 Ph: 801-298-5227 WWW.GURULABS.COM Objectives: • Understand
    [Show full text]
  • The Frege Programming Language ( Draft)
    The Frege Programming Language (Draft) by Ingo Wechsung last changed May 14, 2014 3.21.285 Abstract This document describes the functional programming language Frege and its implemen- tation for the Java virtual machine. Commonplace features of Frege are type inference, lazy evaluation, modularization and separate compile-ability, algebraic data types and type classes, pattern matching and list comprehension. Distinctive features are, first, that the type system supports higher ranked polymorphic types, and, second, that Frege code is compiled to Java. This allows for maximal interoperability with existing Java software. Any Java class may be used as an abstract data type, Java functions and methods may be called from Frege functions and vice versa. Despite this interoperability feature Frege is a pure functional language as long as impure Java functions are declared accordingly. What is or who was Frege? Friedrich Ludwig Gottlob Frege was a German mathematician, who, in the second half of the 19th century tried to establish the foundation of mathematics in pure logic. Al- though this attempt failed in the very moment when he was about to publish his book Grundgesetze der Arithmetik, he is nevertheless recognized as the father of modern logic among philosophers and mathematicians. In his essay Funktion und Begriff [1] Frege introduces a function that takes another function as argument and remarks: Eine solche Funktion ist offenbar grundverschieden von den bisher betrachteten; denn als ihr Argument kann nur eine Funktion auftreten. Wie nun Funktionen von Gegenst¨andengrundverschieden sind, so sind auch Funktionen, deren Argu- mente Funktionen sind und sein m¨ussen,grundverschieden von Funktionen, deren Argumente Gegenst¨andesind und nichts anderes sein k¨onnen.
    [Show full text]
  • Lecture Notes on Types for Part II of the Computer Science Tripos
    Q Lecture Notes on Types for Part II of the Computer Science Tripos Prof. Andrew M. Pitts University of Cambridge Computer Laboratory c 2016 A. M. Pitts Contents Learning Guide i 1 Introduction 1 2 ML Polymorphism 6 2.1 Mini-ML type system . 6 2.2 Examples of type inference, by hand . 14 2.3 Principal type schemes . 16 2.4 A type inference algorithm . 18 3 Polymorphic Reference Types 25 3.1 The problem . 25 3.2 Restoring type soundness . 30 4 Polymorphic Lambda Calculus 33 4.1 From type schemes to polymorphic types . 33 4.2 The Polymorphic Lambda Calculus (PLC) type system . 37 4.3 PLC type inference . 42 4.4 Datatypes in PLC . 43 4.5 Existential types . 50 5 Dependent Types 53 5.1 Dependent functions . 53 5.2 Pure Type Systems . 57 5.3 System Fw .............................................. 63 6 Propositions as Types 67 6.1 Intuitionistic logics . 67 6.2 Curry-Howard correspondence . 69 6.3 Calculus of Constructions, lC ................................... 73 6.4 Inductive types . 76 7 Further Topics 81 References 84 Learning Guide These notes and slides are designed to accompany 12 lectures on type systems for Part II of the Cambridge University Computer Science Tripos. The course builds on the techniques intro- duced in the Part IB course on Semantics of Programming Languages for specifying type systems for programming languages and reasoning about their properties. The emphasis here is on type systems for functional languages and their connection to constructive logic. We pay par- ticular attention to the notion of parametric polymorphism (also known as generics), both because it has proven useful in practice and because its theory is quite subtle.
    [Show full text]
  • The System F of Variable Types, Fifteen Years Later
    Theoretical Computer Science 45 (1986) 159-192 159 North-Holland THE SYSTEM F OF VARIABLE TYPES, FIFTEEN YEARS LATER Jean-Yves GIRARD Equipe de Logique Mathdmatique, UA 753 du CNRS, 75251 Paris Cedex 05, France Communicated by M. Nivat Received December 1985 Revised March 1986 Abstract. The semantic study of system F stumbles on the problem of variable types for which there was no convincing interpretation; we develop here a semantics based on the category-theoretic idea of direct limit, so that the behaviour of a variable type on any domain is determined by its behaviour on finite ones, thus getting rid of the circularity of variable types. To do so, one has first to simplify somehow the extant semantic ideas, replacing Scott domains by the simpler and more finitary qualitative domains. The interpretation obtained is extremely compact, as shown on simple examples. The paper also contains the definitions of a very small 'universal model' of lambda-calculus, and investigates the concept totality. Contents Introduction ................................... 159 1. Qualitative domains and A-structures ........................ 162 2. Semantics of variable types ............................ 168 3. The system F .................................. 174 3.1. The semantics of F: Discussion ........................ 177 3.2. Case of irrt ................................. 182 4. The intrinsic model of A-calculus .......................... 183 4.1. Discussion about t* ............................. 183 4.2. Final remarks ...............................
    [Show full text]
  • Lenovo Flex System FC3171 8 Gb SAN Switch Command Line Interface User’S Guide This Document Explains How to Manage the Switch Using the CLI
    Flex System FC3171 8 Gb SAN Switch Command Line Interface User’s Guide Flex System FC3171 8 Gb SAN Switch Command Line Interface User’s Guide Note: Before using this information and the product it supports, read the general information in “Notices” on page 391. First Edition, April 2015 © Copyright Lenovo 2015. LIMITED AND RESTRICTED RIGHTS NOTICE: If data or software is delivered pursuant a General Services Administration “GSA” contract, use, reproduction, or disclosure is subject to restrictions set forth in Contract No. GS-35F-05925. Contents Chapter 1. Lenovo Flex System FC3171 8 Gb SAN Switch . 1 Related documentation . 1 Notices and statements in this document . 3 Chapter 2. Command line interface usage . 5 Logging in to the switch . 6 Opening and closing an Admin session . 7 Entering commands. 7 Getting help . 7 Setting page breaks . 8 Creating a support file. 9 Downloading and uploading files. 10 Chapter 3. User account configuration . 13 Displaying user account information . 14 Creating user accounts . 15 Modifying user accounts and passwords. 15 Chapter 4. Network and fabric configuration . 17 Displaying the Ethernet network configuration . 17 Displaying name server information . 18 Configuring the Ethernet port . 19 IPv4 configuration . 19 IPv6 configuration . 20 DNS server configuration . 21 Verifying a switch in the network . 22 Verifying and tracing Fibre Channel connections . 22 Managing IP security. 23 IP security concepts . 24 Legacy and Strict security . 24 Security policies and associations . 24 IKE peers and policies . 25 Public key infrastructure . 25 Displaying IP security information . 25 Policy and association information . 25 IKE peer and policy information . 26 Public key infrastructure information .
    [Show full text]
  • An Introduction to Logical Relations Proving Program Properties Using Logical Relations
    An Introduction to Logical Relations Proving Program Properties Using Logical Relations Lau Skorstengaard [email protected] Contents 1 Introduction 2 1.1 Simply Typed Lambda Calculus (STLC) . .2 1.2 Logical Relations . .3 1.3 Categories of Logical Relations . .5 2 Normalization of the Simply Typed Lambda Calculus 5 2.1 Strong Normalization of STLC . .5 2.2 Exercises . 10 3 Type Safety for STLC 11 3.1 Type safety - the classical treatment . 11 3.2 Type safety - using logical predicate . 12 3.3 Exercises . 15 4 Universal Types and Relational Substitutions 15 4.1 System F (STLC with universal types) . 16 4.2 Contextual Equivalence . 19 4.3 A Logical Relation for System F . 20 4.4 Exercises . 28 5 Existential types 29 6 Recursive Types and Step Indexing 34 6.1 A motivating introduction to recursive types . 34 6.2 Simply typed lambda calculus extended with µ ............ 36 6.3 Step-indexing, logical relations for recursive types . 37 6.4 Exercises . 41 1 1 Introduction The term logical relations stems from Gordon Plotkin’s memorandum Lambda- definability and logical relations written in 1973. However, the spirit of the proof method can be traced back to Wiliam W. Tait who used it to show strong nor- malization of System T in 1967. Names are a curious thing. When I say “chair”, you immediately get a picture of a chair in your head. If I say “table”, then you picture a table. The reason you do this is because we denote a chair by “chair” and a table by “table”, but we might as well have said “giraffe” for chair and “Buddha” for table.
    [Show full text]
  • PS TEXT EDIT Reference Manual Is Designed to Give You a Complete Is About Overview of TEDIT
    Information Management Technology Library PS TEXT EDIT™ Reference Manual Abstract This manual describes PS TEXT EDIT, a multi-screen block mode text editor. It provides a complete overview of the product and instructions for using each command. Part Number 058059 Tandem Computers Incorporated Document History Edition Part Number Product Version OS Version Date First Edition 82550 A00 TEDIT B20 GUARDIAN 90 B20 October 1985 (Preliminary) Second Edition 82550 B00 TEDIT B30 GUARDIAN 90 B30 April 1986 Update 1 82242 TEDIT C00 GUARDIAN 90 C00 November 1987 Third Edition 058059 TEDIT C00 GUARDIAN 90 C00 July 1991 Note The second edition of this manual was reformatted in July 1991; no changes were made to the manual’s content at that time. New editions incorporate any updates issued since the previous edition. Copyright All rights reserved. No part of this document may be reproduced in any form, including photocopying or translation to another language, without the prior written consent of Tandem Computers Incorporated. Copyright 1991 Tandem Computers Incorporated. Contents What This Book Is About xvii Who Should Use This Book xvii How to Use This Book xvii Where to Go for More Information xix What’s New in This Update xx Section 1 Introduction to TEDIT What Is PS TEXT EDIT? 1-1 TEDIT Features 1-1 TEDIT Commands 1-2 Using TEDIT Commands 1-3 Terminals and TEDIT 1-3 Starting TEDIT 1-4 Section 2 TEDIT Topics Overview 2-1 Understanding Syntax 2-2 Note About the Examples in This Book 2-3 BALANCED-EXPRESSION 2-5 CHARACTER 2-9 058059 Tandem Computers
    [Show full text]
  • RL78/G23 Unique ID Read Driver Introduction Each RL78/G2x Chip Is Programmed with a Unique ID
    Application Note RL78/G23 Unique ID Read Driver Introduction Each RL78/G2x chip is programmed with a unique ID. The unique ID can be used to prevent unauthorized use of software IP and is useful for managing products individually. This application note presents unique ID usage examples and describes how to use the unique ID read driver. The driver reads the 16-byte unique ID and 9-byte product name stored as ASCII code in the extra area and writes them to a specified area. Target Device RL78/G23 When using this application note with other Renesas MCUs, careful evaluation is recommended after making modifications to comply with the alternate MCU. R20AN0615EJ0100 Rev.1.00 Page 1 of 14 Apr.13.21 RL78/G23 Unique ID Read Driver Contents 1. Overview .................................................................................................................................... 3 1.1 About This Application Note .................................................................................................................... 3 1.2 Confirmed Operation Environment .......................................................................................................... 3 2. About the Unique ID .................................................................................................................. 5 2.1 Unique ID Specifications ......................................................................................................................... 5 2.2 Unique ID Usage Examples ...................................................................................................................
    [Show full text]
  • Lightweight Linear Types in System F°
    University of Pennsylvania ScholarlyCommons Departmental Papers (CIS) Department of Computer & Information Science 1-23-2010 Lightweight linear types in System F° Karl Mazurak University of Pennsylvania Jianzhou Zhao University of Pennsylvania Stephan A. Zdancewic University of Pennsylvania, [email protected] Follow this and additional works at: https://repository.upenn.edu/cis_papers Part of the Computer Sciences Commons Recommended Citation Karl Mazurak, Jianzhou Zhao, and Stephan A. Zdancewic, "Lightweight linear types in System F°", . January 2010. Karl Mazurak, Jianzhou Zhao, and Steve Zdancewic. Lightweight linear types in System Fo. In ACM SIGPLAN International Workshop on Types in Languages Design and Implementation (TLDI), pages 77-88, 2010. doi>10.1145/1708016.1708027 © ACM, 2010. This is the author's version of the work. It is posted here by permission of ACM for your personal use. Not for redistribution. The definitive version was published in ACM SIGPLAN International Workshop on Types in Languages Design and Implementation, {(2010)} http://doi.acm.org/10.1145/1708016.1708027" Email [email protected] This paper is posted at ScholarlyCommons. https://repository.upenn.edu/cis_papers/591 For more information, please contact [email protected]. Lightweight linear types in System F° Abstract We present Fo, an extension of System F that uses kinds to distinguish between linear and unrestricted types, simplifying the use of linearity for general-purpose programming. We demonstrate through examples how Fo can elegantly express many useful protocols, and we prove that any protocol representable as a DFA can be encoded as an Fo type. We supply mechanized proofs of Fo's soundness and parametricity properties, along with a nonstandard operational semantics that formalizes common intuitions about linearity and aids in reasoning about protocols.
    [Show full text]
  • CS 6110 S18 Lecture 32 Dependent Types 1 Typing Lists with Lengths
    CS 6110 S18 Lecture 32 Dependent Types When we added kinding last time, part of the motivation was to complement the functions from types to terms that we had in System F with functions from types to types. Of course, all of these languages have plain functions from terms to terms. So it's natural to wonder what would happen if we added functions from values to types. The result is a language with \compile-time" types that can depend on \run-time" values. While this arrangement might seem paradoxical, it is a very powerful way to express the correctness of programs; and via the propositions-as-types principle, it also serves as the foundation for a modern crop of interactive theorem provers. The language feature is called dependent types (i.e., types depend on terms). Prominent dependently-typed languages include Coq, Nuprl, Agda, Lean, F*, and Idris. Some of these languages, like Coq and Nuprl, are more oriented toward proving things using propositions as types, and others, like F* and Idris, are more oriented toward writing \normal programs" with strong correctness guarantees. 1 Typing Lists with Lengths Dependent types can help avoid out-of-bounds errors by encoding the lengths of arrays as part of their type. Consider a plain recursive IList type that represents a list of any length. Using type operators, we might use a general type List that can be instantiated as List int, so its kind would be type ) type. But let's use a fixed element type for now. With dependent types, however, we can make IList a type constructor that takes a natural number as an argument, so IList n is a list of length n.
    [Show full text]