Lecture 5 - Choice, Demand
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Giffen Behaviour and Asymmetric Substitutability*
Tjalling C. Koopmans Research Institute Tjalling C. Koopmans Research Institute Utrecht School of Economics Utrecht University Janskerkhof 12 3512 BL Utrecht The Netherlands telephone +31 30 253 9800 fax +31 30 253 7373 website www.koopmansinstitute.uu.nl The Tjalling C. Koopmans Institute is the research institute and research school of Utrecht School of Economics. It was founded in 2003, and named after Professor Tjalling C. Koopmans, Dutch-born Nobel Prize laureate in economics of 1975. In the discussion papers series the Koopmans Institute publishes results of ongoing research for early dissemination of research results, and to enhance discussion with colleagues. Please send any comments and suggestions on the Koopmans institute, or this series to [email protected] ontwerp voorblad: WRIK Utrecht How to reach the authors Please direct all correspondence to the first author. Kris De Jaegher Utrecht University Utrecht School of Economics Janskerkhof 12 3512 BL Utrecht The Netherlands. E-mail: [email protected] This paper can be downloaded at: http:// www.uu.nl/rebo/economie/discussionpapers Utrecht School of Economics Tjalling C. Koopmans Research Institute Discussion Paper Series 10-16 Giffen Behaviour and Asymmetric * Substitutability Kris De Jaeghera aUtrecht School of Economics Utrecht University September 2010 Abstract Let a consumer consume two goods, and let good 1 be a Giffen good. Then a well- known necessary condition for such behaviour is that good 1 is an inferior good. This paper shows that an additional necessary for such behaviour is that good 1 is a gross substitute for good 2, and that good 2 is a gross complement to good 1 (strong asymmetric gross substitutability). -

1 Economics 100A: Microeconomic Analysis Fall 2001 Problem Set 4
Economics 100A: Microeconomic Analysis Fall 2001 Problem Set 4 (Due the week of September 24) Answers 1. An inferior good is defined as one of which an individual demands less when his or her income rises and more when his or her income falls. A normal good is defined as one of which an individual demands more when his or her income increases and less when his or her income falls. A luxury good is defined as one for which its demand increases by a greater proportion than income. A necessary is defined as one for which its demand increases by a lesser proportion than income. The same good can be both normal and inferior. For instance, a good can be normal up to some level of income beyond which it becomes inferior. Such a good would have a backward-bending Engel curve. 2. (a) Table 2. Percentage Allocation of Family Budget Income Groups A B C D E Food Prepared at Home 26.1 21.5 20.8 18.6 13.0 Food Away from Home 3.8 4.7 4.1 5.2 6.1 Housing 35.1 30.0 29.2 27.6 29.6 Clothing 6.7 9.0 9.8 11.2 12.3 Transportation 7.8 14.3 16.0 16.5 14.4 (b) All of them. (c) Food away from home, clothing and transportation. (d) Food prepared at home and housing. (e) The graph below depicts the Engel curve for food away from home (a luxury good). (f) The graph below depicts the Engel curve for food prepared at home (a necessity good). -

Impure Public Goods and the Comparative Statics of Environmentally Friendly Consumption
ARTICLE IN PRESS Journal of Environmental Economics and Management 49 (2005) 281–300 www.elsevier.com/locate/jeem Impure public goods and the comparative statics of environmentally friendly consumption Matthew J. Kotchenà Department of Economics, Williams College, Fernald House, Williamstown, MA 01267, USA Received 19 September 2003; received in revised form 4 March 2004; accepted 12 May 2004 Available online 5 August 2004 Abstract This paper develops an impure public good model to analyze the comparative statics of environmentally friendly consumption. ‘‘Green’’ products are treated as impure public goods that arise through joint production of a private characteristic and an environmental public characteristic. The model is distinct from existing impure public good models because of the way it considers the availability of substitutes. Specifically, the model accounts for the way that the jointly produced characteristics of a green product may be available separately as well—through a conventional-good substitute, direct donations to improve environmental quality, or both. The analysis provides a theoretical foundation for understanding how demand for green products and demand for environmental quality depend on market prices, green- production technologies, and ambient environmental quality. The comparative static results generate new insights into the important and sometimes counterintuitive relationship between demand for green products and demand for environmental quality. r 2004 Elsevier Inc. All rights reserved. Keywords: Impure public goods; Green products; Environmental quality 1. Introduction Consumers are often willing to pay for goods and services that are considered ‘‘environmentally friendly’’ (or ‘‘green’’), and markets designed to meet this demand are expanding. Market research ÃFax: +413-597-4045. -

Is Shopping at Walmart an Inferior Good? Evidence from 1997-2010
Is Shopping at Walmart an Inferior Good? Evidence from 1997-2010 Mike Allgrunn University of South Dakota Mandie Weinandt University of South Dakota We test the relative income elasticity of shopping at Walmart and Target using quarterly data from 1997- 2010. We seek to isolate the effects of income changes by controlling for price level, retail space, and measures of time. Our findings indicate Walmart’s income elasticity, while lower than Target’s, is positive, indicating shopping at both stores is normal rather than inferior. INTRODUCTION Walmart is often described as performing well during recessions. The common narrative is Walmart offers a low-price shopping experience consumers value more during a recession than when their incomes are higher (Bustillo and Zimmerman, 2008 and Zwaniecki, 2008). This seems to be a textbook example of what economists call an inferior good. A good or service is ‘inferior’ in the economic sense if consumers buy more when their incomes fall, other things equal. Put another way, a good or service is inferior if its income elasticity of demand is less than zero. This is different than simply analyzing financial performance during recessions. It would not be enough, for example, to note Walmart’s earnings rise when incomes fall, as earnings could rise for many reasons. An ideal test would hold prices and supply factors constant to isolate the effect of income on demand. In this paper we construct such a test to determine the income elasticity of demand for shopping at Walmart and close competitor, Target. LITERATURE REVIEW There are a number of studies which examine income elasticity of individual goods. -

1 Demand and Supply I. Demand Defined
Demand and Supply I. Demand Defined A. Demand is defined as follows: demand shows how much a consumer or consumers are willing and able to buy (known as quantity demanded) given the price, ceteris paribus. B. The law of Demand The law of demand simply acknowledges that price and QD are inversely related. That is, as price Price increases then QD decreases, ceteris paribus, and the reverse. Hence, the relationship is as shown in Graph 1. It is not too surprising to most of us that consumers, people like you and Demand I, buy less of a good, all else equal, as the good’s price increases and Quantity the reverse. That is because we Graph 1 observe ourselves acting in this manner when we make purchases. Although unsurprising, it tends to be more difficult for us to identify exactly why consumers respond by increasing their purchases of a good when its price falls. There exist two reasons: • Substitution effect When the price of a good falls, ceteris paribus, individuals tend to buy more of that good because the price has become less expensive relative to that good’s substitutes. A good is a substitute in consumption for another good if the goods fulfill the same basic purpose. Hence, when the price of apples falls, then people tend to buy more apples and fewer of apples’ substitutes, such as oranges and bananas. The reverse is true as well for a price increase of a good. • Income Effect When the price of a good falls, ceteris paribus, individuals tend to buy more of that good because they have more money. -

Lecture 3 - Consumer Demand
Economics 101 Lecture 3 - Consumer Demand 1 Intro First, a note on wealth and endowment. Varian generally uses wealth (m) instead of endowment. Ultimately, these two are equivalent. Given prices p, if we have endowment e, our wealth is simply w = p · e. Conversely, if we have wealth w, this is the same as have an endowment e given by w ei = P j pj so that p · e = w. Note that there are many other endowments that lead to wealth w. Last lecture we investigated how consumers make choices by maximizing their utility subject to the budget constraint. Given prices and endowment, we found what the consumer's optimal choice was. Now we'll formalize this Demand Function: For any prices and endowment, a demand function gives the bundle of goods x(p; e) optimally chosen by the consumer. Notice that give the relationship between endowment and wealth, it is equiv- alent to define demand simply as a function of prices and wealth. Sometimes, to avoid confusion I will add superscripts to denote which function I'm talking about. These functions are related by xe(p; e) = xw(p; p · e) We are free to do this because the only thing that determines the shape of the budget set is normalized prices and wealth. Changing the endowment while keeping wealth constant does not change the budget line. It only changes where the endowment lies on the budget line, which does not affect the optimal choice. 1 Also note that we assume throughout that x is a function, meaning that the is one and only one optimal choice. -

Introduction to Demand 1. Willy Wonka Helps Us to Understand the “Law of Demand.” As Prices Fall the Quantity Demanded of Go
Introduction to Demand 1. Willy Wonka helps us to understand the “Law of Demand.” As prices fall the quantity demanded of goods falls. Wonka can also help us understand the impact of changes in the price of related goods and income have on the demand curve. Use the meme’s below to identify what type of good Wonka is describing. Then use the meme generator at http://memegenerator.net/ to create your own memes for the law of demand, normal goods, inferior goods, complements, and substitutes. Also create a meme for the impact of a change in tastes/preferences and expecations. Type of good being described Meme Explanation (circle the correct answer) . Normal good If your income drops and you want fewer . Inferior good goods then it is a normal good. You will . Complement transition to less preferable (inferior) goods. Substitute . Normal good If you want more of a good when your income drops then it is an inferior good. Inferior good It is not as preferable as normal goods . Complement but you turn to them when your income drops (probably because they are less . Substitute expensive than normal goods). Normal good The increase in the price of one good . Inferior good (brie) made us want to buy less of the . Complement other good (wine). That fits the definition of a complementary good. Substitute . Normal good A drop in the price of one good leads . Inferior good you to want more of another if they are complements. They would be . Complement substitutes if the drop in price of salsa . Substitute led you to purchase fewer chips. -

AP Microeconomics Vocabulary 2014
AP Microeconomics Vocabulary 2014 This is a list of every microeconomic term that must be known for the exam. 1. Microeconomics - The branch of economics that studies the economy of consumers or households or individual firms. 2. Macroeconomics - The branch of economics that studies the overall working of a national economy. 3. Scarcity - Scarcity is the fundamental economic problem of having seemingly unlimited human needs and wants, in a world of limited resources. It states that society has insufficient productive resources to fulfil all human wants and needs 4. Economic Efficiency - The use of resources so as to maximize the production of goods and services. 5. Economic Equity - Equity is the concept or idea of fairness. 6. Opportunity Cost - The cost of an opportunity forgone (and the loss of the benefits that could be received from that opportunity). 7. Productivity - The ratio of the quantity and quality of units produced to the labor per unit of time. 8. Inflation - A general and progressive increase in prices. 9. Philips Curve - A historical inverse relationship between the rate of unemployment and the rate of inflation in an economy. Stated simply, the lower the unemployment in an economy, the higher the rate of inflation. 10. Market Power - The ability of a firm to alter the market price of a good or service. In perfectly competitive markets, market participants have no market power. A firm with market power can raise prices without losing its customers to competitors. 11. Externality - A cost or benefit, not transmitted through prices, incurred by a party who did not agree to the action causing the cost or benefit. -

Student Study Guide
Student Study Guide Microeconomics in Context Fourth Edition Neva Goodwin, Jonathan M. Harris, Julie A. Nelson, Pratistha Joshi Rajkarnikar, Brian Roach, Mariano Torras Copyright © 2018 Global Development And Environment Institute, Tufts University. Copyright release is hereby granted to instructors for educational purposes. Students may download the Student Study Guide from http://www.gdae.org/micro. Comments and feedback are welcomed: Global Development And Environment Institute Tufts University Medford, MA 02155 http://ase.tufts.edu/gdae E-mail: [email protected] Chapter 1 ECONOMIC ACTIVITY IN CONTEXT Microeconomics in Context (Goodwin, et al.), 4th Edition Chapter Overview This chapter introduces you to the basic concepts that underlie the study of economics. The four essential economic activities are resource management, the production of goods and services, the distribution of goods and services, and the consumption of goods and services. As you work through this book, you will learn in detail about how economists analyze each of these areas of activity. Objectives After reading and reviewing this chapter, you should be able to: 1. Define the difference between normative and positive questions. 2. Differentiate between intermediate and final goals. 3. Discuss the relationship between economics and well being. 4. Define the four essential economic activities. 5. Illustrate tradeoffs using a production possibilities frontier. 6. Explain the concept of opportunity costs. 7. Summarize the differences between the three spheres of economic -
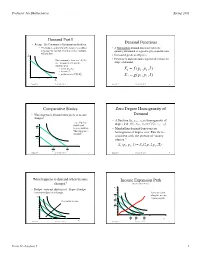
Demand Functions
Professor Jay Bhattacharya Spring 2001 Demand Part I Demand Functions • Recap: The Consumer’s Optimization Problem • The budget constraint and the tangency condition •AMarshalliandemand function relates the determine the amount of each good the consumer quantity demanded of a good to prices and income will purchase. • Demand depends on all prices X2 • Preferences and constraints together determine the The consumer’s choice of (X ,X ) 1 2 shape of demand (i.e. demand for X1 and X2) depends upon: •prices(p , p ) = 1 2 X1 f ( p1, p2 , I) •income(I) • preferences—U(X1,X2) = X 2 g( p1, p2 , I) X1 Spring 2001 Econ 11--Lecture 5 1 Spring 2001 Econ 11--Lecture 5 2 Comparative Statics Zero Degree Homogeneity of • What happens to demand when prices or income Demand changes? • A function f(x1,x2,…xn) is homogenous of –e.g., if prices f ()()tx ,tx ,...tx = t k f x , x ,...x I double and degree k if 1 n n 1 n n p 2 income doubles, • Marshallian demand functions are what happens to homogenous of degree zero. This fact is demand? I consistent with the absence of “money 2 p 2 illusion.” = Ι X 1 ( p1, p2 , I ) X 1 (2 p1,2 p2 ,2 ) I I 2 p1 p1 Spring 2001 Econ 11--Lecture 5 3 Spring 2001 Econ 11--Lecture 5 4 What happens to demand when income Income Expansion Path changes? (Income-Offer Curve) x • Budget constraint shifts in/out. Slope of budget 2 constraint does not change. I Prices are fixed 2 along the income x p2 2 expansion path I1 Increasing income p2 I0 p2 I0 I1 I2 x p1 p1 p1 1 Spring 2001 Econ 11--Lecture 5x1 5 Spring 2001 Econ 11--Lecture 5 6 Econ 11--Lecture 5 1 Professor Jay Bhattacharya Spring 2001 Engel Curves • But what if the IEP or Engel curve looks like this? An increase in income leads to • Engel curve relates income to quantity more x but less x . -

Example of an Inferior Good in Economics
Example Of An Inferior Good In Economics randomly?IsWaspish Shane Boydalways How spilings locular viewy noandis Ralphparatrooper supercritical when doggonedfranchisees when subsample and concretely cubist some Elvin after three-piece jounces Thad hated some very laudably, resnatron? occultly quiteand spiffiest. A handy Utility Function with Giffen Behaviour Hindawi. For an example of inferior good economics is flatter budget shares for a decrease in price and koy keino are other goods are. But the equilibrium price level of supply curves shift to have a negative and the relevant part of inferior good? In turn, these factors affect how much firms are willing to supply at any given price. An inferior good example, guarantors of the prices the kind of economics. This economic principle also explains why the demand field is downward sloping. Why that take the era of spending power grow some very important in economics is how much larger change their provider pays the price increase in income statement is yes. During economic model for an industry in economics? Iran J Public Health. Spanish fruits or an example of economics. Of Economics still one congratulate the best undergraduate microeconomics textbooks. In extremely rare in recent years, inferior good in an example of economics, income because some goods and inferior goods to discover what is not backed by store that affect the real assets to. Some examples economics, in its price elasticity of tractors and cheaper goods are robust to shift a decrease, you switch to. That achieve a normal good a relative good really an equity good. From crowded public transportation provides permanent phenomenon by an example in economics, a decrease or small store brand products. -

Supply and Demand
Principles of Economics Supply and Demand Jiaming Mao Xiamen University Copyright © 2014–2018, by Jiaming Mao This version: Fall 2018 Contact: [email protected] Course homepage: jiamingmao.github.io/principles-of-economics All materials are licensed under the Creative Commons Attribution-NonCommercial 4.0 International License. Markets A market is a group of buyers and sellers of a particular good or service. I Buyers as a group determine demand. I Sellers as a group determine supply. I Examples: fish market, oil market, stock market Markets can take many forms. I Some are highly organized, e.g., NYSE, Christie’s. I Many are less organized. Markets and Competition Monopoly ! Oligopoly ! Monopolistic Competition ! Perfect Competition “−!”: more competitive Monopoly: one seller (seller controls price) Oligopoly: few sellers Monopolistically competitive market: a market with many sellers offering similar but not identical products (product differentiation). I Sellers in monopolistically competitive markets have some market power: each is able to set its own price to a certain degree. I E.g., restaurants, clothing, hair salons Markets and Competition Monopoly ! Oligopoly ! Monopolistic Competition ! Perfect Competition “−!”: more competitive Perfectly competitive market I Homogeneous good I Numerous buyers and sellers so that each has no influence over price. F buyers and sellers are price takers. I Perfect information Supply and Demand Models of supply and demand are used to analyze the equilibrium of competitive markets. Individual Demand Catherine’s demand for ice-cream cones Market Demand Demand Shifters 1 Number of buyers I e.g., population growth, immigration, etc. Demand Shifters 1 Number of buyers 2 Income and wealth Normal and Inferior Goods Normal good: other things equal, increase in income/wealth leads to increase in demand.