Sine and Cosine Radians for the first Eight Lectures of This Class, We Restricted Our Attention to Polynomial Functions of One Form Or Another
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
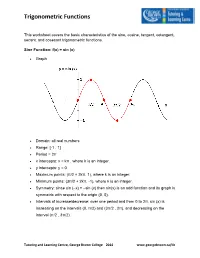
Trigonometric Functions
Trigonometric Functions This worksheet covers the basic characteristics of the sine, cosine, tangent, cotangent, secant, and cosecant trigonometric functions. Sine Function: f(x) = sin (x) • Graph • Domain: all real numbers • Range: [-1 , 1] • Period = 2π • x intercepts: x = kπ , where k is an integer. • y intercepts: y = 0 • Maximum points: (π/2 + 2kπ, 1), where k is an integer. • Minimum points: (3π/2 + 2kπ, -1), where k is an integer. • Symmetry: since sin (–x) = –sin (x) then sin(x) is an odd function and its graph is symmetric with respect to the origin (0, 0). • Intervals of increase/decrease: over one period and from 0 to 2π, sin (x) is increasing on the intervals (0, π/2) and (3π/2 , 2π), and decreasing on the interval (π/2 , 3π/2). Tutoring and Learning Centre, George Brown College 2014 www.georgebrown.ca/tlc Trigonometric Functions Cosine Function: f(x) = cos (x) • Graph • Domain: all real numbers • Range: [–1 , 1] • Period = 2π • x intercepts: x = π/2 + k π , where k is an integer. • y intercepts: y = 1 • Maximum points: (2 k π , 1) , where k is an integer. • Minimum points: (π + 2 k π , –1) , where k is an integer. • Symmetry: since cos(–x) = cos(x) then cos (x) is an even function and its graph is symmetric with respect to the y axis. • Intervals of increase/decrease: over one period and from 0 to 2π, cos (x) is decreasing on (0 , π) increasing on (π , 2π). Tutoring and Learning Centre, George Brown College 2014 www.georgebrown.ca/tlc Trigonometric Functions Tangent Function : f(x) = tan (x) • Graph • Domain: all real numbers except π/2 + k π, k is an integer. -

Lesson 6: Trigonometric Identities
1. Introduction An identity is an equality relationship between two mathematical expressions. For example, in basic algebra students are expected to master various algbriac factoring identities such as a2 − b2 =(a − b)(a + b)or a3 + b3 =(a + b)(a2 − ab + b2): Identities such as these are used to simplifly algebriac expressions and to solve alge- a3 + b3 briac equations. For example, using the third identity above, the expression a + b simpliflies to a2 − ab + b2: The first identiy verifies that the equation (a2 − b2)=0is true precisely when a = b: The formulas or trigonometric identities introduced in this lesson constitute an integral part of the study and applications of trigonometry. Such identities can be used to simplifly complicated trigonometric expressions. This lesson contains several examples and exercises to demonstrate this type of procedure. Trigonometric identities can also used solve trigonometric equations. Equations of this type are introduced in this lesson and examined in more detail in Lesson 7. For student’s convenience, the identities presented in this lesson are sumarized in Appendix A 2. The Elementary Identities Let (x; y) be the point on the unit circle centered at (0; 0) that determines the angle t rad : Recall that the definitions of the trigonometric functions for this angle are sin t = y tan t = y sec t = 1 x y : cos t = x cot t = x csc t = 1 y x These definitions readily establish the first of the elementary or fundamental identities given in the table below. For obvious reasons these are often referred to as the reciprocal and quotient identities. -

Calculus Terminology
AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential -

Derivation of Sum and Difference Identities for Sine and Cosine
Derivation of sum and difference identities for sine and cosine John Kerl January 2, 2012 The authors of your trigonometry textbook give a geometric derivation of the sum and difference identities for sine and cosine. I find this argument unwieldy | I don't expect you to remember it; in fact, I don't remember it. There's a standard algebraic derivation which is far simpler. The only catch is that you need to use complex arithmetic, which we don't cover in Math 111. Nonetheless, I will present the derivation so that you will have seen how simple the truth can be, and so that you may come to understand it after you've had a few more math courses. And in fact, all you need are the following facts: • Complex numbers are of the form a+bi, where a and b are real numbers and i is defined to be a square root of −1. That is, i2 = −1. (Of course, (−i)2 = −1 as well, so −i is the other square root of −1.) • The number a is called the real part of a + bi; the number b is called the imaginary part of a + bi. All the real numbers you're used to working with are already complex numbers | they simply have zero imaginary part. • To add or subtract complex numbers, add the corresponding real and imaginary parts. For example, 2 + 3i plus 4 + 5i is 6 + 8i. • To multiply two complex numbers a + bi and c + di, just FOIL out the product (a + bi)(c + di) and use the fact that i2 = −1. -

Complex Numbers and Functions
Complex Numbers and Functions Richard Crew January 20, 2018 This is a brief review of the basic facts of complex numbers, intended for students in my section of MAP 4305/5304. I will discuss basic facts of com- plex arithmetic, limits and derivatives of complex functions, power series and functions like the complex exponential, sine and cosine which can be defined by convergent power series. This is a preliminary version and will be added to later. 1 Complex Numbers 1.1 Arithmetic. A complex number is an expression a + bi where i2 = −1. Here the real number a is the real part of the complex number and bi is the imaginary part. If z is a complex number we write <(z) and =(z) for the real and imaginary parts respectively. Two complex numbers are equal if and only if their real and imaginary parts are equal. In particular a + bi = 0 only when a = b = 0. The set of complex numbers is denoted by C. Complex numbers are added, subtracted and multiplied according to the usual rules of algebra: (a + bi) + (c + di) = (a + c) + (b + di) (1.1) (a + bi) − (c + di) = (a − c) + (b − di) (1.2) (a + bi)(c + di) = (ac − bd) + (ad + bc)i (1.3) (note how i2 = −1 has been used in the last equation). Division performed by rationalizing the denominator: a + bi (a + bi)(c − di) (ac − bd) + (bc − ad)i = = (1.4) c + di (c + di)(c − di) c2 + d2 Note that denominator only vanishes if c + di = 0, so that a complex number can be divided by any nonzero complex number. -

Inverse Trig Functions Summary
Inverse trigonometric functions 1 1 z = sec ϑ The inverse sine function. The sine function restricted to [ π, π ] is one-to-one, and its inverse on this 3 − 2 2 ϑ = π ϑ = arcsec z interval is called the arcsine (arcsin) function. The domain of arcsin is [ 1, 1] and the range of arcsin is 2 1 1 1 −1 [ π, π ]. Below is a graph of y = sin ϑ, with the the part over [ π, π ] emphasized, and the graph − 2 2 − 2 2 of ϑ y. π 1 = arcsin ϑ = 2 π y = sin ϑ ϑ = arcsin y 1 π π 2 π − 1 ϑ 1 1 z − 1 π 1 π ϑ 1 1 y − 2 2 − 1 − 1 1 3 π ϑ = 2 π ϑ = 2 π − 2 By definition, By definition, 1 1 1 3 ϑ = arcsin y means that sin ϑ = y and π 6 ϑ 6 π. ϑ = arcsec z means that sec ϑ = t and 0 6 ϑ< 2 π or π 6 ϑ< 2 π. − 2 2 Differentiating the equation on the right implicitly with respect to y, gives Again, differentiating the equation on the right implicitly with respect to z, and using the restriction in ϑ, dϑ dϑ 1 1 1 one computes the derivative cos ϑ = 1, or = , provided π<ϑ< π. dy dy cos ϑ − 2 2 d 1 (arcsec z)= 2 , for z > 1. 1 1 2 2 dz z√z 1 | | Since cos ϑ> 0 on ( 2 π, 2 π ), it follows that cos ϑ = p1 sin ϑ = p1 y . -

American Protestantism and the Kyrias School for Girls, Albania By
Of Women, Faith, and Nation: American Protestantism and the Kyrias School For Girls, Albania by Nevila Pahumi A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy (History) in the University of Michigan 2016 Doctoral Committee: Professor Pamela Ballinger, Co-Chair Professor John V.A. Fine, Co-Chair Professor Fatma Müge Göçek Professor Mary Kelley Professor Rudi Lindner Barbara Reeves-Ellington, University of Oxford © Nevila Pahumi 2016 For my family ii Acknowledgements This project has come to life thanks to the support of people on both sides of the Atlantic. It is now the time and my great pleasure to acknowledge each of them and their efforts here. My long-time advisor John Fine set me on this path. John’s recovery, ten years ago, was instrumental in directing my plans for doctoral study. My parents, like many well-intended first generation immigrants before and after them, wanted me to become a different kind of doctor. Indeed, I made a now-broken promise to my father that I would follow in my mother’s footsteps, and study medicine. But then, I was his daughter, and like him, I followed my own dream. When made, the choice was not easy. But I will always be grateful to John for the years of unmatched guidance and support. In graduate school, I had the great fortune to study with outstanding teacher-scholars. It is my committee members whom I thank first and foremost: Pamela Ballinger, John Fine, Rudi Lindner, Müge Göcek, Mary Kelley, and Barbara Reeves-Ellington. -

A Note on the History of Trigonometric Functions and Substitutions
A NOTE ON THE HISTORY OF TRIGONOMETRIC FUNCTIONS AND SUBSTITUTIONS Jean-Pierre Merlet INRIA, BP 93, 06902 Sophia-Antipolis Cedex France Abstract: Trigonometric functions appear very frequently in mechanism kinematic equations (for example as soon a revolute joint is involved in the mechanism). Dealing with these functions is difficult and trigonometric substi- tutions are used to transform them into algebraic terms that can be handled more easily. We present briefly the origin of the trigonometric functions and of these substitutions. Keywords: trigonometric substitutions, robotics 1 INTRODUCTION When dealing with the kinematic equations of a mechanism involving revolute joints appears frequently terms involving the sine and cosine of the revolute joint angles. Hence when solving either the direct or inverse kinematic equa- tions one has to deal with such terms. But the problem is that the geometric structure of the manifold build on such terms is not known and that only nu- merical method can be used to solve such equations. A classical approach to deal with this problem is to transform these terms into algebraic terms using the following substitution: θ 2t 1 − t2 t = tan( ) ⇒ sin(θ)= cos(θ)= 2 1+ t2 1+ t2 This substitution allows one to transform an equation involving the sine and cosine of an angle into an algebraic equation. Such type of equation has a structure that has been well studied in the past and for which a large number properties has been established, such as the topology of the resulting man- ifold and its geometrical properties. Furthermore efficient formal/numerical methods are available for solving systems of algebraic equations. -

Dept. of Urban Planning Dept
Document of The World Bank FOR OFFICIAL USE ONLY Public Disclosure Authorized Report No: 38354 - AL PROJECT APPRAISAL DOCUMENT ON A PROPOSED LOAN IN THE AMOUNT OF EUR 15.2 MILLION Public Disclosure Authorized (US$19.96 MILLION EQUIVALENT) AND A PROPOSED CREDIT IN THE AMOUNT OF SDR 10 MILLION (US$15 MILLION EQUIVALENT) TO ALBANIA Public Disclosure Authorized FOR A LAND ADMINISTRATION AND MANAGEMENT PROJECT January 3,2007 Environmentally & Socially Sustainable Development Sector Unit Europe and Central Asia Public Disclosure Authorized This document has a restricted distribution and may be used by recipients only in the performance of their official duties. Its contents may not otherwise be disclosed without World Bank authorization. CURRENCY EQUIVALENTS (Exchange Rate Effective December 5,2006) Currency Unit = Albanian Lek (ALL) ALL93.48 = US$1 US$O.Ol = ALL 1 1 Euro = 1.3137 US$ 1 SDR = 1.50435 US$ FISCAL YEAR January 1 - December 31 ABBREVIATIONS AND ACRONYMS CAS Country Assistance Strategy CDS City Development Strategy EMP Environmental Management Plan EPF Environmental Policy Framework ERR Economic Rate ofReturn EU European Union FY Fiscal Year IBRD International Bank for Reconstruction and Development IDA International Development Agency ILO International Labor Organization IPRO Immovable Property Registration Office LAMP Land Administration and Management Project MoI Ministry of Interior MPWTT Ministry ofPublic Works, Transport and Telecommunication M&E Monitoring and Evaluation NGO Non-governmental Organization OSCE Organization -

Sine and Cosine Functions and Their Derivatives
ERTH 430: The Sine and Cosine Functions Dr. Dave Dempsey Fluid Dynamics and their Derivatives Dept. of Earth in Earth Systems & Climate Sciences, SFSU I. Functions A function is a rule that associates each member of one set of values (the independent variable) to a value in another set of values (the dependent variable). II. Sine and Cosine Functions For these two trigonometric functions, we can ask, what is the independent variable, and what is the rule that associates values of the independent variable to values of the dependent variable? First, some context. Set up a two-dimensional rectangular coordinate system. Pick a point anywhere, and draw a line from the origin of the coordinate system to your point. Call the coordinates of this point x and y. Call the distance from the origin to this point d. (See the diagram below.) The x-axis and the line from the origin to the point intersect and form an angle. Call this angle, measured counterclockwise from the x- axis, θ. [Note: Although we define units for measuring angles (namely, degrees or radians), angles are dimensionless quantities. Who would have thought it: a dimensionless quantity that has units!] So, for the sine and cosine functions, what is the independent variable? Answer: the angle, θ. For the sine function, what is the rule d that associates θ with the value of the y dependent variable (that is, the sine of θ, or θ sin(θ))? It is as follows: Given a value of θ as x defined above, divide the y-coordinate of the point by the distance of the point from the origin, d. -

High School Mathematics Glossary Pre-Calculus
High School Mathematics Glossary Pre-calculus English-Chinese BOARD OF EDUCATION OF THE CITY OF NEW YORK Board of Education of the City of New York Carol A. Gresser President Irene H. ImpeUizzeri Vice President Louis DeSario Sandra E. Lerner Luis O. Reyes Ninfa Segarra-Velez William C. Thompson, ]r. Members Tiffany Raspberry Student Advisory Member Ramon C. Cortines Chancellor Beverly 1. Hall Deputy Chancellor for Instruction 3195 Ie is the: policy of the New York City Board of Education not to discriminate on (he basis of race. color, creed. religion. national origin. age. handicapping condition. marital StatuS • .saual orientation. or sex in itS eduacional programs. activities. and employment policies. AS required by law. Inquiries regarding compiiulce with appropriate laws may be directed to Dr. Frederick..6,.. Hill. Director (Acting), Dircoetcr, Office of Equal Opporrurury. 110 Livingston Screet. Brooklyn. New York 11201: or Director. Office for o ..·ij Rights. Depa.rtmenc of Education. 26 Federal PJaz:t. Room 33- to. New York. 'Ne:w York 10278. HIGH SCHOOL MATHEMATICS GLOSSARY PRE-CALCULUS ENGLISH - ClllNESE ~ 0/ * ~l.tt Jf -taJ ~ 1- -jJ)f {it ~t ~ -ffi 'ff Chinese!Asian Bilingual Education Technical Assistance Center Division of Bilingual Education Board of Education of the City of New York 1995 INTRODUCTION The High School English-Chinese Mathematics Glossary: Pre calculus was developed to assist the limited English proficient Chinese high school students in understanding the vocabulary that is included in the New York City High School Pre-calculus curricu lum. To meet the needs of the Chinese students from different regions, both traditional and simplified character versions are included. -

The Sine and Cosine Functions the Graphs of Sine and Cosine in the Last Lecture, We Defined the Quantities Sin Θ and Cos Θ for All Angles Θ
The Sine and Cosine Functions The Graphs of Sine and Cosine In the last lecture, we defined the quantities sin θ and cos θ for all angles θ. Today we explore the sine and cosine functions, their properties, their derivatives, and variations on those two functions. By now, you should have memorized the values of sin θ and cos θ for all of the special angles. For the purposes of completeness, we recreate the tables of these values from the last lecture below: θ cos θ sin θ θ cos θ sin θ 0 1 0 p p 7¼ - 3 - 1 ¼ 3 1 6 p2 p2 6 p2 p2 5¼ ¡ 2 ¡ 2 ¼ 2 2 4 2 p2 4 2 p2 4¼ 1 3 ¼ 1 3 3 ¡ 2 ¡ 2 3 2 2 3¼ 0 -1 ¼ 0 1 2 p 2 p 5¼ 1 ¡ 3 2¼ ¡ 1 3 3 p2 p2 3 p2 p2 7¼ 2 ¡ 2 3¼ - 2 2 4 p2 2 4 p2 2 11¼ 3 ¡ 1 5¼ - 3 1 6 2 2 6 2 2 2¼ 1 0 ¼ -1 0 Clearly, we can plot the function f(x) = sin x and the function g(x) = cos x (replacing θ with x) using p p 2 3 ¼ ¼ ¼ the numerical tables above. We note that 2 ¼ 0:71, 2 ¼ 0:87, ¼ ¼ 3:14, 2 ¼ 1:57, 4 ¼ 0:79, 6 ¼ 0:52, ¼ and 3 ¼ 1:05. The resulting graph of f(x) = sin x looks like the following: we begin at the origin and with a positive slope of 1. As x increases, the slope of the sine function decreases, so that the derivative is 0 when we get ¼ to the point ( 2 ; 1), which is a local maximum for sin x.