Assessment of Delhi Ncr Traffic Using Queuing Model
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
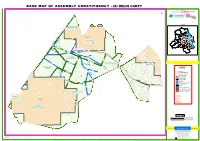
Base Map of Assembly Constituency
BASE MAP OF ASSEMBLY CONSTITUENCY - 38 / DELHI CANTT E E izfrcaf/kr dsoy foHkkxh; Á;®x gsrq RESTRICTED FOR DEPARTMENTAL USE ONLY fu;kZr ds fy, ugha NOT FOR EXPORT =(: µ M A H A T M (: A = G A N D H I M A K R G R I N G R O . A D K INDEX MAP MCD WARD NO- CANT_1, DELHI CANTT CHARGE 1 SH ANKA R LAL GALI DR-17 K TODAPUR 1 7 K 2 5 Kendriya 4 70 6 13 69 Vidyalaya 14 No.3 68 RESTRICTED 8 3 CA 9 18 66 MP 10 12 67 BE 17 63 LL AREA R 15 16 OA 65 64 D 11 62 19 20 61 26 25 24 23 22 60 27 59 31 29 21 MCD WARD NO- CANT_2, 39 KIRBY 28 58 PLACE 32 30 56 DELHI CANTONMENT DELHI CANTT 40 41 57 RAILWAY STATION 33 I2 37 55 CHARGE 2 35 38 38 0 BRAR 42 SQUARE 44 6 -1 34 51 R 43 D 4 50 - Cantonment 36 R 54 CA D Board Sr. RIA PP Sec. School K A M 45 52 AR 48 G S TA TI ON 53 RO 49 AD CHANDAN 47 HOS ROAD PITAL AL SINGH PARK RO SPIT AD HO HO SP ITA NANGAL L R OAD RING ROAD P S AD AN ER RO K -19 V COLONY 46 A HA DR IC KH R 20 E AN OA DR- LA P D NE DIPLOMATIC D P A Cantonment AN ENCLAVE K CHANDAN O G K P HA R Board Sec. -

1 DELHI TRAFFIC POLICE TRAFFIC ADVISORY Traffic Arrangements
DELHI TRAFFIC POLICE TRAFFIC ADVISORY Traffic Arrangements – Republic Day Celebrations on 26Th January, 2021 Republic Day will be held on 26th January, 2021. The Parade will start at 9.50 AM from Vijay Chowk and proceed to National Stadium, whereas Tableaux will start from Vijay Chowk and proceed to Red Fort Ground . There will be wreath laying function at National War Memorial at 09.00 AM. There would be elaborate traffic arrangements and restrictions in place for smooth conduct of the Parade and Tableaux along the respective routes. ROUTE OF THE PARADE/TABLEAUX :- (A) Parade Route:- Vijay Chowk- Rajpath- Amar Jawan Jyoti- India Gate- R/A Princess Palace-T/L Tilak Marg Radial Road- Turn right on “C” Hexagon- Turn left and enter National Stadium from Gate No. 1. (B) Tableaux Route :- Vijay Chowk- Rajpath- Amar Jawan Jyoti- India Gate- R/A Princess Palace-T/L Tilak Marg - Bahadur Shah Zafar Marg – Netaji Subhash Marg - Red Fort. TRAFFIC RESTRICTIONS In order to facilitate smooth passage of the Parade, movement of traffic on certain roads leading to the route of the Parade and Tableaux will be restricted as under:- (1). No traffic will be allowed on Vijay Chowk from 06.00 PM on 25.01.2021 till Parade is over. Rajpath is already out of bounds. (2). No cross traffic on Rajpath intersections from 11.00 PM on 25.01.2021 at Rafi Marg, Janpath, Man Singh Road till Parade is over. (3). ‘C’-Hexagon-India Gate will be closed for traffic from 05.00 AM on 26.01.2021 till Tableaux crosses Tilak Marg. -
Downlod Bus Routes
Number of Buses in S. No. Cluster No Route No. From To operation (varies Via Depot Buses Booking Status Availability Status from time to time) Azadpur,Wazir Pur Depot, Punjabi Bagh, Zakhira, Moti Nagar, Shadi 1 3 78 Azadpur Inderpuri (Krishi Kunj) 19 BBM Depot AL 1 18 Pur Depot, Lohi Mandi,Inderpuri (Krishi Kunj) Nehru Vihar,Balak Ram Hospital,Khalsa College,Shakti Nagar Nagia Park,Gulabi Bagh,Shastri Nagar E Block,Zakhira,Moti Nagar,P/S Kirti 2 4 108 Nehru Vihar Hari Nagar Clock Tower 17 BBM Depot AL 1 16 Nagar,Maya Puri Xing / Maya Puri Depot,Beri Wala Bagh,Hari Nagar Clock Tower Nathu Pura,Kaushik Enclave,Jharoda Xing Transport Authority (Burari),Nirankari Colony (Radio Colony),GTB Nagar,Old Sectt,ISBT 3 3 185 Nathupura Kendriya Terminal 7 (Kashmiri Gate),Red Fort,Delhi Gate,Vivekanand Marg,Palika BBM Depot AL 1 6 Kendra,Kendriya Terminal Church Road. Kalyan Vihar,Rana Pratap Bagh,P/S Roop Nagar/Roshnara Road,Delhi University,Balak Ram Hospital,Gur Nanak Sar,Bhajan Pura,C 4 4 3 262 Kalyan Vihar Harsh Vihar 4 Yamuna Vihar,Nand Nagari Depot,Harsh Vihar. BBM Depot AL 4 ISBT (Kashmere Gate),Old Sectt,Khalsa College,Shakti Nagar Nagia Park,Gulabi Bagh Xing,Shastri Nagar E Block,Zakhira,Moti Nagar,Raja Garden,Mukharji Park(Subhash Nagar Crossing),Tilak Nagar,Distret 5 3 813 ISBT Kashmere Gate Mangla Puri Terminal 11 Centre ,Uttam Nagar /A1 Janak Puri,C-1 Janakpuri, New Dabri BBM Depot AL 2 9 Road,Mangla Puri (T) Old Delhi Railway Station,Tis Hazari Animal Hospital/ Mori Gate,Ice Factory,Guru Govind Singh Marg,Sarai Rohila,Zakhira,Punjabi Bagh Old Delhi Railway 6 3 937A Sultanpuri Terminal 21 Terminal,Madipur JJ Colony,Peera Garhi Chowk,Mangolpuri B- BBM Depot AL 1 20 Station(Fatehpuri) Block,Mangolpuri S Block,Sultanpuri Terminal. -

Dhaula Kuan Bus Stop
DHAULA KUAN BUS STOP NOTE (TSR Only):- 1. Fare Rs.25/- for first fall of 2 km. (upon downing the meter) and thereafter Rs. 8.00 per kilometer for every additional kilometer. 2. Night charge 25% of the fare (11.00 PM to 5.00 AM) 3. Baggage Rs.7.50/- per piece (except shopping bag and small charge briefcase) 4. Waiting charge Rs.30/- for one hour (subject to minimum of 15 minutes stay) 5. Service The following is the tariff of Service Charges: - charges 1. Rs. 05/- Service Charge for Zones O TO B 2. Rs.10/- Service Charges for Zones (C TO M) KILOMETER WISE DESTINATION & FARE CHART FARE (including S. NO DESTINATION KILOMETER service charge) 1 A.P.BHAWAN 8-11 105 2 A.P.S.COLONY 5-8 80 3 ABUL FAZAL ENCLAVE 17-20 180 4 ADARSH NAGAR 20-23 205 5 ADHCHINI 8-11 105 6 AIIMS 5-8 80 7 AIR FORCE STATION PALAM 8-11 105 8 AJMERI GATE 8-11 105 9 AKBAR ROAD 8-11 105 10 ALAK NANDA 14-17 155 11 ALI PUR 29-32 275 12 ALI PUR ROAD 14-17 155 13 ALKA HOTEL 8-11 105 14 AMAR COLONY(LAJPAT NAGAR) 11-14 130 15 AMBASSADOR HOTEL 8-11 105 16 AMBEDKAR NAGAR 14-17 155 17 AMBIKA VIHAR 17-20 180 18 AMRITA SHER GILL MARG 8-11 105 19 ANAND LOK 8-11 105 20 ANAND NIKETAN 3-5 55 21 ANAND PARVAT 11-14 130 22 ANAND VIHAR 23-26 225 23 ANDHA MUGAL 14-17 155 24 ANDHERI MOUR 17-20 180 25 ANDREWJ GANJ 8-11 105 26 ANSARI NAGAR (A.I.I.M.S) 5-8 80 27 ANSARI ROAD (D. -

Delhi Police Colonies, Typewise As on 31.01.2020 Distt
DELHI POLICE COLONIES, TYPEWISE AS ON 08.09.2021 DISTT. Colony Name Qtr Type SOUTH DEFENCE COLONY A, B, C PC HAUZ KHAS A, B, C PS HAUZ KHAS A, B, C HAUZ KHAS COMPLEX D, E PS LODHI COLONY A, B, C MEHRAULI A, B, C FRRO LINES B, D MALVIYA NAGAR A, B, C PS AMBEDKAR NAGAR A, B, C CR PARK B, C, D GULMOHAR PARK E-1 GREATER KAILASH-1 (STAFF QTRS.) B, C, E GREATER KAILASH D (GNCT QTR) PC ANDREWS GANJ A, B, D (DANGEROUS DECLARED) SOUTH-WEST DHAULA KUAN A, B DELHI CANTT. (Staff qtrs.) B, C, D, E, E-1 SECTOR 12 R.K. PURAM A, B, C SECTOR 04 R.K. PURAM B SECTOR 08 R.K. PURAM A SAROJINI NAGAR A, B, C VASANT KUNJ B, C, D VASANT VIHAR A, B, C, D PC MEHRAM NAGAR (IGIA) A, B, C, D SOUTH -EAST AMAR COLONY C PS SARITA VIHAR B, C, D H.N.DIN A, C PS KALKAJI A, B, C, D PS GOVIND PURI A, B NEW FRIENDS COLONY A, B JANGPURA A, B SUNLIGHT COLONY A, B PS LAJPAT NAGAR A, B, C S.N. PURI B, C NEHRU PLACE A, B, C BADARPUR (PS & STAFF QTRS) B, C DWARKA JHARODA KALAN A, B, C, D PS UTTAM NAGAR A, B, C ZAFFAR PUR KALAN B, C, D DWARKA SECTOR -13 (PH-1 & 2) A, B DWARKA SECTOR -16-A B DWARKA SECTOR -16-B A DWARKA SECTOR -16-B (PHP) B, C, D, E DWARKA SECTOR -19 B, C DWARKA SECTOR -19 (SOUTH) B, C DWARKA SECTOR -23 B, C DWARKA SECTOR -09 B, C DWARKA SECTOR -17-C B, C, D DWARKA SECTOR -16-C B, C, D DWARKA SEC-09, PTS DWARKA (STAFF QTRS) B, D, E NAJAFGARH A, B (DANGEROUS) WEST HARI NAGAR B, C PS HARI NAGAR & STAFF QTRS. -

UNCLAIMED DEPOSIT LIST AS on 31/03/2020 S No. Customer Name Customer Address 1 KAMALA SETH SURESH SETH & NARE 4831/24, ANSAR
UNCLAIMED DEPOSIT LIST AS ON 31/03/2020 S No. Customer Name Customer Address 1 KAMALA SETH SURESH SETH & NARE 4831/24, ANSARI ROAD,,DARYA GANJ,,, 2 RAGHOO RAJ 26-F,KOHLAPUR ROAD,,KAMLA NAGAR,,, 3 CHOPRA SOUND 2432, TILAK STREET,,PAHAR GANJ,,PHONE OFF. 3528468,7520103, 4 R.K.TRADING CO. 11, RANI JHANSI ROAD,,,, 5 M.M. EXPORTS 512, CONNAUGHT PLACE,,,, 6 MAHUR ELECTRIC WORKS 74/76, JAGAN NATH TEMPLE,,OPP.NEW KOTWALI,DARYA GANJ, 7 BHARAT TENT HOUSE RAM NAGAR,,,, 8 DKG MANAGEMENT G-72 VIKAS MARG,,LAXMI NAGAR,,, 9 VIRENDER SHANKAR ARORA & NEHA 773/2, C.A. APPARTMENTS,,PASHIM VIHAR,,, 10 RAGHO RAJ 26-F,KHOLAPUR ROAD,,KAMLA NAGAR,,, 11 QUICK TEMPO SERVICE II/C-82, LAJPAT NAGAR,,, 12 SANKALP PRINTERS 4596/7, MAHABIR NIWAS,,11, DARYA GANJ,, 13 PRINT CRAFT 2003, GALI RAJA UGGER SAIN,,SITA RAM BAZAR,,, 14 RAJIV DHIR D-73, KALKAJI,,NEW DELHI. 110019,CARE; NO DEBIT ALLOWED, 15 HARISH KUMAR 130,INDIRA VIHAR,,OPP.B.B.M.DEPOT,,, 16 MICKY PROCESSING 1, ANSARI ROAD,,DARYA GANJ,,, 17 REEL EXPORTS 4226(A)/1,ANSARI ROAD,,DARYA GANJ,, 18 TEKNOCRATE SYSTEMS B-23/600 STREET NO.2,GANESH NAGAR II,, 19 PREM & CO. SD-184,PITAM PURA,,, 20 ARIHANT BOOK DISTRIBUTOR E-158/POCKET E,G.T.B. ENCLAVE,,, 21 THE HINDUSTAN TRUST (P) LTD. 11, DARYA GANJ,,,, 22 KARMOKAR & CO. 2240, GALI ANAR,KINARI BAZAR,, 23 SUDHAKAR ENTERPRISES SD-184, TOWER APARTMENTS,,PITAM PURA,,, 24 SARITA KHURANA D-429,DEFENCE COLONY,,, 25 S.D. & SONS 2188,KUCHA AQIL KHAN,BAZAR SITA RAM,, 26 SHILPA CO-OP GROUP HOUSING SOC 809, KATARA NEEL,,CHANDNI CHOWK,, 27 AISHA HANDICRAFTS C/O AZEEMUDDIN,GALI NO.10,,GHONDA NORTH,,, 28 ACTION COLOR LAB (P) LTD., 8-B, NETAJI SUBHASH MARG,,,, 29 MEDICARE ENGINEERS F-39/766, GANESH NAGAR II,,SHAKAR PUR,,, 30 MONICA OVERSEAS C/O. -

Delhi Metro Rail Corporation Ltd. ! "# $%& '()*+
DELHI METRO RAIL CORPORATION LTD. ! "# $%& '()*+, (A JOINT VENTURE OF GOVERNMENT OF INDIA AND GOVT. OF DELHI) (- . ! / 01 2) Metro Bhawan, 13,Fire Brigade Lane ,Barakhamba Road, New Delhi-110001 Ph. No.:23417910-12, Fax: 23418413 CIN: U74899DL1995GOI068150 PURCHASE ORDER/ 3 Purchase Order No./ 3 35003110 Date/ :04.07.2019 Tender No./ $% DMRCIT2856 Tender Opened on/ $% 40 : Vendor No./ 106965 GSTIN: 07AAACQ1105B1ZA To/ : Delivery Address/ : M/s Transtek Infoways Pvt. Ltd. DELHI METRO RAIL CORPORATION LTD. B-184 1st Floor, DDA Shed, Metro Bhawan , 13Fire Brigade Lane , Okhla Indl Area, PH-I, New Delhi- Barakhamba Road Ph.:01141088258. NEW DELHI-110001 GSTIN: Your Offer No./ E-TENDER Dated/ : 25.06.2019 Your offer cited above has been accepted for supply of the items mentioned below.Kindly arrange to deliver the material to the consignee with the terms and conditions as follows: ______________________________________________________________________ S.No. Description Plant Qty/Unit Rate(INR), GrossAmt (INR) / (INR) (INR) ______________________________________________________________________ 1 All-in-one Desktop PC with Intel core i7 COOF 1.000NO 68,850.00 68,850.00 , 8th gen, 8 GB RAM,1 TB hard drive, 23.8" display, DVD writer, Windows 10 Pro, Keyboard & Mouse with 3 years comprehensive onsite warranty. Vendor's offer-Dell 7460 Material no. : HSN/SAC : Delivery Date : 03.08.2019 2 Printer HP Color Laserjet Pro MFP M181fw COOF 2.000NO 41,030.00 82,060.00 or similar with 3 years comprehensive on-site warranty from OEM/Manufacturer. Vendor's offer-HP181 FW Material no. : HSN/SAC : Delivery Date : 03.08.2019 3 A3 color laserjet printer (Print/Scan/ COOF 1.000NO 289,100.00 289,100.00 Copy/Fax) (HP Color laserjet MFP M775F or similar) with 3 years comprehensive on-site warranty from OEM/Manufacturer. -

S.No. Station Name Station Landline No. Station Mobile No. Line 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 2
Updated List of Station Landline Telephone Numbers and Mobile Numbers S.No. Station Name Station Landline No. Station Mobile No. Line 1 New Bus Adda 7290018822 7303498348 2 Hindon River 07290018832 7303498347 3 Arthala 7290019646 7303498346 4 Mohan Nagar 7290018560 7303498345 5 Shyam Park 7290018557 7303498344 6 Rajender Nagar 7290018413 7303498343 7 Raj Bagh 7290018457 7303498342 8 Shahid Nagar 07290019023 7303498341 9 Dilshad Garden 7290049191 8800793100 10 Jhilmil 7290049044 8800793101 11 Mansarovar Park 7290048677 8800793102 12 Shahadra 7290048466 8800793103 13 Welcome 7290048366 8800793104 14 Seelampur 7290048299 8800793105 Line-1 15 Shastri Park 7290048282 8800793106 16 Kashmere Gate (Rail Corridor) 01123860837 8800793107 17 Tis Hazari 7290048155 8800793108 18 Pul Bangash 7290048122 8800793109 19 Pratap Nagar 7290048118 8800793110 20 Shastri Nagar 7290048055 8800793111 21 Inderlok 7290048022 8800793112 22 Kanahiya Nagar 7290048011 8800793113 23 Keshav Puram 7290047997 8800793114 24 Netaji Subhash Place 7290047966 8800793115 25 Kohat Enclave 7290047899 8800793116 26 Pitam Pura 7290047647 8800793117 27 Rohini East 7290047399 8800793118 28 Rohini West 7290047355 8800793119 29 Rithala 7290046922 8800793120 30 Samaypur Badli 7290020884 7042744337 31 Rohini Sector-18, 19 7290020885 7042744336 32 Haiderpur-Badli Mor 7290013837 7042744335 33 Jahangirpuri 7290052042 8800793121 34 Adarsh Nagar 7290052062 8800793122 35 Azadpur 7290052072 8800793123 36 Model Town 7290052082 8800793124 37 G.T.B Nagar 7290052092 8800793125 38 Vishwavidhyalaya -

Consultancy Proposal for Traffic Improvement Plan
PRESENTATION ON TRAFFIC IMPROVEMENT PLAN OF OUTER RING ROAD FROM IIT GATE TO NH-8 & ITS INFLUENCE AREA Public Works Department 5th April 2013 (Govt of NCT of Delhi) (A Government of India Enterprise) Traffic Scenes at RTR in Peak Hrs. from NH-8 to IIT 2 RITES LIMITED Vehicular & Pedestrian Movement Issues 4 ft. high footpath at Olof Little space for passenger Bottleneck on Poorvi Marg - Palme Marg boarding/alighting due to On ORR Jn. due to a narrow street parking near Munirka culvert Traffic Congestion under RTR Underutilized sub way at Bottleneck at the mouth of flyover from RTR junction to Munirka Junction RTR flyover towards Vasant Vihar RITES LIMITED NH8 3 Reasons for Overloading of RTR Access to Ring Road (RR) RTR Marg provides shortest link between RR and ORR and is only right turning facility between Dhaula Kuan and Africa Avenue towards RR Benito Juarez and Kama Kothi Marg do not have right turning facility to RR Thus, the traffic bound for RR from Southwest Delhi and Guraon loads RTR Jamming conditions at Dhaula Kuan (DK) Dhaula Kuan, a major link connecting West with Central & East of Delhi is loaded with traffic from Gurgaon; bound for Central , East Delhi Persistent traffic jams at Cariappa Marg Crossing and detour discourages this traffic to take DK to approach RR Absence of alternatives routes connecting Delhi & Gurgaon Underutilization of Roads B J Marg is highly underutilized due to non availability of right turn on RR and ORR Africa San Martin Marg is another highly under utilized Avenue Rd due to absence of network connectivity with BJM Nelson Mandela Road, the widest road of the Study Area highly underutilised Macro Level analysis of Traffic Problems Unprecedented growth Sonipat of Gurgaon, the IT hub, and high inter Rohtak dependence of Delhi Ghaziabad and Gurgaon Inadequate mass transport facility for Gurgaon, connecting Noida/ Delhi and its satellite G. -

611 Bus Time Schedule & Line Route
611 bus time schedule & line map 611 Arsd College (Dhaula Kuan) View In Website Mode The 611 bus line (Arsd College (Dhaula Kuan)) has 2 routes. For regular weekdays, their operation hours are: (1) Arsd College (Dhaula Kuan): 6:00 AM - 9:30 PM (2) Mayur Vihar Phase III Terminal / Paper Market: 7:10 AM - 9:40 PM Use the Moovit App to ƒnd the closest 611 bus station near you and ƒnd out when is the next 611 bus arriving. Direction: Arsd College (Dhaula Kuan) 611 bus Time Schedule 58 stops Arsd College (Dhaula Kuan) Route Timetable: VIEW LINE SCHEDULE Sunday 6:00 AM - 9:30 PM Monday 6:00 AM - 9:30 PM Mayur Vihar Phase III Terminal / Paper Market Tuesday 6:00 AM - 9:30 PM Sapera Basti Crossing Wednesday 6:00 AM - 9:30 PM Kerala School Thursday 6:00 AM - 9:30 PM Mayur Vihar Ph-Iii Friday 6:00 AM - 9:30 PM opp ryan international school Pankaj Mayur Plaza, Noida Saturday 6:00 AM - 9:30 PM CRPF Camp Mayur Vihar Phase III A1 Block Bharti Public School 611 bus Info Pragati Marg, Noida Direction: Arsd College (Dhaula Kuan) Stops: 58 New Kondali A1 Crossing Trip Duration: 70 min Line Summary: Mayur Vihar Phase III Terminal / Mayur Vihar Phase-Iii Crossing Paper Market, Sapera Basti Crossing, Kerala School, Mayur Vihar Ph-Iii, CRPF Camp, Mayur Vihar Phase III A1 Block, Bharti Public School, New Kondali A1 Ganpati Mandir Crossing, Mayur Vihar Phase-Iii Crossing, Ganpati Mandir, Fire Station, Dallu Pura, Kondali Old, Kalyan Fire Station Puri Terminal, Super Bazar, Chand Cinema, Trilokpuri 13-Block, Kotla Village, ITI Khichiripur, Pocket-5 Dallu Pura -

BY- ELECTION to DELHI MUNICIPAL CORPORATION -2016 Ward NO-168 Ward Name- NANAKPURA FINAL POLLING STATION LIST
BY- ELECTION TO DELHI MUNICIPAL CORPORATION -2016 Ward NO-168 Ward Name- NANAKPURA FINAL POLLING STATION LIST Serial_No_of_ Serial_No_of_ Ward _Polling Polling_Station_Loc Total_Elect AcNo PartNo Polling_Station_Building Area_Of_Polling_Station Electors_in_Ba Electors_in_Su Station_SNO ality ors sic Roll pp_Roll 1 - SATYA NIKETAN, MOTI BAGH 1 to 146; 2 - SHOP BLOCK, SATYA NIKETAN, MOTI BAGH, 1 to 18; 3 - SHIV MANDIR, SATYA NIKETAN, MOTI BAGH, MANDIR TO MANDIR; 4 - STAFF QUARTER SRI VENKATESHWARA SRI VENKATESHWAR COLLEGE DHAULA KUAN CANTEE, 1 TO 18; 5 - 1 44 1 SATYA NIKETAN 1145 COLLEGE, DHAULA KUAN SPRINGDALE SCHOOL, DHAULA KUAN, SCHOOL TO SCHOOL; 6 - INDIAN MOUNTAINEERING FOUNDATION, DHAULA KUAN, IMF TO IMF; 7 - SOUTH CAMPUS, DHAULA KUAN, 1 TO 5/8; 8 - S V COLLEGE HOSTEL, DHAULA KUAN, 1 TO 24 SRI VENKATESHWAR 1 - SATYA NIKETAN , MOTI BAGH, 147 TO 299; 2 - J J 2 44 2 SATYA NIKETAN 941 COLLEGE, DHAULA KUAN CAMP , SATYA NIKETAN 1 TO 500 SRI VENKATESHWAR 1 - MOTI BAGH VILLAGE, MOTI BAGH 1 TO 60; 2 - BARAT 3 44 3 SATYA NIKETAN GHAR, MOTI BAGH VILLAGE, BARAT GHAR TO BARAT 1038 COLLEGE, DHAULA KUAN GHAR SRI VENKATESHWAR 4 44 4 SATYA NIKETAN 1 - MOTI BAGH VILLAGE, NEW DELHI, 81 TO 165 749 COLLEGE, DHAULA KUAN 1 - MOTI BAGH VILLAGE, NEW DELHI, 166 TO 250; 2 - SRI VENKATESHWAR GURDWARA, MOTI BAGH, MOCHI BAGH VILLAGE, 1 TO 5 44 5 SATYA NIKETAN 8; 3 - SHRI RAM MANDIR, MOCHI BAGH VILLAGE, 755 COLLEGE, DHAULA KUAN MANDIR TO MANDIR; 4 - 25 YARDS PLOTS, MOCHI BAGH VILLAGE, 1 TO 40; GOVT CO-ED, SSS, 1 - S-283, SHASTRI MARKET JHUGGI, SOUTH MOTI 6 44 6 -

507CL Bus Time Schedule & Line Route
507CL bus time schedule & line map 507CL Arsd College / Dhaula Kuan View In Website Mode The 507CL bus line (Arsd College / Dhaula Kuan) has 2 routes. For regular weekdays, their operation hours are: (1) Arsd College / Dhaula Kuan: 6:00 AM - 9:20 PM (2) Okhla Extension (Abul Fazl Encalve): 6:50 AM - 9:50 PM Use the Moovit App to ƒnd the closest 507CL bus station near you and ƒnd out when is the next 507CL bus arriving. Direction: Arsd College / Dhaula Kuan 507CL bus Time Schedule 46 stops Arsd College / Dhaula Kuan Route Timetable: VIEW LINE SCHEDULE Sunday 6:00 AM - 9:20 PM Monday 6:00 AM - 9:20 PM Okhla Extension (Abul Fazl Encalve) Tuesday 6:00 AM - 9:20 PM Shaheen Bagh Thokar No. 8 (Af Enclave) Wednesday 6:00 AM - 9:20 PM Shaheen Bagh Thokar No. 7 Thursday 6:00 AM - 9:20 PM Shaheen Bagh Thokar No. 6 Friday 6:00 AM - 9:20 PM Aurangzeb Road, New Delhi Saturday 6:00 AM - 9:20 PM Shaheen Bagh Thokar No. 5 Unani Hospital / Okhla Ext Thokar 3 Nai Basti 507CL bus Info Direction: Arsd College / Dhaula Kuan Okhla Village Stops: 46 Trip Duration: 62 min Batla House Line Summary: Okhla Extension (Abul Fazl Encalve), Shaheen Bagh Thokar No. 8 (Af Enclave), Shaheen Maulana Mohamed Ali Jauhar Marg, New Delhi Bagh Thokar No. 7, Shaheen Bagh Thokar No. 6, Shaheen Bagh Thokar No. 5, Unani Hospital / Okhla Ansari Health Care Ext Thokar 3, Nai Basti, Okhla Village, Batla House, Ansari Health Care, Jamiya Millia College, Holy Jamiya Millia College Family Hospital, Bharat Nagar Crossing, Bharat Nagar, Taimur Nagar, Maharani Bagh (Ashram), Holy Family