A Note on Equilateral Polygons 23
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

1 Point for the Player Who Has the Shape with the Longest Side. Put
Put three pieces together to create a new 1 point for the player who has the shape. 1 point for the player who has shape with the longest side. the shape with the smallest number of sides. 1 point for the player who has the 1 point for the player with the shape that shape with the shortest side. has the longest perimeter. 1 point for the player with the shape that 1 point for each triangle. has the largest area. 1 point for each shape with 1 point for each quadrilateral. a perimeter of 24 cm. Put two pieces together to create a new shape. 1 point for the player with 1 point for each shape with the shape that has the longest a perimeter of 12 cm. perimeter. Put two pieces together to create a new shape. 1 point for the player with 1 point for each shape with the shape that has the shortest a perimeter of 20 cm. perimeter. 1 point for each 1 point for each shape with non-symmetrical shape. a perimeter of 19 cm. 1 point for the shape that has 1 point for each the largest number of sides. symmetrical shape. Count the sides on all 5 pieces. 1 point for each pair of shapes where the 1 point for the player who has the area of one is twice the area of the other. largest total number of sides. Put two pieces together to create a new shape. 1 point for the player who has 1 point for each shape with at least two the shape with the fewest number of opposite, parallel sides. -

Extremal Problems for Convex Polygons ∗
Extremal Problems for Convex Polygons ∗ Charles Audet Ecole´ Polytechnique de Montreal´ Pierre Hansen HEC Montreal´ Fred´ eric´ Messine ENSEEIHT-IRIT Abstract. Consider a convex polygon Vn with n sides, perimeter Pn, diameter Dn, area An, sum of distances between vertices Sn and width Wn. Minimizing or maximizing any of these quantities while fixing another defines ten pairs of extremal polygon problems (one of which usually has a trivial solution or no solution at all). We survey research on these problems, which uses geometrical reasoning increasingly complemented by global optimization meth- ods. Numerous open problems are mentioned, as well as series of test problems for global optimization and nonlinear programming codes. Keywords: polygon, perimeter, diameter, area, sum of distances, width, isoperimeter problem, isodiametric problem. 1. Introduction Plane geometry is replete with extremal problems, many of which are de- scribed in the book of Croft, Falconer and Guy [12] on Unsolved problems in geometry. Traditionally, such problems have been solved, some since the Greeks, by geometrical reasoning. In the last four decades, this approach has been increasingly complemented by global optimization methods. This allowed solution of larger instances than could be solved by any one of these two approaches alone. Probably the best known type of such problems are circle packing ones: given a geometrical form such as a unit square, a unit-side triangle or a unit- diameter circle, find the maximum radius and configuration of n circles which can be packed in its interior (see [46] for a recent survey and the site [44] for a census of exact and approximate results with up to 300 circles). -

Polygons and Convexity
Geometry Week 4 Sec 2.5 to ch. 2 test section 2.5 Polygons and Convexity Definitions: convex set – has the property that any two of its points determine a segment contained in the set concave set – a set that is not convex concave concave convex convex concave Definitions: polygon – a simple closed curve that consists only of segments side of a polygon – one of the segments that defines the polygon vertex – the endpoint of the side of a polygon 1 angle of a polygon – an angle with two properties: 1) its vertex is a vertex of the polygon 2) each side of the angle contains a side of the polygon polygon not a not a polygon (called a polygonal curve) polygon Definitions: polygonal region – a polygon together with its interior equilateral polygon – all sides have the same length equiangular polygon – all angels have the same measure regular polygon – both equilateral and equiangular Example: A square is equilateral, equiangular, and regular. 2 diagonal – a segment that connects 2 vertices but is not a side of the polygon C B C B D A D A E AC is a diagonal AC is a diagonal AB is not a diagonal AD is a diagonal AB is not a diagonal Notation: It does not matter which vertex you start with, but the vertices must be listed in order. Above, we have square ABCD and pentagon ABCDE. interior of a convex polygon – the intersection of the interiors of is angles exterior of a convex polygon – union of the exteriors of its angles 3 Polygon Classification Number of sides Name of polygon 3 triangle 4 quadrilateral 5 pentagon 6 hexagon 7 heptagon 8 octagon -

Englewood Public School District Geometry Second Marking Period
Englewood Public School District Geometry Second Marking Period Unit 2: Polygons, Triangles, and Quadrilaterals Overview: During this unit, students will learn how to prove two triangles are congruent, relationships between angle measures and side lengths within a triangle, and about different types of quadrilaterals. Time Frame: 35 to 45 days (One Marking Period) Enduring Understandings: • Congruent triangles can be visualized by placing one on top of the other. • Corresponding sides and angles can be marked using tic marks and angle marks. • Theorems can be used to prove triangles congruent. • The definitions of isosceles and equilateral triangles can be used to classify a triangle. • The Midpoint Formula can be used to find the midsegment of a triangle. • The Distance Formula can be used to examine relationships in triangles. • Side lengths of triangles have a relationship. • The negation statement can be proved and used to show a counterexample. • The diagonals of a polygon can be used to derive the formula for the angle measures of the polygon. • The properties of parallel and perpendicular lines can be used to classify quadrilaterals. • Coordinate geometry can be used to classify special parallelograms. • Slope and the distance formula can be used to prove relationships in the coordinate plane. Essential Questions: • How do you identify corresponding parts of congruent triangles? • How do you show that two triangles are congruent? • How can you tell if a triangle is isosceles or equilateral? • How do you use coordinate geometry -

Midsegment of a Trapezoid Parallelogram
Vocabulary Flash Cards base angles of a trapezoid bases of a trapezoid Chapter 7 (p. 402) Chapter 7 (p. 402) diagonal equiangular polygon Chapter 7 (p. 364) Chapter 7 (p. 365) equilateral polygon isosceles trapezoid Chapter 7 (p. 365) Chapter 7 (p. 402) kite legs of a trapezoid Chapter 7 (p. 405) Chapter 7 (p. 402) Copyright © Big Ideas Learning, LLC Big Ideas Math Geometry All rights reserved. Vocabulary Flash Cards The parallel sides of a trapezoid Either pair of consecutive angles whose common side is a base of a trapezoid A polygon in which all angles are congruent A segment that joins two nonconsecutive vertices of a polygon A trapezoid with congruent legs A polygon in which all sides are congruent The nonparallel sides of a trapezoid A quadrilateral that has two pairs of consecutive congruent sides, but opposite sides are not congruent Copyright © Big Ideas Learning, LLC Big Ideas Math Geometry All rights reserved. Vocabulary Flash Cards midsegment of a trapezoid parallelogram Chapter 7 (p. 404) Chapter 7 (p. 372) rectangle regular polygon Chapter 7 (p. 392) Chapter 7 (p. 365) rhombus square Chapter 7 (p. 392) Chapter 7 (p. 392) trapezoid Chapter 7 (p. 402) Copyright © Big Ideas Learning, LLC Big Ideas Math Geometry All rights reserved. Vocabulary Flash Cards A quadrilateral with both pairs of opposite sides The segment that connects the midpoints of the parallel legs of a trapezoid PQRS A convex polygon that is both equilateral and A parallelogram with four right angles equiangular A parallelogram with four congruent sides and four A parallelogram with four congruent sides right angles A quadrilateral with exactly one pair of parallel sides Copyright © Big Ideas Learning, LLC Big Ideas Math Geometry All rights reserved. -

Side of the Polygon Polygon Vertex of the Diagonal Sides Angles Regular
King Geometry – Chapter 6 – Notes and Examples Section 1 – Properties and Attributes of Polygons Each segment that forms a polygon is a _______side__ _ of ____ _the____ ______________. polygon The common endpoint of two sides is a ____________vertex _____of _______ the ________________polygon . A segment that connects any two nonconsecutive vertices is a _________________.diagonal Number of Sides Name of Polygon You can name a polygon by the number of its 3 Triangle sides. The table shows the names of some common polygons. 4 Quadrilateral 5 Pentagon If the number of sides is not listed in the table, then the polygon is called a n-gon where n 6 Hexagon represents the number of sides. Example: 16 sided figure is called a 16-gon 7 Heptagon 8 Octagon Remember! A polygon is a closed plane figure formed by 9 Nonagon three or more segments that intersect only at their endpoints. 10 Decagon 12 Dodecagon n n-gon All of the __________sides are congruent in an equilateral polygon. All of the ____________angles are congruent in an equiangular polygon. A __________________________regular polygon is one that is both equilateral and equiangular. If a polygon is ______not regular, it is called _________________irregular . A polygon is ______________concave if any part of a diagonal contains points in the exterior of the polygon. If no diagonal contains points in the exterior, then the polygon is ____________convex . A regular polygon is always _____________convex . Examples: Tell whether the figure is a polygon. If it is a polygon, name it by the number of sides. not a not a polygon, not a polygon, heptagon polygon hexagon polygon polygon Tell whether the polygon is regular or irregular. -
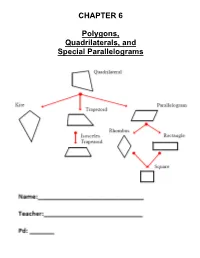
CHAPTER 6 Polygons, Quadrilaterals, and Special Parallelograms
CHAPTER 6 Polygons, Quadrilaterals, and Special Parallelograms Table of Contents DAY 1: (Ch. 6-1) SWBAT: Find measures of interior and exterior angles of polygons Pgs: 1-7 HW: Pgs: 8-10 DAY 2: (6-2) SWBAT: Solve Problems involving Parallelograms Pgs: 11-16 HW: Pgs: 17-18 DAY 3: (6-4) SWBAT: Solve Problems involving Rectangles Pgs: 19-22 HW: Pg: 23 DAY 4: (6-4) SWBAT: Solve Problems involving Rhombi and Squares Pgs: 24-28 HW: Pgs: 29-30 DAY 5: (6-6) SWBAT: Solve Problems involving Trapezoids Pgs: 31-36 HW: Pgs: 37-39 DAY 6-7: (Review) SWBAT: Review of Quadrilaterals Pgs: 40-52 HW: Finish this section for homework Chapter 6 (Section 1) – Day 1 Angles in polygons A polygon is a closed plane figure formed by three or more segments that intersect only at their endpoints. Each segment that forms a polygon is a side of the polygon. The common endpoint of two sides is a vertex of the polygon. A segment that connects any two nonconsecutive vertices is a diagonal. You can name a polygon by the number of its sides. The table shows the names of some common polygons. All the sides are congruent in an equilateral polygon. All the angles are congruent in an equiangular polygon. A regular polygon is one that is both equilateral and equiangular. If a polygon is not regular, it is called irregular. A polygon is concave if any part of a diagonal contains points in the exterior of the polygon. If no diagonal contains points in the exterior, then the polygon is convex. -

Sensitivity Studies for the Exercise I-1 of the OECD/UAM Benchmark
Hindawi Publishing Corporation Science and Technology of Nuclear Installations Volume 2012, Article ID 817185, 10 pages doi:10.1155/2012/817185 Research Article Sensitivity Studies for the Exercise I-1 of the OECD/UAM Benchmark E. Canuti,1 A. Petruzzi,1 F. D’Auria, 1 and T. Kozlowski2 1 San Piero a Grado Nuclear Research Group (GRNSPG), University of Pisa, Via Diotisalvi 2, 56122 Pisa, Italy 2 Department of Nuclear, Plasma, and Radiological Engineering, University of Illinois, 216 Talbot Laboratory, MC-234, 104 South Wright Street, Urbana, IL 61801, USA Correspondence should be addressed to E. Canuti, [email protected] Received 24 August 2012; Revised 30 October 2012; Accepted 31 October 2012 Academic Editor: Oscar Cabellos Copyright © 2012 E. Canuti et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. OECD/NEA has initiated an international Uncertainty Analysis in Modeling (UAM) benchmark focused on uncertainties in modeling of Light Water Reactor (LWR). The first step of uncertainty propagation is to perform sensitivity to the input data affected by the numerical errors and physical models. The objective of the present paper is to study the effect of the numerical discretization error and the manufacturing tolerances on fuel pin lattice integral parameters (multiplication factor and macroscopic cross- sections) through sensitivity calculations. The two-dimensional deterministic codes NEWT and HELIOS were selected for this work. The NEWT code was used for analysis of the TMI-1, PB-2, and Kozloduy-6 test cases; the TMI-1 test case was investigated using the HELIOS code. -
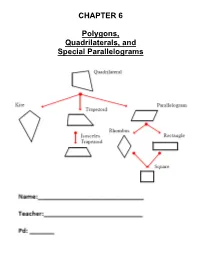
CHAPTER 6 Polygons, Quadrilaterals, and Special Parallelograms
CHAPTER 6 Polygons, Quadrilaterals, and Special Parallelograms Table of Contents DAY 1: (Ch. 6-1) SWBAT: Find measures of interior and exterior angles of polygons Pgs: 1-6 HW: Pgs: 7-8 #2 - 26, 29-41 (odd) DAY 2: (Ch. 6-1) SWBAT: Find measures of interior and exterior angles of polygons Pgs: 9-12 HW: Finish this section for homework DAY 3: (6-2) SWBAT: Solve Problems involving Parallelograms Pgs: 13-16 HW: Pgs: 17-18 DAY 4: (6-4) SWBAT: Solve Problems involving Rectangles Pgs: 19-22 HW: Pg: 23 DAY 5: (6-4) SWBAT: Solve Problems involving Rhombi and Squares Pgs: 24-28 HW: Pgs: 29-30 DAY 6: (6-6) SWBAT: Solve Problems involving Trapezoids Pgs: 31-36 HW: Pgs: 37-39 DAY 7: (Review) SWBAT: Review of Quadrilaterals Pgs: 40-47 HW: Finish this section for homework Chapter 6 (Section 1) – Day 1 Angles in polygons A polygon is a closed plane figure formed by three or more segments that intersect only at their endpoints. Each segment that forms a polygon is a side of the polygon. The common endpoint of two sides is a vertex of the polygon. A segment that connects any two nonconsecutive vertices is a diagonal. You can name a polygon by the number of its sides. The table shows the names of some common polygons. All the sides are congruent in an equilateral polygon. All the angles are congruent in an equiangular polygon. A regular polygon is one that is both equilateral and equiangular. If a polygon is not regular, it is called irregular. -

Refort Resumes
REFORT RESUMES ED 013 517 EC 000 574 NINTH GRADE PLANE AND SOLID GEOMETRY FOR THEACADEMICALLY TALENTED, TEACHERS GUIDE. OHIO STATE DEFT. Cf EDUCATION, COLUMBUS CLEVELAND FUBLIC SCHOOLS, OHIO FUD DATE 63 EDRS PRICE MF--$1.00 HC-$10.46 262F. DESCRIPTORS- *GIFTED, =PLANE GEOMETRY, *SOLID GEOMETRY, *CURRICULUM GUIDES, UNITS Cf STUDY (SUBJECTFIELDS), SPECIAL EDUCATION, GRADE 9, COLUMBUS A UNIFIED TWO--SEMESTER COURSE INPLANE AND SOLID GEOMETRY FOR THE GIFTED IS PRESENTED IN 15 UNITS,EACH SPECIFYING THE NUMBER OF INSTRUCTIONALSESSIONS REQUIRED. UNITS' APE SUBDIVIDED BY THE TOPIC ANDITS CONCEPTS, VOCABULARY, SYMBOLISM, REFERENCES (TO SEVENTEXTBCOKS LISTED IN THE GUIDE), AND SUGGESTIONS. THE APPENDIXCCNTAINS A FALLACIOUS PROOF, A TABLE COMPARING EUCLIDEANAND NON-EUCLIDEAN GEOMETRY, PROJECTS FORINDIVIDUAL ENRICHMENT, A GLOSSARY, AND A 64 -ITEM BIBLIOGRAPHY.RESULTS OF THE STANDARDIZED TESTS SHOWED THAT THE ACCELERATESSCORED AS WELL OR BETTER IN ALMOST ALL CASES THANTHE REGULAR CLASS PUPILS, EVEN THOUGH THE ACCELERATES WEREYOUNGER. SUBJECTIVE EVALUATION Cf ADMINISTRATION; COUNSELORS,TEACHERS, AND PUPILS SHOWED THE PROGRAM WAS HIGHLYSUCCESSFUL. (RM) AY, TEACHERS' GUIDE Ninth Grade Plane and Solid Geometry foi the Academically Talented Issued by E. E. DOLT Superintendent of Public Instruction Columbus, Ohio 1963 U.S. DEPARTMENT OF HEALTH, EDUCATION & WELFARE OFFICE OF EDUCATION THIS DOCUMENT HAS BEEN REPRODUCED EXACTLY AS RECEIVED FROM THE PERSON OR ORGANIZATION ORIGINATING IT.POINTS OF VIEW OR OPINIONS STATED DO NOT NECESSARILY REPRESENT OFFICIAL OFFICE OF EDUCATION POSITION OR POLICY. TEACHERS' GUIDE Ninth Grade Plane andSolid Geometry for the Academically Talented Prepared by CLEVELAND PUBLIC SCHOOLS Division of Mathematics In Cooperation With THE OHIO DEPARTMENT OFEDUCATION Under th,.. Direction of R. -

Proceedings of the Toulouse Global Optimization Workshop
PROCEEDINGS OF THE TOULOUSE GLOBAL OPTIMIZATION WORKSHOP Edited by S. Cafieri Ecole Nationale de l’Aviation Civile, Toulouse, France B. G.-Tóth Budapest University of Technology and Economics, Budapest, Hungary E.M.T. Hendrix University of Málaga, Málaga, Spain L. Liberti Ecole Polytechnique, Paris, France F. Messine ENSEEIHT, Toulouse, France Preface Global Optimization Workshops are organized periodically and rather spontaneously by members of the Global Optimization scientific community. Although there is no proper steer- ing committee to speak of, the tradition continues unabated ever since Szeged (Hungary 1995) and Florence (Italy, 1999) and going on to Hanmer Springs (New Zealand, 2001), Santorini (Greece, 2003), San José (Spain, 2005), Mykonos (Greece, 2007), Skukuza (South Africa, 2008). The TOulouse Global Optimization workshop (TOGO 2010) adds a new opportunity to meet on this interesting subject. In 2009 a new, larger scale format was introduced with the first World Congress of Global Optimization. Although Global Optimization is certainly mature enough to draw enough people for a congress, some of us still relish the small-scale, single-track meetings where ev- eryone gets to meet everyone else. As is customary, a special issue of the Journal of Global Optimization will be dedicated to this workshop. This year’s workshop is special in that it celebrates Pierre Hansen’s 70th birthday. Pierre has been an exceptionally important contributor to the development of Global Optimization. His works on symbolic methods for global optimization, nonlinear clustering problems, and extremal polygons all became classics in the field. He also contributed to found the related field of reformulations in mathematical programming, with a seminal paper co-signed with another one of our plenary speakers, Charles Audet. -

6-1 Properties and Attributes of Polygons Warm Up
66-1-1 PropertiesProperties andand Attributes of of Polygons Polygons Warm Up Lesson Presentation Lesson Quiz HoltHolt McDougal Geometry Geometry 6-1 Properties and Attributes of Polygons Warm Up 1. A ? is a three-sided polygon. triangle 2. A ? is a four-sided polygon. quadrilateral Evaluate each expression for n = 6. 3. (n – 4) 12 24 4. (n – 3) 90 270 Solve for a. 5. 12a + 4a + 9a = 100 4 Holt McDougal Geometry 6-1 Properties and Attributes of Polygons Objectives Classify polygons based on their sides and angles. Find and use the measures of interior and exterior angles of polygons. Holt McDougal Geometry 6-1 Properties and Attributes of Polygons Vocabulary side of a polygon vertex of a polygon diagonal regular polygon concave convex Holt McDougal Geometry 6-1 Properties and Attributes of Polygons In Lesson 2-4, you learned the definition of a polygon. Now you will learn about the parts of a polygon and about ways to classify polygons. Holt McDougal Geometry 6-1 Properties and Attributes of Polygons Each segment that forms a polygon is a side of the polygon. The common endpoint of two sides is a vertex of the polygon. A segment that connects any two nonconsecutive vertices is a diagonal. Holt McDougal Geometry 6-1 Properties and Attributes of Polygons You can name a polygon by the number of its sides. The table shows the names of some common polygons. Holt McDougal Geometry 6-1 Properties and Attributes of Polygons Remember! A polygon is a closed plane figure formed by three or more segments that intersect only at their endpoints.