DOCSLIB.ORG

Parameter Estimation

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Parameter Estimation Parameter Estimation Peter N Robinson Estimating Parameters from Data Parameter Estimation Maximum ML vs. MAP Likelihood (ML) Estimation Beta distribution Peter N Robinson Maximum a posteriori (MAP) Estimation December 14, 2012 MAQ Estimating Parameters from Data Parameter Estimation Peter N Robinson Estimating Parameters In many situations in bioinformatics, we want to estimate \op- from Data timal" parameters from data. In the examples we have seen in Maximum Likelihood the lectures on variant calling, these parameters might be the (ML) Estimation error rate for reads, the proportion of a certain genotype, the Beta proportion of nonreference bases etc. However, the hello world distribution example for this sort of thing is the coin toss, so we will start Maximum a posteriori with that. (MAP) Estimation MAQ Coin toss Parameter Estimation Peter N Robinson Estimating Parameters Let's say we have two coins that are each tossed 10 times from Data Maximum Coin 1: H,T,T,H,H,H,T,H,T,T Likelihood (ML) Coin 2: T,T,T,H,T,T,T,H,T,T Estimation Beta Intuitively, we might guess that coin one is a fair coin, i.e., distribution P(X = H) = 0:5, and that coin 2 is biased, i.e., Maximum a posteriori P(X = H) 6= 0:5 (MAP) Estimation MAQ Discrete Random Variable Parameter Estimation Peter N Let us begin to formalize this. We model the coin toss process Robinson as follows. Estimating Parameters The outcome of a single coin toss is a random variable X from Data that can take on values in a set X = fx1; x2;:::; xng Maximum Likelihood (ML) In our example, of course, n = 2, and the values are Estimation x1 = 0 (tails) and x2 = 1 (heads) Beta distribution We then have a probability mass function p : X −! [0; 1]; P Maximum a the law of total probability states that p(xi ) = 1 posteriori x2X (MAP) Estimation This is a Bernoulli distribution with parameter µ: MAQ p(X = 1; µ) = µ (1) Probability of sequence of events Parameter Estimation In general, for a sequence of two events X1 and X2, the joint Peter N probability is Robinson P(X1; X2) = p(X2jX1)p(X1) (2) Estimating Parameters Since we assume that the sequence is iid (identically and from Data independently distributed), by definition p(X2jX1) = P(X2). Maximum Likelihood Thus, for a sequence of n events (coin tosses), we have (ML) Estimation n Beta Y distribution p(x1; x2;:::; xn; µ) = p(xi ; µ) (3) Maximum a i=1 posteriori (MAP) Estimation if the probability of heads is 30%, the the probability of the MAQ sequence for coin 2 can be calculated as 3 2 7 8 p(T ; T ; T ; H; T ; T ; T ; H; T ; T ; µ) = µ2(1 − µ)8 = (4) 10 10 Probability of sequence of events Parameter Estimation Peter N Robinson Estimating Parameters Thus far, we have considered p(x; µ) as a function of x, from Data parametrized by µ. If we view p(x; µ) as a function of µ, then Maximum Likelihood it is called the likelihood function. (ML) Estimation Beta distribution Maximum a Maximum likelihood estimation basically chooses a value of µ posteriori (MAP) that maximizes the likelihood function given the observed data. Estimation MAQ Maximum likelihood for Bernoulli Parameter Estimation The likelihood for a sequence of i.i.d. Bernoulli random Peter N Robinson variables X = [x1; x2;:::; xn] with xi 2 f0; 1g is then Estimating n n Parameters Y Y xi 1−xi from Data p(X; µ) = p(xi ; µ) = µ (1 − µ) (5) Maximum i=1 i=1 Likelihood (ML) Estimation We usually maximize the log likelihood function rather than the Beta distribution original function Maximum a posteriori Often easier to take the derivative (MAP) Estimation the log function is monotonically increasing, thus, the MAQ maximum (argmax) is the same Avoid numerical problems involved with multiplying lots of small numbers Log likelihood Parameter Thus, instead of maximizing this Estimation n Peter N Y Robinson p(X; µ) = µxi (1 − µ)1−xi (6) Estimating i=1 Parameters from Data we maximize this n Maximum Likelihood Y xi 1−xi (ML) log p(X; µ) = log µ (1 − µ) Estimation i=1 Beta n distribution X = log µxi (1 − µ)1−xi Maximum a posteriori i=1 (MAP) n Estimation X xi 1−xi MAQ = log µ + log(1 − µ) i=1 n X = [xi log µ + (1 − xi ) log(1 − µ)] i=1 Log likelihood Parameter Estimation Peter N Robinson Note that one often denotes the log likelihood function with Estimating the symbol L = log p(X; µ). Parameters from Data A function f defined on a subset of the real numbers with real Maximum Likelihood values is called monotonic (also monotonically increasing, in- (ML) creasing or non-decreasing), if for all x and y such that x ≤ y Estimation Beta one has f (x) ≤ f (y) distribution Maximum a Thus, the monotonicity of the log function guarantees that posteriori (MAP) Estimation argmax p(X; µ) = argmax log p(X; µ) (7) MAQ µ µ ML estimate Parameter Estimation Peter N Robinson Estimating Parameters The ML estimate of the parameter µ is then from Data Maximum n Likelihood X (ML) argmax [xi log µ + (1 − xi ) log(1 − µ)] (8) Estimation µ i=1 Beta distribution We can calculate the argmax by setting the first derivative Maximum a posteriori equal to zero and solving for µ (MAP) Estimation MAQ ML estimate Parameter Estimation Peter N Robinson Thus Estimating Parameters n from Data @ X @ log p(X; µ) = [xi log µ + (1 − xi ) log(1 − µ)] Maximum @µ @µ Likelihood i=1 (ML) n n Estimation X @ X @ = x log µ + (1 − x ) log(1 − µ) Beta i @µ i @µ distribution i=1 i=1 Maximum a n n posteriori 1 X 1 X (MAP) = xi − (1 − xi ) Estimation µ 1 − µ i=1 i=1 MAQ ML estimate @ Parameter and finally, to find the maximum we set log p(X; µ) = 0: Estimation @µ Peter N n n Robinson 1 X 1 X 0 = xi − (1 − xi ) Estimating µ 1 − µ Parameters i=1 i=1 from Data Pn 1 − µ (1 − xi ) Maximum = i=1 Likelihood µ Pn x (ML) i=1 i Estimation Pn 1 i=1 1 Beta − 1 = Pn − 1 distribution µ i=1 xi Maximum a 1 n posteriori = n (MAP) µ P x Estimation i=1 i n MAQ 1 X µ^ = x ML n i i=1 Reassuringly, the maximum likelihood estimate is just the proportion of flips that came out heads. Problems with ML estimation Parameter Estimation Peter N Robinson Estimating Parameters Does it really make sense that from Data Maximum H,T,H,T ! µ^ = 0:5 Likelihood (ML) H,T,T,T ! µ^ = 0:25 Estimation Beta T,T,T,T! µ^ = 0:0 distribution ML estimation does not incorporate any prior knowledge and Maximum a posteriori does not generate an estimate of the certainty of its results. (MAP) Estimation MAQ Maximum a posteriori Estimation Parameter Estimation Peter N Bayesian approaches try to reflect our belief about µ. In this Robinson case, we will consider µ to be a random variable. Estimating Parameters from Data p(Xjµ)p(µ) Maximum p(µjX) = (9) Likelihood p(X) (ML) Estimation Thus, Bayes' law converts our prior belief about the parameter Beta distribution µ (before seeing data) into a posterior probability, p(µjX), by Maximum a using the likelihood function p(Xjµ). The maximum posteriori (MAP) a-posteriori (MAP) estimate is defined as Estimation MAQ µ^MAP = argmax p(µjX) (10) µ Maximum a posteriori Estimation Parameter Estimation Peter N Robinson Note that because p(X) does not depend on µ, we have Estimating Parameters from Data Maximum µ^MAP = argmax p(µjX) Likelihood µ (ML) Estimation p(Xjµ)p(µ) = argmax Beta µ p(X) distribution Maximum a = argmax p(Xjµ)p(µ) posteriori µ (MAP) Estimation This is essentially the basic idea of the MAP equation used by MAQ SNVMix for variant calling MAP Estimation; What does it buy us? Parameter Estimation To take a simple example of a situation in which MAP estima- Peter N tion might produce better results than ML estimation, let us Robinson consider a statistician who wants to predict the outcome of the Estimating Parameters next election in the USA. from Data Maximum The statistician is able to gather data on party preferences Likelihood 1 (ML) by asking people he meets at the Wall Street Golf Club Estimation which party they plan on voting for in the next election Beta distribution The statistician asks 100 people, seven of whom answer Maximum a posteriori \Democrats". This can be modeled as a series of (MAP) Estimation Bernoullis, just like the coin tosses. MAQ In this case, the maximum likelihood estimate of the proportion of voters in the USA who will vote democratic isµ ^ML = 0:07. 1i.e., a notorious haven of ultraconservative Republicans MAP Estimation; What does it buy us? Parameter Estimation Peter N Robinson Estimating Somehow, the estimate ofµ ^ML = 0:07 doesn't seem quite right Parameters given our previous experience that about half of the electorate from Data Maximum votes democratic, and half votes republican. But how should Likelihood (ML) the statistician incorporate this prior knowledge into his Estimation prediction for the next election? Beta distribution Maximum a posteriori (MAP) The MAP estimation procedure allows us to inject our prior Estimation beliefs about parameter values into the new estimate. MAQ Beta distribution: Background Parameter Estimation The Beta distribution is appropriate to express prior belief about Peter N a Bernoulli distribution.
Load more

Recommended publications
  • A Matrix-Valued Bernoulli Distribution Gianfranco Lovison1 Dipartimento Di Scienze Statistiche E Matematiche “S
    Journal of Multivariate Analysis 97 (2006) 1573–1585 www.elsevier.com/locate/jmva A matrix-valued Bernoulli distribution Gianfranco Lovison1 Dipartimento di Scienze Statistiche e Matematiche “S. Vianelli”, Università di Palermo Viale delle Scienze 90128 Palermo, Italy Received 17 September 2004 Available online 10 August 2005 Abstract Matrix-valued distributions are used in continuous multivariate analysis to model sample data matrices of continuous measurements; their use seems to be neglected for binary, or more generally categorical, data. In this paper we propose a matrix-valued Bernoulli distribution, based on the log- linear representation introduced by Cox [The analysis of multivariate binary data, Appl. Statist. 21 (1972) 113–120] for the Multivariate Bernoulli distribution with correlated components. © 2005 Elsevier Inc. All rights reserved. AMS 1991 subject classification: 62E05; 62Hxx Keywords: Correlated multivariate binary responses; Multivariate Bernoulli distribution; Matrix-valued distributions 1. Introduction Matrix-valued distributions are used in continuous multivariate analysis (see, for exam- ple, [10]) to model sample data matrices of continuous measurements, allowing for both variable-dependence and unit-dependence. Their potentials seem to have been neglected for binary, and more generally categorical, data. This is somewhat surprising, since the natural, elementary representation of datasets with categorical variables is precisely in the form of sample binary data matrices, through the 0-1 coding of categories. E-mail address: [email protected] URL: http://dssm.unipa.it/lovison. 1 Work supported by MIUR 60% 2000, 2001 and MIUR P.R.I.N. 2002 grants. 0047-259X/$ - see front matter © 2005 Elsevier Inc. All rights reserved. doi:10.1016/j.jmva.2005.06.008 1574 G.
    [Show full text]
  • Discrete Probability Distributions Uniform Distribution Bernoulli
    Discrete Probability Distributions Uniform Distribution Experiment obeys: all outcomes equally probable Random variable: outcome Probability distribution: if k is the number of possible outcomes, 1 if x is a possible outcome p(x)= k ( 0 otherwise Example: tossing a fair die (k = 6) Bernoulli Distribution Experiment obeys: (1) a single trial with two possible outcomes (success and failure) (2) P trial is successful = p Random variable: number of successful trials (zero or one) Probability distribution: p(x)= px(1 − p)n−x Mean and variance: µ = p, σ2 = p(1 − p) Example: tossing a fair coin once Binomial Distribution Experiment obeys: (1) n repeated trials (2) each trial has two possible outcomes (success and failure) (3) P ith trial is successful = p for all i (4) the trials are independent Random variable: number of successful trials n x n−x Probability distribution: b(x; n,p)= x p (1 − p) Mean and variance: µ = np, σ2 = np(1 − p) Example: tossing a fair coin n times Approximations: (1) b(x; n,p) ≈ p(x; λ = pn) if p ≪ 1, x ≪ n (Poisson approximation) (2) b(x; n,p) ≈ n(x; µ = pn,σ = np(1 − p) ) if np ≫ 1, n(1 − p) ≫ 1 (Normal approximation) p Geometric Distribution Experiment obeys: (1) indeterminate number of repeated trials (2) each trial has two possible outcomes (success and failure) (3) P ith trial is successful = p for all i (4) the trials are independent Random variable: trial number of first successful trial Probability distribution: p(x)= p(1 − p)x−1 1 2 1−p Mean and variance: µ = p , σ = p2 Example: repeated attempts to start
    [Show full text]
  • STATS8: Introduction to Biostatistics 24Pt Random Variables And
    STATS8: Introduction to Biostatistics Random Variables and Probability Distributions Babak Shahbaba Department of Statistics, UCI Random variables • In this lecture, we will discuss random variables and their probability distributions. • Formally, a random variable X assigns a numerical value to each possible outcome (and event) of a random phenomenon. • For instance, we can define X based on possible genotypes of a bi-allelic gene A as follows: 8 < 0 for genotype AA; X = 1 for genotype Aa; : 2 for genotype aa: • Alternatively, we can define a random, Y , variable this way: 0 for genotypes AA and aa; Y = 1 for genotype Aa: Random variables • After we define a random variable, we can find the probabilities for its possible values based on the probabilities for its underlying random phenomenon. • This way, instead of talking about the probabilities for different outcomes and events, we can talk about the probability of different values for a random variable. • For example, suppose P(AA) = 0:49, P(Aa) = 0:42, and P(aa) = 0:09. • Then, we can say that P(X = 0) = 0:49, i.e., X is equal to 0 with probability of 0.49. • Note that the total probability for the random variable is still 1. Random variables • The probability distribution of a random variable specifies its possible values (i.e., its range) and their corresponding probabilities. • For the random variable X defined based on genotypes, the probability distribution can be simply specified as follows: 8 < 0:49 for x = 0; P(X = x) = 0:42 for x = 1; : 0:09 for x = 2: Here, x denotes a specific value (i.e., 0, 1, or 2) of the random variable.
    [Show full text]
  • Chapter 5 Sections
    Chapter 5 Chapter 5 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions Continuous univariate distributions: 5.6 Normal distributions 5.7 Gamma distributions Just skim 5.8 Beta distributions Multivariate distributions Just skim 5.9 Multinomial distributions 5.10 Bivariate normal distributions 1 / 43 Chapter 5 5.1 Introduction Families of distributions How: Parameter and Parameter space pf /pdf and cdf - new notation: f (xj parameters ) Mean, variance and the m.g.f. (t) Features, connections to other distributions, approximation Reasoning behind a distribution Why: Natural justification for certain experiments A model for the uncertainty in an experiment All models are wrong, but some are useful – George Box 2 / 43 Chapter 5 5.2 Bernoulli and Binomial distributions Bernoulli distributions Def: Bernoulli distributions – Bernoulli(p) A r.v. X has the Bernoulli distribution with parameter p if P(X = 1) = p and P(X = 0) = 1 − p. The pf of X is px (1 − p)1−x for x = 0; 1 f (xjp) = 0 otherwise Parameter space: p 2 [0; 1] In an experiment with only two possible outcomes, “success” and “failure”, let X = number successes. Then X ∼ Bernoulli(p) where p is the probability of success. E(X) = p, Var(X) = p(1 − p) and (t) = E(etX ) = pet + (1 − p) 8 < 0 for x < 0 The cdf is F(xjp) = 1 − p for 0 ≤ x < 1 : 1 for x ≥ 1 3 / 43 Chapter 5 5.2 Bernoulli and Binomial distributions Binomial distributions Def: Binomial distributions – Binomial(n; p) A r.v.
    [Show full text]
  • Lecture 6: Special Probability Distributions
    The Discrete Uniform Distribution The Bernoulli Distribution The Binomial Distribution The Negative Binomial and Geometric Di Lecture 6: Special Probability Distributions Assist. Prof. Dr. Emel YAVUZ DUMAN MCB1007 Introduction to Probability and Statistics Istanbul˙ K¨ult¨ur University The Discrete Uniform Distribution The Bernoulli Distribution The Binomial Distribution The Negative Binomial and Geometric Di Outline 1 The Discrete Uniform Distribution 2 The Bernoulli Distribution 3 The Binomial Distribution 4 The Negative Binomial and Geometric Distribution The Discrete Uniform Distribution The Bernoulli Distribution The Binomial Distribution The Negative Binomial and Geometric Di Outline 1 The Discrete Uniform Distribution 2 The Bernoulli Distribution 3 The Binomial Distribution 4 The Negative Binomial and Geometric Distribution The Discrete Uniform Distribution The Bernoulli Distribution The Binomial Distribution The Negative Binomial and Geometric Di The Discrete Uniform Distribution If a random variable can take on k different values with equal probability, we say that it has a discrete uniform distribution; symbolically, Definition 1 A random variable X has a discrete uniform distribution and it is referred to as a discrete uniform random variable if and only if its probability distribution is given by 1 f (x)= for x = x , x , ··· , xk k 1 2 where xi = xj when i = j. The Discrete Uniform Distribution The Bernoulli Distribution The Binomial Distribution The Negative Binomial and Geometric Di The mean and the variance of this distribution are Mean: k k 1 x1 + x2 + ···+ xk μ = E[X ]= xi f (xi ) = xi · = , k k i=1 i=1 1/k Variance: k 2 2 2 1 σ = E[(X − μ) ]= (xi − μ) · k i=1 2 2 2 (x − μ) +(x − μ) + ···+(xk − μ) = 1 2 k The Discrete Uniform Distribution The Bernoulli Distribution The Binomial Distribution The Negative Binomial and Geometric Di In the special case where xi = i, the discrete uniform distribution 1 becomes f (x)= k for x =1, 2, ··· , k, and in this from it applies, for example, to the number of points we roll with a balanced die.
    [Show full text]
  • 11. Parameter Estimation
    11. Parameter Estimation Chris Piech and Mehran Sahami May 2017 We have learned many different distributions for random variables and all of those distributions had parame- ters: the numbers that you provide as input when you define a random variable. So far when we were working with random variables, we either were explicitly told the values of the parameters, or, we could divine the values by understanding the process that was generating the random variables. What if we don’t know the values of the parameters and we can’t estimate them from our own expert knowl- edge? What if instead of knowing the random variables, we have a lot of examples of data generated with the same underlying distribution? In this chapter we are going to learn formal ways of estimating parameters from data. These ideas are critical for artificial intelligence. Almost all modern machine learning algorithms work like this: (1) specify a probabilistic model that has parameters. (2) Learn the value of those parameters from data. Parameters Before we dive into parameter estimation, first let’s revisit the concept of parameters. Given a model, the parameters are the numbers that yield the actual distribution. In the case of a Bernoulli random variable, the single parameter was the value p. In the case of a Uniform random variable, the parameters are the a and b values that define the min and max value. Here is a list of random variables and the corresponding parameters. From now on, we are going to use the notation q to be a vector of all the parameters: Distribution Parameters Bernoulli(p) q = p Poisson(l) q = l Uniform(a,b) q = (a;b) Normal(m;s 2) q = (m;s 2) Y = mX + b q = (m;b) In the real world often you don’t know the “true” parameters, but you get to observe data.
    [Show full text]
  • Chapter 3. Discrete Random Variables and Probability Distributions
    Chapter 3. Discrete random variables and probability distributions. ::::Defn: A :::::::random::::::::variable (r.v.) is a function that takes a sample point in S and maps it to it a real number. That is, a r.v. Y maps the sample space (its domain) to the real number line (its range), Y : S ! R. ::::::::Example: In an experiment, we roll two dice. Let the r.v. Y = the sum of two dice. The r.v. Y as a function: (1; 1) ! 2 (1; 2) ! 3 . (6; 6) ! 12 Discrete random variables and their distributions ::::Defn: A :::::::discrete::::::::random :::::::variable is a r.v. that takes on a ::::finite or :::::::::countably ::::::infinite number of different values. ::::Defn: The probability mass function (pmf) of a discrete r.v Y is a function that maps each possible value of Y to its probability. (It is also called the probability distribution of a discrete r.v. Y ). pY : Range(Y ) ! [0; 1]: pY (v) = P(Y = v), where ‘Y=v’ denotes the event f! : Y (!) = vg. ::::::::Notation: We use capital letters (like Y ) to denote a random variable, and a lowercase letters (like v) to denote a particular value the r.v. may take. Cumulative distribution function ::::Defn: The cumulative distribution function (cdf) is defined as F(v) = P(Y ≤ v): pY : Range(Y ) ! [0; 1]: Example: We toss two fair coins. Let Y be the number of heads. What is the pmf of Y ? What is the cdf? Quiz X a random variable. values of X: 1 3 5 7 cdf F(a): .5 .75 .9 1 What is P(X ≤ 3)? (A) .15 (B) .25 (C) .5 (D) .75 Quiz X a random variable.
    [Show full text]
  • Some Discrete Distributions.Pdf
    CHAPTER 6 Some discrete distributions 6.1. Examples: Bernoulli, binomial, Poisson, geometric distributions Bernoulli distribution A random variable X such that P(X = 1) = p and P(X = 0) = 1 − p is said to be a Bernoulli random variable with parameter p. Note EX = p and EX2 = p, so Var X = p − p2 = p(1 − p). We denote such a random variable by X ∼ Bern (p). Binomial distribution A random variable X has a binomial distribution with parameters n and p if P(X = n k n−k. k) = k p (1 − p) We denote such a random variable by X ∼ Binom (n; p). The number of successes in n Bernoulli trials is a binomial random variable. After some cumbersome calculations one can derive EX = np. An easier way is to realize that if X is binomial, then X = Y1 + ··· + Yn, where the Yi are independent Bernoulli variables, so . EX = EY1 + ··· + EYn = np We have not dened yet what it means for random variables to be independent, but here we mean that the events such as (Yi = 1) are independent. Proposition 6.1 Suppose , where n are independent Bernoulli random variables X := Y1 +···+Yn fYigi=1 with parameter p, then EX = np; Var X = np(1 − p): Proof. First we use the denition of expectation to see that n n X n X n X = i pi(1 − p)n−i = i pi(1 − p)n−i: E i i i=0 i=1 Then 81 82 6. SOME DISCRETE DISTRIBUTIONS n X n! X = i pi(1 − p)n−i E i!(n − i)! i=1 n X (n − 1)! = np pi−1(1 − p)(n−1)−(i−1) (i − 1)!((n − 1) − (i − 1))! i=1 n−1 X (n − 1)! = np pi(1 − p)(n−1)−i i!((n − 1) − i)! i=0 n−1 X n − 1 = np pi(1 − p)(n−1)−i = np; i i=0 where we used the Binomial Theorem (Theorem 1.1).
    [Show full text]
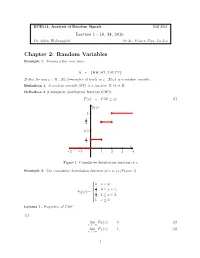
  • Chapter 2: Random Variables Example 1
    ECE511: Analysis of Random Signals Fall 2016 Lecture 1 - 10, 24, 2016 Dr. Salim El Rouayheb Scribe: Peiwen Tian, Lu Liu Chapter 2: Random Variables Example 1. Tossing a fair coin twice: Ω = fHH;HT;TH;TT g: Define for any ! 2 Ω , X(!)=number of heads in !. X(!) is a random variable. Definition 1. A random variable (RV) is a function X: Ω ! R. Definition 2 (Cumulative distribution function(CDF)). F (χ) = P (X ≤ χ): (1) F(x) 1 3 4 0:5 1 4 x −2 −1 1 2 3 4 . Figure 1: Cumulative distribution function of x Example 2. The cumulative distribution function of x is as (Figure 1) 8 > >0 x < 0; <> 1 0 ≤ x < 1; F (x) = 4 X > 3 > 1 ≤ x < 2; :> 4 1 x ≥ 2: Lemma 1. Properties of CDF (1) lim FX (x) = 0 (2) x→−∞ lim FX (x) = 1; (3) x!+1 1 (2) FX (x) is non-decreasing: x1 ≤ x2 =) FX (x1) ≤ FX (x2) (4) (3) FX (x)is continuous from the right lim FX (x + ϵ) = FX (x); ϵ > 0 (5) ϵ!0 (4) P (a ≤ X ≤ b) = P (X ≤ b) − P (X ≤ a) + P (X = a) (6) = FX (b) − FX (a) + P (X = a) (7) (5) P (X = a) = lim FX (a) − FX (a − "); " > 0 (8) "!0 Definition 3. If random variable X has finite or countable number of values, X is called discrete. Example 3. Non-countable example:<: A set S is countable if you can find a bijection of f. f : S ! N: Definition 4. X is continuous if FX (x) is continuous.
    [Show full text]
  • Discrete Distributions: Empirical, Bernoulli, Binomial, Poisson
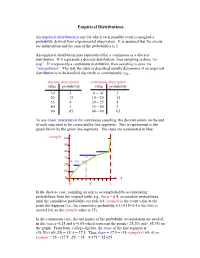
    Empirical Distributions An empirical distribution is one for which each possible event is assigned a probability derived from experimental observation. It is assumed that the events are independent and the sum of the probabilities is 1. An empirical distribution may represent either a continuous or a discrete distribution. If it represents a discrete distribution, then sampling is done “on step”. If it represents a continuous distribution, then sampling is done via “interpolation”. The way the table is described usually determines if an empirical distribution is to be handled discretely or continuously; e.g., discrete description continuous description value probability value probability 10 .1 0 – 10- .1 20 .15 10 – 20- .15 35 .4 20 – 35- .4 40 .3 35 – 40- .3 60 .05 40 – 60- .05 To use linear interpolation for continuous sampling, the discrete points on the end of each step need to be connected by line segments. This is represented in the graph below by the green line segments. The steps are represented in blue: rsample 60 50 40 30 20 10 0 x 0 .5 1 In the discrete case, sampling on step is accomplished by accumulating probabilities from the original table; e.g., for x = 0.4, accumulate probabilities until the cumulative probability exceeds 0.4; rsample is the event value at the point this happens (i.e., the cumulative probability 0.1+0.15+0.4 is the first to exceed 0.4, so the rsample value is 35). In the continuous case, the end points of the probability accumulation are needed, in this case x=0.25 and x=0.65 which represent the points (.25,20) and (.65,35) on the graph.
    [Show full text]
  • Hand-Book on STATISTICAL DISTRIBUTIONS for Experimentalists
    Internal Report SUF–PFY/96–01 Stockholm, 11 December 1996 1st revision, 31 October 1998 last modification 10 September 2007 Hand-book on STATISTICAL DISTRIBUTIONS for experimentalists by Christian Walck Particle Physics Group Fysikum University of Stockholm (e-mail: [email protected]) Contents 1 Introduction 1 1.1 Random Number Generation .............................. 1 2 Probability Density Functions 3 2.1 Introduction ........................................ 3 2.2 Moments ......................................... 3 2.2.1 Errors of Moments ................................ 4 2.3 Characteristic Function ................................. 4 2.4 Probability Generating Function ............................ 5 2.5 Cumulants ......................................... 6 2.6 Random Number Generation .............................. 7 2.6.1 Cumulative Technique .............................. 7 2.6.2 Accept-Reject technique ............................. 7 2.6.3 Composition Techniques ............................. 8 2.7 Multivariate Distributions ................................ 9 2.7.1 Multivariate Moments .............................. 9 2.7.2 Errors of Bivariate Moments .......................... 9 2.7.3 Joint Characteristic Function .......................... 10 2.7.4 Random Number Generation .......................... 11 3 Bernoulli Distribution 12 3.1 Introduction ........................................ 12 3.2 Relation to Other Distributions ............................. 12 4 Beta distribution 13 4.1 Introduction .......................................
    [Show full text]
  • Discrete Probability Distributions
    Machine Learning Srihari Discrete Probability Distributions Sargur N. Srihari 1 Machine Learning Srihari Binary Variables Bernoulli, Binomial and Beta 2 Machine Learning Srihari Bernoulli Distribution • Expresses distribution of Single binary-valued random variable x ε {0,1} • Probability of x=1 is denoted by parameter µ, i.e., p(x=1|µ)=µ – Therefore p(x=0|µ)=1-µ • Probability distribution has the form Bern(x|µ)=µ x (1-µ) 1-x • Mean is shown to be E[x]=µ Jacob Bernoulli • Variance is var[x]=µ (1-µ) 1654-1705 • Likelihood of n observations independently drawn from p(x|µ) is N N x 1−x p(D | ) = p(x | ) = n (1− ) n µ ∏ n µ ∏µ µ n=1 n=1 – Log-likelihood is N N ln p(D | ) = ln p(x | ) = {x ln +(1−x )ln(1− )} µ ∑ n µ ∑ n µ n µ n=1 n=1 • Maximum likelihood estimator 1 N – obtained by setting derivative of ln p(D|µ) wrt m equal to zero is = x µML ∑ n N n=1 • If no of observations of x=1 is m then µML=m/N 3 Machine Learning Srihari Binomial Distribution • Related to Bernoulli distribution • Expresses Distribution of m – No of observations for which x=1 • It is proportional to Bern(x|µ) Histogram of Binomial for • Add up all ways of obtaining heads N=10 and ⎛ ⎞ m=0.25 ⎜ N ⎟ m N−m Bin(m | N,µ) = ⎜ ⎟µ (1− µ) ⎝⎜ m ⎠⎟ Binomial Coefficients: ⎛ ⎞ N ! ⎜ N ⎟ • Mean and Variance are ⎜ ⎟ = ⎝⎜ m ⎠⎟ m!(N −m)! N E[m] = ∑mBin(m | N,µ) = Nµ m=0 Var[m] = N (1− ) 4 µ µ Machine Learning Srihari Beta Distribution • Beta distribution a=0.1, b=0.1 a=1, b=1 Γ(a + b) Beta(µ |a,b) = µa−1(1 − µ)b−1 Γ(a)Γ(b) • Where the Gamma function is defined as ∞ Γ(x) = ∫u x−1e−u du
    [Show full text]