Incorporating Topological and Age Uncertainty Into Event-Based Biogeography of Sand Spiders Supports Paleo-Islands in Galapago
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

A Checklist of the Non -Acarine Arachnids
Original Research A CHECKLIST OF THE NON -A C A RINE A R A CHNIDS (CHELICER A T A : AR A CHNID A ) OF THE DE HOOP NA TURE RESERVE , WESTERN CA PE PROVINCE , SOUTH AFRIC A Authors: ABSTRACT Charles R. Haddad1 As part of the South African National Survey of Arachnida (SANSA) in conserved areas, arachnids Ansie S. Dippenaar- were collected in the De Hoop Nature Reserve in the Western Cape Province, South Africa. The Schoeman2 survey was carried out between 1999 and 2007, and consisted of five intensive surveys between Affiliations: two and 12 days in duration. Arachnids were sampled in five broad habitat types, namely fynbos, 1Department of Zoology & wetlands, i.e. De Hoop Vlei, Eucalyptus plantations at Potberg and Cupido’s Kraal, coastal dunes Entomology University of near Koppie Alleen and the intertidal zone at Koppie Alleen. A total of 274 species representing the Free State, five orders, 65 families and 191 determined genera were collected, of which spiders (Araneae) South Africa were the dominant taxon (252 spp., 174 genera, 53 families). The most species rich families collected were the Salticidae (32 spp.), Thomisidae (26 spp.), Gnaphosidae (21 spp.), Araneidae (18 2 Biosystematics: spp.), Theridiidae (16 spp.) and Corinnidae (15 spp.). Notes are provided on the most commonly Arachnology collected arachnids in each habitat. ARC - Plant Protection Research Institute Conservation implications: This study provides valuable baseline data on arachnids conserved South Africa in De Hoop Nature Reserve, which can be used for future assessments of habitat transformation, 2Department of Zoology & alien invasive species and climate change on arachnid biodiversity. -
World Bank Document
GLOBAL ENVIRONMENT 33977 FACILITY Public Disclosure Authorized Public Disclosure Authorized Quarterly Operational Report April 1995 Public Disclosure Authorized GEF Public Disclosure Authorized development,agencies, national institutions, (GEF) is a financial tions, bilateral T mechanismhe Global Environment that provides Facility grant and concessional funds non-governmental organizations (NGOs), private sector to developing countries for projects and activities that aim entities, and academic institutions. The GEF also comprises to protect the global environment. GEF resources are avail- a Small Grants Programme available for projects in the able for projects and other activities that address climate four focal areas that are put forward by grassroots groups change, loss of biological diversity, pollution of international and NGOs in developing countries. waters, and depletion of the ozone layer. Countries can The Quarterly Operational Report is designed to pro- obtain GEF funds if they are eligible to borrow from the vide a comprehensive review of, and a status report on, the World Bank (IBRD and/or IDA) or receive technical assis- GEE work program. A brief description of each of the GEE's tance grants from UNDP through a country program. projects organized alphabetically by region can be Responsibility for implementing GEF activities is found on pages 8-J8. Each description lists the name of the shared by the United Nations Development Programme UNDP, UNEP or World Bank Task Manager responsible for (UNDP), the United Nations Environment Programme the project. Inquiries about specific projects should be (UNEP) and the World Bank. UNDP is responsible for referred to the responsible Task Manager. Their telephone technical assistance activities, capacity building, and the and fax numbers can be found on pages 63 and 64. -

On Some New Species of Spiders of the Family Oxyopidae from India
ON SOME NEW SPECIES OF SPIDERS OF THE FAMILY OXYOPIDAE FROM INDIA BY B. K. TIKADEK (Zoological Survey of India, Western Regional Station, Poona) Received February 8, 1965 (Communicated by Prof. T. S. Mahabale, F.A.SC.) INTRODUCTION SPIDERS of the family Oxyopidae have received scant attention in India. Since Pocock's classical work (1900) on the Indian Arachnida no serious attention has been given to explore the spider fauna of this country. Even this representative work contains no adequate references to such an obscure family as Oxyopidae. Only Pocock (1901) described four new species of the genus Oxyopes. But the genus Peucetia is practically unknown from our country. Recently Brady (1964) has described a number of species of the family Oxyopidae from North America. While examining the spider collection from Maharashtra, I came across three new species of spiders of the genera Oxyopes and Peucetia, which are described in tiffs paper. The type specimens will in due course be deposited in the collection of the Zoological Survey of India, Calcutta. 1. Oxyopes chittrae sp. nov. General.--Cephalothorax and legs brownish-green, abdomen brown. Total length 6.90 mm. Carapace 2.50 mm. long, 1-50 mm. wide; abdomen 4.20mm. long, 2.40mm. wide. Cephalothorax.--Longer than wide, high, narrowing in front, cephalic region slightly high, clothed with fine hairs; centre of thorax provided with fine fovea. Eyes black, and bases encircled with back patch. Posterior row procurved and situated in equal distance; anterior row strongly re- curved and anterior mediar/eyes smaller than others. Clypeus long. Ster- num heart-shaped, pointed behind, clothed with hairs. -
Oxyopes Sitae Tikader but ~Iffers from It As Follows: (I) Clypeus Provided with Chalk White Patch but in Oxyopes Sitae Clypeus Provided with Two Black Lines
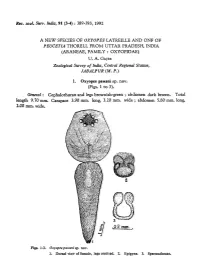
Ree. zool. Surv. India, 91 (3-4) : 389-393, 1992 A NEW SPECIES OF OXYOPES LATREILLE AND ONF OF PEUCETIA THORELL FROM UTTAR PRADESH, INDIA (ARANEAE, FAMILY: OXYOPIDAE) U. A. GAJBE Zoological Survey of India, CentTal Regional Station, JABALPUR (M. P.) 1. Oxyopes paw8ni sp. nov. (Figs. 1 to 3). General: Cephalothorax and legs brownish-green; abdomen dark brown. Total length 9.70 mm. Carapace 3.90 mm. long, 3.20 mm. wide; abdomen 5.80 mm. long, 2.00 mm. wide. Figs. 1-3. Oxyopespawani sp. nov. 1. Dorsal view of female, legs omitted. 2. Epigyne. 3. Spermathecae. 390 Records of the Zoological Survey of India Cephalothorax: Longer than wide, convex, with cephalic region high and broad, clothed with white pubescence; posterior half proveded with conspicuous fovea. Anterior row of eyes strongly recurved (as seen from in front), with medians smaller than laterals, and with eyes equally spaced; posterior row of eyes procurved, with eyes equal in size and equidistand from each other; all eyes encircled with black patch. Clypeus long, provided with chalk-white patch extending from anterior median eyes to near base of fang of chelicerae. Chelicerae moderately strong; inner margin provi4ed with one small tooth and outer margin with two dissimilar teeth. Labium and maxillae" longer than wide, brownish green; maxillae provided with scopula. Sternum heart shaped, pointed behind, provided with hairs and some short spines. Legs relatively long and strong, clothed with hairs and conspicuous long spines. Abdomen: Long, narrowing behind, clothed with white pubescence and muscular corrugations as in text-fig. 1 ; ventral side provided with midventral black patch and two longitudinal white patches extending from epigastric furrow to base of spinnerets. -

A Multilocus Phylogeny of Podoctidae
Molecular Phylogenetics and Evolution 106 (2017) 164–173 Contents lists available at ScienceDirect Molecular Phylogenetics and Evolution journal homepage: www.elsevier.com/locate/ympev A multilocus phylogeny of Podoctidae (Arachnida, Opiliones, Laniatores) and parametric shape analysis reveal the disutility of subfamilial nomenclature in armored harvestman systematics ⇑ Prashant P. Sharma a, , Marc A. Santiago b, Ricardo Kriebel c, Savana M. Lipps a, Perry A.C. Buenavente d, Arvin C. Diesmos d, Milan Janda e,f, Sarah L. Boyer g, Ronald M. Clouse b, Ward C. Wheeler b a Department of Zoology, University of Wisconsin-Madison, 430 Lincoln Drive, Madison, WI 53706, USA b Division of Invertebrate Zoology, American Museum of Natural History, Central Park West at 79th Street, New York, NY, 10024, USA c Department of Botany, University of Wisconsin-Madison, 430 Lincoln Drive, Madison, WI 53706, USA d Zoology Division, National Museum of the Philippines, Padre Burgos Avenue, Ermita 1000, Manila, Philippines e Laboratorio Nacional de Análisis y Síntesis Ecológica, ENES, UNAM, Antigua Carretera a Pátzcuaro, 8701 Morelia, Mexico f Biology Centre, Czech Academy of Sciences, Branisovska 31, 370 05 Ceske Budejovice, Czech Republic g Biology Department, Macalester College, 1600 Grand Avenue, St. Paul, MN 55105, USA article info abstract Article history: The taxonomy and systematics of the armored harvestmen (suborder Laniatores) are based on various Received 9 August 2016 sets of morphological characters pertaining to shape, armature, pedipalpal setation, and the number of Accepted 20 September 2016 articles of the walking leg tarsi. Few studies have tested the validity of these historical character systems Available online 21 September 2016 in a comprehensive way, with reference to an independent data class, i.e., molecular sequence data. -

Hull) Mphil (Cantab)
Thesis submitted for the degree of Doctor of Philosophy At the University of Leicester By William D. Gosling BSc (Hull) MPhil (Cantab) Department of Geography University of Leicester Submitted: December 2003 Examined: April 2004 © William This thesis is copyright material and no quotation from it may be published without proper UMI Number: U188605 All rights reserved INFORMATION TO ALL USERS The quality of this reproduction is dependent upon the quality of the copy submitted. In the unlikely event that the author did not send a complete manuscript and there are missing pages, these will be noted. Also, if material had to be removed, a note will indicate the deletion. Dissertation Publishing UMI U188605 Published by ProQuest LLC 2014. Copyright in the Dissertation held by the Author. Microform Edition © ProQuest LLC. All rights reserved. This work is protected against unauthorized copying under Title 17, United States Code. ProQuest LLC 789 East Eisenhower Parkway P.O. Box 1346 Ann Arbor, Ml 48106-1346 Characterization of Neotropical forest and savannah ecosystems by their modern pollen spectra William D. Gosling Abstract Controversy surrounds the Quaternary palaeoenvironmental history of Amazonia. It is unclear whether moist evergreen forest, savannah or seasonally dry forest dominated the Amazon basin at the last glacial maximum (c. 21,000 years B.P.). In part the uncertainty surrounding the palaeoenvironmental history of Amazonia stems from a poor understanding of the ecological significance of the fossil pollen records from the region. In order to improve interpretations of the fossil pollen record it is essential to better understand the nature of the pollen rain produced by modem ecosystems. -

The Effects of Forest-Savanna-Grassland Gradients on Bird Communities of Chiquitano Dry Forests Domain, in Western Brazil
Anais da Academia Brasileira de Ciências ISSN: 0001-3765 [email protected] Academia Brasileira de Ciências Brasil GODOI, MAURICIO N.; DE SOUZA, EDIVALDO O. The effects of forest-savanna-grassland gradients on bird communities of Chiquitano Dry Forests domain, in western Brazil Anais da Academia Brasileira de Ciências, vol. 88, núm. 3, 2016, pp. 1755-1767 Academia Brasileira de Ciências Rio de Janeiro, Brasil Available in: http://www.redalyc.org/articulo.oa?id=32748476014 How to cite Complete issue Scientific Information System More information about this article Network of Scientific Journals from Latin America, the Caribbean, Spain and Portugal Journal's homepage in redalyc.org Non-profit academic project, developed under the open access initiative Anais da Academia Brasileira de Ciências (2016) 88(3 Suppl.): 1755-1767 (Annals of the Brazilian Academy of Sciences) Printed version ISSN 0001-3765 / Online version ISSN 1678-2690 http://dx.doi.org/10.1590/0001-3765201620150615 www.scielo.br/aabc The effects of forest-savanna-grassland gradients on bird communities of Chiquitano Dry Forests domain, in western Brazil MAURICIO N. GODOI1 and EDIVALDO O. DE SOUZA2 1Programa de Pós-Graduação em Ecologia e Conservação, Centro de Ciências Biológicas e da Saúde, Universidade Federal de Mato Grosso do Sul, Cidade Universitária, s/n, 79070-900 Campo Grande, MS, Brasil 2Departamento de Biologia, Universidade Federal de Mato Grosso do Sul/UFMS, Campus Universitário de Aquidauana, CPAQ, Avenida Oscar Trindade de Barros, 740, Unidade II, Serraria, 79200-000 Aquidauana, MS, Brasil Manuscript received on August 27, 2015; accepted for publication on December 7, 2015 ABSTRACT Different vegetation types are distributed in mountains according to altitude, topography and soil. -

Sphingomyelinase D Activity in Sicarius Tropicus Venom:Toxic
toxins Article Sphingomyelinase D Activity in Sicarius tropicus Venom: Toxic Potential and Clues to the Evolution of SMases D in the Sicariidae Family Priscila Hess Lopes 1, Caroline Sayuri Fukushima 2,3 , Rosana Shoji 1, Rogério Bertani 2 and Denise V. Tambourgi 1,* 1 Immunochemistry Laboratory, Butantan Institute, São Paulo 05503-900, Brazil; [email protected] (P.H.L.); [email protected] (R.S.) 2 Special Laboratory of Ecology and Evolution, Butantan Institute, São Paulo 05503-900, Brazil; [email protected] (C.S.F.); [email protected] (R.B.) 3 Finnish Museum of Natural History, University of Helsinki, 00014 Helsinki, Finland * Correspondence: [email protected] Abstract: The spider family Sicariidae includes three genera, Hexophthalma, Sicarius and Loxosceles. The three genera share a common characteristic in their venoms: the presence of Sphingomyelinases D (SMase D). SMases D are considered the toxins that cause the main pathological effects of the Loxosceles venom, that is, those responsible for the development of loxoscelism. Some studies have shown that Sicarius spiders have less or undetectable SMase D activity in their venoms, when compared to Hexophthalma. In contrast, our group has shown that Sicarius ornatus, a Brazilian species, has active SMase D and toxic potential to envenomation. However, few species of Sicarius have been characterized for their toxic potential. In order to contribute to a better understanding about the toxicity of Sicarius venoms, the aim of this study was to characterize the toxic properties of male and female venoms from Sicarius tropicus and compare them with that from Loxosceles laeta, one Citation: Lopes, P.H.; Fukushima, of the most toxic Loxosceles venoms. -

Selection for Imperfection: a Review of Asymmetric Genitalia 2 in Araneomorph Spiders (Araneae: Araneomorphae)
bioRxiv preprint doi: https://doi.org/10.1101/704692; this version posted July 16, 2019. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY 4.0 International license. 1 Selection for imperfection: A review of asymmetric genitalia 2 in araneomorph spiders (Araneae: Araneomorphae). 3 4 5 6 F. ANDRES RIVERA-QUIROZ*1, 3, MENNO SCHILTHUIZEN2, 3, BOOPA 7 PETCHARAD4 and JEREMY A. MILLER1 8 1 Department Biodiversity Discovery group, Naturalis Biodiversity Center, 9 Darwinweg 2, 2333CR Leiden, The Netherlands 10 2 Endless Forms Group, Naturalis Biodiversity Center, Darwinweg 2, 2333CR Leiden, 11 The Netherlands 12 3 Institute for Biology Leiden (IBL), Leiden University, Sylviusweg 72, 2333BE 13 Leiden, The Netherlands. 14 4 Faculty of Science and Technology, Thammasat University, Rangsit, Pathum Thani, 15 12121 Thailand. 16 17 18 19 Running Title: Asymmetric genitalia in spiders 20 21 *Corresponding author 22 E-mail: [email protected] (AR) 23 bioRxiv preprint doi: https://doi.org/10.1101/704692; this version posted July 16, 2019. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY 4.0 International license. 24 Abstract 25 26 Bilateral asymmetry in the genitalia is a rare but widely dispersed phenomenon in the 27 animal tree of life. In arthropods, occurrences vary greatly from one group to another 28 and there seems to be no common explanation for all the independent origins. -

Loxosceles Laeta (Nicolet) (Arachnida: Araneae) in Southern Patagonia
Revista de la Sociedad Entomológica Argentina ISSN: 0373-5680 ISSN: 1851-7471 [email protected] Sociedad Entomológica Argentina Argentina The recent expansion of Chilean recluse Loxosceles laeta (Nicolet) (Arachnida: Araneae) in Southern Patagonia Faúndez, Eduardo I.; Alvarez-Muñoz, Claudia X.; Carvajal, Mariom A.; Vargas, Catalina J. The recent expansion of Chilean recluse Loxosceles laeta (Nicolet) (Arachnida: Araneae) in Southern Patagonia Revista de la Sociedad Entomológica Argentina, vol. 79, no. 2, 2020 Sociedad Entomológica Argentina, Argentina Available in: https://www.redalyc.org/articulo.oa?id=322062959008 PDF generated from XML JATS4R by Redalyc Project academic non-profit, developed under the open access initiative Notas e recent expansion of Chilean recluse Loxosceles laeta (Nicolet) (Arachnida: Araneae) in Southern Patagonia La reciente expansión de Loxosceles laeta (Nicolet) (Arachnida: Araneae) en la Patagonia Austral Eduardo I. Faúndez Laboratorio de entomología, Instituto de la Patagonia, Universidad de Magallanes, Chile Claudia X. Alvarez-Muñoz Unidad de zoonosis, Secretaria Regional Ministerial de Salud de Aysén, Chile Mariom A. Carvajal [email protected] Laboratorio de entomología, Instituto de la Patagonia, Universidad de Magallanes, Chile Catalina J. Vargas Revista de la Sociedad Entomológica Argentina, vol. 79, no. 2, 2020 Laboratorio de entomología, Instituto de la Patagonia, Universidad de Sociedad Entomológica Argentina, Magallanes, Chile Argentina Received: 06 February 2020 Accepted: 03 May 2020 Published: 29 June 2020 Abstract: e recent expansion of the Chilean recluse Loxosceles laeta (Nicolet, 1849) Redalyc: https://www.redalyc.org/ in southern Patagonia is commented and discussed in the light of current global change. articulo.oa?id=322062959008 New records are provided from both Región de Aysén and Región de Magallanes. -

Phytogeography and Zoogeography—Rafting Vs Continental Drift
JOURNAL OF CREATION 29(1) 2015 || PAPERS Phytogeography and zoogeography—rafting vs continental drift Dominic Statham Evolutionists have great difficulties explaining the global distributions of plants and animals. Accepted models of continental drift are inadequate to explain both trans-Atlantic and trans-Pacific disjunctions. At the same time, evolutionary biogeographers are unable to provide an adequate mechanism by which these distribution patterns could have arisen by dispersal. In contrast, the data fit well within a creationist model where plants and animals were rafted to the places they now inhabit on log mats left over from the Genesis Flood. The more raftable animals tend to have the most numerous transoceanic disjunctions and areas of high endemism/biodiversity tend to be concentrated in coastal regions where ocean currents intersect with land masses. Areas of high plant endemism/biodiversity often coincide with areas of high animal endemism/biodiversity, suggesting that the plants and animals were transported to these places by the same means. “ he pattern of geographical distribution [of plants haven’t changed significantly over such a long period of Tand animals] is just what you would expect if time. Furthermore, according to evolution theory, many evolution had happened.” (Richard Dawkins, Oxford plants and animals with transoceanic disjunct distributions University 1) originated millions of years after the continents are said to “Biogeography (or geographical distribution of have drifted apart.6–11 organisms) has not -

A Case of Gynandry in Oxyopes Salticus Hentz, 1845 (Oxyopidae)
NOTA BREVE: A case of gynandry in Oxyopes salticus Hentz, 1845 (Oxyopidae) Miguel Simó, Álvaro Laborda & Nadia Falero Abstract: The occurrence of a gynandromorph specimen of Oxyopes salticus, from grassland in the Departamento de Canelones, Uruguay, is reported. The exem- plar presents a bilateral gynandry, with the left part of the body male and the NOTA BREVE: right one female. This is the first case for this species. A case of gynandry in Oxyopes Key words: Araneae, Gynandromorph, Oxyopes salticus salticus Hentz, 1845 (Oxyopidae) Miguel Simó, Álvaro Laborda & Nadia Falero Un caso de ginandromorfo en Oxyopes salticus Hentz, 1845 Sección Entomología. Facultad de (Oxyopidae) Ciencias. Iguá 4225. CP 11400. Mon- tevideo. Uruguay. Resumen: [email protected] Se reporta el hallazgo de un ejemplar ginandromorfo de Oxyopes salticus. hallado en una pradera en el Departamento de Canelones , Uruguay. El indi- viduo presenta un ginandromorfismo bilateral, siendo la parte izquierda mas- culina y la derecha femenina. Se trata del primer caso indicado para esta es- Revista Ibérica de Aracnología pecie. ISSN: 1576 - 9518. Palabras clave: Araneae. Ginandromorfo. Oxyopes salticus. Dep. Legal: Z-2656-2000. Vol. 14, 31-XII-2006 Sección: Artículos y Notas. Pp: 179 − 181. Fecha publicación: 25 Octubre 2007 Introduction A specimen is considered gynandromorph when normally developed parts of Edita: the body are female and others parts are male. In spiders this phenomenon Grupo Ibérico de Aracnología (GIA) has been reported for the first time by Blackwall (1867). Different combina- Grupo de trabajo en Aracnología tions of morphological and physiological expressions of gynandry are possi- de la Sociedad Entomológica Aragone- ble.