A Comparison of Survey and National Accounts Based Local Area Models and Multipliers
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
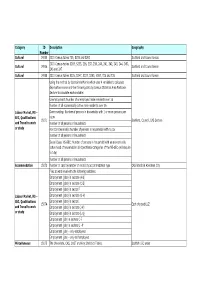
List of Tables
Category ID Description Geography Number Cultural 14925 2001 Census tables T25, S235 and S203 Scotland and Council areas 2001 Census tables S203, S235, 236, 237, 238, 240, 241, 242, 243, 244, 245, Cultural 14926 Scotland and Council areas 246 and 247 Cultural 14988 2001 Census tables S235, S247, S237, S203, KS07, T25 and T26 Scotland and Council areas Using the method by Carstairs & Morris which uses 4 variables to calculate deprivation scores and the following data by Census Statistics Area Postcode Sectors to calculate each variable: Unemployment: Number of unemployed male residents over 16 Number of all economically active male residents over 16 Labour Market, NS – Overcrowding: Number of persons in households with 1 or more persons per SEC, Qualifications room 15071 Scotland, Council, CAS Sectors and Travel to work Number of all persons in households or study Non Car Ownership: Number of persons in households with no car Number of all persons in households Social Class/ NS-SEC: Number of persons in household with an economically active head of household in all Operational Categories of the NE-SEC (will require to 1dp) Number of all persons in households Accommodation 15073 Number of cars by number of rooms by accommodation type CAS Wards in Aberdeen City Files at ward level with the following variables: Employment (jobs) in sectors (A-B) Employment (jobs) in sectors (C-E) Employment (jobs) in sector F Labour Market, NS – Employment (jobs) in sectors (G-H) SEC, Qualifications Employment (jobs) in sector I 15074 Each city and LUZ and Travel to work Employment (jobs) in sectors (J-K) or study Employment (jobs) in sectors (L-Q) Employment (job) in sectors C-F Employment (job) in sectors G –P Employment (job) – only employees Employment (job) – only self employed Miscellaneous 15075 The Univariate, CAS, CAST and Key Statistics Tables. -

The Right to Really Know Campaign
THE RIGHT TO REALLY KNOW CAMPAIGN REPORT ON PHASE 1 February 2001 The Right to Really Know Campaign 0 Friends of the Earth Scotland Executive Summary Increasing emphasis is being placed on the public's right of access to information and, in particular, information that relates to the environment. Recent public consultation on a Freedom of Information Bill in Scotland and a forthcoming European convention (the Aarhus Convention) have brought these issues to attention in Scotland. In order to inform the current debate and to provide information for the Scottish Executive, Friends of the Earth Scotland developed the Right to Really Know campaign. The campaign was designed to test the current system for the provision of environmental information. The Right to Really Know campaign has now been expanded into the Access All Areas campaign. The campaign has been completed and this report presents the findings. The Right to Really Know campaign resulted in 87 letters being written to the Scottish Environment Protection Agency, Local Authorities and Local Enterprise Companies across Scotland. The letters asked for simple environmental information or for policy statements on Sustainable development. The findings are as follows: of the 87 letters sent, seven never received a reply (8%); three of the replies received took longer than the 2 months currently allowed by the Environmental Information Regulations (1998) (3%); a total of ten responses (or lack of them) have therefore contravened existing guidelines on access to environmental information (11%); a further six responses failed to meet the future 1 month deadline that is proposed within the Aarhus convention (7%). -

Annual Report 1997-98
Annual Report 1997-98 Working with Scotland’s people to care for our natural heritage To the Right Honourable Donald Dewar MP Her Majesty’s Secretary of State for Scotland Sir, I have the honour to present the report of Scottish Natural Heritage, covering the period 1 April 1997 to 31 March 1998. I am, Sir, your most obedient servant, Magnus Magnusson KBE Scottish Natural Heritage Chairman 12 Hope Terrace Edinburgh EH9 2AS November 1998 Laid before Parliament under Section 10 of the Natural Heritage (Scotland) Act 1991 i Board Members at 31 March 1998 SNH BOARD Bill Howatson Chairman Robert Kay Magnus Magnusson KBE Jim McCarthy Deputy Chairman Professor John McManus Professor Christopher Smout CBE Captain Anthony Wilks Professor Seaton Baxter OBE Nan Burnett OBE WEST AREAS BOARD Simon Fraser* Chairman Barbara Kelly OBE Barbara Kelly CBE David Laird Vice Chairman Professor Fred Last Colin Carnie Ivor Lewis Lady Isobel Glasgow Peter Mackay CB Dr James Hansom Peter Peacock CBE Dr Ralph Kirkwood Bill Ritchie+ Robin Malcolm Professor Roger Wheater OBE Dr Malcolm Ogilvie Dr Phil Ratcliffe NORTH AREAS BOARD Richard Williamson Chairman Bill Ritchie+ SCIENTIFIC ADVISORY COMMITTEE Simon Fraser* Professor Paul Racey Vice Chairman Vice Chairman Amanda Bryan Professor John Davenport Dr Michael Foxley Ian Currie Nigel J O Graham Professor Charles Gimingham OBE Hugh Halcro-Johnston Dr Ralph Kirkwood Isobel Holbourn Dr James Hansom Dr Jim Hunter Professor Fred Last Annie MacDonald Professor T Jeff Maxwell Janet Price Professor Jack Matthews Michael Scott Professor John McManus Dr Kenneth Swanson Dr Malcolm Ogilvie Dr Philip Ratcliffe EAST AREAS BOARD Michael Scott Chairman Professor Brian Staines Nan Burnett OBE Professor Roger Wheater OBE Vice Chairman Andrew Bradford Ian Currie + until 31 December 1997 Elizabeth Hay * from 1 February 1998 Register of Board Members’ Interests SNH maintains a public register of Board members’ interests. -

GEM Scotland 2007 and 2008
Global Entrepreneurship Monitor Scotland 2007/8 Jonathan Levie Colin Mason Contents Page 3 Foreword Sir Tom Hunter 4 Chapter 1 Introduction 7 Chapter 2 Summary Highlights for GEM Scotland 2007 and 2008 8 Chapter 3 Entrepreneurial Business Attitudes, Activity and Aspirations in Scotland: 2007/08 Update 14 Chapter 4 Home-based businesses 20 Chapter 5 The Location of Entrepreneurial Activity in Scotland 25 Chapter 6 Entrepreneurship Training 30 Chapter 7 Scottish Entrepreneurship Policy and Programmes Review 2007 and 2008 31 Chapter 8 GEM and Entrepreneurship Policy in Scotland 32 Appendix 1 Data for this study were provided by the Global Entrepreneurship Research Association. Names of the members of national teams, the global coordination team, and the financial sponsors are published in the Global Entrepreneurship Monitor 2007 and 2008 Reports, which can be downloaded at www.gemconsortium.org. We thank all the researchers and their financial supporters who made this research possible. Whilst this work is based on data collected by the GEM consortium, responsibility for analysis and interpretation of those data is the sole responsibility of the authors. 1 List of Tables and Figures Foreword Table 3.1 (Page 8) not nascent or existing business owner- Figure 3.5 (Page 12) Entrepreneurial attitudes among non-entre- managers) Informal Investment rate in Scotland, UK preneurial individuals in the Scottish, UK and and Arc of Prosperity nations, 2002-2008 Arc of Prosperity adult population samples, Table 6.1 (Page 25) (% of respondents aged 18-64 who invested 2002 to 2008 (% agree with statement) Prevalence of business or enterprise training in someone else’s new business in the last GEM Scotland marks an important point in GEM Scotland delivers a critique of our by training provider and age group, combined three years) Table 3.2 (Page 10) 2006 and 2007 sample (ages 18-44 only) Scotland’s future as we face the results of an entrepreneurial culture, we need to keep pushing Scottish and benchmark TEA rates, 2007 Figure 5.1 (Page 20) unprecedented global economic meltdown. -

Business Support Published in Scotland by the Scottish Parliamentary Corporate Body
Published 20 February 2019 SP Paper 470 2nd Report 2019 (Session 5) Economy, Energy and Fair Work Committee Comataidh Eaconamaidh, Lùth is Obair Chothromach Business Support Published in Scotland by the Scottish Parliamentary Corporate Body. All documents are available on the Scottish For information on the Scottish Parliament contact Parliament website at: Public Information on: http://www.parliament.scot/abouttheparliament/ Telephone: 0131 348 5000 91279.aspx Textphone: 0800 092 7100 Email: [email protected] © Parliamentary copyright. Scottish Parliament Corporate Body The Scottish Parliament's copyright policy can be found on the website — www.parliament.scot Economy, Energy and Fair Work Committee Business Support, 2nd Report 2019 (Session 5) Contents Executive summary______________________________________________________1 Introduction ____________________________________________________________9 Context and background _________________________________________________9 Characteristics of business base ___________________________________________9 Inquiry engagement ___________________________________________________ 11 Complexity or clutter? The broader business support landscape _______________13 Background, roles and responsibilities of Business Gateway __________________16 Background __________________________________________________________16 Roles and responsibilities _______________________________________________18 Strategic alignment and accountability ____________________________________21 Original remit and policy drift -

The Dingwall Agenda
The Dingwall Agenda A Discussion Document for Land Reform and Rural Development in Scotland By Frank W. Rennie For Ross And Cromarty District Council Development Services Station Road Freepost Dingwall IV15 9BE There are no photocopying restrictions to the material contained in this publication but an acknowledgement of the source is requested 2 The Dingwall Agenda Introduction The text of this booklet is based upon a presentation made to a seminar on "Land Tenure in the Highlands and Islands - A new Approach", and the subsequent discussion which it engendered. This seminar was organised by Ross and Cromarty District Council and held in Dingwall in 1994. For this reason, the case for land reform in Scotland largely follows a Highlands and Islands perspective. This is not to be minimised, for the area covers more than 50% of the land surface of Scotland. Nor is it to be trivialised, for the legacy of injustice and mismanagement of the land resource of this country reaches its nadir in the history of the clearances and the land ownership patterns which to a very large extent have remained with us to this day. Those who deign to believe that these historical occurrences have little to do with the development of a modern society need only to look at the wave of emotional support which was generated by the Assynt Crofters Trust, or by the saga of Eigg, or any one of a dozen other confrontations between the resident rural population and our would-be benefactors. The support for land reform in Scotland grows almost every month. -

Caithness Profile Summary
The Caithness Conversation Community Profile May 2013 Funded by RWE npower renewables i Glossary ....................................................................................... iv Introduction .................................................................................. x SECTION 1 – OBSERVATIONS BY FOUNDATION SCOTLAND ............. 1 SECTION 2 – THE PROFILE............................................................... 6 1 Geography and Administration ................................................. 6 2 Strategic Context ...................................................................... 8 3 Voluntary and Community Activity ......................................... 16 4 Population ............................................................................. 21 5 Economy ................................................................................ 26 6 Employment & Income Levels ................................................. 32 7 Education and Training ........................................................... 39 8 Transport and Access to Services ............................................ 43 9 Housing and Health ................................................................ 46 10 Natural and Cultural Heritage ................................................. 49 11 Caithness Profile summary ..................................................... 52 SECTION 3 – THE CAITHNESS CONVERSATION .............................. 54 1 Who participated in the Caithness Conversation? ................... 54 2 What was the methodology? -

Fife Local Economic Forum Area
Fife Local Economic Forum Area Population Profile: Fife LEF at June 2001 The Figure below summarises population, employment, unemployment and job related training. Population Profile 350,400 161,000 8,677 38,000 Mid-year total population estimates People of working age in employment Claimant count unemployment Working age people receiving job related training Source: Mid- year total population estimates: General Register Office for Scotland, 2000 Other: Office for National Statistics, Spring 2001 The percentage of people in work based training is 10.8%. 120 Number of Organisations involved in Providing Community Based Learning (Matrixes completed by Fife Council (at June 2001) Type of Provision by Number of Providers 15 8 13 18 Core Skills Personal Development Adult Classes Youth work Source: Fife Council, June 2001 Fife Council: Projects Provision Type of Learning Client Group Project Name IT Core Pers Adult Youth Older Unem Ethnic Disbld Fam skills Dev. Class Class Learn Community Learning 3 3 3 3 3 3 3 3 3 Support Arts, Libraries and 3 3 3 3 3 3 Museums Sports and Leisure 3 3 3 3 3 3 3 Countryside Services 3 3 3 3 3 3 3 3 Vocational Training (Fife 3 3 3 3 3 3 Council) Fife Council Social Work 3 3 3 3 3 3 3 3 Services Scottish Enterprise Fife 3 3 3 3 3 3 3 W.E.A. 3 3 3 3 3 3 Youth First 3 3 3 3 3 3 Scout Association 3 3 3 3 Guide Association 3 3 3 3 Duke of Edinburgh 3 3 3 3 3 3 Award West Fife Enterprises 3 3 3 3 3 3 3 BRAG 3 3 3 3 3 3 3 Volunteering Fife 3 3 3 3 3 3 3 Health Promotion 3 3 3 3 3 3 3 3 Disability Sport Fife 3 3 3 3 3 3 3 YM/YWCA 3 3 3 3 3 3 3 3 3 There are 18 providers within the Fife Council area. -

Government Support for Small and Medium Business Enterprises in Scotland and Wales Since Devolution
GOVERNMENT SUPPORT FOR SMALL AND MEDIUM BUSINESS ENTERPRISES IN SCOTLAND AND WALES SINCE DEVOLUTION Professor John R.G. Jenkins, Fisher Graduate School of International Management, Monterey Institute of International Studies, Monterey, California, U.S.A. This paper summarizes the findings of a recent review of government efforts to support Small and Medium-Sized Enterprises (SMEs) in Scotland and Wales since the devolution, in 1999, of some administrative powers from the U.K. central government in London to new national governments in Edinburgh and Cardiff respectively. The writer formulated the following two hypotheses prior to this review, namely that 1. Increased funding, over and above annual increases in GVA (Gross Value Added, or the value of all the goods and services produced) has been made available, since Devolution, to Scottish and Welsh quasi-automous bodies designed to attract outside investment and assist SMEs. 2. At the same time, the new governments have required greater efficiency and accountablity from these business-development organizations in the latters’ efforts to provide support for all businesses, including SMEs. This paper will use the new European Commission definition of Micro, Small and Medium-sized businesses, which will come into effect on January 1, 2005, i.e. Micro Enterprises are defined as those having fewer than ten employees and annual sales (turnover) of less than two million Euros; Small Enterprises have 11-50 employees and sales of E2-10 million, while Medium-(Sized) Enterprises have 51-250 employees and sales of E11-50 million (EntreNews, 2003). At present Scotland and Wales use somewhat different – and generally stricter – criteria for their definitions of SMEs, but this will not affect the findings and conclusions of the report that follows. -

Staying on the Land: the Search for Cultural and Economic Sustainability in the Highlands and Islands of Scotland
University of Montana ScholarWorks at University of Montana Graduate Student Theses, Dissertations, & Professional Papers Graduate School 1996 Staying on the land: The search for cultural and economic sustainability in the Highlands and Islands of Scotland Mick Womersley The University of Montana Follow this and additional works at: https://scholarworks.umt.edu/etd Let us know how access to this document benefits ou.y Recommended Citation Womersley, Mick, "Staying on the land: The search for cultural and economic sustainability in the Highlands and Islands of Scotland" (1996). Graduate Student Theses, Dissertations, & Professional Papers. 5151. https://scholarworks.umt.edu/etd/5151 This Thesis is brought to you for free and open access by the Graduate School at ScholarWorks at University of Montana. It has been accepted for inclusion in Graduate Student Theses, Dissertations, & Professional Papers by an authorized administrator of ScholarWorks at University of Montana. For more information, please contact [email protected]. Maureen and Mike MANSFIELD LIBRARY The University o fMONTANA Permission is granted by the author to reproduce this material in its entirety, provided that this material is used for scholarly purposes and is properly cited in published works and reports. ** Please check "Yes" or "No" and provide signature ** Yes, I grant permission _ X No, I do not grant permission ____ Author's Signature D ate__________________ p L Any copying for commercial purposes or financial gain may be undertaken only with the author's explicit consent. STAYING ON THE LAND: THE SEARCH FOR CULTURAL AND ECONOMIC SUSTAINABILITY IN THE HIGHLANDS AND ISLANDS OF SCOTLAND by Mick Womersley B.A. -

Orkney and Shetland Area Waste Plan
Orkney and Shetland Area Waste Plan Prepared by SEPA March 2003 Orkney and Shetland Area Waste Plan 1 Contents Foreword by Orkney and Shetland Waste Strategy Group Chair 5 Foreword by Scottish Executive 6 Executive Summary 7 Key Acronyms 11 1 Introduction and Context 12 1.1 Background 12 1.2 Key Aims and Core Objectives 12 1.3 Developing an Integrated Plan 13 1.4 Area Description 14 1.5 Current Waste-Management Practice within Orkney and Shetland 14 1.5.1 Municipal Solid Waste Management 15 1.5.2 Non-Municipal Solid Waste Management 18 1.5.3 Existing Waste-Management Facilities 20 2 Strategic Framework and Drivers for Change 22 2.1 Introduction 22 2.2 Definition of Waste 22 2.3 Sustainable Waste Management 22 2.4 The EU Landfill Directive 22 2.4.1 Diversion of Biodegradable Municipal Solid Waste (BMW) 22 2.4.2 Landfill Permits 24 2.4.3 Other Technical Requirements 25 2.5 Landfill Tax 25 2.6 National Waste-Strategy Principles 25 2.6.1 The Waste Hierarchy 26 2.6.2 The Proximity Principle and Self-Sufficiency 27 2.6.3 The Best Practicable Environmental Option 27 3 Orkney and Shetland Best Practicable Environmental Option (BPEO) for Municipal Solid Waste (MSW) - The Strategy for Change 28 3.1 Introduction 28 3.2 The BPEO for MSW – detailed targets and actions 29 3.2.1 Waste Prevention 31 3.2.2 Recycling and Composting 33 3.2.3 Other Recovery 34 3.2.4 Disposal to Landfill 34 3.3 Household Hazardous Wastes 35 3.4 Performance Targets 35 3.5 Implementing the BPEO for MSW 38 3.6 Costs and Funding of the BPEO for MSW 38 3.7 Recycling Market Development -

Island Sustainable Energy Action Plan
ISLAND SUSTAINABLE ENERGY ACTION PLAN Outer Hebrides 25 July 2011 ISLAND SUSTAINABLE ENERGY ACTION PLAN Outer Hebrides EXECUTIVE SUMMARY i The Outer Hebrides comprise a chain of islands off the west coast of Scotland from Lewis in the north through Harris, North Uist, Benbecula and South Uist to Barra in the South. The entire population is 26,190 with 8,000 of that population centred around the main town of Stornoway in Lewis. The islands have an ageing population. By 2024, the number of people over 65 is projected to account for 31% of the entire population. The area is sparsely populated with a density of only 9 pelple per square kilometre compared to a Scottish average of 65. ii Crofting is the predominant land use with 80% of land held in crofting tenure and subject to unique crofting law. The islands have a unique Gaelic culture with the Gaelic language forming a major component of the history and culture of the Outer Hebrides. Almost 60% of inhabitants speak the language and the Outer Hebrides are recognised as the global centre of the language. iii The Outer Hebrides economy can be described as ‘fragile’ with an over dependence on the public sector and relentless decline in some of the traditional industries. The public sector accounts for 43% of total employment compared to a Scottish average of 23%. Annual Gross Domestic Regional Product is £382m or £14,500 per capita. Growth is evident in Harris Tweed, food production and the creative industries but the economic driver with the highest potential for growth is renewable energy.