Mutual Fund Liquidity Transformation and Reverse Flight to Liquidity*
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Repo Haircuts and Economic Capital: a Theory of Repo Pricing Wujiang Lou1 1St Draft February 2016; Updated June, 2020
Repo Haircuts and Economic Capital: A Theory of Repo Pricing Wujiang Lou1 1st draft February 2016; Updated June, 2020 Abstract A repurchase agreement lets investors borrow cash to buy securities. Financier only lends to securities’ market value after a haircut and charges interest. Repo pricing is characterized with its puzzling dual pricing measures: repo haircut and repo spread. This article develops a repo haircut model by designing haircuts to achieve high credit criteria, and identifies economic capital for repo’s default risk as the main driver of repo pricing. A simple repo spread formula is obtained that relates spread to haircuts negative linearly. An investor wishing to minimize all-in funding cost can settle at an optimal combination of haircut and repo rate. The model empirically reproduces repo haircut hikes concerning asset backed securities during the financial crisis. It explains tri-party and bilateral repo haircut differences, quantifies shortening tenor’s risk reduction effect, and sets a limit on excess liquidity intermediating dealers can extract between money market funds and hedge funds. Keywords: repo haircut model, repo pricing, repo spread, repo formula, repo pricing puzzle. JEL Classification: G23, G24, G33 A repurchase agreement (repo) is an everyday securities financing tool that lets investors borrow cash to fund the purchase or carry of securities by using the securities as collateral. In its typical transaction form, the borrower of cash or seller sells a security to the lender at an initial purchase price and agrees to purchase it back at a predetermined repurchase price on a future date. On the repo maturity date T, the lender (or the buyer) sells the security back to the borrower. -
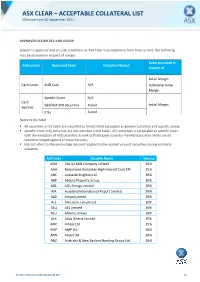
Asx Clear – Acceptable Collateral List 28
et6 ASX CLEAR – ACCEPTABLE COLLATERAL LIST Effective from 20 September 2021 APPROVED SECURITIES AND COVER Subject to approval and on such conditions as ASX Clear may determine from time to time, the following may be provided in respect of margin: Cover provided in Instrument Approved Cover Valuation Haircut respect of Initial Margin Cash Cover AUD Cash N/A Additional Initial Margin Specific Cover N/A Cash S&P/ASX 200 Securities Tiered Initial Margin Equities ETFs Tiered Notes to the table . All securities in the table are classified as Unrestricted (accepted as general Collateral and specific cover); . Specific cover only securities are not included in the table. Any securities is acceptable as specific cover, with the exception of ASX securities as well as Participant issued or Parent/associated entity issued securities lodged against a House Account; . Haircut refers to the percentage discount applied to the market value of securities during collateral valuation. ASX Code Security Name Haircut A2M The A2 Milk Company Limited 30% AAA Betashares Australian High Interest Cash ETF 15% ABC Adelaide Brighton Ltd 30% ABP Abacus Property Group 30% AGL AGL Energy Limited 20% AIA Auckland International Airport Limited 30% ALD Ampol Limited 30% ALL Aristocrat Leisure Ltd 30% ALQ ALS Limited 30% ALU Altium Limited 30% ALX Atlas Arteria Limited 30% AMC Amcor Ltd 15% AMP AMP Ltd 20% ANN Ansell Ltd 30% ANZ Australia & New Zealand Banking Group Ltd 20% © 2021 ASX Limited ABN 98 008 624 691 1/7 ASX Code Security Name Haircut APA APA Group 15% APE AP -

Complete Guide for Trading Pump and Dump Stocks
Complete Guide for Trading Pump and Dump Stocks Pump and dump stocks make me sick and just to be clear I do not trade these setups. When I look at a stock chart I normally see bulls and bears battling to see who will come out on top. However, when I look at a pump and dump stock it just saddens me. For those of you that watched the show Spartacus, it’s like when Gladiators have to fight outside of the arena and in dark alleys. As I see the sharp incline up and subsequent collapse, I think of all the poor souls that have lost IRA accounts, college savings and down payments for their homes. Well in this article, I’m going to cover 2 ways you can profit from these setups and clues a pump and dump scenario is taking place. Before we hit the two strategies, let’s first ground ourselves on the background of pump and dump stocks. What is a Pump and Dump Stock? These are stocks that shoot up like a rocket in a short period of time, only to crash down just as quickly shortly thereafter. The stocks often come out of nowhere and then the buzz on them reaches a feverish pitch. We can break the pump and dump down into three phases. Pump and Dump Phases Phase 1 – The Markup Every phase of the pump and dump scheme are challenging, but phase one is really tricky. The ring of thieves need to come up with an entire plan of attack to drum up excitement for the security but more importantly people pulling out their own cash. -

Markets Committee Central Bank Collateral Frameworks and Practices
Markets Committee Central bank collateral frameworks and practices A report by a Study Group established by the Markets Committee This Study Group was chaired by Guy Debelle, Assistant Governor of the Reserve Bank of Australia March 2013 This publication is available on the BIS website (www.bis.org). © Bank for International Settlements 2013. All rights reserved. Brief excerpts may be reproduced or translated provided the source is stated. ISBN 92-9131-926-0 (print) ISBN 92-9197-926-0 (online) Preface In July 2012, the Markets Committee established a Study Group to take stock of how collateral frameworks and practices compare across central banks and the key changes they have undergone since mid-2007. This initiative followed from the fact that, in the light of recent experience with market stress and other underlying changes in the financial landscape, many central banks have re-examined and adapted their collateral policies. It is also a natural extension of the Committee’s previous work on central bank monetary policy and operating frameworks. The Study Group was chaired by Guy Debelle, Assistant Governor of the Reserve Bank of Australia. The Group completed an interim report for review by the Markets Committee in November 2012. The finalised report was presented to central bank Governors of the Global Economy Meeting in early March 2013. The subject matter of this study is of core relevance to central banking. I believe the report could become a reference piece for those who are interested in central bank liquidity operations in different jurisdictions. Moreover, given the growing attention focused on collateral-related issues in the broader financial system, this report, which covers one specific area of collateral practices, could also serve as factual input to the wider debate. -

Signs of a Slowdown Cast a Shadow Over Markets
Benjamin H Cohen (+41 61) 280 8921 [email protected] I. Overview of developments: Signs of a slowdown cast a shadow over markets During the fourth quarter of 2000, investors’ expectations of a slowing global economy contributed to a downward shift in yield curves, a widening of credit spreads and further declines in already weak equity markets. Market attention focused on the United States, where macroeconomic data reinforced the view that a slowdown was likely in the first half of 2001. Profit warnings and credit downgrades also weighed heavily on the equity and debt markets and signalled problems of excessive leverage in the corporate sector. Even the normally stable commercial paper markets experienced unusually wide and volatile credit spreads. Market movements also revealed the extent to which the US outlook led to a re-evaluation of growth prospects in other regions. An appreciation of the euro suggested that investors viewed the European economy as likely to maintain momentum, although a downward shift in the euro swaps curve also indicated a potential exposure to the impact of a US slowdown. A depreciation of the yen and a decline in the Tokyo stock market reflected perceptions of a return to weaker growth in Japan. Divergent sovereign spreads corresponded to distinctions investors made in their judgments about the outlook for the emerging economies, with some countries seen as facing severe challenges and others as experiencing an uneven but persistent recovery from recent crises. Markets in general turned around in January 2001. A surprise 50 basis point reduction in the Federal Reserve’s target for the federal funds rate on 3 January, followed by a further 50 basis point cut on 31 January, buoyed both the equity and bond markets, at least temporarily. -

Changes to DTC Collateral Haircuts
Important Notice The Depository Trust Company B #: 14411-20 Date: December 14, 2020 To: All Participants Category: Settlement From: DTC Risk Management Attention: Settlement Manager/Managing Director/Cashier Subject: Changes to DTC Collateral Haircuts Beginning February 5, 2021, for Settlement Date February 8, 2021, DTC will implement the following changes to modify the collateral value for certain securities, which may affect the value of positions applied to the Collateral Monitor: 1. Securities held as Net Additions in Participant accounts that are issued by any of the issuer banks listed in Table 1 in Appendix A to this Important Notice will be given a 100% haircut and assigned no collateral value. This change is being made to align with provisions of the joint DTC and NSCC committed 364-day line-of-credit facility with a consortium of banks (“LOC Agreement”), as described in greater detail in Appendix A below. 2. United States Agencies and GSE securities that are not rated or that are rated below Aa2/AA will receive a 100% haircut (Appendix B includes the current list of eligible collateral). 3. Zero-coupon United States treasury securities with maturities up to two years will receive a haircut of 2% compared to the current haircut of 5%. This change will provide Participants with additional collateral value for these securities at DTC (Appendix C includes the current list of eligible collateral). 4. Securities with no active market prices will receive a 100% haircut. This will apply to new securities during the initial issuance stage and to active securities where DTC has not received a vendor price the prior day (Appendix C includes the current list of eligible collateral). -

Speculation in the United States Government Securities Market
Authorized for public release by the FOMC Secretariat on 2/25/2020 Se t m e 1, 958 p e b r 1 1 To Members of the Federal Open Market Committee and Presidents of Federal Reserve Banks not presently serving on the Federal Open Market Committee From R. G. Rouse, Manager, System Open Market Account Attached for your information is a copy of a confidential memorandum we have prepared at this Bank on speculation in the United States Government securities market. Authorized for public release by the FOMC Secretariat on 2/25/2020 C O N F I D E N T I AL -- (F.R.) SPECULATION IN THE UNITED STATES GOVERNMENT SECURITIES MARKET 1957 - 1958* MARKET DEVELOPMENTS Starting late in 1957 and carrying through the middle of August 1958, the United States Government securities market was subjected to a vast amount of speculative buying and liquidation. This speculation was damaging to mar- ket confidence,to the Treasury's debt management operations, and to the Federal Reserve System's open market operations. The experience warrants close scrutiny by all interested parties with a view to developing means of preventing recurrences. The following history of market events is presented in some detail to show fully the significance and continuous effects of the situation as it unfolded. With the decline in business activity and the emergence of easier Federal Reserve credit and monetary policy in October and November 1957, most market elements expected lower interest rates and higher prices for United States Government securities. There was a rapid market adjustment to these expectations. -

RG96-033 Addition of a New Class of Nasdaq-100 Index® Options Due To
Regulatory Circular RG96-33 Date: April 4, 1996 To: Members and Member Organizations From: Office of the Chairman Re: Addition of a New Class of Nasdaq-100 Index® Options Due to a Change in the Method of Calculating Exercise-Settlement Value Summary: The Chicago Mercantile Exchange (“CME”) anticipates receiving approval from the Commodity Futures Trading Commission to list Nasdaq-100 Index futures and futures options contracts and plans to commence trading in these instruments on Wednesday, April 10, 1996. Nasdaq-100 Index futures contracts at the CME have been designed with a different expiration- settlement value methodology than the calculation used to determine the settlement value currently employed in conjunction with Nasdaq-100 Index Options (ticker symbol NDX and overflow symbol NDZ) at the Chicago Board Options Exchange (“CBOE”). To facilitate hedging and arbitrage strategies by market participants in Nasdaq-100 Index derivatives, the CBOE has filed with the Securities and Exchange Commission an amendment to its rules to allow for a new class of Nasdaq-100 Index Options with an exercise-settlement value calculation methodology which conforms with the one to be employed by the CME. Approval of this rule change is anticipated prior to April 10, 1996. This circular explains the effects of the change on CBOE policies and procedures, and the manner in which existing and new Nasdaq-100 Index Options series will be identified for trading. Ticker Symbol Changes and Nasdaq-100 Index Options Class Addition: To implement this rule change it is necessary to create a new class of Nasdaq-100 Index Options which will be listed in parallel with the existing class. -

US Commercial Banks' Securities
ecommunications hqnittee on Energy and Commerce, House of Representatives - September 1988 INTERNATIONAL FINANCE a United States General Accounting Office Washington, D.C. 20548 Comptroller General of the United States B-229444 September 8, 1988 The Honorable Edward J. Markey Chairman, Subcommittee on Telecommunications and Finance Committee on Energy and Commerce House of Representatives Dear Mr. Chairman: At your request, we reviewed how U.S. commercial banks performed their securities underwriting and trading activities in the London mar- kets’ during 1986 and 1987 to assess how they might handle such activi- ties within the United States if the Glass-Steagall Act of 1933 were revised or repealed. The Glass-Steagall Act’s prohibition against the underwriting and trad- ing of corporate debt and equity securities by commercial banks applies to business conducted within the United States. According to the Federal Reserve’s Regulation K,’ banks may underwrite and trade securities outside the United States, within certain limits. These activities may be undertaken by subsidiaries of the bank holding company or by subsidi- aries of the bank itself, but not by branches, which are permitted to underwrite only local government securities. U.S. commercial banks conduct the greatest concentration of their over- seas underwriting and trading activities in London. Approximately 50 U.S. commercial banks operate in London, and 18 of them engage in at least a minimal amount of underwriting and trading. The range and type of such activities varies among these 18 banks. Most are large banks; 16 are considered money-center or super-regional banks. Bank examination reports from the Federal Reserve, the New York State Banking Department, and the Office of the Comptroller of the Currency indicate that most of the London securities subsidiaries of U.S. -

Crashes and Collateralized Lending Working Paper
Crashes and Collateralized Lending Jakub W. Jurek Erik Stafford Working Paper 11-025 Copyright © 2010 by Jakub W. Jurek and Erik Stafford Working papers are in draft form. This working paper is distributed for purposes of comment and discussion only. It may not be reproduced without permission of the copyright holder. Copies of working papers are available from the author. Crashes and Collateralized Lending Jakub W. Jurek and Erik Stafford∗ Abstract This paper develops a parsimonious static model for characterizing financing terms in collateralized lending markets. We characterize the systematic risk exposures for a variety of securities and develop a simple indifference-pricing framework to value the systematic crash risk exposure of the collateral. We then apply Modigliani and Miller's (1958) Proposition Two (MM) to split the cost of bearing this risk between the borrower and lender, resulting in a schedule of haircuts and financing rates. The model produces comparative statics and time-series dynamics that are consistent with the empirical features of repo market data, including the credit crisis of 2007-2008. First draft: April 2010 This draft: July 2010 ∗Jurek: Bendheim Center for Finance, Princeton University; [email protected]. Stafford: Harvard Business School; estaff[email protected]. We thank Joshua Coval and seminar participants at the University of Oregon for helpful comments and discussions. An important service provided by financial intermediaries in the support of capital market trans- actions is the financing of security purchases by investors. Investors can buy securities with margin, whereby they contribute a portion of the purchase price and borrow the remainder from the intermedi- ary in the form of a collateralized, non-recourse short-term loan. -

Interpretations of FINRA's Margin Rule
3/21 (RN No. 21-13) 174 4210. Margin Requirements (Continued) (f) Other Provisions (Continued) (8) Special Initial and Maintenance Margin Requirements (Continued) member at which a customer seeks to open an account or to resume day trading knows or has a reasonable basis to believe that the customer will engage in pattern day trading, then the special requirements under paragraph (f)(8)(B)(iv) of this Rule will apply. /01 Multiple Purchases and Sales If a customer enters an order to purchase a security and sells the same security within the same day, but for reasons beyond the customer’s control e.g., price, the purchase was executed in smaller blocks, it will be considered as one day trade. However, the member must be able to demonstrate that it was the customer’s intent to execute one day trade. This will also apply to when a customer enters a sale order and buys the same security within the same day. In addition, the trades would have to have been executed in sequential order. One purchase and several subsequent sale transactions of the same security, where the sales were executed in sequential order within the same day, shall constitute one day trade. One sale and several subsequent purchases of the same security, where the purchases were executed in sequential order within the same day, shall also constitute one day trade. /02 Multiple Purchases and Sales – Alternative Method Rather than counting day trades based on the number of transactions a customer executes to establish or increase a position that is liquidated on the same day (as set out in Interpretation /01 above) a firm may instead count day trades based on the number of times during the day that the day trading customer changes its trading direction (i.e., changes from buying a particular security to selling it, or FKDQJHVIURPVHOOLQJDSDUWLFXODUVHFXULW\WREX\LQJLW ௗ Example A: 09:30 Buy 250 ABC 09:31 Buy 250 ABC 13:00 Sell 500 ABC The customer has executed one day trade. -

The Benchmark US Treasury Market: Recent Performance
Michael J. Fleming The Benchmark U.S. Treasury Market: Recent Performance and Possible Alternatives he U.S. Treasury securities market is a benchmark. As crisis in the fall of 1998 in a so-called “flight to quality.” A Tobligations of the U.S. government, Treasury securities are related “flight to liquidity” also caused yield spreads among considered to be free of default risk. The market is therefore a Treasury securities of varying liquidity to widen sharply. benchmark for risk-free interest rates, which are used to Consequently, some of the attributes that make the Treasury forecast economic developments and to analyze securities in market an attractive benchmark were adversely affected. other markets that contain default risk. The Treasury market is This paper examines the benchmark role of the U.S. also large and liquid, with active repurchase agreement (repo) Treasury market and the features that make it an attractive and futures markets. These features make it a popular benchmark. In it, I examine the market’s recent performance, benchmark for pricing other fixed-income securities and for including yield changes relative to other fixed-income markets, hedging positions taken in other markets. changes in liquidity, repo market developments, and the The Treasury market’s benchmark status, however, is now aforementioned flight to liquidity. I show that several of the being called into question by the nation’s improved fiscal attributes that make the U.S. Treasury market a useful situation. The U.S. government has run a budget surplus over benchmark were negatively affected by the events of fall 1998, the past two years, and surpluses are expected to continue (and and that some of these attributes did not quickly return to their to continue growing) for years.