DOCSLIB.ORG

Optimization Methods in Finance

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Optimization Methods in Finance Optimization Methods in Finance Gerard Cornuejols Reha Tut¨ unc¨ u¨ Carnegie Mellon University, Pittsburgh, PA 15213 USA January 2006 2 Foreword Optimization models play an increasingly important role in financial de- cisions. Many computational finance problems ranging from asset allocation to risk management, from option pricing to model calibration can be solved efficiently using modern optimization techniques. This course discusses sev- eral classes of optimization problems (including linear, quadratic, integer, dynamic, stochastic, conic, and robust programming) encountered in finan- cial models. For each problem class, after introducing the relevant theory (optimality conditions, duality, etc.) and efficient solution methods, we dis- cuss several problems of mathematical finance that can be modeled within this problem class. In addition to classical and well-known models such as Markowitz' mean-variance optimization model we present some newer optimization models for a variety of financial problems. Acknowledgements This book has its origins in courses taught at Carnegie Mellon University in the Masters program in Computational Finance and in the MBA program at the Tepper School of Business (G´erard Cornu´ejols), and at the Tokyo In- stitute of Technology, Japan, and the University of Coimbra, Portugal (Reha Tut¨ unc¨ u).¨ We thank the attendants of these courses for their feedback and for many stimulating discussions. We would also like to thank the colleagues who provided the initial impetus for this project, especially Michael Trick, John Hooker, Sanjay Srivastava, Rick Green, Yanjun Li, Lu´ıs Vicente and Masakazu Kojima. Various drafts of this book were experimented with in class by Javier Pena,~ Fran¸cois Margot, Miroslav Karamanov and Kathie Cameron, and we thank them for their comments. Contents 1 Introduction 9 1.1 Optimization Problems . 9 1.1.1 Linear Programming . 10 1.1.2 Quadratic Programming . 11 1.1.3 Conic Optimization . 11 1.1.4 Integer Programming . 12 1.1.5 Dynamic Programming . 13 1.2 Optimization with Data Uncertainty . 13 1.2.1 Stochastic Programming . 13 1.2.2 Robust Optimization . 14 1.3 Financial Mathematics . 15 1.3.1 Portfolio Selection and Asset Allocation . 16 1.3.2 Pricing and Hedging of Options . 18 1.3.3 Risk Management . 19 1.3.4 Asset/Liability Management . 20 2 Linear Programming: Theory and Algorithms 21 2.1 The Linear Programming Problem . 21 2.2 Duality . 23 2.3 Optimality Conditions . 26 2.4 The Simplex Method . 29 2.4.1 Basic Solutions . 30 2.4.2 Simplex Iterations . 33 2.4.3 The Tableau Form of the Simplex Method . 37 2.4.4 Graphical Interpretation . 40 2.4.5 The Dual Simplex Method . 41 2.4.6 Alternatives to the Simplex Method . 43 3 LP Models: Asset/Liability Cash Flow Matching 45 3.1 Short Term Financing . 45 3.1.1 Modeling . 46 3.1.2 Solving the Model with SOLVER . 48 3.1.3 Interpreting the output of SOLVER . 51 3.1.4 Modeling Languages . 52 3.1.5 Features of Linear Programs . 53 3.2 Dedication . 54 3.3 Sensitivity Analysis for Linear Programming . 56 3 4 CONTENTS 3.3.1 Short Term Financing . 56 3.3.2 Dedication . 61 3.4 Case Study . 64 4 LP Models: Asset Pricing and Arbitrage 67 4.1 The Fundamental Theorem of Asset Pricing . 67 4.1.1 Replication . 69 4.1.2 Risk-Neutral Probabilities . 70 4.1.3 The Fundamental Theorem of Asset Pricing . 72 4.2 Arbitrage Detection Using Linear Programming . 73 4.3 Additional Exercises . 76 4.4 Case Study: Tax Clientele Effects in Bond Portfolio Manage- ment . 80 5 Nonlinear Programming: Theory and Algorithms 83 5.1 Introduction . 83 5.2 Software . 85 5.3 Univariate Optimization . 86 5.3.1 Binary search . 86 5.3.2 Newton's Method . 90 5.3.3 Approximate Line Search . 93 5.4 Unconstrained Optimization . 95 5.4.1 Steepest Descent . 95 5.4.2 Newton's Method . 99 5.5 Constrained Optimization . 102 5.5.1 The generalized reduced gradient method . 105 5.5.2 Sequential Quadratic Programming . 110 5.6 Nonsmooth Optimization: Subgradient Methods . 111 6 NLP Models: Volatility Estimation 113 6.1 Volatility Estimation with GARCH Models . 113 6.2 Estimating a Volatility Surface . 117 7 Quadratic Programming: Theory and Algorithms 123 7.1 The Quadratic Programming Problem . 123 7.2 Optimality Conditions . 124 7.3 Interior-Point Methods . 126 7.4 The Central Path . 129 7.5 Interior-Point Methods . 130 7.5.1 Path-Following Algorithms . 130 7.5.2 Centered Newton directions . 131 7.5.3 Neighborhoods of the Central Path . 133 7.5.4 A Long-Step Path-Following Algorithm . 136 7.5.5 Starting from an Infeasible Point . 136 7.6 QP software . 137 7.7 Additional Exercises . 137 CONTENTS 5 8 QP Models: Portfolio Optimization 139 8.1 Mean-Variance Optimization . 139 8.1.1 Example . 141 8.1.2 Large-Scale Portfolio Optimization . 146 8.1.3 The Black-Litterman Model . 149 8.1.4 Mean-Absolute Deviation to Estimate Risk . 153 8.2 Maximizing the Sharpe Ratio . 155 8.3 Returns-Based Style Analysis . 158 8.4 Recovering Risk-Neural Probabilities from Options Prices . 160 8.5 Additional Exercises . 164 8.6 Case Study . 166 9 Conic Optimization Tools 169 9.1 Introduction . 169 9.2 Second-order cone programming: . 169 9.2.1 Ellipsoidal Uncertainty for Linear Constraints . 171 9.2.2 Conversion of quadratic constraints into second-order cone constraints . 173 9.3 Semidefinite programming: . 174 9.3.1 Ellipsoidal Uncertainty for Quadratic Constraints . 176 9.4 Algorithms and Software . 177 10 Conic Optimization Models in Finance 179 10.1 Tracking Error and Volatility Constraints . 179 10.2 Approximating Covariance Matrices . 182 10.3 Recovering Risk-Neural Probabilities from Options Prices . 185 10.4 Arbitrage Bounds for Forward Start Options . 187 10.4.1 A Semi-Static Hedge . 188 11 Integer Programming: Theory and Algorithms 193 11.1 Introduction . 193 11.2 Modeling Logical Conditions . 194 11.3 Solving Mixed Integer Linear Programs . 197 11.3.1 Linear Programming Relaxation . 197 11.3.2 Branch and Bound . 198 11.3.3 Cutting Planes . 206 11.3.4 Branch and Cut . 210 12 IP Models: Constructing an Index Fund 213 12.1 Combinatorial Auctions . 213 12.2 The Lockbox Problem . 214 12.3 Constructing an Index Fund . 217 12.3.1 A Large-Scale Deterministic Model . 218 12.3.2 A Linear Programming Model . 221 12.4 Portfolio Optimization with Minimum Transaction Levels . 222 12.5 Exercises . 223 12.6 Case Study . 224 6 CONTENTS 13 Dynamic Programming Methods 225 13.1 Introduction . 225 13.1.1 Backward Recursion . 228 13.1.2 Forward Recursion . 231 13.2 Abstraction of the Dynamic Programming Approach . 232 13.3 The Knapsack Problem. 235 13.3.1 Dynamic Programming Formulation . 235 13.3.2 An Alternative Formulation . 236 13.4 Stochastic Dynamic Programming . 237 14 DP Models: Option Pricing 239 14.1 A Model for American Options . 239 14.2 Binomial Lattice . 241 14.2.1 Specifying the parameters . 242 14.2.2 Option Pricing . 243 15 DP Models: Structuring Asset Backed Securities 247 15.1 Data . 249 15.2 Enumerating possible tranches . 251 15.3 A Dynamic Programming Approach . 252 15.4 Case Study . 253 16 Stochastic Programming: Theory and Algorithms 255 16.1 Introduction . 255 16.2 Two Stage Problems with Recourse . 256 16.3 Multi Stage Problems . 258 16.4 Decomposition . 260 16.5 Scenario Generation . 263 16.5.1 Autoregressive model . 263 16.5.2 Constructing scenario trees . 265 17 SP Models: Value-at-Risk 271 17.1 Risk Measures . 271 17.2 Minimizing CVaR . 274 17.3 Example: Bond Portfolio Optimization . 276 18 SP Models: Asset/Liability Management 279 18.1 Asset/Liability Management . 279 18.1.1 Corporate Debt Management . 282 18.2 Synthetic Options . 285 18.3 Case Study: Option Pricing with Transaction Costs . 288 18.3.1 The Standard Problem . 289 18.3.2 Transaction Costs . 290 19 Robust Optimization: Theory and Tools 293 19.1 Introduction to Robust Optimization . 293 19.2 Uncertainty Sets . ..
Load more

Recommended publications
  • Researchers in Computational Finance / Quant Portfolio Analysts Limassol, Cyprus
    Researchers in Computational Finance / Quant Portfolio Analysts Limassol, Cyprus Award winning Hedge Fund is seeking to build their team with top researchers to join their offices in Limassol, Cyprus. IKOS is an investment advisor that deploys quantitative hedge fund strategies to trade the global financial markets, with a long and successful track record. This is an exciting opportunity to join a fast growing company that is focused on the development of the best research and trading infrastructure. THE ROLE We are looking for top class mathematicians to work with us in modern quantitative finance. Our researchers participate in novel financial analysis and development efforts that require significant application of mathematical modelling techniques. The position involves working within the Global Research team; there is also significant interaction with the trading and fund management teams. The objective is the development of innovative products and computational methods in the equities, futures, currency and fixed income markets. In addition, the role involves statistical analysis of portfolio risk and returns, involvement in the portfolio management process and monitoring and analysing transactions on an ongoing basis. THE INDIVIDUAL The successful candidates will have a first class degree and practical science or engineering problem solving skills through a PhD in mathematics or mathematical sciences, together with excellent all round analytical and programming abilities. The following skills are also prerequisites for the job:
    [Show full text]
  • A Lagrangian Decomposition Approach Combined with Metaheuristics for the Knapsack Constrained Maximum Spanning Tree Problem
    MASTERARBEIT A Lagrangian Decomposition Approach Combined with Metaheuristics for the Knapsack Constrained Maximum Spanning Tree Problem ausgeführt am Institut für Computergraphik und Algorithmen der Technischen Universität Wien unter der Anleitung von Univ.-Prof. Dipl.-Ing. Dr.techn. Günther Raidl und Univ.-Ass. Dipl.-Ing. Dr.techn. Jakob Puchinger durch Sandro Pirkwieser, Bakk.techn. Matrikelnummer 0116200 Simmeringer Hauptstraße 50/30, A-1110 Wien Datum Unterschrift Abstract This master’s thesis deals with solving the Knapsack Constrained Maximum Spanning Tree (KCMST) problem, which is a so far less addressed NP-hard combinatorial optimization problem belonging to the area of network design. Thereby sought is a spanning tree whose profit is maximal, but at the same time its total weight must not exceed a specified value. For this purpose a Lagrangian decomposition approach, which is a special variant of La- grangian relaxation, is applied to derive upper bounds. In the course of the application the problem is split up in two subproblems, which are likewise to be maximized but easier to solve on its own. The subgradient optimization method as well as the Volume Algorithm are deployed to solve the Lagrangian dual problem. To derive according lower bounds, i.e. feasible solutions, a simple Lagrangian heuristic is applied which is strengthened by a problem specific local search. Furthermore an Evolutionary Algorithm is presented which uses a suitable encoding for the solutions and appropriate operators, whereas the latter are able to utilize heuristics based on defined edge-profits. It is shown that simple edge-profits, derived straightforward from the data given by an instance, are of no benefit.
    [Show full text]
  • Chapter 8 Stochastic Gradient / Subgradient Methods
    Chapter 8 Stochastic gradient / subgradient methods Contents (class version) 8.0 Introduction........................................ 8.2 8.1 The subgradient method................................. 8.5 Subgradients and subdifferentials................................. 8.5 Properties of subdifferentials.................................... 8.7 Convergence of the subgradient method.............................. 8.10 8.2 Example: Hinge loss with 1-norm regularizer for binary classifier design...... 8.17 8.3 Incremental (sub)gradient method............................ 8.19 Incremental (sub)gradient method................................. 8.21 8.4 Stochastic gradient (SG) method............................. 8.23 SG update.............................................. 8.23 Stochastic gradient algorithm: convergence analysis....................... 8.26 Variance reduction: overview................................... 8.33 Momentum............................................. 8.35 Adaptive step-sizes......................................... 8.37 8.5 Example: X-ray CT reconstruction........................... 8.41 8.1 © J. Fessler, April 12, 2020, 17:55 (class version) 8.2 8.6 Summary.......................................... 8.50 8.0 Introduction This chapter describes two families of algorithms: • subgradient methods • stochastic gradient methods aka stochastic gradient descent methods Often we turn to these methods as a “last resort,” for applications where none of the methods discussed previously are suitable. Many machine learning applications,
    [Show full text]
  • Master of Science in Finance (MSF) 1
    Master of Science in Finance (MSF) 1 MASTER OF SCIENCE IN FINANCE (MSF) MSF 501 MSF 505 Mathematics with Financial Applications Futures, Options, and OTC Derivatives This course provides a systematic exposition of the primary This course provides the foundation for understanding the price mathematical methods used in financial economics. Mathematical and risk management of derivative securities. The course starts concepts and methods include logarithmic and exponential with simple derivatives, e.g., forwards and futures, and develops functions, algebra, mean-variance analysis, summations, matrix the concept of arbitrage-free pricing and hedging. Based upon algebra, differential and integral calculus, and optimization. The the work of Black, Scholes, and Merton, the course extends their course will include a variety of financial applications including pricing model through the use of lattices, Monte Carlo simulation compound interest, present and future value, term structure of methods, and more advanced strategies. Mathematical tools in interest rates, asset pricing, expected return, risk and measures stochastic processes are gradually introduced throughout the of risk aversion, capital asset pricing model (CAPM), portfolio course. Particular emphasis is given to the pricing of interest rate optimization, expected utility, and consumption capital asset pricing derivatives, e.g., FRAs, swaps, bond options, caps, collars, and (CCAPM). floors. Lecture: 3 Lab: 0 Credits: 3 Prerequisite(s): MSF 501 with min. grade of C and MSF 503 with min. grade of C and MSF 502 with min. grade of C MSF 502 Lecture: 3 Lab: 0 Credits: 3 Statistical Analysis in Financial Markets This course presents and applies statistical and econometric MSF 506 techniques useful for the analysis of financial markets.
    [Show full text]
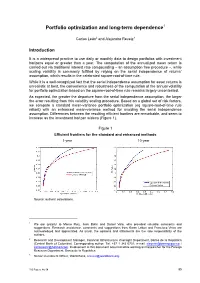
  • Portfolio Optimization and Long-Term Dependence1
    Portfolio optimization and long-term dependence1 Carlos León2 and Alejandro Reveiz3 Introduction It is a widespread practice to use daily or monthly data to design portfolios with investment horizons equal or greater than a year. The computation of the annualized mean return is carried out via traditional interest rate compounding – an assumption free procedure –, while scaling volatility is commonly fulfilled by relying on the serial independence of returns’ assumption, which results in the celebrated square-root-of-time rule. While it is a well-recognized fact that the serial independence assumption for asset returns is unrealistic at best, the convenience and robustness of the computation of the annual volatility for portfolio optimization based on the square-root-of-time rule remains largely uncontested. As expected, the greater the departure from the serial independence assumption, the larger the error resulting from this volatility scaling procedure. Based on a global set of risk factors, we compare a standard mean-variance portfolio optimization (eg square-root-of-time rule reliant) with an enhanced mean-variance method for avoiding the serial independence assumption. Differences between the resulting efficient frontiers are remarkable, and seem to increase as the investment horizon widens (Figure 1). Figure 1 Efficient frontiers for the standard and enhanced methods 1-year 10-year Source: authors’ calculations. 1 We are grateful to Marco Ruíz, Jack Bohn and Daniel Vela, who provided valuable comments and suggestions. Research assistance, comments and suggestions from Karen Leiton and Francisco Vivas are acknowledged and appreciated. As usual, the opinions and statements are the sole responsibility of the authors.
    [Show full text]
  • MIE 1612: Stochastic Programming and Robust Optimization
    MIE 1612: Stochastic Programming and Robust Optimization Fall 2019 Syllabus Instructor: Prof. Merve Bodur Office: BA8106 Office hour: Wednesday 2-3pm (or by appointment) E-mail: [email protected] P.S. Please include course code (MIE 1612) in your email subject TA: Maryam Daryalal Office hour: Monday 2:30-3:30pm, in BA8119 (or by appointment) E-mail: [email protected] P.S. Please include course code (MIE 1612) in your email subject Lectures: Monday 4-6pm (GB119) and Wednesday 1-2pm (GB303) Suggested texts: Lectures on Stochastic Programming { Modeling and Theory, SIAM, Shapiro, Dentcheva, and Ruszczy´nski,2009. Introduction to Stochastic Programming, Springer-Verlag, Birge and Louveaux, 2011. Stochastic Programming, Wiley, Kall and Wallace, 1994. Stochastic Programming, Handbooks in OR and MS, Elsevier, Ruszczy´nskiand Shapiro, 2003. Robust Optimization, Princeton University Press, Ben-Tal, El Ghaoui, and Nemirovski, 2009. Course web pages: Quercus, Piazza Official course description: Stochastic programming and robust optimization are optimization tools deal- ing with a class of models and algorithms in which data is affected by uncertainty, i.e., some of the input data are not perfectly known at the time the decisions are made. Topics include modeling uncertainty in optimization problems, two-stage and multistage stochastic programs with recourse, chance constrained pro- grams, computational solution methods, approximation and sampling methods, and applications. Knowledge of linear programming, probability and statistics are required, while programming ability and knowledge of integer programming are helpful. Prerequisite: MIE262, APS1005 or equivalent, and MIE231, APS106S or equivalent. 1 Overview The aim of stochastic programming and robust optimization is to find optimal decisions in problems which involve uncertain data.
    [Show full text]
  • From Arbitrage to Arbitrage-Free Implied Volatilities
    Journal of Computational Finance 20(3), 31–49 DOI: 10.21314/JCF.2016.316 Research Paper From arbitrage to arbitrage-free implied volatilities Lech A. Grzelak1,2 and Cornelis W. Oosterlee1,3 1Delft Institute of Applied Mathematics, Delft University of Technology, Mekelweg 4, 2628 CD, Delft, The Netherlands; email: [email protected] 2ING, Quantiative Analytics, Bijlmerplein 79, 1102 BH, Amsterdam, The Netherlands 3CWI: National Research Institute for Mathematics and Computer Science, Science Park 123, 1098 XG, Amsterdam, The Netherlands; email: [email protected] (Received October 14, 2015; revised March 6, 2016; accepted March 7, 2016) ABSTRACT We propose a method for determining an arbitrage-free density implied by the Hagan formula. (We use the wording “Hagan formula” as an abbreviation of the Hagan– Kumar–Le´sniewski–Woodward model.) Our method is based on the stochastic collo- cation method. The principle is to determine a few collocation points on the implied survival distribution function and project them onto the polynomial of an arbitrage- free variable for which we choose the Gaussian variable. In this way, we have equality in probability at the collocation points while the generated density is arbitrage free. Analytic European option prices are available, and the implied volatilities stay very close to those initially obtained by the Hagan formula. The proposed method is very fast and straightforward to implement, as it only involves one-dimensional Lagrange interpolation and the inversion of a linear system of equations. The method is generic and may be applied to other variants or other models that generate arbitrage. Keywords: arbitrage-free density; collocation method; orthogonal projection; arbitrage-free volatility; SCMC sampler; implied volatility parameterization.
    [Show full text]
  • Careers in Quantitative Finance by Steven E
    Careers in Quantitative Finance by Steven E. Shreve1 August 2018 1 What is Quantitative Finance? Quantitative finance as a discipline emerged in the 1980s. It is also called financial engineering, financial mathematics, mathematical finance, or, as we call it at Carnegie Mellon, computational finance. It uses the tools of mathematics, statistics, and computer science to solve problems in finance. Computational methods have become an indispensable part of the finance in- dustry. Originally, mathematical modeling played the dominant role in com- putational finance. Although this continues to be important, in recent years data science and machine learning have become more prominent. Persons working in the finance industry using mathematics, statistics and computer science have come to be known as quants. Initially relegated to peripheral roles in finance firms, quants have now taken center stage. No longer do traders make decisions based solely on instinct. Top traders rely on sophisticated mathematical models, together with analysis of the current economic and financial landscape, to guide their actions. Instead of sitting in front of monitors \following the market" and making split-second decisions, traders write algorithms that make these split- second decisions for them. Banks are eager to hire \quantitative traders" who know or are prepared to learn this craft. While trading may be the highest profile activity within financial firms, it is not the only critical function of these firms, nor is it the only place where quants can find intellectually stimulating and rewarding careers. I present below an overview of the finance industry, emphasizing areas in which quantitative skills play a role.
    [Show full text]
  • Financial Mathematics
    Financial Mathematics Alec Kercheval (Chair, Florida State University) Ronnie Sircar (Princeton University) Jim Sochacki (James Madison University) Tim Sullivan (Economics, Towson University) Introduction Financial Mathematics developed in the mid-1980s as research mathematicians became interested in problems, largely involving stochastic control, that had until then been studied primarily by economists. The subject grew slowly at first and then more rapidly from the mid- 1990s through to today as mathematicians with backgrounds first in probability and control, then partial differential equations and numerical analysis, got into it and discovered new issues and challenges. A society of mostly mathematicians and some economists, the Bachelier Finance Society, began in 1997 and holds biannual world congresses. The Society for Industrial and Applied Mathematics (SIAM) started an Activity Group in Financial Mathematics & Engineering in 2002; it now has about 800 members. The 4th SIAM conference in this area was held jointly with its annual meeting in Minneapolis in 2013, and attracted over 300 participants to the Financial Mathematics meeting. In 2009 the SIAM Journal on Financial Mathematics was launched and it has been very successful gauged by numbers of submissions. Student interest grew enormously over the same period, fueled partly by the growing financial services sector of modern economies. This growth created a demand first for quantitatively trained PhDs (typically physicists); it then fostered the creation of a large number of Master’s programs around the world, especially in Europe and in the U.S. At a number of institutions undergraduate programs have developed and become quite popular, either as majors or tracks within a mathematics major, or as joint degrees with Business or Economics.
    [Show full text]
  • Financial Engineering and Computational Finance with R Rmetrics Built 221.10065
    Rmetrics An Environment for Teaching Financial Engineering and Computational Finance with R Rmetrics Built 221.10065 Diethelm Würtz Institute for Theoretical Physics Swiss Federal Institute of Technology, ETH Zürich Rmetrics is a collection of several hundreds of functions designed and written for teaching "Financial Engineering" and "Computational Finance". Rmetrics was initiated in 1999 as an outcome of my lectures held on topics in econophysics at ETH Zürich. The family of the Rmetrics packages build on ttop of the statistical software environment R includes members dealing with the following subjects: fBasics - Markets and Basic Statistics, fCalendar - Date, Time and Calendar Management, fSeries - The Dynamical Process Behind Financial Markets, fMultivar - Multivariate Data Analysis, fExtremes - Beyond the Sample, Dealing with Extreme Values, fOptions – The Valuation of Options, and fPortfolio - Portfolio Selection and Optimization. Rmetrics has become the premier open source to download data sets from the Internet. The solution for financial market analysis and valu- major concern is given to financial return series ation of financial instruments. With hundreds of and their stylized facts. Distribution functions functions build on modern and powerful methods relevant in finance are added like the stable, the Rmetrics combines explorative data analysis and hyperbolic, or the normal inverse Gaussian statistical modeling with object oriented rapid distribution function to compute densities, pro- prototyping. Rmetrics is embedded in R, both babilities, quantiles and random deviates. Esti- building an environment which creates especially mators to fit the distributional parameters are for students and researchers in the third world a also available. Furthermore, hypothesis tests for first class system for applications in statistics and the investigation of distributional properties, of finance.
    [Show full text]
  • Subgradient Method
    Subgradient Method Ryan Tibshirani Convex Optimization 10-725/36-725 Last last time: gradient descent Consider the problem min f(x) x n for f convex and differentiable, dom(f) = R . Gradient descent: (0) n choose initial x 2 R , repeat (k) (k−1) (k−1) x = x − tk · rf(x ); k = 1; 2; 3;::: Step sizes tk chosen to be fixed and small, or by backtracking line search If rf Lipschitz, gradient descent has convergence rate O(1/) Downsides: • Requires f differentiable this lecture • Can be slow to converge next lecture 2 Subgradient method n Now consider f convex, with dom(f) = R , but not necessarily differentiable Subgradient method: like gradient descent, but replacing gradients with subgradients. I.e., initialize x(0), repeat (k) (k−1) (k−1) x = x − tk · g ; k = 1; 2; 3;::: where g(k−1) 2 @f(x(k−1)), any subgradient of f at x(k−1) Subgradient method is not necessarily a descent method, so we (k) (0) (k) keep track of best iterate xbest among x ; : : : x so far, i.e., f(x(k) ) = min f(x(i)) best i=0;:::k 3 Outline Today: • How to choose step sizes • Convergence analysis • Intersection of sets • Stochastic subgradient method 4 Step size choices • Fixed step sizes: tk = t all k = 1; 2; 3;::: • Diminishing step sizes: choose to meet conditions 1 1 X 2 X tk < 1; tk = 1; k=1 k=1 i.e., square summable but not summable Important that step sizes go to zero, but not too fast Other options too, but important difference to gradient descent: all step sizes options are pre-specified, not adaptively computed 5 Convergence analysis n Assume that f convex, dom(f) = R , and also that f is Lipschitz continuous with constant G > 0, i.e., jf(x) − f(y)j ≤ Gkx − yk2 for all x; y Theorem: For a fixed step size t, subgradient method satisfies lim f(x(k) ) ≤ f ? + G2t=2 k!1 best Theorem: For diminishing step sizes, subgradient method sat- isfies lim f(x(k) ) = f ? k!1 best 6 Basic bound, and convergence rate (0) ? Letting R = kx − x k2, after k steps, we have the basic bound R2 + G2 Pk t2 f(x(k) ) − f(x?) ≤ i=1 i best Pk 2 i=1 ti Previous theorems follow from this.
    [Show full text]
  • An Efficient Solution Methodology for Mixed-Integer Programming Problems Arising in Power Systems" (2016)
    University of Connecticut OpenCommons@UConn Doctoral Dissertations University of Connecticut Graduate School 12-15-2016 An Efficient Solution Methodology for Mixed- Integer Programming Problems Arising in Power Systems Mikhail Bragin University of Connecticut - Storrs, [email protected] Follow this and additional works at: https://opencommons.uconn.edu/dissertations Recommended Citation Bragin, Mikhail, "An Efficient Solution Methodology for Mixed-Integer Programming Problems Arising in Power Systems" (2016). Doctoral Dissertations. 1318. https://opencommons.uconn.edu/dissertations/1318 An Efficient Solution Methodology for Mixed-Integer Programming Problems Arising in Power Systems Mikhail Bragin, PhD University of Connecticut, 2016 For many important mixed-integer programming (MIP) problems, the goal is to obtain near- optimal solutions with quantifiable quality in a computationally efficient manner (within, e.g., 5, 10 or 20 minutes). A traditional method to solve such problems has been Lagrangian relaxation, but the method suffers from zigzagging of multipliers and slow convergence. When solving mixed-integer linear programming (MILP) problems, the recently adopted branch-and-cut may also suffer from slow convergence because when the convex hull of the problems has complicated facial structures, facet- defining cuts are typically difficult to obtain, and the method relies mostly on time-consuming branching operations. In this thesis, the novel Surrogate Lagrangian Relaxation method is developed and its convergence is proved to the optimal multipliers, without the knowledge of the optimal dual value and without fully optimizing the relaxed problem. Moreover, for practical implementations a stepsizing formula, that guarantees convergence without requiring the optimal dual value, has been constructively developed. The key idea is to select stepsizes in a way that distances between Lagrange multipliers at consecutive iterations decrease, and as a result, Lagrange multipliers converge to a unique limit.
    [Show full text]