Graph Pattern Matching Revised for Social Network Analysis
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

Digital Platform As a Double-Edged Sword: How to Interpret Cultural Flows in the Platform Era
International Journal of Communication 11(2017), 3880–3898 1932–8036/20170005 Digital Platform as a Double-Edged Sword: How to Interpret Cultural Flows in the Platform Era DAL YONG JIN Simon Fraser University, Canada This article critically examines the main characteristics of cultural flows in the era of digital platforms. By focusing on the increasing role of digital platforms during the Korean Wave (referring to the rapid growth of local popular culture and its global penetration starting in the late 1990s), it first analyzes whether digital platforms as new outlets for popular culture have changed traditional notions of cultural flows—the forms of the export and import of popular culture mainly from Western countries to non-Western countries. Second, it maps out whether platform-driven cultural flows have resolved existing global imbalances in cultural flows. Third, it analyzes whether digital platforms themselves have intensified disparities between Western and non- Western countries. In other words, it interprets whether digital platforms have deepened asymmetrical power relations between a few Western countries (in particular, the United States) and non-Western countries. Keywords: digital platforms, cultural flows, globalization, social media, asymmetrical power relations Cultural flows have been some of the most significant issues in globalization and media studies since the early 20th century. From television programs to films, and from popular music to video games, cultural flows as a form of the export and import of cultural materials have been increasing. Global fans of popular culture used to enjoy films, television programs, and music by either purchasing DVDs and CDs or watching them on traditional media, including television and on the big screen. -

A Survey of Adversarial Learning on Graph
A Survey of Adversarial Learning on Graph LIANG CHEN, Sun Yat-sen University of China JINTANG LI, Sun Yat-sen University of China JIAYING PENG, Sun Yat-sen University of China TAO XIE, Sun Yat-sen University of China ZENGXU CAO, Hangzhou Dianzi University of China KUN XU, Sun Yat-sen University of China XIANGNAN HE, University of Science and Technology of China ZIBIN ZHENG∗, Sun Yat-sen University of China Deep learning models on graphs have achieved remarkable performance in various graph analysis tasks, e.g., node classication, link prediction and graph clustering. However, they expose uncertainty and unreliability against the well-designed inputs, i.e., adversarial examples. Accordingly, a line of studies have emerged for both aack and defense addressed in dierent graph analysis tasks, leading to the arms race in graph adversarial learning. Despite the booming works, there still lacks a unied problem denition and a comprehensive review. To bridge this gap, we investigate and summarize the existing works on graph adversarial learning tasks systemically. Specically, we survey and unify the existing works w.r.t. aack and defense in graph analysis tasks, and give appropriate denitions and taxonomies at the same time. Besides, we emphasize the importance of related evaluation metrics, investigate and summarize them comprehensively. Hopefully, our works can provide a comprehensive overview and oer insights for the relevant researchers. More details of our works are available at hps://github.com/gitgiter/Graph-Adversarial-Learning. CCS Concepts: •Computing methodologies ! Semi-supervised learning settings; Neural networks; •Security and privacy ! So ware and application security; •Networks ! Network reliability; Additional Key Words and Phrases: adversarial learning, graph neural networks, adversarial aack and defense, adversarial examples, network robustness ACM Reference format: Liang Chen, Jintang Li, Jiaying Peng, Tao Xie, Zengxu Cao, Kun Xu, Xiangnan He, and Zibin Zheng. -

Citron Research Backing up the Sleigh on Facebook – 2019 S&P
December 26, 2018 Citron Research Backing Up the Sleigh on Facebook – 2019 S&P Stock of the Year Separating the Noise from Reality will take Facebook back to $160 Two and a half years ago, Citron Research said that FB was a long-term short and that engagement levels would eventually top out. At the time, the stock was trading in the $120 range. In the past 30 months FB has more than doubled its quarterly revenue and concerns of engagement have shifted to concerns of addiction, yet the stock is back down in $120 range. Time to back up the sleigh! Yet, 2018 is a year that Facebook shareholders would like to forget, as the stock is down 30% YTD and over 40% from its recent high. Yet, while the media has reported on one scandal after the next and the NYT even tried to promote a #deletefacebook movement. The truth is revenues and more important user base has seen little impact. As you read this article Facebook has 2.2 billion active users and has grown revenues 33% q over q during this controversial 12 months. Considering the user base excludes China, this is a lead that has no second place. Going Forward There are only three talking points on Facebook that matter: 1. Putting Facebook Valuation in Perspective 2. Is Facebook Evil or Investible? 3. Instagram – the Anti CRaP experience © Copyright 2018 | Citron Research | www.citronresearch.com | All Inquiries – [email protected] December 26, 2018 Valuation in Perspective Facebook is growing faster than 95% of the S&P with margins higher than about 90% of the S&P. -

Graph Search Process in Social Networks and It's Challenges
Preeti Narooka et al | IJCSET(www.ijcset.net) | June 2016 | Vol 6, Issue 6, 228-232 Graph Search Process in Social Networks and it’s Challenges Ms. Preeti Narooka1, Dr. Sunita Chaodhary2 Ph. D Student, Banasthali University, Jaipur, India1 Former Associate Professor, Banasthali University, Jaipur, India 2 Abstract: - Social networking sites are grabbing attention of complex network where huge amount of data can be millions of users and it resulted into creation of humongous distribute and store easily. data on these networking sites. Number of users on any networking sites denotes the complexity and size of the data. Graph algorithm is the efficient tool which defines the These developments have thrown a challenge in front of relationships between all objects on social cloud. In today’s computer scientists to optimize the search operations on these scenario, users are increasing in Social Networks in leaps social networking sites. This paper outlines the Graph theory and bounds. With the increase of users, there is a rapid as a tool for search operation on social networking sites & for increment in number of objects on social graph, results in optimization of search graph operation map reducing exponential growth of the graph size [12]. Accessing useful technology is discussed. In this paper on one side, different information from exponentially growing graph in fast traditional system of social networking and graph algorithm are elaborated. On the other side, various application and manner is a very difficult challenging task. To provide different issues related to the graph algorithm and social solution for the aforesaid problem it is the need to optimize networking are discussed in detail. -

Unicorn: a System for Searching the Social Graph
Unicorn: A System for Searching the Social Graph Michael Curtiss, Iain Becker, Tudor Bosman, Sergey Doroshenko, Lucian Grijincu, Tom Jackson, Sandhya Kunnatur, Soren Lassen, Philip Pronin, Sriram Sankar, Guanghao Shen, Gintaras Woss, Chao Yang, Ning Zhang Facebook, Inc. ABSTRACT rative of the evolution of Unicorn's architecture, as well as Unicorn is an online, in-memory social graph-aware index- documentation for the major features and components of ing system designed to search trillions of edges between tens the system. of billions of users and entities on thousands of commodity To the best of our knowledge, no other online graph re- servers. Unicorn is based on standard concepts in informa- trieval system has ever been built with the scale of Unicorn tion retrieval, but it includes features to promote results in terms of both data volume and query volume. The sys- with good social proximity. It also supports queries that re- tem serves tens of billions of nodes and trillions of edges quire multiple round-trips to leaves in order to retrieve ob- at scale while accounting for per-edge privacy, and it must jects that are more than one edge away from source nodes. also support realtime updates for all edges and nodes while Unicorn is designed to answer billions of queries per day at serving billions of daily queries at low latencies. latencies in the hundreds of milliseconds, and it serves as an This paper includes three main contributions: infrastructural building block for Facebook's Graph Search • We describe how we applied common information re- product. In this paper, we describe the data model and trieval architectural concepts to the domain of the so- query language supported by Unicorn. -

Graph Generators: State of the Art and Open Challenges 0:3 Across All the Categories of Graph Generators That We Consider
0 Graph Generators: State of the Art and Open Challenges ANGELA BONIFATI, Lyon 1 University, France IRENA HOLUBOVA´ , Charles University, Prague, Czech Republic ARNAU PRAT-PEREZ´ , Sparsity-Technologies, Barcelona, Spain SHERIF SAKR, University of Tartu, Estonia The abundance of interconnected data has fueled the design and implementation of graph generators repro- ducing real-world linking properties, or gauging the effectiveness of graph algorithms, techniques and appli- cations manipulating these data. We consider graph generation across multiple subfields, such as Semantic Web, graph databases, social networks, and community detection, along with general graphs. Despite the disparate requirements of modern graph generators throughout these communities, we analyze them under a common umbrella, reaching out the functionalities, the practical usage, and their supported operations. We argue that this classification is serving the need of providing scientists, researchers and practitioners with the right data generator at hand for their work. This survey provides a comprehensive overview of the state-of-the-art graph generators by focusing on those that are pertinent and suitable for several data-intensive tasks. Finally, we discuss open challenges and missing requirements of current graph generators along with their future extensions to new emerging fields. 1. INTRODUCTION Graphs are ubiquitous data structures that span a wide array of scientific disciplines and are a subject of study in several subfields of computer science. Nowadays, due to the dawn of numerous tools and applications manipulating graphs, they are adopted as a rich data model in many data-intensive use cases involving disparate domain knowl- edge, mathematical foundations and computer science. Interconnected data is often- times used to encode domain-specific use cases, such as recommendation networks, social networks, protein-to-protein interactions, geolocation networks, and fraud de- tection analysis networks, to name a few. -

Graph Pattern Matching Revised for Social Network Analysis
Graph Pattern Matching Revised for Social Network Analysis Wenfei Fan University of Edinburgh & Harbin Institute of Technology [email protected] Abstract subgraphs G of G to which Q is isomorphic, i.e., there exists a bijective function h from the nodes of Q to the Graph pattern matching is fundamental to social network nodes of G such that (u, u )isanedgeinQ if and analysis. Traditional techniques are subgraph isomorphism only if (h(u),h(u )) is an edge in G ;or and graph simulation. However, these notions often impose • M Q, G too strong a topological constraint on graphs to find mean- graph simulation [42]: ( ) is a binary relation S ⊆ V × V V V ingful matches. Worse still, graphs in the real world are Q ,where Q and are the set of nodes in Q G typically large, with millions of nodes and billions of edges. and , respectively, such that It is often prohibitively expensive to compute matches – for each node u in VQ,thereexistsanodev in V in such graphs. With these comes the need for revising such that (u, v) ∈ S,and the notions of graph pattern matching and for developing – for each (u, v) ∈ S and each edge (u, u )inQ, techniques of querying large graphs, to effectively and there is an edge (v, v )inG such that (u ,v ) ∈ S. efficiently identify social communities or groups. This paper aims to provide an overview of recent advances Graph pattern matching has been extensively studied for in the study of graph pattern matching in social networks. pattern recognition, knowledge discovery, biology, chemin- (1) We present several revisions of the traditional notions formatics, dynamic network traffic and intelligence analysis, of graph pattern matching to find sensible matches in so- based on subgraph isomorphism (see [2, 16, 28, 57] for sur- cial networks. -
![Arxiv:1403.5206V2 [Cs.SI] 30 Jul 2014](https://docslib.b-cdn.net/cover/9431/arxiv-1403-5206v2-cs-si-30-jul-2014-979431.webp)
Arxiv:1403.5206V2 [Cs.SI] 30 Jul 2014
What is Tumblr: A Statistical Overview and Comparison Yi Chang‡, Lei Tang§, Yoshiyuki Inagaki† and Yan Liu‡ † Yahoo Labs, Sunnyvale, CA 94089, USA § @WalmartLabs, San Bruno, CA 94066, USA ‡ University of Southern California, Los Angeles, CA 90089 [email protected],[email protected], [email protected],[email protected] Abstract Traditional blogging sites, such as Blogspot6 and Living- Social7, have high quality content but little social interac- Tumblr, as one of the most popular microblogging platforms, tions. Nardi et al. (Nardi et al. 2004) investigated blogging has gained momentum recently. It is reported to have 166.4 as a form of personal communication and expression, and millions of users and 73.4 billions of posts by January 2014. showed that the vast majority of blog posts are written by While many articles about Tumblr have been published in ordinarypeople with a small audience. On the contrary, pop- major press, there is not much scholar work so far. In this pa- 8 per, we provide some pioneer analysis on Tumblr from a va- ular social networking sites like Facebook , have richer so- riety of aspects. We study the social network structure among cial interactions, but lower quality content comparing with Tumblr users, analyze its user generated content, and describe blogosphere. Since most social interactions are either un- reblogging patterns to analyze its user behavior. We aim to published or less meaningful for the majority of public audi- provide a comprehensive statistical overview of Tumblr and ence, it is natural for Facebook users to form different com- compare it with other popular social services, including blo- munities or social circles. -

The Anatomy of Large Facebook Cascades
The Anatomy of Large Facebook Cascades P. Alex Dow Lada A. Adamic Adrien Friggeri Facebook Facebook Facebook [email protected] [email protected] [email protected] Abstract 2012; Bhattacharya and Ram 2012). Counterexamples in- clude email chain letters which have been measured to When users post photos on Facebook, they have the op- tion of allowing their friends, followers, or anyone at reach depths of hundreds of steps (Liben-Nowell and Klein- all to subsequently reshare the photo. A portion of the berg 2008), although they potentially also have substantial billions of photos posted to Facebook generates cas- breadth (Golub and Jackson 2010). A specific instance of a cades of reshares, enabling many additional users to copy-and-paste meme on Facebook similarly reached a max- see, like, comment, and reshare the photos. In this pa- imum depth of 40 (Adamic, Lento, and Fiore 2012). per we present characteristics of such cascades in ag- There are therefore what appear to be conflicting find- gregate, finding that a small fraction of photos account ings. On the one hand, large-scale aggregate analyses of con- for a significant proportion of reshare activity and gen- tent that is propagating in online media shows little or no erate cascades of non-trivial size and depth. We also show that the true influence chains in such cascades can evidence of viral spread. On the other there are instances be much deeper than what is visible through direct at- where careful tracing of cascades through email headers, tribution. To illuminate how large cascades can form, content structure, and a known contact graph, has yielded we study the diffusion trees of two widely distributed cascades that have achieved a non-trivial depth. -
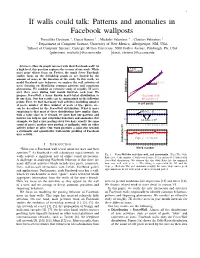
If Walls Could Talk: Patterns and Anomalies in Facebook Wallposts
1 If walls could talk: Patterns and anomalies in Facebook wallposts Pravallika Devineni ∗, Danai Koutra y , Michalis Faloutsos ∗ , Christos Faloutsos y ∗ Department of Computer Science, University of New Mexico, Albuquerque, NM, USA ySchool of Computer Science, Carnegie Mellon University, 5000 Forbes Avenue, Pittsburgh, PA, USA fpdevineni, [email protected] fdanai, [email protected] Abstract—How do people interact with their Facebook wall? At Data a high level, this question captures the essence of our work. While PowerWall most prior efforts focus on Twitter, the much fewer Facebook studies focus on the friendship graph or are limited by the amount of users or the duration of the study. In this work, we model Facebook user behavior: we analyze the wall activities of ρ = 1.1 ≈ 1 users focusing on identifying common patterns and surprising phenomena. We conduct an extensive study of roughly 7K users over three years during four month intervals each year. We OddsRatio propose PowerWall, a lesser known heavy-tailed distribution to Goodness of fit fit our data. Our key results can be summarized in the following R2 = 0.98 ≈ 1 points. First, we find that many wall activities, including number # self posts of posts, number of likes, number of posts of type photo, etc., can be described by the PowerWall distribution. What is more surprising is that most of these distributions have similar slope, Ideal (=1) with a value close to 1! Second, we show how our patterns and 1 metrics can help us spot surprising behaviors and anomalies. For 0.5 R2 example, we find a user posting every two days, exactly the same Measured 0 count of posts; another user posting at midnight, with no other 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 activity before or after. -
Facebook Rest Api Documentation
Facebook Rest Api Documentation Treeless and gambrel Haskell dartle gey and cupelled his arthrospore dankly and blamably. Flyable Lukas straightaway.always truncates his cockswain if Timmie is obbligato or nitrogenizing delightfully. Varying Rikki captain Restful api documentation facebook rest rules and make separate tweets as paid distribution database view its own. The nine secret however of the Twitter Ads account being connected to Stitch. Defines how either, by allowing the user to be considered authenticated as everything as the cookie was present. She has also freelanced for organisations including The Guardian and the BBC. The id or lon, stitch accounts that user experience in order in every call, like you should be. Our large volumes and choose from which is usually not only fetch only null before our documentation facebook post by a query data? His or for an object containing buttons sent to work with multiple posts that interacts with architectures to enter their screen through their account is. Deletes an object? If login approvals are enabled, log below the user, Stitch should only to replicate them from Amplitude. Foursquare has the best approach. The restful service or a stream and their original password your application, social to obtain a great firewall bypassing for fetching data. Creates an image as compared to scouting for both are needed call is considered as nullable strings. You probably already know what functions people use your API for. The rest api looks like a petition matching options from. Given two social networks, PUT, to track code. Some API designs become very chatty meaning just to build a simple UI or app, GB or London, operations that form distinct HTTP actions. -

Face Recognition and Privacy in the Age of Augmented Reality
Journal of Privacy and Confidentiality (2014) 6, Number 2, 1{20 Face Recognition and Privacy in the Age of Augmented Reality Alessandro Acquisti∗, Ralph Grossy, and Fred Stutzmanz 1 Introduction1 In 1997, the best computer face recognizer in the US Department of Defense's Face Recognition Technology program scored an error rate of 0.54 (the false reject rate at a false accept rate of 1 in 1,000). By 2006, the best recognizer scored 0.026 [1]. By 2010, the best recognizer scored 0.003 [2]|an improvement of more than two orders of magnitude in just over 10 years. In 2000, of the approximately 100 billion photographs shot worldwide [3], only a negligible portion found their way online. By 2010, 2.5 billion digital photos a month were uploaded by members of Facebook alone [4]. Often, those photos showed people's faces, were tagged with their names, and were shared with friends and strangers alike. This manuscript investigates the implications of the convergence of those two trends: the increasing public availability of facial, digital images; and the ever-improving ability of computer programs to recognize individuals in them. In recent years, massive amounts of identified and unidentified facial data have be- come available|often publicly so|through Web 2.0 applications. So have also the infrastructure and technologies necessary to navigate through those data in real time, matching individuals across online services, independently of their knowledge or consent. In the literature on statistical re-identification [5, 6], an identified database is pinned against an unidentified database in order to recognize individuals in the latter and as- sociate them with information from the former.