Pitch Sequence Complexity and Long-Term Pitcher Performance
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

BUYBACK AUTOGRAPHS A.J. Puk Aaron Nola Adam Ottavino Andrew
BUYBACK AUTOGRAPHS A.J. Puk Aaron Nola Adam Ottavino Andrew Benintendi Anthony Rizzo Austin Meadows Austin Riley Blake Snell Bo Bichette Bobby Bradley Brendan McKay Brendan Rodgers Bryce Harper Buster Posey Carter Kieboom Cesar Hernandez Charlie Morton Chris Sale Christian Vazquez Christian Yelich Clayton Kershaw Corey Dickerson Corey Kluber Daniel Vogelbach Dansby Swanson David Peralta David Price Dawel Lugo DJ LeMahieu Dominic Smith Dylan Cease Eloy Jimenez Eugenio Suarez Fernando Tatis Jr. Francisco Lindor Gavin Lux George Springer Gerrit Cole Gleyber Torres Hunter Dozier Hunter Pence Jack Flaherty Jake Bauers JD Martinez Jean Segura Joey Votto Jorge Alfaro Jorge Polanco Jose Altuve Josh Hader Josh Naylor Juan Soto Justin Smoak Keston Hiura Ketel Marte Kevin Newman Kohl Stewart Kris Bryant Kyle Hendicks Lance McCullers Jr. Lourdes Gurriel Jr. Lucas Giolito Luis Severino Matt Carpenter Matt Olson Max Kepler Max Muncy Max Scherzer Michael Chavis Miguel Cabrera Mike Clevinger Mike Trout Mitch Garver Mitch Haniger Mitch Keller Nick Senzel Nolan Arenado Ozzie Albies Patrick Corbin Paul DeJong Paul Goldschmidt Pete Alonso Renato Nunez Rhys Hoskins Ronald Acuña Jr. Rowdy Tellez Scott Kingery Shane Bieber Shin-Soo Choo Shohei Ohtani Tim Anderson Tommy La Stella Travis Shaw Trevor Bauer Trevor May Victor Robles Vladimir Guerrero Jr. Whit Merrifield Will Smith Willson Contreras Yasmani Grandal Zack Wheeler DUAL BUYBACK AUTOGRAPHS George Springer/Jose Altuve Houston Astros® Ronald Acuña Jr./Ozzie Albies Atlanta Braves™ Gleyber Torres/Miguel Andujar New York Yankees® Mike Trout/Shohei Ohtani Angels® Anthony Rizzo/Kris Bryant Chicago Cubs® Scott Kingery/Rhys Hoskins Philadelphia Phillies®. -

Cincinnati Reds'
Cincinnati Reds Press Clippings February 23, 2017 THIS DAY IN REDS HISTORY 1995 - Kevin Mitchell signs a contract to play for the Daiei Hawks in Japan. Mitchell spent three seasons with the Reds, batting .332 with 50 doubles, 55 home runs and 167 RBI MLB.COM 'Breaking' news: Cingrani develops cutter Reds lefty works in offseason to add another pitch offering By Mark Sheldon / MLB.com | @m_sheldon | February 22nd, 2017 + 50 COMMENTS GOODYEAR, Ariz. -- Reds left-hander Tony Cingrani can throw his four-seam fastball 95 mph, and consistent with his career, he used it often in 2016. It was so often that PITCHf/x data showed he threw his fastball more than 87 percent of the time. Cingrani started using a split-fingered fastball sometime in the second half, but he realized it was time to diversify the repertoire even more. He needed a breaking ball and used the offseason to develop a cut fastball. "It's just another way to get guys out," Cingrani said. "It gets hitters off thinking it's just going to be a fastball. I'm still trying to work on how I want that ball to move, but it's good and feels comfortable." At the suggestion of teammate and fellow reliever Caleb Cotham, Cingrani traveled to Kent, Wash., in the fall and worked out at Driveline Baseball. The facility, owned by Kyle Boddy, has gained a reputation for providing data-driven pitch training and also encourages building arm strength by playing catch with weighted balls. "Caleb is a pretty smart cat," Cingrani said. -

2020 MLB Ump Media Guide
the 2020 Umpire media gUide Major League Baseball and its 30 Clubs remember longtime umpires Chuck Meriwether (left) and Eric Cooper (right), who both passed away last October. During his 23-year career, Meriwether umpired over 2,500 regular season games in addition to 49 Postseason games, including eight World Series contests, and two All-Star Games. Cooper worked over 2,800 regular season games during his 24-year career and was on the feld for 70 Postseason games, including seven Fall Classic games, and one Midsummer Classic. The 2020 Major League Baseball Umpire Guide was published by the MLB Communications Department. EditEd by: Michael Teevan and Donald Muller, MLB Communications. Editorial assistance provided by: Paul Koehler. Special thanks to the MLB Umpiring Department; the National Baseball Hall of Fame and Museum; and the late David Vincent of Retrosheet.org. Photo Credits: Getty Images Sport, MLB Photos via Getty Images Sport, and the National Baseball Hall of Fame and Museum. Copyright © 2020, the offiCe of the Commissioner of BaseBall 1 taBle of Contents MLB Executive Biographies ...................................................................................................... 3 Pronunciation Guide for Major League Umpires .................................................................. 8 MLB Umpire Observers ..........................................................................................................12 Umps Care Charities .................................................................................................................14 -

2017 KANSAS CITY ROYALS Spring Training Game Notes Kansas City Royals (1-1) Vs
2017 KANSAS CITY ROYALS Spring Training Game Notes Kansas City Royals (1-1) vs. Seattle Mariners (2-0) Monday, February 27, 2017 ACE 30 HOME STREAK SNAPPED BY RANGERS--The Royals had their 8-game home winning streak that obviously dated back to last spring halted yesterday with a 6-4 loss to the Texas Rangers...KC’s the last two losses in Surprise Stadium have come at the hands of the Rangers, but yesterday’s was the first “home” loss in Surprise since March 13 of last year vs. Cleveland (KC also lost a “road” game to Texas to closeout last spring)...Texas plated a pair of first inning runs off of starting and losing hurler Kyle Zimmer, then tacked on another his his second inning of work...Kansas City got on the board in the third when Hunter Dozier tripled home pinch runner Peter O’Brien, but then the Royals were held in check until plating three in the ninth with the game ending with the tying run at the plate...20-year old non-roster catcher Chase Vallot made his presence felt offensively, collecting a double, triple and two RBI after spelling Mike Moustakas as the designated hitter...Scott Alexander, Bobby Parnell, Malcolm Culver and Peter Moylan each contributed a scoreless inning of relief from the hill. A WORLD BASEBALL SPRING--The Royals and the rest of Major League Baseball Upcoming Probables opened training camp early this year due to this being a WBC season...players from 16 Today @ Seattle Mariners @ Peoria Stadium (12:10) different countries will compete starting on March 6 in Seoul, Korea...other first round Jason Vargas (L), Joakim Soria, Mike Minor (L), Jonathan stops include Tokyo, Japan, Jalisco, Mexico and Miami, Florida...team USA, who will Sanchez (L), Andrew Edwards, Eric Stout (L), Al Alburquerque have Royals’ Eric Hosmer and Danny Duffy has been assigned the Miami pool, which vs. -

2019 Topps Series 1 Checklist
BASE VETERANS 1 Ronald Acuña Jr. Atlanta Braves™ Rookie Cup 2 Tyler Anderson Colorado Rockies™ 3 Eduardo Nunez Boston Red Sox® World Series Highlights 4 Dereck Rodriguez San Francisco Giants® Future Stars 5 Chase Anderson Milwaukee Brewers™ 6 Max Scherzer Washington Nationals® League Leaders 7 Gleyber Torres New York Yankees® Rookie Cup 8 Adam Jones Baltimore Orioles® 9 Ben Zobrist Chicago Cubs® 10 Clayton Kershaw Los Angeles Dodgers® 11 Mike Zunino Seattle Mariners™ 12 Crackin' Jokes Major League Baseball® 13 David Price Boston Red Sox® 14 The Yankees® Win! New York Yankees® 15 J.P. Crawford Philadelphia Phillies® 16 Charlie Blackmon Colorado Rockies™ 17 Caleb Joseph Baltimore Orioles® 18 Blake Parker Angels® 19 Jacob deGrom New York Mets® League Leaders 20 Jose Urena Miami Marlins® 21 Jean Segura Seattle Mariners™ 22 Adalberto Mondesi Kansas City Royals® 23 J.D. Martinez Boston Red Sox® League Leaders 24 Blake Snell Tampa Bay Rays™ League Leaders 25 Chad Green New York Yankees® 26 Angel Stadium™ Angels® 27 Mike Leake Seattle Mariners™ 28 Boston's Boys Boston Red Sox® 29 Eugenio Suarez Cincinnati Reds® 30 Josh Hader Milwaukee Brewers™ 31 Busch Stadium™ St. Louis Cardinals® 32 Carlos Correa Houston Astros® 33 Jacob Nix San Diego Padres™ Rookie 34 Josh Donaldson Cleveland Indians® 35 Joey Rickard Baltimore Orioles® 36 Paul Blackburn Oakland Athletics™ 37 Marcus Stroman Toronto Blue Jays® 38 Kolby Allard Atlanta Braves™ Rookie 39 Richard Urena Toronto Blue Jays® 40 Jon Lester Chicago Cubs® 41 Corey Seager Los Angeles Dodgers® 42 Edwin Encarnacion Cleveland Indians® 43 Nick Burdi Pittsburgh Pirates® Rookie 44 Jay Bruce New York Mets® 45 Nick Pivetta Philadelphia Phillies® 46 Jose Abreu Chicago White Sox® 47 Yankee Stadium™ New York Yankees® 48 PNC Park™ Pittsburgh Pirates® 49 Michael Kopech Chicago White Sox® Rookie 50 Mookie Betts Boston Red Sox® 51 Michael Brantley Cleveland Indians® 52 J.T. -

2017 Information & Record Book
2017 INFORMATION & RECORD BOOK OWNERSHIP OF THE CLEVELAND INDIANS Paul J. Dolan John Sherman Owner/Chairman/Chief Executive Of¿ cer Vice Chairman The Dolan family's ownership of the Cleveland Indians enters its 18th season in 2017, while John Sherman was announced as Vice Chairman and minority ownership partner of the Paul Dolan begins his ¿ fth campaign as the primary control person of the franchise after Cleveland Indians on August 19, 2016. being formally approved by Major League Baseball on Jan. 10, 2013. Paul continues to A long-time entrepreneur and philanthropist, Sherman has been responsible for establishing serve as Chairman and Chief Executive Of¿ cer of the Indians, roles that he accepted prior two successful businesses in Kansas City, Missouri and has provided extensive charitable to the 2011 season. He began as Vice President, General Counsel of the Indians upon support throughout surrounding communities. joining the organization in 2000 and later served as the club's President from 2004-10. His ¿ rst startup, LPG Services Group, grew rapidly and merged with Dynegy (NYSE:DYN) Paul was born and raised in nearby Chardon, Ohio where he attended high school at in 1996. Sherman later founded Inergy L.P., which went public in 2001. He led Inergy Gilmour Academy in Gates Mills. He graduated with a B.A. degree from St. Lawrence through a period of tremendous growth, merging it with Crestwood Holdings in 2013, University in 1980 and received his Juris Doctorate from the University of Notre Dame’s and continues to serve on the board of [now] Crestwood Equity Partners (NYSE:CEQP). -

Boston Red Sox (82-57) Vs
BOSTON RED SOX (82-57) VS. DETROIT TIGERS (81-57) Tuesday, September 3, 2013 • 7:10 p.m. ET • Fenway Park, Boston, MA LHP Jon Lester (12-8, 3.99) vs. RHP Max Scherzer (19-1, 2.90) Game #140 • Home Game #71 • TV: NESN/MLBN • Radio: WEEI 93.7 FM, WUFC 1510 AM (Spanish) STANDING TALL: Boston plays the 2nd of 3 games LESTER’S LAST 5: Tonight’s starter Jon Lester has quality against the Tigers tonight in the 3rd and fi nal series of a starts in his last 5 outings since 8/8...In that time, he ranks RED SOX RECORD BREAKDOWN Overall ........................................... 82-57 9-game homestand...The Sox are 5-2 thus far on the stand, 3rd in the AL in ERA (tied, 1.80) and opponent AVG (.198). AL East Standing ....................1st, 5.5 GA after taking 2 of 3 from Baltimore, sweeping the White Sox At Home ......................................... 45-25 in 3 games, and dropping last night’s series opener. PEN STRENGTH: The Red Sox bullpen has been charged On Road ......................................... 37-32 On the homestand, the Sox are outscoring opponents with runs in just 1 of 7 games during the current homes- In day games .................................. 25-13 37-22 with a .286 batting average and a 3.14 ERA. tand...In that time, Sox relievers have allowed just 2 runs In night games ............................... 57-44 and 8 hits over 18.2 innings (0.96 ERA). April ................................................. 18-8 Boston’s weekend sweep of the White Sox was the May ................................................ 15-15 club’s 1st sweep since 7/30-8/1 vs. -

07-02-2012 Red Sox Roster
Major League Roster (25) plus Disabled List (10) as of June 30, 2012 NUMERICAL ALPHABETICAL BY POSITION 2-Jacoby Ellsbury, OF* 91-Alfredo Aceves, RHP Coaching Staff 3-Mike Aviles, SS 32-Matt Albers, RHP 25-Bobby Valentine, Manager 5-Nick Punto, INF 48-Scott Atchison, RHP 17-Tim Bogar, Bench Coach 7-Cody Ross, OF 3-Mike Aviles, SS 22-Bob McClure, Pitching Coach 10-Kelly Shoppach, C 40-Andrew Bailey, RHP* 29-Dave Magadan, Hitting Coach 11-Clay Buchholz, RHP* 19-Josh Beckett, RHP 36-Alex Ochoa, First Base Coach 12-Ryan Sweeney, OF* 17-Tim Bogar, Bench Coach 43-Jerry Royster, Third Base Coach 13-Carl Crawford, OF* 11-Clay Buchholz, RHP* 57-Gary Tuck, Bullpen Coach 15-Dustin Pedroia, 2B -- -Chris Carpenter, RHP* 68-Randy Niemann, Asst. Pitching Coach 17-Tim Bogar, Bench Coach 35-Aaron Cook, RHP Pitchers (13+6 DL) 18-Daisuke Matsuzaka, RHP 13-Carl Crawford, OF* 11-Clay Buchholz, RHP* 19-Josh Beckett, RHP 61-Felix Doubront, LHP 18-Daisuke Matsuzaka, RHP 22-Bob McClure, Pitching Coach 2-Jacoby Ellsbury, OF* 19-Josh Beckett, RHP 23-Brent Lillibridge, INF/OF 28-Adrian Gonzalez, 1B 30-Andrew Miller, LHP 25-Bobby Valentine, Manager 53-Rich Hill, LHP* 31-Jon Lester, LHP 26-Scott Podsednik, OF* 52-Bobby Jenks, RHP* 32-Matt Albers, RHP 28-Adrian Gonzalez, 1B 55-Ryan Kalish, OF 35-Aaron Cook, RHP 29-Dave Magadan, Hitting Coach 41-John Lackey, RHP* 37-Mark Melancon, RHP 30-Andrew Miller, LHP 31-Jon Lester, LHP 40-Andrew Bailey, RHP* 31-Jon Lester, LHP 23-Brent Lillibridge, INF/OF 41-John Lackey, RHP* 32-Matt Albers, RHP 29-Dave Magadan, Hitting Coach -
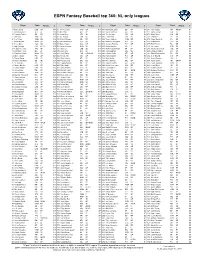
NL-Only Leagues
ESPN Fantasy Baseball top 360: NL-only leagues Player Team All pos. $ Player Team All pos. $ Player Team All pos. $ Player Team All pos. $ 1. Mookie Betts LAD OF $44 91. Joc Pederson CHC OF $14 181. MacKenzie Gore SD SP $7 271. John Curtiss MIA RP/SP $1 2. Ronald Acuna Jr. ATL OF $39 92. Will Smith ATL RP $14 182. Stefan Crichton ARI RP $6 272. Josh Fuentes COL 1B $1 3. Fernando Tatis Jr. SD SS $37 93. Austin Riley ATL 3B $14 183. Tim Locastro ARI OF $6 273. Wade Miley CIN SP $1 4. Juan Soto WSH OF $36 94. A.J. Pollock LAD OF $14 184. Lucas Sims CIN RP $6 274. Chad Kuhl PIT SP $1 5. Trea Turner WSH SS $32 95. Devin Williams MIL RP $13 185. Tanner Rainey WSH RP $6 275. Anibal Sanchez FA SP $1 6. Jacob deGrom NYM SP $30 96. German Marquez COL SP $13 186. Madison Bumgarner ARI SP $6 276. Rowan Wick CHC RP $1 7. Trevor Story COL SS $30 97. Raimel Tapia COL OF $13 187. Gregory Polanco PIT OF $6 277. Rick Porcello FA SP $0 8. Cody Bellinger LAD OF/1B $30 98. Carlos Carrasco NYM SP $13 188. Omar Narvaez MIL C $6 278. Jon Lester WSH SP $0 9. Freddie Freeman ATL 1B $29 99. Gavin Lux LAD 2B $13 189. Anthony DeSclafani SF SP $6 279. Antonio Senzatela COL SP $0 10. Christian Yelich MIL OF $29 100. Zach Eflin PHI SP $13 190. Josh Lindblom MIL SP $6 280. -

2010 AABA DRAFT LIST As of November 20, 2009
2010 AABA DRAFT LIST as of November 20, 2009 BATTERS (131) Nick Green - BOS Scott Podsednik - CWS Tyler Greene - STL Landon Powell - OAK Eliezer Alfonzo - SD Anthony Gwynn - SD Robb Quinlan - LAA Brandon Allen - ARI Wes Helms - FLA Humberto Quintero - HOU Robert Andino - BAL Diory Hernandez - ATL Cody Ransom - NYY Elvis Andrus - TEX Michel Hernandez - TB Colby Rasmus - STL MikeAubrey - BAL Koyie Hill - CHI Nolan Reimold - BAL Alex Avila - DET Paul Janish - CIN Ryan Roberts - ARI Jeff Bailey - BOS Jason Jaramillo - PIT Luis Rodriguez - SD Paul Bako - PHI Rob Johnson - SEA Alex Romero - ARI Brian Barden - STL Andruw Jones - TEX Adam Rosales - CIN Gordon Beckham - CWS Garrett Jones - PIT Randy Ruiz - TOR Brian Bixler - PIT Matt Kata - HOU Rusty Ryal - ARI Andres Blanco - CHI Don Kelly - DET Omir Santos - NY Kyle Blanks - SD Adam Kennedy - OAK Michael Saunders - SEA Willie Bloomquist - KC George Kottaras - BOS Bobby Scales - CHI Julio Borbon - TEX Matt LaPorta - CLE Jordan Schafer - ATL Michael Brantley - CLE Jason LaRue - STL Travis Snider - TOR Reid Brignac - TB Jeff Larish - DET Matt Stairs - PHI Chris Burke - SD Brent Lillibridge - CWS Drew Stubbs - CIN Everth Cabrera - SD Mitch Maier - KC Cory Sullivan - NY Brett Carroll - FLA Lou Marson - CLE Drew Sutton - CIN Juan Castro - LA Andy Marte - CLE Mike Sweeney - SEA Ronny Cedeno - PIT Gary Matthews - LAA Taylor Teagarden - TEX Francisco Cervelli - NYY Justin Maxwell - WSH Joe Thurston - STL Endy Chavez - SEA John Mayberry - PHI Matt Tolbert - MIN Raul Chavez - TOR Cameron Maybin - FLA Andres -

List of Players in Apba's 2018 Base Baseball Card
Sheet1 LIST OF PLAYERS IN APBA'S 2018 BASE BASEBALL CARD SET ARIZONA ATLANTA CHICAGO CUBS CINCINNATI David Peralta Ronald Acuna Ben Zobrist Scott Schebler Eduardo Escobar Ozzie Albies Javier Baez Jose Peraza Jarrod Dyson Freddie Freeman Kris Bryant Joey Votto Paul Goldschmidt Nick Markakis Anthony Rizzo Scooter Gennett A.J. Pollock Kurt Suzuki Willson Contreras Eugenio Suarez Jake Lamb Tyler Flowers Kyle Schwarber Jesse Winker Steven Souza Ender Inciarte Ian Happ Phillip Ervin Jon Jay Johan Camargo Addison Russell Tucker Barnhart Chris Owings Charlie Culberson Daniel Murphy Billy Hamilton Ketel Marte Dansby Swanson Albert Almora Curt Casali Nick Ahmed Rene Rivera Jason Heyward Alex Blandino Alex Avila Lucas Duda Victor Caratini Brandon Dixon John Ryan Murphy Ryan Flaherty David Bote Dilson Herrera Jeff Mathis Adam Duvall Tommy La Stella Mason Williams Daniel Descalso Preston Tucker Kyle Hendricks Luis Castillo Zack Greinke Michael Foltynewicz Cole Hamels Matt Harvey Patrick Corbin Kevin Gausman Jon Lester Sal Romano Zack Godley Julio Teheran Jose Quintana Tyler Mahle Robbie Ray Sean Newcomb Tyler Chatwood Anthony DeSclafani Clay Buchholz Anibal Sanchez Mike Montgomery Homer Bailey Matt Koch Brandon McCarthy Jaime Garcia Jared Hughes Brad Ziegler Daniel Winkler Steve Cishek Raisel Iglesias Andrew Chafin Brad Brach Justin Wilson Amir Garrett Archie Bradley A.J. Minter Brandon Kintzler Wandy Peralta Yoshihisa Hirano Sam Freeman Jesse Chavez David Hernandez Jake Diekman Jesse Biddle Pedro Strop Michael Lorenzen Brad Boxberger Shane Carle Jorge de la Rosa Austin Brice T.J. McFarland Jonny Venters Carl Edwards Jackson Stephens Fernando Salas Arodys Vizcaino Brian Duensing Matt Wisler Matt Andriese Peter Moylan Brandon Morrow Cody Reed Page 1 Sheet1 COLORADO LOS ANGELES MIAMI MILWAUKEE Charlie Blackmon Chris Taylor Derek Dietrich Lorenzo Cain D.J. -

Oakland Athletics Virtual Press
OAKLAND ATHLETICS Post Game Notes Oakland Athletics Baseball Company 7000 Coliseum Way Oakland, CA 94621 510-638-4900 Public Relations Facsimile 510-562-1633 www.oaklandathletics.com Texas Rangers (33-23) at Oakland Athletics (24-32) Tuesday, June 5, 2012 Oakland-Alameda County Coliseum 1 2 3 4 5 6 7 8 9 R H E LOB Texas 0 0 3 1 1 0 0 0 1 6 11 0 7 Oakland 0 0 0 0 2 1 0 0 0 3 9 0 9 W — Holland (5-4) L — Blackley (0-1) S — Nathan (12) OAKLAND NOTES The Oakland Athletics are 5-15 since May 15 after going 19-17 over the first 36 games of the season…have lost 14 of their last 18 games against the Rangers, including six of the last eight in Oakland… are 1-1 on this four-game homestand against Texas. Travis Blackley is 0-1 with a 4.66 ERA (5 er in 9.2 ip) in two starts this year and 0-0 with a 4.09 ERA (5 er in 11.0 ip) in seven relief appearances…is 1-4 with an 8.52 ERA (42 er in 44.1 ip) in 10 career starts. Sean Doolittle made his Major League debut and tossed 1.1 scoreless innings…struck out the first three batters he faced…the last A’s pitcher to strike out the first three batters he faced in his career was Blake Stein on May 10, 1998 against Chicago. Yoenis Cespedes (2 for 4) hit a home run in the sixth inning…is now batting .327 (17 for 52) with five of his six home runs at home compared to .200 (15 for 75) on the road.