19 64Apj. . .139.1105T a UEV STUDY of 94 WIDE VISUAL BINARIES
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Galaxies – AS 3011
Galaxies – AS 3011 Simon Driver [email protected] ... room 308 This is a Junior Honours 18-lecture course Lectures 11am Wednesday & Friday Recommended book: The Structure and Evolution of Galaxies by Steven Phillipps Galaxies – AS 3011 1 Aims • To understand: – What is a galaxy – The different kinds of galaxy – The optical properties of galaxies – The hidden properties of galaxies such as dark matter, presence of black holes, etc. – Galaxy formation concepts and large scale structure • Appreciate: – Why galaxies are interesting, as building blocks of the Universe… and how simple calculations can be used to better understand these systems. Galaxies – AS 3011 2 1 from 1st year course: • AS 1001 covered the basics of : – distances, masses, types etc. of galaxies – spectra and hence dynamics – exotic things in galaxies: dark matter and black holes – galaxies on a cosmological scale – the Big Bang • in AS 3011 we will study dynamics in more depth, look at other non-stellar components of galaxies, and introduce high-redshift galaxies and the large-scale structure of the Universe Galaxies – AS 3011 3 Outline of lectures 1) galaxies as external objects 13) large-scale structure 2) types of galaxy 14) luminosity of the Universe 3) our Galaxy (components) 15) primordial galaxies 4) stellar populations 16) active galaxies 5) orbits of stars 17) anomalies & enigmas 6) stellar distribution – ellipticals 18) revision & exam advice 7) stellar distribution – spirals 8) dynamics of ellipticals plus 3-4 tutorials 9) dynamics of spirals (questions set after -

Apparent and Absolute Magnitudes of Stars: a Simple Formula
Available online at www.worldscientificnews.com WSN 96 (2018) 120-133 EISSN 2392-2192 Apparent and Absolute Magnitudes of Stars: A Simple Formula Dulli Chandra Agrawal Department of Farm Engineering, Institute of Agricultural Sciences, Banaras Hindu University, Varanasi - 221005, India E-mail address: [email protected] ABSTRACT An empirical formula for estimating the apparent and absolute magnitudes of stars in terms of the parameters radius, distance and temperature is proposed for the first time for the benefit of the students. This reproduces successfully not only the magnitudes of solo stars having spherical shape and uniform photosphere temperature but the corresponding Hertzsprung-Russell plot demonstrates the main sequence, giants, super-giants and white dwarf classification also. Keywords: Stars, apparent magnitude, absolute magnitude, empirical formula, Hertzsprung-Russell diagram 1. INTRODUCTION The visible brightness of a star is expressed in terms of its apparent magnitude [1] as well as absolute magnitude [2]; the absolute magnitude is in fact the apparent magnitude while it is observed from a distance of . The apparent magnitude of a celestial object having flux in the visible band is expressed as [1, 3, 4] ( ) (1) ( Received 14 March 2018; Accepted 31 March 2018; Date of Publication 01 April 2018 ) World Scientific News 96 (2018) 120-133 Here is the reference luminous flux per unit area in the same band such as that of star Vega having apparent magnitude almost zero. Here the flux is the magnitude of starlight the Earth intercepts in a direction normal to the incidence over an area of one square meter. The condition that the Earth intercepts in the direction normal to the incidence is normally fulfilled for stars which are far away from the Earth. -

Spectroscopy of Variable Stars
Spectroscopy of Variable Stars Steve B. Howell and Travis A. Rector The National Optical Astronomy Observatory 950 N. Cherry Ave. Tucson, AZ 85719 USA Introduction A Note from the Authors The goal of this project is to determine the physical characteristics of variable stars (e.g., temperature, radius and luminosity) by analyzing spectra and photometric observations that span several years. The project was originally developed as a The 2.1-meter telescope and research project for teachers participating in the NOAO TLRBSE program. Coudé Feed spectrograph at Kitt Peak National Observatory in Ari- Please note that it is assumed that the instructor and students are familiar with the zona. The 2.1-meter telescope is concepts of photometry and spectroscopy as it is used in astronomy, as well as inside the white dome. The Coudé stellar classification and stellar evolution. This document is an incomplete source Feed spectrograph is in the right of information on these topics, so further study is encouraged. In particular, the half of the building. It also uses “Stellar Spectroscopy” document will be useful for learning how to analyze the the white tower on the right. spectrum of a star. Prerequisites To be able to do this research project, students should have a basic understanding of the following concepts: • Spectroscopy and photometry in astronomy • Stellar evolution • Stellar classification • Inverse-square law and Stefan’s law The control room for the Coudé Description of the Data Feed spectrograph. The spec- trograph is operated by the two The spectra used in this project were obtained with the Coudé Feed telescopes computers on the left. -

Gaia Data Release 2 Special Issue
A&A 623, A110 (2019) Astronomy https://doi.org/10.1051/0004-6361/201833304 & © ESO 2019 Astrophysics Gaia Data Release 2 Special issue Gaia Data Release 2 Variable stars in the colour-absolute magnitude diagram?,?? Gaia Collaboration, L. Eyer1, L. Rimoldini2, M. Audard1, R. I. Anderson3,1, K. Nienartowicz2, F. Glass1, O. Marchal4, M. Grenon1, N. Mowlavi1, B. Holl1, G. Clementini5, C. Aerts6,7, T. Mazeh8, D. W. Evans9, L. Szabados10, A. G. A. Brown11, A. Vallenari12, T. Prusti13, J. H. J. de Bruijne13, C. Babusiaux4,14, C. A. L. Bailer-Jones15, M. Biermann16, F. Jansen17, C. Jordi18, S. A. Klioner19, U. Lammers20, L. Lindegren21, X. Luri18, F. Mignard22, C. Panem23, D. Pourbaix24,25, S. Randich26, P. Sartoretti4, H. I. Siddiqui27, C. Soubiran28, F. van Leeuwen9, N. A. Walton9, F. Arenou4, U. Bastian16, M. Cropper29, R. Drimmel30, D. Katz4, M. G. Lattanzi30, J. Bakker20, C. Cacciari5, J. Castañeda18, L. Chaoul23, N. Cheek31, F. De Angeli9, C. Fabricius18, R. Guerra20, E. Masana18, R. Messineo32, P. Panuzzo4, J. Portell18, M. Riello9, G. M. Seabroke29, P. Tanga22, F. Thévenin22, G. Gracia-Abril33,16, G. Comoretto27, M. Garcia-Reinaldos20, D. Teyssier27, M. Altmann16,34, R. Andrae15, I. Bellas-Velidis35, K. Benson29, J. Berthier36, R. Blomme37, P. Burgess9, G. Busso9, B. Carry22,36, A. Cellino30, M. Clotet18, O. Creevey22, M. Davidson38, J. De Ridder6, L. Delchambre39, A. Dell’Oro26, C. Ducourant28, J. Fernández-Hernández40, M. Fouesneau15, Y. Frémat37, L. Galluccio22, M. García-Torres41, J. González-Núñez31,42, J. J. González-Vidal18, E. Gosset39,25, L. P. Guy2,43, J.-L. Halbwachs44, N. C. Hambly38, D. -

PHAS 1102 Physics of the Universe 3 – Magnitudes and Distances
PHAS 1102 Physics of the Universe 3 – Magnitudes and distances Brightness of Stars • Luminosity – amount of energy emitted per second – not the same as how much we observe! • We observe a star’s apparent brightness – Depends on: • luminosity • distance – Brightness decreases as 1/r2 (as distance r increases) • other dimming effects – dust between us & star Defining magnitudes (1) Thus Pogson formalised the magnitude scale for brightness. This is the brightness that a star appears to have on the sky, thus it is referred to as apparent magnitude. Also – this is the brightness as it appears in our eyes. Our eyes have their own response to light, i.e. they act as a kind of filter, sensitive over a certain wavelength range. This filter is called the visual band and is centred on ~5500 Angstroms. Thus these are apparent visual magnitudes, mv Related to flux, i.e. energy received per unit area per unit time Defining magnitudes (2) For example, if star A has mv=1 and star B has mv=6, then 5 mV(B)-mV(A)=5 and their flux ratio fA/fB = 100 = 2.512 100 = 2.512mv(B)-mv(A) where !mV=1 corresponds to a flux ratio of 1001/5 = 2.512 1 flux(arbitrary units) 1 6 apparent visual magnitude, mv From flux to magnitude So if you know the magnitudes of two stars, you can calculate mv(B)-mv(A) the ratio of their fluxes using fA/fB = 2.512 Conversely, if you know their flux ratio, you can calculate the difference in magnitudes since: 2.512 = 1001/5 log (f /f ) = [m (B)-m (A)] log 2.512 10 A B V V 10 = 102/5 = 101/2.5 mV(B)-mV(A) = !mV = 2.5 log10(fA/fB) To calculate a star’s apparent visual magnitude itself, you need to know the flux for an object at mV=0, then: mS - 0 = mS = 2.5 log10(f0) - 2.5 log10(fS) => mS = - 2.5 log10(fS) + C where C is a constant (‘zero-point’), i.e. -

Part 2 – Brightness of the Stars
5th Grade Curriculum Space Systems: Stars and the Solar System An electronic copy of this lesson in color that can be edited is available at the website below, if you click on Soonertarium Curriculum Materials and login in as a guest. The password is “soonertarium”. http://moodle.norman.k12.ok.us/course/index.php?categoryid=16 PART 2 – BRIGHTNESS OF THE STARS -PRELIMINARY MATH BACKGROUND: Students may need to review place values since this lesson uses numbers in the hundred thousands. There are two website links to online education games to review place values in the section. -ACTIVITY - HOW MUCH BIGGER IS ONE NUMBER THAN ANOTHER NUMBER? This activity involves having students listen to the sound that different powers of 10 of BBs makes in a pan, and dividing large groups into smaller groups so that students get a sense for what it means to say that 1,000 is 10 times bigger than 100. Astronomy deals with many big numbers, and so it is important for students to have a sense of what these numbers mean so that they can compare large distances and big luminosities. -ACTIVITY – WHICH STARS ARE THE BRIGHTEST IN THE SKY? This activity involves introducing the concepts of luminosity and apparent magnitude of stars. The constellation Canis Major was chosen as an example because Sirius has a much smaller luminosity but a much bigger apparent magnitude than the other stars in the constellation, which leads to the question what else effects the brightness of a star in the sky. -ACTIVITY – HOW DOES LOCATION AFFECT THE BRIGHTNESS OF STARS? This activity involves having the students test how distance effects apparent magnitude by having them shine flashlights at styrene balls at different distances. -

Variable Star
Variable star A variable star is a star whose brightness as seen from Earth (its apparent magnitude) fluctuates. This variation may be caused by a change in emitted light or by something partly blocking the light, so variable stars are classified as either: Intrinsic variables, whose luminosity actually changes; for example, because the star periodically swells and shrinks. Extrinsic variables, whose apparent changes in brightness are due to changes in the amount of their light that can reach Earth; for example, because the star has an orbiting companion that sometimes Trifid Nebula contains Cepheid variable stars eclipses it. Many, possibly most, stars have at least some variation in luminosity: the energy output of our Sun, for example, varies by about 0.1% over an 11-year solar cycle.[1] Contents Discovery Detecting variability Variable star observations Interpretation of observations Nomenclature Classification Intrinsic variable stars Pulsating variable stars Eruptive variable stars Cataclysmic or explosive variable stars Extrinsic variable stars Rotating variable stars Eclipsing binaries Planetary transits See also References External links Discovery An ancient Egyptian calendar of lucky and unlucky days composed some 3,200 years ago may be the oldest preserved historical document of the discovery of a variable star, the eclipsing binary Algol.[2][3][4] Of the modern astronomers, the first variable star was identified in 1638 when Johannes Holwarda noticed that Omicron Ceti (later named Mira) pulsated in a cycle taking 11 months; the star had previously been described as a nova by David Fabricius in 1596. This discovery, combined with supernovae observed in 1572 and 1604, proved that the starry sky was not eternally invariable as Aristotle and other ancient philosophers had taught. -

Astronomy General Information
ASTRONOMY GENERAL INFORMATION HERTZSPRUNG-RUSSELL (H-R) DIAGRAMS -A scatter graph of stars showing the relationship between the stars’ absolute magnitude or luminosities versus their spectral types or classifications and effective temperatures. -Can be used to measure distance to a star cluster by comparing apparent magnitude of stars with abs. magnitudes of stars with known distances (AKA model stars). Observed group plotted and then overlapped via shift in vertical direction. Difference in magnitude bridge equals distance modulus. Known as Spectroscopic Parallax. SPECTRA HARVARD SPECTRAL CLASSIFICATION (1-D) -Groups stars by surface atmospheric temp. Used in H-R diag. vs. Luminosity/Abs. Mag. Class* Color Descr. Actual Color Mass (M☉) Radius(R☉) Lumin.(L☉) O Blue Blue B Blue-white Deep B-W 2.1-16 1.8-6.6 25-30,000 A White Blue-white 1.4-2.1 1.4-1.8 5-25 F Yellow-white White 1.04-1.4 1.15-1.4 1.5-5 G Yellow Yellowish-W 0.8-1.04 0.96-1.15 0.6-1.5 K Orange Pale Y-O 0.45-0.8 0.7-0.96 0.08-0.6 M Red Lt. Orange-Red 0.08-0.45 *Very weak stars of classes L, T, and Y are not included. -Classes are further divided by Arabic numerals (0-9), and then even further by half subtypes. The lower the number, the hotter (e.g. A0 is hotter than an A7 star) YERKES/MK SPECTRAL CLASSIFICATION (2-D!) -Groups stars based on both temperature and luminosity based on spectral lines. -

Radial Velocity Variations in Red Giant Stars: Pulsations, Spots and Planets
RADIAL VELOCITY VARIATIONS IN RED GIANT STARS: PULSATIONS, SPOTS AND PLANETS RADIAL VELOCITY VARIATIONS IN RED GIANT STARS: PULSATIONS, SPOTS AND PLANETS Proefschrift ter verkrijging van de graad van Doctor aan de Universiteit Leiden, op gezag van de Rector Magnificus prof. mr. P. F. van der Heijden, volgens besluit van het College voor Promoties te verdedigen op 18 september 2007 klokke 13:45 uur door Saskia Hekker geboren te Heeze in 1978 Promotiecommissie Promotor: Prof. dr. A. Quirrenbach Sterrewacht Leiden Landessternwarte Heidelberg Promotor: Prof. dr. C. Aerts Katholieke Universiteit Leuven Radboud Universiteit Nijmegen Co-promotor: Dr. I. A. G. Snellen Sterrewacht Leiden Overige leden: Prof. dr. E. F. van Dishoeck Sterrewacht Leiden Prof. dr. K. H. Kuijken Sterrewacht Leiden Prof. dr. P. T. de Zeeuw Sterrewacht Leiden Dr. M. Hogerheijde Sterrewacht Leiden Dr. J. Lub Sterrewacht Leiden Dit proefschrift is tot stand gekomen met steun van No pain, no gain Contents 1 Introduction 1 1.1 Redgiantstars................................... 2 1.2 Observations ................................... 4 1.2.1 Iodinecell................................. 4 1.2.2 SimultaneousThAr............................ 4 1.3 Oscillations .................................... 5 1.3.1 Excitationmechanism .......................... 9 1.3.2 Asymptoticrelation. 10 1.3.3 Scalingrelations ............................. 10 1.4 Starspots...................................... 11 1.5 Sub-stellarcompanions . ... 12 1.6 Why can oscillations, spots and companions be observed as -

Stellar Masses
GENERAL I ARTICLE Stellar Masses B S Shylaja Introduction B S Shylaja is with the Bangalore Association for The twinkling diamonds in the night sky make us wonder at Science Education, which administers the their variety - while some are bright, some are faint; some are Jawaharlal Nehru blue and red. The attempt to understand this vast variety Planetarium as well as a eventually led to the physics of the structure of the stars. Science Centre. After obtaining her PhD on The brightness of a star is measured in magnitudes. Hipparchus, Wolf-Rayet stars from the a Greek astronomer who lived a hundred and fifty years before Indian Institute of Astrophysics, she Christ, devised the magnitude system that is still in use today continued research on for the measurement of the brightness of stars (and other celes novae, peculiar stars and tial bodies). Since the response of the human eye is logarithmic comets. She is also rather than linear in nature, the system of magnitudes based on actively engaged in teaching and writing visual estimates is on a logarithmic scale (Box 1). This scale was essays on scientific topics put on a quantitative basis by N R Pogson (he was the Director to reach students. of Madras Observatory) more than 150 years ago. The apparent magnitude does not take into account the distance of the star. Therefore, it does not give any idea of the intrinsic brightness of the star. If we could keep all the stars at the same 1 Parsec is a natural unit of dis distance, the apparent magnitude itself can give a measure of the tance used in astronomy. -
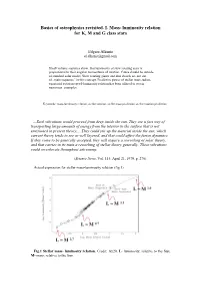
Basics of Astrophysics Revisited. I. Mass- Luminosity Relation for K, M and G Class Stars
Basics of astrophysics revisited. I. Mass- luminosity relation for K, M and G class stars Edgars Alksnis [email protected] Small volume statistics show, that luminosity of slow rotating stars is proportional to their angular momentums of rotation. Cause should be outside of standard solar model. Slow rotating giants and dim dwarfs are not out of „main sequence” in this concept. Predictive power of stellar mass-radius- equatorial rotation speed-luminosity relation has been offered to test in numerous examples. Keywords: mass-luminosity relation, stellar rotation, stellar mass prediction, stellar rotation prediction ...Such vibrations would proceed from deep inside the sun. They are a fast way of transporting large amounts of energy from the interior to the surface that is not envisioned in present theory.... They could stir up the material inside the sun, which current theory tends to see as well layered, and that could affect the fusion dynamics. If they come to be generally accepted, they will require a reworking of solar theory, and that carries in its train a reworking of stellar theory generally. These vibrations could reverberate throughout astronomy. (Science News, Vol. 115, April 21, 1979, p. 270). Actual expression for stellar mass-luminosity relation (fig.1) Fig.1 Stellar mass- luminosity relation. Credit: Ay20. L- luminosity, relative to the Sun, M- mass, relative to the Sun. remain empiric and in fact contain unresolvable contradiction: stellar luminosity basically is connected with their surface area (radius squared) but mass (radius in cube) appears as a factor which generate luminosity. That purely geometric difference had pressed astrophysicists to place several classes of stars outside of „main sequence” in the frame of their strange theoretic constructions. -
![Problem Set 6 Solutions [PDF]](https://docslib.b-cdn.net/cover/5509/problem-set-6-solutions-pdf-3315509.webp)
Problem Set 6 Solutions [PDF]
Astronomy 160: Frontiers and Controversies in Astrophysics Homework Set # 6 Solutions 1) a) Faint \brown-dwarf" stars have absolute magnitudes of around 17.5. How many times fainter than the Sun are these stars? MBD = 17:5 Msun = 5 − −5 b1 17:5 5 = 2 log b2 12:5×2 b1 −5 = log b2 − b1 5 = log b2 −5 b1 10 = b2 So brown dwarfs are 105 fainter than the sun. b) If one observes a nearby galaxy at a distance of 1 Mpc (= 106 parsecs) what is the apparent magnitude of Sun-like stars in that galaxy? distance = 106 parsecs − D m M = 5 log 10pc m − 5 = 5 log 105 m − 5 = 25 So the apparent magnitude of Sun-like stars at a distance of 106 parsecs is 30. c) The magnitude of the full Moon is around -14.5. How much brighter does the Sun appear than the Moon? The apparent magnitude of the full moon is -14.5. So we can use the brightness equation along with the apparent magnitude of the sun (-27) to find the ratio in brightnesses. − −5 b1 27 + 14:5 = 2 log b2 − × −2 b1 12:5 5 = 5 = log b2 b1 5 b2 = 10 The sun is 105 times brighter than the full moon. d) The brightest stars are around 105 times brighter than the Sun. If the apparent magnitude of these bright stars in some galaxy is 22.5, how far away is the galaxy? First we need to find the absolute magnitude of the bright stars. − −5 5 M1 5 = 2 log 10 −5 × − − M1 = 2 5 + 5 = 12:5 + 5 = 7:5 Now use the distance equation and the given apparent magnitude to find the dis- tance.