DOCSLIB.ORG

Sequences, Series and Taylor Approximation (Ma2712b, MA2730)

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Sequences, Series and Taylor Approximation (Ma2712b, MA2730) Sequences, Series and Taylor Approximation (MA2712b, MA2730) Level 2 Teaching Team Current curator: Simon Shaw November 20, 2015 Contents 0 Introduction, Overview 6 1 Taylor Polynomials 10 1.1 Lecture 1: Taylor Polynomials, Definition . .. 10 1.1.1 Reminder from Level 1 about Differentiable Functions . .. 11 1.1.2 Definition of Taylor Polynomials . 11 1.2 Lectures 2 and 3: Taylor Polynomials, Examples . ... 13 x 1.2.1 Example: Compute and plot Tnf for f(x) = e ............ 13 1.2.2 Example: Find the Maclaurin polynomials of f(x) = sin x ...... 14 2 1.2.3 Find the Maclaurin polynomial T11f for f(x) = sin(x ) ....... 15 1.2.4 QuestionsforChapter6: ErrorEstimates . 15 1.3 Lecture 4 and 5: Calculus of Taylor Polynomials . .. 17 1.3.1 GeneralResults............................... 17 1.4 Lecture 6: Various Applications of Taylor Polynomials . ... 22 1.4.1 RelativeExtrema .............................. 22 1.4.2 Limits .................................... 24 1.4.3 How to Calculate Complicated Taylor Polynomials? . 26 1.5 ExerciseSheet1................................... 29 1.5.1 ExerciseSheet1a .............................. 29 1.5.2 FeedbackforSheet1a ........................... 33 2 Real Sequences 40 2.1 Lecture 7: Definitions, Limit of a Sequence . ... 40 2.1.1 DefinitionofaSequence .......................... 40 2.1.2 LimitofaSequence............................. 41 2.1.3 Graphic Representations of Sequences . .. 43 2.2 Lecture 8: Algebra of Limits, Special Sequences . ..... 44 2.2.1 InfiniteLimits................................ 44 1 2.2.2 AlgebraofLimits.............................. 44 2.2.3 Some Standard Convergent Sequences . .. 46 2.3 Lecture 9: Bounded and Monotone Sequences . ..... 48 2.3.1 BoundedSequences............................. 48 2.3.2 Convergent Sequences and Closed Bounded Intervals . .... 48 2.4 Lecture10:MonotoneSequences . ... 49 2.4.1 Convergence of Monotone, Bounded Sequences . .... 50 2.5 ExerciseSheet2................................... 54 2.5.1 ExerciseSheet2a .............................. 54 2.5.2 FeedbackforSheet2a ........................... 56 3 A flipped classroom approach to Improper Integrals 58 3.1 Self-study for Lecture 11: Improper Integrals — Type 1 . ........ 58 3.2 Self-study for Lecture 11: Improper Integrals — Type 2 . ........ 61 3.3 Homeworkforimproperintegrals,Types1and2. .... 63 3.4 Feedback....................................... 64 3.4.1 Feedback on in-class exercises . 64 3.4.2 Homework feedback for improper integrals . 66 4 Real Series 78 4.1 Lecture12:Series.................................. 78 4.1.1 A Tale of a Rabbit and a Turtle following Zeno’s . 78 4.1.2 DefinitionofaSeries ............................ 79 4.1.3 Convergent Series, Geometric Series . 80 4.2 Lecture13:ImportantSeries. ... 83 4.2.1 ACriterionforDivergence .. .. .. 83 4.2.2 TelescopicSeries .............................. 84 4.2.3 HarmonicSeries............................... 85 4.2.4 AlgebraofSeries .............................. 86 4.3 Lecture14:TestforConvergence . .... 88 4.3.1 ComparisonTest .............................. 89 4.3.2 IntegralTest................................. 90 4.4 Lecture 15: Further Tests for Convergence . ....... 92 4.4.1 Comparing a Series with a Geometric Series: the Root and Ratio Tests 92 4.5 ExerciseSheet3................................... 96 4.5.1 ExerciseSheet3a .............................. 96 4.5.2 Additional Exercise Sheet 3b . 97 4.5.3 FeedbackforSheet3a ........................... 99 2 5 Deeper Results on Sequences and Series 103 5.1 Lecture 16: (ǫ, N)-DefinitionofLimits. .. .. 103 5.1.1 Practical Aspects of Estimates of Convergent Sequences . ....... 104 5.1.2 DivergentSequences ............................ 106 5.2 Extra curricular material: Error Estimates from the Tests . ........ 108 5.2.1 ErrorEstimatesfromtheRatioandRootTests . 108 5.2.2 ErrorEstimatesfortheIntegralTest . 108 5.3 Lecture 17: Absolute Convergence of Series and the Leibnitz Criterion of Con- vergence ....................................... 111 5.3.1 AlternatingSequences . .. .. .. 111 5.4 ExerciseSheet4................................... 116 5.4.1 ExerciseSheet4a .............................. 116 5.4.2 Additional Exercise Sheet 4b . 117 5.4.3 Short Feedback for Exercise Sheet 4a . 117 5.4.4 Short Feedback for the Additional Exercise Sheet 4b . 118 5.4.5 FeedbackforExerciseSheet4a . 119 6 Approximation with Taylor Polynomials 123 6.1 Lecture 18: Taylor’s theorem and errorestimates . ...... 123 6.2 TaylorTheorem................................... 124 6.3 Estimates Using Taylor Polynomial . 128 6.3.1 How to compute e inafewdecimalplaces?. 128 6.3.2 How good is the approximation of T4f for f(x) = cos(x)? ...... 129 6.3.3 Error in the Approximation sin x ≈ x .................. 130 6.4 EstimatingIntegrals ................................ 131 6.5 Extra curricular material: Estimating n for Taylor Polynomials . 135 6.6 ExerciseSheet5................................... 138 6.6.1 ExerciseSheet5a .............................. 138 6.6.2 ExerciseSheet5b.............................. 139 6.6.3 Miscellaneous Exercises . 140 6.6.4 FeedbackforExerciseSheet5a . 144 3 7 Power and Taylor Series 147 7.1 Lecture 19: About Taylor and Maclaurin Series . 147 7.1.1 Some Special Examples of Maclaurin Series . 147 7.1.2 Convergence Issues about Taylor Series . 148 7.1.3 Valid Taylor Series Expansions . 149 7.2 Lecture 20: Power Series, Radius of Convergence . ....... 151 7.2.1 Behaviour at the Boundary of the Interval of Convergence . ...... 153 7.2.2 Elementary Calculus of Taylor Series . 154 7.3 Lecture21: MoreonPowerandTaylorSeries . 155 7.3.1 TheBinomialTheorem........................... 157 7.4 Extra curricular material: General Theorem About Taylor Series ........ 159 7.4.1 Examples of Power Series Revisited . 160 7.4.2 Leibniz’ Formulas For ln 2 and π/4 .................... 161 7.5 Extra curricular material: Taylor Series and Fibonacci Numbers . ....... 163 7.5.1 Taylor Series in Number Theory . 163 7.5.2 Taylor’s Formula and Fibonacci Numbers . 164 7.5.3 MoreabouttheFibonacciNumbers . 165 7.6 Extra curricular Christmas treat: Series of Functions Can Be Difficult Objects 167 7.6.1 What Can Go ‘Wrong’ with Taylor Approximation? . 167 7.6.2 The Day That All Chemistry Stood Still . 168 7.6.3 Series Can Define Bizarre Functions: Continuous but Nowhere Differ- entiableFunctions ............................. 170 7.7 ExerciseSheet6................................... 172 7.7.1 ExerciseSheet6a .............................. 172 7.7.2 FeedbackforExerciseSheet6a . 175 7.7.3 Additional Exercise Sheet 6b . 180 7.7.4 ExerciseSheet0c .............................. 181 7.7.5 FeedbackforExerciseSheet0c. 183 4 List of Figures 1.1 The Maclaurin polynomials of degree 0, 1 and 2 of ex .............. 13 1.2 Maclaurin polynomials of ex andperturbations. 14 1.3 Maclaurin polynomials of sin x ........................... 15 x3 1.4 The graph near x =0 of g(x) = cos(x2) esin x ln(1 x) . ....... 24 − − − − 3 ( 1)n − 2.1 The first few values of a sequence alternating about the limit, like 1 + n . 43 2.2 The first few values of a sequence converging in a random fashion to the limiting cos n value, like 1 + n . ................................ 43 2.3 The first few values of a sequence increasing to 1, like (1 1 ). ........ 51 − n 1 2.4 The first few values of a sequence decreasing to 1, like (1 + n ). ........ 51 4.1 The area under the curve is less than the area under the line y = f(k 1) and − it is greater than the area under the line y = f(k). ............... 90 7.1 An innocent looking function with an unexpected Taylor series. ...... 169 7.2 Example (7.10) of a continuous nowhere differentiable real function ...... 170 5 Chapter 0 Introduction, Overview The first 12 lectures (Chapters 1-3) contribute to the study blocks MA2730 (for M, FM, MSM and MCS) and MA2712b (for MMS and MCC). Those blocks feed into the assessment blocks MA2812 and MA2815 (for M, FM, MSM and MCS) or MA2810 (for MMS and MCC). The purpose of those lectures is to make you familiar with important concepts in Calculus and Analysis, namely those of sequences and series as well as Taylor1 polynomials and series. In the first three chapters, you shall be introduced to elementary ideas about these concepts, so you could apprehend them as well as follow and perform relevant calculations. Students studying the full Analysis study block (MA2730) will continue, revisiting, broadening and deepening these concepts. In particular, you will be given the means to use more formal definitions and prove the results stated in the following first set of lectures. Most of Calculus (MA1711) and Fundamentals of Mathematics (MA1712) may be used in this set of lectures. For quick reference, we have put some essential background material of Level 1 in a revision section on Blackboard. You will have two lectures a week with one seminar (the class is split in four seminar groups). The 24 lectures are split into 6 chapters; each section of those chapters corresponding to a lecture. There will be one set of exercise sheets per chapter, obviously most of these sheets lasting for a few weeks. In Exercise Sheet number Na, N=1,..., 6, we expect to give you some short feedback first (to check your answers), finally rather detailed feedback. Additional exercises are given in Exercise Sheets Nb, N = 1,..., 6. Hence there will only be short feedback for them. Chapter 1 Taylor Polynomials (5 Lectures) Taylor polynomials are approximating a given differentiable function f, say, in a neighbour- hood of a given point x = a, say, by a polynomial
Load more

Recommended publications
  • ECE3040: Table of Contents
    ECE3040: Table of Contents Lecture 1: Introduction and Overview Instructor contact information Navigating the course web page What is meant by numerical methods? Example problems requiring numerical methods What is Matlab and why do we need it? Lecture 2: Matlab Basics I The Matlab environment Basic arithmetic calculations Command Window control & formatting Built-in constants & elementary functions Lecture 3: Matlab Basics II The assignment operator “=” for defining variables Creating and manipulating arrays Element-by-element array operations: The “.” Operator Vector generation with linspace function and “:” (colon) operator Graphing data and functions Lecture 4: Matlab Programming I Matlab scripts (programs) Input-output: The input and disp commands The fprintf command User-defined functions Passing functions to M-files: Anonymous functions Global variables Lecture 5: Matlab Programming II Making decisions: The if-else structure The error, return, and nargin commands Loops: for and while structures Interrupting loops: The continue and break commands Lecture 6: Programming Examples Plotting piecewise functions Computing the factorial of a number Beeping Looping vs vectorization speed: tic and toc commands Passing an “anonymous function” to Matlab function Approximation of definite integrals: Riemann sums Computing cos(푥) from its power series Stopping criteria for iterative numerical methods Computing the square root Evaluating polynomials Errors and Significant Digits Lecture 7: Polynomials Polynomials
    [Show full text]
  • Abel's Identity, 131 Abel's Test, 131–132 Abel's Theorem, 463–464 Absolute Convergence, 113–114 Implication of Condi
    INDEX Abel’s identity, 131 Bolzano-Weierstrass theorem, 66–68 Abel’s test, 131–132 for sequences, 99–100 Abel’s theorem, 463–464 boundary points, 50–52 absolute convergence, 113–114 bounded functions, 142 implication of conditional bounded sets, 42–43 convergence, 114 absolute value, 7 Cantor function, 229–230 reverse triangle inequality, 9 Cantor set, 80–81, 133–134, 383 triangle inequality, 9 Casorati-Weierstrass theorem, 498–499 algebraic properties of Rk, 11–13 Cauchy completeness, 106–107 algebraic properties of continuity, 184 Cauchy condensation test, 117–119 algebraic properties of limits, 91–92 Cauchy integral theorem algebraic properties of series, 110–111 triangle lemma, see triangle lemma algebraic properties of the derivative, Cauchy principal value, 365–366 244 Cauchy sequences, 104–105 alternating series, 115 convergence of, 105–106 alternating series test, 115–116 Cauchy’s inequalities, 437 analytic functions, 481–482 Cauchy’s integral formula, 428–433 complex analytic functions, 483 converse of, 436–437 counterexamples, 482–483 extension to higher derivatives, 437 identity principle, 486 for simple closed contours, 432–433 zeros of, see zeros of complex analytic on circles, 429–430 functions on open connected sets, 430–432 antiderivatives, 361 on star-shaped sets, 429 for f :[a, b] Rp, 370 → Cauchy’s integral theorem, 420–422 of complex functions, 408 consequence, see deformation of on star-shaped sets, 411–413 contours path-independence, 408–409, 415 Cauchy-Riemann equations Archimedean property, 5–6 motivation, 297–300
    [Show full text]
  • Methods of Measuring Population Change
    Methods of Measuring Population Change CDC 103 – Lecture 10 – April 22, 2012 Measuring Population Change • If past trends in population growth can be expressed in a mathematical model, there would be a solid justification for making projections on the basis of that model. • Demographers developed an array of models to measure population growth; four of these models are usually utilized. 1 Measuring Population Change Arithmetic (Linear), Geometric, Exponential, and Logistic. Arithmetic Change • A population growing arithmetically would increase by a constant number of people in each period. • If a population of 5000 grows by 100 annually, its size over successive years will be: 5100, 5200, 5300, . • Hence, the growth rate can be calculated by the following formula: • (100/5000 = 0.02 or 2 per cent). 2 Arithmetic Change • Arithmetic growth is the same as the ‘simple interest’, whereby interest is paid only on the initial sum deposited, the principal, rather than on accumulating savings. • Five percent simple interest on $100 merely returns a constant $5 interest every year. • Hence, arithmetic change produces a linear trend in population growth – following a straight line rather than a curve. Arithmetic Change 3 Arithmetic Change • The arithmetic growth rate is expressed by the following equation: Geometric Change • Geometric population growth is the same as the growth of a bank balance receiving compound interest. • According to this, the interest is calculated each year with reference to the principal plus previous interest payments, thereby yielding a far greater return over time than simple interest. • The geometric growth rate in demography is calculated using the ‘compound interest formula’.
    [Show full text]
  • Package 'Mosaiccalc'
    Package ‘mosaicCalc’ May 7, 2020 Type Package Title Function-Based Numerical and Symbolic Differentiation and Antidifferentiation Description Part of the Project MOSAIC (<http://mosaic-web.org/>) suite that provides utility functions for doing calculus (differentiation and integration) in R. The main differentiation and antidifferentiation operators are described using formulas and return functions rather than numerical values. Numerical values can be obtained by evaluating these functions. Version 0.5.1 Depends R (>= 3.0.0), mosaicCore Imports methods, stats, MASS, mosaic, ggformula, magrittr, rlang Suggests testthat, knitr, rmarkdown, mosaicData Author Daniel T. Kaplan <[email protected]>, Ran- dall Pruim <[email protected]>, Nicholas J. Horton <[email protected]> Maintainer Daniel Kaplan <[email protected]> VignetteBuilder knitr License GPL (>= 2) LazyLoad yes LazyData yes URL https://github.com/ProjectMOSAIC/mosaicCalc BugReports https://github.com/ProjectMOSAIC/mosaicCalc/issues RoxygenNote 7.0.2 Encoding UTF-8 NeedsCompilation no Repository CRAN Date/Publication 2020-05-07 13:00:13 UTC 1 2 D R topics documented: connector . .2 D..............................................2 findZeros . .4 fitSpline . .5 integrateODE . .5 numD............................................6 plotFun . .7 rfun .............................................7 smoother . .7 spliner . .7 Index 8 connector Create an interpolating function going through a set of points Description This is defined in the mosaic package: See connector. D Derivative and Anti-derivative operators Description Operators for computing derivatives and anti-derivatives as functions. Usage D(formula, ..., .hstep = NULL, add.h.control = FALSE) antiD(formula, ..., lower.bound = 0, force.numeric = FALSE) makeAntiDfun(.function, .wrt, from, .tol = .Machine$double.eps^0.25) numerical_integration(f, wrt, av, args, vi.from, ciName = "C", .tol) D 3 Arguments formula A formula.
    [Show full text]
  • Topic 7 Notes 7 Taylor and Laurent Series
    Topic 7 Notes Jeremy Orloff 7 Taylor and Laurent series 7.1 Introduction We originally defined an analytic function as one where the derivative, defined as a limit of ratios, existed. We went on to prove Cauchy's theorem and Cauchy's integral formula. These revealed some deep properties of analytic functions, e.g. the existence of derivatives of all orders. Our goal in this topic is to express analytic functions as infinite power series. This will lead us to Taylor series. When a complex function has an isolated singularity at a point we will replace Taylor series by Laurent series. Not surprisingly we will derive these series from Cauchy's integral formula. Although we come to power series representations after exploring other properties of analytic functions, they will be one of our main tools in understanding and computing with analytic functions. 7.2 Geometric series Having a detailed understanding of geometric series will enable us to use Cauchy's integral formula to understand power series representations of analytic functions. We start with the definition: Definition. A finite geometric series has one of the following (all equivalent) forms. 2 3 n Sn = a(1 + r + r + r + ::: + r ) = a + ar + ar2 + ar3 + ::: + arn n X = arj j=0 n X = a rj j=0 The number r is called the ratio of the geometric series because it is the ratio of consecutive terms of the series. Theorem. The sum of a finite geometric series is given by a(1 − rn+1) S = a(1 + r + r2 + r3 + ::: + rn) = : (1) n 1 − r Proof.
    [Show full text]
  • Math 142 – Quiz 6 – Solutions 1. (A) by Direct Calculation, Lim 1+3N 2
    Math 142 – Quiz 6 – Solutions 1. (a) By direct calculation, 1 + 3n 1 + 3 0 + 3 3 lim = lim n = = − . n→∞ n→∞ 2 2 − 5n n − 5 0 − 5 5 3 So it is convergent with limit − 5 . (b) By using f(x), where an = f(n), x2 2x 2 lim = lim = lim = 0. x→∞ ex x→∞ ex x→∞ ex (Obtained using L’Hˆopital’s Rule twice). Thus the sequence is convergent with limit 0. (c) By comparison, n − 1 n + cos(n) n − 1 ≤ ≤ 1 and lim = 1 n + 1 n + 1 n→∞ n + 1 n n+cos(n) o so by the Squeeze Theorem, the sequence n+1 converges to 1. 2. (a) By the Ratio Test (or as a geometric series), 32n+2 32n 3232n 7n 9 L = lim (16 )/(16 ) = lim = . n→∞ 7n+1 7n n→∞ 32n 7 7n 7 The ratio is bigger than 1, so the series is divergent. Can also show using the Divergence Test since limn→∞ an = ∞. (b) By the integral test Z ∞ Z t 1 1 t dx = lim dx = lim ln(ln x)|2 = lim ln(ln t) − ln(ln 2) = ∞. 2 x ln x t→∞ 2 x ln x t→∞ t→∞ So the integral diverges and thus by the Integral Test, the series also diverges. (c) By comparison, (n3 − 3n + 1)/(n5 + 2n3) n5 − 3n3 + n2 1 − 3n−2 + n−3 lim = lim = lim = 1. n→∞ 1/n2 n→∞ n5 + 2n3 n→∞ 1 + 2n−2 Since P 1/n2 converges (p-series, p = 2 > 1), by the Limit Comparison Test, the series converges.
    [Show full text]
  • 11.3-11.4 Integral and Comparison Tests
    11.3-11.4 Integral and Comparison Tests The Integral Test: Suppose a function f(x) is continuous, positive, and decreasing on [1; 1). Let an 1 P R 1 be defined by an = f(n). Then, the series an and the improper integral 1 f(x) dx either BOTH n=1 CONVERGE OR BOTH DIVERGE. Notes: • For the integral test, when we say that f must be decreasing, it is actually enough that f is EVENTUALLY ALWAYS DECREASING. In other words, as long as f is always decreasing after a certain point, the \decreasing" requirement is satisfied. • If the improper integral converges to a value A, this does NOT mean the sum of the series is A. Why? The integral of a function will give us all the area under a continuous curve, while the series is a sum of distinct, separate terms. • The index and interval do not always need to start with 1. Examples: Determine whether the following series converge or diverge. 1 n2 • X n2 + 9 n=1 1 2 • X n2 + 9 n=3 1 1 n • X n2 + 1 n=1 1 ln n • X n n=2 Z 1 1 p-series: We saw in Section 8.9 that the integral p dx converges if p > 1 and diverges if p ≤ 1. So, by 1 x 1 1 the Integral Test, the p-series X converges if p > 1 and diverges if p ≤ 1. np n=1 Notes: 1 1 • When p = 1, the series X is called the harmonic series. n n=1 • Any constant multiple of a convergent p-series is also convergent.
    [Show full text]
  • 3.3 Convergence Tests for Infinite Series
    3.3 Convergence Tests for Infinite Series 3.3.1 The integral test We may plot the sequence an in the Cartesian plane, with independent variable n and dependent variable a: n X The sum an can then be represented geometrically as the area of a collection of rectangles with n=1 height an and width 1. This geometric viewpoint suggests that we compare this sum to an integral. If an can be represented as a continuous function of n, for real numbers n, not just integers, and if the m X sequence an is decreasing, then an looks a bit like area under the curve a = a(n). n=1 In particular, m m+2 X Z m+1 X an > an dn > an n=1 n=1 n=2 For example, let us examine the first 10 terms of the harmonic series 10 X 1 1 1 1 1 1 1 1 1 1 = 1 + + + + + + + + + : n 2 3 4 5 6 7 8 9 10 1 1 1 If we draw the curve y = x (or a = n ) we see that 10 11 10 X 1 Z 11 dx X 1 X 1 1 > > = − 1 + : n x n n 11 1 1 2 1 (See Figure 1, copied from Wikipedia) Z 11 dx Now = ln(11) − ln(1) = ln(11) so 1 x 10 X 1 1 1 1 1 1 1 1 1 1 = 1 + + + + + + + + + > ln(11) n 2 3 4 5 6 7 8 9 10 1 and 1 1 1 1 1 1 1 1 1 1 1 + + + + + + + + + < ln(11) + (1 − ): 2 3 4 5 6 7 8 9 10 11 Z dx So we may bound our series, above and below, with some version of the integral : x If we allow the sum to turn into an infinite series, we turn the integral into an improper integral.
    [Show full text]
  • Calculus 141, Section 8.5 Symbolic Integration Notes by Tim Pilachowski
    Calculus 141, section 8.5 Symbolic Integration notes by Tim Pilachowski Back in my day (mid-to-late 1970s for high school and college) we had no handheld calculators, and the only electronic computers were mainframes at universities and government facilities. After learning the integration techniques that you are now learning, we were sent to Tables of Integrals, which listed results for (often) hundreds of simple to complicated integration results. Some could be evaluated using the methods of Calculus 1 and 2, others needed more esoteric methods. It was necessary to scan the Tables to find the form that was needed. If it was there, great! If not… The UMCP Physics Department posts one from the textbook they use (current as of 2017) at www.physics.umd.edu/hep/drew/IntegralTable.pdf . A similar Table of Integrals from http://www.had2know.com/academics/table-of-integrals-antiderivative-formulas.html is appended at the end of this Lecture outline. x 1 x Example F from 8.1: Evaluate e sindxx using a Table of Integrals. Answer : e ()sin x − cos x + C ∫ 2 If you remember, we had to define I, do a series of two integrations by parts, then solve for “ I =”. From the Had2Know Table of Integrals below: Identify a = and b = , then plug those values in, and voila! Now, with the development of handheld calculators and personal computers, much more is available to us, including software that will do all the work. The text mentions Derive, Maple, Mathematica, and MATLAB, and gives examples of Mathematica commands. You’ll be using MATLAB in Math 241 and several other courses.
    [Show full text]
  • 1 Approximating Integrals Using Taylor Polynomials 1 1.1 Definitions
    Seunghee Ye Ma 8: Week 7 Nov 10 Week 7 Summary This week, we will learn how we can approximate integrals using Taylor series and numerical methods. Topics Page 1 Approximating Integrals using Taylor Polynomials 1 1.1 Definitions . .1 1.2 Examples . .2 1.3 Approximating Integrals . .3 2 Numerical Integration 5 1 Approximating Integrals using Taylor Polynomials 1.1 Definitions When we first defined the derivative, recall that it was supposed to be the \instantaneous rate of change" of a function f(x) at a given point c. In other words, f 0 gives us a linear approximation of f(x) near c: for small values of " 2 R, we have f(c + ") ≈ f(c) + "f 0(c) But if f(x) has higher order derivatives, why stop with a linear approximation? Taylor series take this idea of linear approximation and extends it to higher order derivatives, giving us a better approximation of f(x) near c. Definition (Taylor Polynomial and Taylor Series) Let f(x) be a Cn function i.e. f is n-times continuously differentiable. Then, the n-th order Taylor polynomial of f(x) about c is: n X f (k)(c) T (f)(x) = (x − c)k n k! k=0 The n-th order remainder of f(x) is: Rn(f)(x) = f(x) − Tn(f)(x) If f(x) is C1, then the Taylor series of f(x) about c is: 1 X f (k)(c) T (f)(x) = (x − c)k 1 k! k=0 Note that the first order Taylor polynomial of f(x) is precisely the linear approximation we wrote down in the beginning.
    [Show full text]
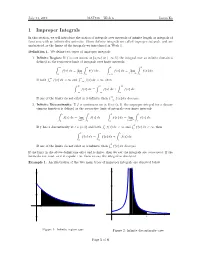
  • 1 Improper Integrals
    July 14, 2019 MAT136 { Week 6 Justin Ko 1 Improper Integrals In this section, we will introduce the notion of integrals over intervals of infinite length or integrals of functions with an infinite discontinuity. These definite integrals are called improper integrals, and are understood as the limits of the integrals we introduced in Week 1. Definition 1. We define two types of improper integrals: 1. Infinite Region: If f is continuous on [a; 1) or (−∞; b], the integral over an infinite domain is defined as the respective limit of integrals over finite intervals, Z 1 Z t Z b Z b f(x) dx = lim f(x) dx; f(x) dx = lim f(x) dx: a t!1 a −∞ t→−∞ t R 1 R a If both a f(x) dx < 1 and −∞ f(x) dx < 1, then Z 1 Z a Z 1 f(x) dx = f(x) dx + f(x) dx: −∞ −∞ a R 1 If one of the limits do not exist or is infinite, then −∞ f(x) dx diverges. 2. Infinite Discontinuity: If f is continuous on [a; b) or (a; b], the improper integral for a discon- tinuous function is defined as the respective limit of integrals over finite intervals, Z b Z t Z b Z b f(x) dx = lim f(x) dx f(x) dx = lim f(x) dx: a t!b− a a t!a+ t R c R b If f has a discontinuity at c 2 (a; b) and both a f(x) dx < 1 and c f(x) dx < 1, then Z b Z c Z b f(x) dx = f(x) dx + f(x) dx: a a c R b If one of the limits do not exist or is infinite, then a f(x) dx diverges.
    [Show full text]
  • Series: Convergence and Divergence Comparison Tests
    Series: Convergence and Divergence Here is a compilation of what we have done so far (up to the end of October) in terms of convergence and divergence. • Series that we know about: P∞ n Geometric Series: A geometric series is a series of the form n=0 ar . The series converges if |r| < 1 and 1 a1 diverges otherwise . If |r| < 1, the sum of the entire series is 1−r where a is the first term of the series and r is the common ratio. P∞ 1 2 p-Series Test: The series n=1 np converges if p1 and diverges otherwise . P∞ • Nth Term Test for Divergence: If limn→∞ an 6= 0, then the series n=1 an diverges. Note: If limn→∞ an = 0 we know nothing. It is possible that the series converges but it is possible that the series diverges. Comparison Tests: P∞ • Direct Comparison Test: If a series n=1 an has all positive terms, and all of its terms are eventually bigger than those in a series that is known to be divergent, then it is also divergent. The reverse is also true–if all the terms are eventually smaller than those of some convergent series, then the series is convergent. P P P That is, if an, bn and cn are all series with positive terms and an ≤ bn ≤ cn for all n sufficiently large, then P P if cn converges, then bn does as well P P if an diverges, then bn does as well. (This is a good test to use with rational functions.
    [Show full text]