A Note on Finite Groups with Few Values in a Column of the Character Table
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

NOTES on FINITE GROUP REPRESENTATIONS in Fall 2020, I
NOTES ON FINITE GROUP REPRESENTATIONS CHARLES REZK In Fall 2020, I taught an undergraduate course on abstract algebra. I chose to spend two weeks on the theory of complex representations of finite groups. I covered the basic concepts, leading to the classification of representations by characters. I also briefly addressed a few more advanced topics, notably induced representations and Frobenius divisibility. I'm making the lectures and these associated notes for this material publicly available. The material here is standard, and is mainly based on Steinberg, Representation theory of finite groups, Ch 2-4, whose notation I will mostly follow. I also used Serre, Linear representations of finite groups, Ch 1-3.1 1. Group representations Given a vector space V over a field F , we write GL(V ) for the group of bijective linear maps T : V ! V . n n When V = F we can write GLn(F ) = GL(F ), and identify the group with the group of invertible n × n matrices. A representation of a group G is a homomorphism of groups φ: G ! GL(V ) for some representation choice of vector space V . I'll usually write φg 2 GL(V ) for the value of φ on g 2 G. n When V = F , so we have a homomorphism φ: G ! GLn(F ), we call it a matrix representation. matrix representation The choice of field F matters. For now, we will look exclusively at the case of F = C, i.e., representations in complex vector spaces. Remark. Since R ⊆ C is a subfield, GLn(R) is a subgroup of GLn(C). -

Molecular Symmetry
Molecular Symmetry Symmetry helps us understand molecular structure, some chemical properties, and characteristics of physical properties (spectroscopy) – used with group theory to predict vibrational spectra for the identification of molecular shape, and as a tool for understanding electronic structure and bonding. Symmetrical : implies the species possesses a number of indistinguishable configurations. 1 Group Theory : mathematical treatment of symmetry. symmetry operation – an operation performed on an object which leaves it in a configuration that is indistinguishable from, and superimposable on, the original configuration. symmetry elements – the points, lines, or planes to which a symmetry operation is carried out. Element Operation Symbol Identity Identity E Symmetry plane Reflection in the plane σ Inversion center Inversion of a point x,y,z to -x,-y,-z i Proper axis Rotation by (360/n)° Cn 1. Rotation by (360/n)° Improper axis S 2. Reflection in plane perpendicular to rotation axis n Proper axes of rotation (C n) Rotation with respect to a line (axis of rotation). •Cn is a rotation of (360/n)°. •C2 = 180° rotation, C 3 = 120° rotation, C 4 = 90° rotation, C 5 = 72° rotation, C 6 = 60° rotation… •Each rotation brings you to an indistinguishable state from the original. However, rotation by 90° about the same axis does not give back the identical molecule. XeF 4 is square planar. Therefore H 2O does NOT possess It has four different C 2 axes. a C 4 symmetry axis. A C 4 axis out of the page is called the principle axis because it has the largest n . By convention, the principle axis is in the z-direction 2 3 Reflection through a planes of symmetry (mirror plane) If reflection of all parts of a molecule through a plane produced an indistinguishable configuration, the symmetry element is called a mirror plane or plane of symmetry . -

GROUP REPRESENTATIONS and CHARACTER THEORY Contents 1
GROUP REPRESENTATIONS AND CHARACTER THEORY DAVID KANG Abstract. In this paper, we provide an introduction to the representation theory of finite groups. We begin by defining representations, G-linear maps, and other essential concepts before moving quickly towards initial results on irreducibility and Schur's Lemma. We then consider characters, class func- tions, and show that the character of a representation uniquely determines it up to isomorphism. Orthogonality relations are introduced shortly afterwards. Finally, we construct the character tables for a few familiar groups. Contents 1. Introduction 1 2. Preliminaries 1 3. Group Representations 2 4. Maschke's Theorem and Complete Reducibility 4 5. Schur's Lemma and Decomposition 5 6. Character Theory 7 7. Character Tables for S4 and Z3 12 Acknowledgments 13 References 14 1. Introduction The primary motivation for the study of group representations is to simplify the study of groups. Representation theory offers a powerful approach to the study of groups because it reduces many group theoretic problems to basic linear algebra calculations. To this end, we assume that the reader is already quite familiar with linear algebra and has had some exposure to group theory. With this said, we begin with a preliminary section on group theory. 2. Preliminaries Definition 2.1. A group is a set G with a binary operation satisfying (1) 8 g; h; i 2 G; (gh)i = g(hi)(associativity) (2) 9 1 2 G such that 1g = g1 = g; 8g 2 G (identity) (3) 8 g 2 G; 9 g−1 such that gg−1 = g−1g = 1 (inverses) Definition 2.2. -

Representations, Character Tables, and One Application of Symmetry Chapter 4
Representations, Character Tables, and One Application of Symmetry Chapter 4 Friday, October 2, 2015 Matrices and Matrix Multiplication A matrix is an array of numbers, Aij column columns matrix row matrix -1 4 3 1 1234 rows -8 -1 7 2 2141 3 To multiply two matrices, add the products, element by element, of each row of the first matrix with each column in the second matrix: 12 12 (1×1)+(2×3) (1×2)+(2×4) 710 × 34 34 = (3×1)+(4×3) (3×2)+(4×4) = 15 22 100 1 1 0-10× 2 = -2 002 3 6 Transformation Matrices Each symmetry operation can be represented by a 3×3 matrix that shows how the operation transforms a set of x, y, and z coordinates y Let’s consider C2h {E, C2, i, σh}: x transformation matrix C2 x’ = -x -1 0 0 x’ -1 0 0 x -x y’ = -y 0-10 y’ ==0-10 y -y z’ = z 001 z’ 001 z z new transformation old new in terms coordinates ==matrix coordinates of old transformation i matrix x’ = -x -1 0 0 x’ -1 0 0 x -x y’ = -y 0-10 y’ ==0-10 y -y z’ = -z 00-1 z’ 00-1z -z Representations of Groups The set of four transformation matrices forms a matrix representation of the C2h point group. 100 -1 0 0 -1 0 0 100 E: 010 C2: 0-10 i: 0-10 σh: 010 001 001 00-1 00-1 These matrices combine in the same way as the operations, e.g., -1 0 0 -1 0 0 100 C2 × C2 = 0-10 0-10= 010= E 001001 001 The sum of the numbers along each matrix diagonal (the character) gives a shorthand version of the matrix representation, called Γ: C2h EC2 i σh Γ 3-1-31 Γ (gamma) is a reducible representation b/c it can be further simplified. -

Lecture Notes
i Applications of Group Theory to the Physics of Solids M. S. Dresselhaus 8.510J 6.734J SPRING 2002 ii Contents 1 Basic Mathematical Background 1 1.1 De¯nition of a Group . 1 1.2 Simple Example of a Group . 2 1.3 Basic De¯nitions . 4 1.4 Rearrangement Theorem . 6 1.5 Cosets . 6 1.6 Conjugation and Class . 8 1.6.1 Self-Conjugate Subgroups . 9 1.7 Factor Groups . 10 1.8 Selected Problems . 11 2 Representation Theory 15 2.1 Important De¯nitions . 15 2.2 Matrices . 17 2.3 Irreducible Representations . 18 2.4 The Unitarity of Representations . 20 2.5 Schur's Lemma (Part I) . 23 2.6 Schur's Lemma (Part 2) . 24 2.7 Wonderful Orthogonality Theorem . 27 2.8 Representations and Vector Spaces . 30 2.9 Suggested Problems . 31 3 Character of a Representation 33 3.1 De¯nition of Character . 33 3.2 Characters and Class . 34 3.3 Wonderful Orthogonality Theorem for Character . 36 3.4 Reducible Representations . 38 iii iv CONTENTS 3.5 The Number of Irreducible Representations . 40 3.6 Second Orthogonality Relation for Characters . 41 3.7 Regular Representation . 43 3.8 Setting up Character Tables . 47 3.9 Symmetry Notation . 51 3.10 Selected Problems . 73 4 Basis Functions 75 4.1 Symmetry Operations and Basis Functions . 75 4.2 Basis Functions for Irreducible Representations . 77 ^(¡n) 4.3 Projection Operators Pkl . 82 ^(¡n) 4.4 Derivation of Pk` . 83 4.5 Projection Operations on an Arbitrary Function . 84 4.6 Linear Combinations for 3 Equivalent Atoms . -

The Q-Conjugacy Character Table of Dihedral Groups
ITALIAN JOURNAL OF PURE AND APPLIED MATHEMATICS { N. 39{2018 (89{96) 89 THE Q-CONJUGACY CHARACTER TABLE OF DIHEDRAL GROUPS H. Shabani A. R. Ashrafi E. Haghi Department of Pure Mathematics Faculty of Mathematical Sciences University of Kashan P.O. Box 87317-53153 Kashan I.R. Iran M. Ghorbani∗ Department of Pure Mathematics Faculty of Sciences Shahid Rajaee Teacher Training University P.O. Box 16785-136 Tehran I.R. Iran [email protected] Abstract. In a seminal paper published in 1998, Shinsaku Fujita introduced the concept of Q-conjugacy character table of a finite group. He applied this notion to solve some problems in combinatorial chemistry. In this paper, the Q-conjugacy character table of dihedral groups is computed in general. As a consequence, Q- ∼ ∼ conjugacy character table of molecules with point group symmetries D = C = Dih , ∼ ∼ ∼ ∼ ∼ ∼ ∼ ∼3 3v∼ 6 D = D = C = Dih , D = C = Dih , D = D = D = C = Dih , 4 ∼ 2d ∼ 4v ∼ 8 5 ∼5v 10 ∼3d ∼3h 6 ∼6v 12 D2 = C2v = Z2 × Z2 = Dih2, D4d = Dih16, D5d = D5h = Dih20, D6d = Dih24 are computed, where Z2 denotes a cyclic group of order 2 and Dihn is the dihedral group of even order n. Keywords: Q-conjugacy character table, dihedral group, conjugacy class. 1. Introduction A representation of a group G is a homomorphism from G into the group of invertible operators of a vector space V . In this case, we can interpret each element of G as an invertible linear transformation V −! V . If n = dimV and fix a basis for V then we can construct an isomorphism between the set of all \invertible linear transformation V −! V " and the set of all \invertible n × n matrices". -

Irreducible Representations and Character Tables
MIT OpenCourseWare http://ocw.mit.edu 5.04 Principles of Inorganic Chemistry II �� Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 5.04, Principles of Inorganic Chemistry II Prof. Daniel G. Nocera Lecture 3: Irreducible Representations and Character Tables Similarity transformations yield irreducible representations, Γi, which lead to the useful tool in group theory – the character table. The general strategy for determining Γi is as follows: A, B and C are matrix representations of symmetry operations of an arbitrary basis set (i.e., elements on which symmetry operations are performed). There is some similarity transform operator v such that A’ = v –1 ⋅ A ⋅ v B’ = v –1 ⋅ B ⋅ v C’ = v –1 ⋅ C ⋅ v where v uniquely produces block-diagonalized matrices, which are matrices possessing square arrays along the diagonal and zeros outside the blocks ⎡ A1 ⎤ ⎡B1 ⎤ ⎡C1 ⎤ ′ = ⎢ ⎥ ′ = ⎢ ⎥ ′ = ⎢ ⎥ A ⎢ A 2 ⎥ B ⎢ B2 ⎥ C ⎢ C 2 ⎥ ⎢ A ⎥ ⎢ B ⎥ ⎢ C ⎥ ⎣ 3 ⎦ ⎣ 3 ⎦ ⎣ 3 ⎦ Matrices A, B, and C are reducible. Sub-matrices Ai, Bi and Ci obey the same multiplication properties as A, B and C. If application of the similarity transform does not further block-diagonalize A’, B’ and C’, then the blocks are irreducible representations. The character is the sum of the diagonal elements of Γi. 2 As an example, let’s continue with our exemplary group: E, C3, C3 , σv, σv’, σv” by defining an arbitrary basis … a triangle v A v'' v' C B The basis set is described by the triangles vertices, points A, B and C. -

A Point Group Character Tables
A Point Group Character Tables Appendix A contains Point Group Character (Tables A.1–A.34) to be used throughout the chapters of this book. Pedagogic material to assist the reader in the use of these character tables can be found in Chap. 3. The Schoenflies symmetry (Sect. 3.9) and Hermann–Mauguin notations (Sect. 3.10) for the point groups are also discussed in Chap. 3. Some of the more novel listings in this appendix are the groups with five- fold symmetry C5, C5h, C5v, D5, D5d, D5h, I, Ih. The cubic point group Oh in Table A.31 lists basis functions for all the irreducible representations of Oh and uses the standard solid state physics notation for the irreducible representations. Table A.1. Character table for group C1 (triclinic) C1 (1) E A 1 Table A.2. Character table for group Ci = S2 (triclinic) S2 (1) Ei 2 2 2 x ,y ,z ,xy,xz,yz Rx,Ry,Rz Ag 11 x, y, z Au 1 −1 Table A.3. Character table for group C1h = S1 (monoclinic) C1h(m) Eσh 2 2 2 x ,y ,z ,xy Rz,x,y A 11 xz, yz Rx,Ry,z A 1 −1 480 A Point Group Character Tables Table A.4. Character table for group C2 (monoclinic) C2 (2) EC2 2 2 2 x ,y ,z ,xy Rz,z A 11 (x, y) xz, yz B 1 −1 (Rx,Ry) Table A.5. Character table for group C2v (orthorhombic) C2v (2mm) EC2 σv σv 2 2 2 x ,y ,z z A1 1111 xy Rz A2 11−1 −1 xz Ry,x B1 1 −11−1 yz Rx,y B2 1 −1 −11 Table A.6. -

Symmetry in Condensed Matter Physics Group and Representation Theory Lectures 1-8 Paolo G
Symmetry in Condensed Matter Physics Group and representation theory Lectures 1-8 Paolo G. Radaelli, Clarendon Laboratory, Oxford University Bibliography ◦ Volker Heine Group Theory in Quantum Mechanics, Dover Publication Press, 1993. A very popular book on the applications of group theory to quantum mechanics. ◦ M.S. Dresselhaus, G. Dresselhaus and A. Jorio, Group Theory - Application to the Physics of Condensed Matter, Springer-Verlag Berlin Heidelberg (2008). A recent book on irre- ducible representation theory and its application to a variety of physical problems. It should also be available on line free of charge from Oxford accounts. ◦ T. Hahn, ed., International tables for crystallography, vol. A (Kluver Academic Publisher, Dodrecht: Holland/Boston: USA/ London: UK, 2002), 5th ed. The International Tables for Crystallography are an indispensable text for any condensed-matter physicist. It currently consists of 8 volumes. A selection of pages is provided on the web site. Additional sample pages can be found on http://www.iucr.org/books/international-tables. ◦ J.F. Nye Physical properties of crystals, Clarendon Press, Oxford 2004. A very complete book about physical properties and tensors. It employs a rather traditional formalism, but it is well worth reading and consulting. Additional texts ◦ C. Hammond The Basics of Crystallography and Diffraction, Oxford University Press (from Blackwells). A well-established textbook for crystallography and diffraction. ◦ Paolo G. Radaelli, Symmetry in Crystallography: Understanding the International Tables, Oxford University Press (2011). An introduction to symmetry in the International Tables. ◦ C. Giacovazzo, H.L. Monaco, D. Viterbo, F. Scordari, G. Gilli, G. Zanotti and M. Catti, Fun- damentals of crystallography , nternational Union of Crystallography, Oxford University Press Inc., New York. -

Some Moonshine Connections Between Fischer-Griess Monster Group () and Number Theory
The International Journal Of Engineering And Science (IJES) || Volume || 3 || Issue || 5 || Pages || 25-36 || 2014 || ISSN (e): 2319 – 1813 ISSN (p): 2319 – 1805 Some Moonshine connections between Fischer-Griess Monster group () and Number theory Amina Muhammad Lawan Department of Mathematical sciences, Faculty of science, Bayero University, Kano, Nigeria. ------------------------------------------------------------ABSTRACT--------------------------------------------------------- This paper investigates moonshine connections between the McKay –Thompson series of some conjugacy classes for the monster group and number theory. We explore certain natural consequences of the Mckay- Thompson series of class 1A, 2A and 3A for the monster group in Ramanujan-type Pi formulas. Numerical results show that, the quadratic prime-generating polynomials are connected to integer values of exactly 43 Mc Kay- Thompson series of the conjugacy classes for the monster group. Furthermore, the transcendental number pi is approximated from monster group. Keywords: Fischer-Griess monster group, Monstrous moonshine, Mc Kay- Thompson series, prime-generating polynomial, Fundamental discriminant, Ramanujan-type pi formulas. --------------------------------------------------------------------------------------------------------------------------------------- Date of Submission: 05 April 2014 Date of Publication: 30 May 2014 --------------------------------------------------------------------------------------------------------------------------------------------------- I. INTRODUCTION The Fischer-Griess monster group is the largest and the most popular among the twenty six sporadic finite simple groups of order 246 3 20 5 9 7 6 9 7 11 2 13 3 17 19 23 29 31 41 47 59 71 53 8080,17424,79451,28758,86459,90496,17107,57005,75436,80000,00000 8 10 . In late 1973 Bernd Fischer and Robert Griess independently produced evidence for its existence. Conway and Norton [6] proposed to call this group the Monster and conjectured that it had a representation of dimension196,883 47 59 71. -

On the Action of the Sporadic Simple Baby Monster Group on Its Conjugacy Class 2B
London Mathematical Society ISSN 1461–1570 ON THE ACTION OF THE SPORADIC SIMPLE BABY MONSTER GROUP ON ITS CONJUGACY CLASS 2B JURGEN¨ MULLER¨ Abstract We determine the character table of the endomorphism ring of the permutation module associated with the multiplicity- free action of the sporadic simple Baby Monster group B on its conjugacy class 2B, where the centraliser of a 2B-element 1+22 is a maximal subgroup of shape 2 .Co2.Thisisoneofthe first applications of a new general computational technique to enumerate big orbits. 1. Introduction The aim of the present work is to determine the character table of the endomorphism ring of the permutation module associated with the multiplicity-free action of the Baby Monster group B, the second largest of the sporadic simple groups, on its conjugacy class 2B, where the centraliser of a 2B-element is a maximal subgroup 1+22 of shape 2 .Co2. The final result is given in Table 4. In general, the endomorphism ring of a permutation module reflects aspects of the representation theory of the underlying group. Its character table in particular encodes information about the spectral properties of the orbital graphs associated with the permutation action, such as distance-transitivity or distance-regularity, see [14, 5], or the Ramanujan property, see [7]. Here multiplicity-free actions, that is those whose associated endomorphism ring is commutative, have been of particular interest; for example a distance-transitive graph necessarily is an orbital graph associated with a multiplicity-free action. The multiplicity-free permutation actions of the sporadic simple groups and the related almost quasi-simple groups have been classified in [3, 16, 2], and the as- sociated character tables including the one presented here have been collected in [4, 20]. -
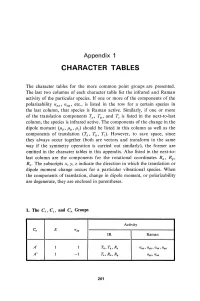
Character Tables
Appendix 1 CHARACTER TABLES The character tables for the more common point groups are presented. The last two columns of each character table list the infrared and Raman activity of the particular species. If one or more of the components of the polarizability a xx , a xy ' etc., is listed in the row for a certain species in the last column, that species is Raman active. Similarly, if one or more of the translation components Tz, T y , and Tz is listed in the next-to-last column, the species is infrared active. The components of the change in the dipole moment (/hz, /hy' /hz) should be listed in this column as wen as the components of translation (Tz, Ty, Tz). However, to save space, since they always occur together (both are vectors and transform in the same way if the symmetry operation is carried out similarly), the former are omitted in the character tables in this appendix. Also listed in the next-to last column are the components for the rotational coordinates Rz ' Ry , Rz • The subscripts x, y, z indicate the direction in which the translation or dipole moment change occurs for a particular vibrational species. When the components of translation, change in dipole moment, or polarizability are degenerate, they are enclosed in parentheses. 1. Tbe Cs , Ci' and Cn Groups Activity C. E (J",y IR Raman A' 1 1 T"" Ty, Rz axx , Ct.V1J , azz , Ct.a;1I A" 1 -1 Tz, R"" Ry Ct.1IZ , a xz 201 202 Appendix 1 Activity Ci E i IR Raman Ag 1 1 R x , R y, R.