(Batter|Pitcher)2Vec: Statistic-Free Talent Modeling with Neural Player Embeddings
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Dayton Baseball
DAYTON BASEBALL 2020 RECORD BOOK RECORD BOOK (THROUGH 2020) Team Records (single-season) Batting Individual Records Pitching Indivudual Records MLB Draft Awards RECORD BOOK (THROUGH 2020) DAYTON BASEBALL TEAM RECORDS BATTING RUNS BATTED IN PITCHING FEWEST EARNED RUNS ALLOWED 1 2009 . 448 1 1998 . 222 BATTING AVERAGE COMPLETE GAMES 2 2003 . 389 2 2008 . 229 1 2009 . .332 1 1992 . 21 3 2002 . 361 3 2011 . 231 2 1998 . .317 2 2005 . 18 4 2005 . 358 4 1993 . 256 3 1966 . .309 2001 . 18 5 2010 . 349 5 2006 . 258 4 2005 . .308 2000 . 18 6 2012 . 335 6 2004 . 262 5 2000 . .305 5 1991 . 16 7 2000 . 329 * 2020 . 72 6 1986 . .302 6 1987 . 15 8 2001 . 325 7 2002 . .301 1971 . 15 9 2019 . 315 MOST EARNED RUNS ALLOWED 8 1993 . .299 * 2020 . 0 10 2004 . 303 1 1993 . 389 * 2020 . .272 * 2020 . 83 2 1995 . 380 INNINGS PITCHED 3 1989 . 378 1 2012 . 549 .1 DOUBLES 4 1990 . 355 AT-BATS 2 2011 . 528 .1 1 2009 . 143 5 1994 . 349 1 2012 . 2,183 3 2019 . 522 .2 2 2010 . 131 * 2020 . 72 2 2011 . 2,043 4 2009 . 494 .1 3 1993 . 125 3 2009 . 2,005 5 2006 . 488 .0 4 2006 . 115 STRIKEOUTS 4 2019 . 2,004 6 2008 . 485 .2 5 2011 . 119 1 2019 . 491 5 1993 . 1,989 7 2017 . 484 .1 6 2014 . 109 2 2011 . 429 6 2010 . 1,967 8 2010 . 480 .2 7 2012 . 104 3 2012 . 381 7 2005 . 1,932 9 2007 . -

Tml American - Single Season Leaders 1954-2016
TML AMERICAN - SINGLE SEASON LEADERS 1954-2016 AVERAGE (496 PA MINIMUM) RUNS CREATED HOMERUNS RUNS BATTED IN 57 ♦MICKEY MANTLE .422 57 ♦MICKEY MANTLE 256 98 ♦MARK McGWIRE 75 61 ♦HARMON KILLEBREW 221 57 TED WILLIAMS .411 07 ALEX RODRIGUEZ 235 07 ALEX RODRIGUEZ 73 16 DUKE SNIDER 201 86 WADE BOGGS .406 61 MICKEY MANTLE 233 99 MARK McGWIRE 72 54 DUKE SNIDER 189 80 GEORGE BRETT .401 98 MARK McGWIRE 225 01 BARRY BONDS 72 56 MICKEY MANTLE 188 58 TED WILLIAMS .392 61 HARMON KILLEBREW 220 61 HARMON KILLEBREW 70 57 TED WILLIAMS 187 61 NORM CASH .391 01 JASON GIAMBI 215 61 MICKEY MANTLE 69 98 MARK McGWIRE 185 04 ICHIRO SUZUKI .390 09 ALBERT PUJOLS 214 99 SAMMY SOSA 67 07 ALEX RODRIGUEZ 183 85 WADE BOGGS .389 61 NORM CASH 207 98 KEN GRIFFEY Jr. 67 93 ALBERT BELLE 183 55 RICHIE ASHBURN .388 97 LARRY WALKER 203 3 tied with 66 97 LARRY WALKER 182 85 RICKEY HENDERSON .387 00 JIM EDMONDS 203 94 ALBERT BELLE 182 87 PEDRO GUERRERO .385 71 MERV RETTENMUND .384 SINGLES DOUBLES TRIPLES 10 JOSH HAMILTON .383 04 ♦ICHIRO SUZUKI 230 14♦JONATHAN LUCROY 71 97 ♦DESI RELAFORD 30 94 TONY GWYNN .383 69 MATTY ALOU 206 94 CHUCK KNOBLAUCH 69 94 LANCE JOHNSON 29 64 RICO CARTY .379 07 ICHIRO SUZUKI 205 02 NOMAR GARCIAPARRA 69 56 CHARLIE PEETE 27 07 PLACIDO POLANCO .377 65 MAURY WILLS 200 96 MANNY RAMIREZ 66 79 GEORGE BRETT 26 01 JASON GIAMBI .377 96 LANCE JOHNSON 198 94 JEFF BAGWELL 66 04 CARL CRAWFORD 23 00 DARIN ERSTAD .376 06 ICHIRO SUZUKI 196 94 LARRY WALKER 65 85 WILLIE WILSON 22 54 DON MUELLER .376 58 RICHIE ASHBURN 193 99 ROBIN VENTURA 65 06 GRADY SIZEMORE 22 97 LARRY -

Baseball Classics All-Time All-Star Greats Game Team Roster
BASEBALL CLASSICS® ALL-TIME ALL-STAR GREATS GAME TEAM ROSTER Baseball Classics has carefully analyzed and selected the top 400 Major League Baseball players voted to the All-Star team since it's inception in 1933. Incredibly, a total of 20 Cy Young or MVP winners were not voted to the All-Star team, but Baseball Classics included them in this amazing set for you to play. This rare collection of hand-selected superstars player cards are from the finest All-Star season to battle head-to-head across eras featuring 249 position players and 151 pitchers spanning 1933 to 2018! Enjoy endless hours of next generation MLB board game play managing these legendary ballplayers with color-coded player ratings based on years of time-tested algorithms to ensure they perform as they did in their careers. Enjoy Fast, Easy, & Statistically Accurate Baseball Classics next generation game play! Top 400 MLB All-Time All-Star Greats 1933 to present! Season/Team Player Season/Team Player Season/Team Player Season/Team Player 1933 Cincinnati Reds Chick Hafey 1942 St. Louis Cardinals Mort Cooper 1957 Milwaukee Braves Warren Spahn 1969 New York Mets Cleon Jones 1933 New York Giants Carl Hubbell 1942 St. Louis Cardinals Enos Slaughter 1957 Washington Senators Roy Sievers 1969 Oakland Athletics Reggie Jackson 1933 New York Yankees Babe Ruth 1943 New York Yankees Spud Chandler 1958 Boston Red Sox Jackie Jensen 1969 Pittsburgh Pirates Matty Alou 1933 New York Yankees Tony Lazzeri 1944 Boston Red Sox Bobby Doerr 1958 Chicago Cubs Ernie Banks 1969 San Francisco Giants Willie McCovey 1933 Philadelphia Athletics Jimmie Foxx 1944 St. -

2016 Topps Opening Day Baseball Checklist
BASE OD-1 Mike Trout Angels® OD-2 Noah Syndergaard New York Mets® OD-3 Carlos Santana Cleveland Indians® OD-4 Derek Norris San Diego Padres™ OD-5 Kenley Jansen Los Angeles Dodgers® OD-6 Luke Jackson Texas Rangers® Rookie OD-7 Brian Johnson Boston Red Sox® Rookie OD-8 Russell Martin Toronto Blue Jays® OD-9 Rick Porcello Boston Red Sox® OD-10 Felix Hernandez Seattle Mariners™ OD-11 Danny Salazar Cleveland Indians® OD-12 Dellin Betances New York Yankees® OD-13 Rob Refsnyder New York Yankees® Rookie OD-14 James Shields San Diego Padres™ OD-15 Brandon Crawford San Francisco Giants® OD-16 Tom Murphy Colorado Rockies™ Rookie OD-17 Kris Bryant Chicago Cubs® OD-18 Richie Shaffer Tampa Bay Rays™ Rookie OD-19 Brandon Belt San Francisco Giants® OD-20 Anthony Rizzo Chicago Cubs® OD-21 Mike Moustakas Kansas City Royals® OD-22 Roberto Osuna Toronto Blue Jays® OD-23 Jimmy Nelson Milwaukee Brewers™ OD-24 Luis Severino New York Yankees® Rookie OD-25 Justin Verlander Detroit Tigers® OD-26 Ryan Braun Milwaukee Brewers™ OD-27 Chris Tillman Baltimore Orioles® OD-28 Alex Rodriguez New York Yankees® OD-29 Ichiro Miami Marlins® OD-30 R.A. Dickey Toronto Blue Jays® OD-31 Alex Gordon Kansas City Royals® OD-32 Raul Mondesi Kansas City Royals® Rookie OD-33 Josh Reddick Oakland Athletics™ OD-34 Wilson Ramos Washington Nationals® OD-35 Julio Teheran Atlanta Braves™ OD-36 Colin Rea San Diego Padres™ Rookie OD-37 Stephen Vogt Oakland Athletics™ OD-38 Jon Gray Colorado Rockies™ Rookie OD-39 DJ LeMahieu Colorado Rockies™ OD-40 Michael Taylor Washington Nationals® OD-41 Ketel Marte Seattle Mariners™ Rookie OD-42 Albert Pujols Angels® OD-43 Max Kepler Minnesota Twins® Rookie OD-44 Lorenzo Cain Kansas City Royals® OD-45 Carlos Beltran New York Yankees® OD-46 Carl Edwards Jr. -
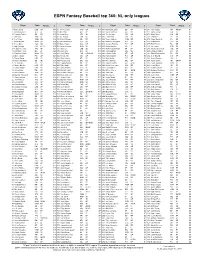
NL-Only Leagues
ESPN Fantasy Baseball top 360: NL-only leagues Player Team All pos. $ Player Team All pos. $ Player Team All pos. $ Player Team All pos. $ 1. Mookie Betts LAD OF $44 91. Joc Pederson CHC OF $14 181. MacKenzie Gore SD SP $7 271. John Curtiss MIA RP/SP $1 2. Ronald Acuna Jr. ATL OF $39 92. Will Smith ATL RP $14 182. Stefan Crichton ARI RP $6 272. Josh Fuentes COL 1B $1 3. Fernando Tatis Jr. SD SS $37 93. Austin Riley ATL 3B $14 183. Tim Locastro ARI OF $6 273. Wade Miley CIN SP $1 4. Juan Soto WSH OF $36 94. A.J. Pollock LAD OF $14 184. Lucas Sims CIN RP $6 274. Chad Kuhl PIT SP $1 5. Trea Turner WSH SS $32 95. Devin Williams MIL RP $13 185. Tanner Rainey WSH RP $6 275. Anibal Sanchez FA SP $1 6. Jacob deGrom NYM SP $30 96. German Marquez COL SP $13 186. Madison Bumgarner ARI SP $6 276. Rowan Wick CHC RP $1 7. Trevor Story COL SS $30 97. Raimel Tapia COL OF $13 187. Gregory Polanco PIT OF $6 277. Rick Porcello FA SP $0 8. Cody Bellinger LAD OF/1B $30 98. Carlos Carrasco NYM SP $13 188. Omar Narvaez MIL C $6 278. Jon Lester WSH SP $0 9. Freddie Freeman ATL 1B $29 99. Gavin Lux LAD 2B $13 189. Anthony DeSclafani SF SP $6 279. Antonio Senzatela COL SP $0 10. Christian Yelich MIL OF $29 100. Zach Eflin PHI SP $13 190. Josh Lindblom MIL SP $6 280. -

A Summer Wildfire: How the Greatest Debut in Baseball History Peaked and Dwindled Over the Course of Three Months
The Report committee for Colin Thomas Reynolds Certifies that this is the approved version of the following report: A Summer Wildfire: How the greatest debut in baseball history peaked and dwindled over the course of three months APPROVED BY SUPERVISING COMMITTEE: Co-Supervisor: ______________________________________ Tracy Dahlby Co-Supervisor: ______________________________________ Bill Minutaglio ______________________________________ Dave Sheinin A Summer Wildfire: How the greatest debut in baseball history peaked and dwindled over the course of three months by Colin Thomas Reynolds, B.A. Report Presented to the Faculty of the Graduate School of the University of Texas at Austin in Partial Fulfillment of the Requirements for the Degree of Master of Arts The University of Texas at Austin May, 2011 To my parents, Lyn & Terry, without whom, none of this would be possible. Thank you. A Summer Wildfire: How the greatest debut in baseball history peaked and dwindled over the course of three months by Colin Thomas Reynolds, M.A. The University of Texas at Austin, 2011 SUPERVISORS: Tracy Dahlby & Bill Minutaglio The narrative itself is an ageless one, a fundamental Shakespearean tragedy in its progression. A young man is deemed invaluable and exalted by the public. The hero is cast into the spotlight and bestowed with insurmountable expectations. But the acclamations and pressures are burdensome and the invented savior fails to fulfill the prospects once imagined by the public. He is cast aside, disregarded as a symbol of failure or one deserving of pity. It’s the quintessential tragedy of a fallen hero. The protagonist of this report is Washington Nationals pitcher Stephen Strasburg, who enjoyed a phenomenal rookie season before it ended abruptly due to a severe elbow injury. -
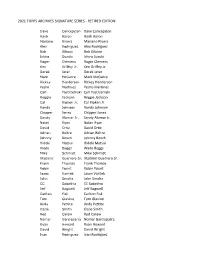
2021 Topps Archives Signature Series
2021 TOPPS ARCHVIES SIGNATURE SERIES - RETIRED EDITION Dave Concepcion Dave Concepcion Hank Aaron Hank Aaron Mariano Rivera Mariano Rivera Alex Rodriguez Alex Rodriguez Bob Gibson Bob Gibson Ichiro Suzuki Ichiro Suzuki Roger Clemens Roger Clemens Ken Griffey Jr. Ken Griffey Jr. Derek Jeter Derek Jeter Mark McGwire Mark McGwire Rickey Henderson Rickey Henderson Pedro Martinez Pedro Martinez Carl Yastrzemski Carl Yastrzemski Reggie Jackson Reggie Jackson Cal Ripken Jr. Cal Ripken Jr. Randy Johnson Randy Johnson Chipper Jones Chipper Jones Sandy Alomar Jr. Sandy Alomar Jr. Nolan Ryan Nolan Ryan David Ortiz David Ortiz Adrian Beltre Adrian Beltre Johnny Bench Johnny Bench Hideki Matsui Hideki Matsui Wade Boggs Wade Boggs Mike Schmidt Mike Schmidt Vladimir Guerrero Sr. Vladimir Guerrero Sr. Frank Thomas Frank Thomas Robin Yount Robin Yount Jason Varitek Jason Varitek John Smoltz John Smoltz CC Sabathia CC Sabathia Jeff Bagwell Jeff Bagwell Carlton Fisk Carlton Fisk Tom Glavine Tom Glavine Andy Pettite Andy Pettite Ozzie Smith Ozzie Smith Rod Carew Rod Carew Nomar Garciaparra Nomar Garciaparra Ryan Howard Ryan Howard David Wright David Wright Ivan Rodriguez Ivan Rodriguez Mike Mussina Mike Mussina Paul Molitor Paul Molitor Bernie Williams Bernie Williams Maury Wills Maury Wills Edgar Martinez Edgar Martinez Larry Walker Larry Walker Dale Murphy Dale Murphy Dave Parker Dave Parker Jorge Posada Jorge Posada Andre Dawson Andre Dawson Joe Mauer Joe Mauer Daryl Strawberry Daryl Strawberry Todd Helton Todd Helton Tim Lincecum Tim Lincecum Johnny Damon -

1 the Episcopal Church of the Good Shepherd the Rev. Morgan S
The Episcopal Church of the Good Shepherd The Rev. Morgan S. Allen March 18, 2018 V Lent, John 12:20-33 Come Holy Spirit, and enkindle in the hearts of your faithful, the fire of your Love. Amen. As the story goes, Mike Sweeney – a five-time Major League Baseball All-Star and just a couple of years older than I am – was walking through Central Park with his wife. As they strolled on this rare day off during the grind of a season, they approached a sandlot field and old backstop, where they could see in the distance a “guy playing long-toss [a stretching exercise]. [Sweeney] did the quick math and figured the stranger was throwing 300 feet on the fly[, that’s roughly the distance from an outfield foul pole to home plate, a rare achievement for a layman.] Curious, he [and his wife] walked closer. [As they approached the field, t]he guy [started to hit] balls into the backstop, [with] the powerful shotgun blast of real contact[, a sound] familiar to any serious ballplayer. [More] impressed[ now, Sweeney] got even closer, close enough to see. [He and his wife were surprised – and not so surprised – to realize that t]he man working out alone in Central Park was Ichiro [Suzuki, Sweeney’s teammate with the Seattle Mariners].”i Suzuki arrived to the United States to play baseball in 2001 when he was twenty-seven- years-old, having already collected 1,278 hits across nine seasons with the Orix Buffaloes of the Japanese professional league. In his rookie MLB season, Suzuki batted .350, stole 56 bases, and won both the Rookie of the Year and MVP awards, only the second player to win both honors in the same season [Quiz the congregation: Does anybody know the first player?]ii. -
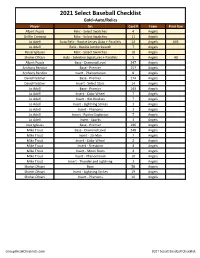
2021 Panini Select Baseball Checklist
2021 Select Baseball Checklist Gold=Auto/Relics Player Set Card # Team Print Run Albert Pujols Relic - Select Swatches 4 Angels Griffin Canning Relic - Select Swatches 11 Angels Jo Adell Auto Relic - Rookie Jersey Auto + Parallels 14 Angels 645 Jo Adell Relic - Rookie Jumbo Swatch 7 Angels Raisel Iglesias Relic - Select Swatches 18 Angels Shohei Ohtani Auto - Selective Signatures + Parallels 5 Angels 40 Albert Pujols Base - Diamond Level 247 Angels Anthony Rendon Base - Premier 157 Angels Anthony Rendon Insert - Phenomenon 8 Angels David Fletcher Base - Premier 174 Angels David Fletcher Insert - Select Stars 14 Angels Jo Adell Base - Premier 143 Angels Jo Adell Insert - Color Wheel 7 Angels Jo Adell Insert - Hot Rookies 7 Angels Jo Adell Insert - Lightning Strikes 1 Angels Jo Adell Insert - Phenoms 3 Angels Jo Adell Insert - Rookie Explosion 7 Angels Jo Adell Insert - Sparks 1 Angels Jose Iglesias Base - Premier 196 Angels Mike Trout Base - Diamond Level 248 Angels Mike Trout Insert - 25-Man 7 Angels Mike Trout Insert - Color Wheel 2 Angels Mike Trout Insert - Firestorm 4 Angels Mike Trout Insert - Moon Shots 4 Angels Mike Trout Insert - Phenomenon 10 Angels Mike Trout Insert - Thunder and Lightning 3 Angels Shohei Ohtani Base 58 Angels Shohei Ohtani Insert - Lightning Strikes 19 Angels Shohei Ohtani Insert - Phenoms 10 Angels GroupBreakChecklists.com 2021 Select Baseball Checklist Player Set Card # Team Print Run Abraham Toro Relic - Select Swatches 1 Astros Alex Bregman Auto - Moon Shot Signatures + Parallels 2 Astros 102 Bryan Abreu -

List of Players in Apba's 2018 Base Baseball Card
Sheet1 LIST OF PLAYERS IN APBA'S 2018 BASE BASEBALL CARD SET ARIZONA ATLANTA CHICAGO CUBS CINCINNATI David Peralta Ronald Acuna Ben Zobrist Scott Schebler Eduardo Escobar Ozzie Albies Javier Baez Jose Peraza Jarrod Dyson Freddie Freeman Kris Bryant Joey Votto Paul Goldschmidt Nick Markakis Anthony Rizzo Scooter Gennett A.J. Pollock Kurt Suzuki Willson Contreras Eugenio Suarez Jake Lamb Tyler Flowers Kyle Schwarber Jesse Winker Steven Souza Ender Inciarte Ian Happ Phillip Ervin Jon Jay Johan Camargo Addison Russell Tucker Barnhart Chris Owings Charlie Culberson Daniel Murphy Billy Hamilton Ketel Marte Dansby Swanson Albert Almora Curt Casali Nick Ahmed Rene Rivera Jason Heyward Alex Blandino Alex Avila Lucas Duda Victor Caratini Brandon Dixon John Ryan Murphy Ryan Flaherty David Bote Dilson Herrera Jeff Mathis Adam Duvall Tommy La Stella Mason Williams Daniel Descalso Preston Tucker Kyle Hendricks Luis Castillo Zack Greinke Michael Foltynewicz Cole Hamels Matt Harvey Patrick Corbin Kevin Gausman Jon Lester Sal Romano Zack Godley Julio Teheran Jose Quintana Tyler Mahle Robbie Ray Sean Newcomb Tyler Chatwood Anthony DeSclafani Clay Buchholz Anibal Sanchez Mike Montgomery Homer Bailey Matt Koch Brandon McCarthy Jaime Garcia Jared Hughes Brad Ziegler Daniel Winkler Steve Cishek Raisel Iglesias Andrew Chafin Brad Brach Justin Wilson Amir Garrett Archie Bradley A.J. Minter Brandon Kintzler Wandy Peralta Yoshihisa Hirano Sam Freeman Jesse Chavez David Hernandez Jake Diekman Jesse Biddle Pedro Strop Michael Lorenzen Brad Boxberger Shane Carle Jorge de la Rosa Austin Brice T.J. McFarland Jonny Venters Carl Edwards Jackson Stephens Fernando Salas Arodys Vizcaino Brian Duensing Matt Wisler Matt Andriese Peter Moylan Brandon Morrow Cody Reed Page 1 Sheet1 COLORADO LOS ANGELES MIAMI MILWAUKEE Charlie Blackmon Chris Taylor Derek Dietrich Lorenzo Cain D.J. -

Tonight's Game Information
Thursday, April 1, 2021 Game #1 (0-0) T-Mobile Park SEATTLE MARINERS (0-0) vs. SAN FRANCISCO GIANTS (0-0) Home #1 (0-0) TONIGHT’S GAME INFORMATION Starting Pitchers: LHP Marco Gonzales (7-2, 3.10 in ‘20) vs. RHP Kevin Gausman (3-3, 3.62 in ‘20) 7:10 pm PT • Radio: 710 ESPN / Mariners.com • TV: ROOT SPORTS NW Day Date Opp. Time (PT) Mariners Pitcher Opposing Pitcher RADIO Friday April 2 vs. SF 7:10 pm LH Yusei Kikuchi (6-9, 5.12 in ‘20) vs. RH Johnny Cueto (2-3, 5.40 in ‘20) 710 ESPN Saturday April 3 vs. SF 6:10 pm RH Chris Flexen (8-4, 3.01 in ‘20 KBO) vs. RH Logan Webb (3-4, 5.47 in ‘20) 710 ESPN Sunday April 4 OFF DAY TONIGHT’S TILT…the Mariners open their 45th season against the San Francisco Giants at T-Mobile INSIDE THE NUMBERS Park…tonight is the first of a 3-game series vs. the Giants…following Saturday’s game, the Mariners will enjoy an off day before hosting the White Sox for a 3-game set beginning on Monday, April 5…tonight’s game will be televised live on ROOT SPORTS NW and broadcast live on 710 ESPN Seattle and the 2 Mariners Radio Network. With a win in tonight’s game, Marco Gonzales would join Randy Johnson ODDS AND ENDS…the Mariners open the season against San Francisco for the first time in club history with 2 wins on Opening Day, trailing ...also marks the first time in club history the Mariners open with an interleague opponent...the Mariners are only Félix Hernández (7) for the most 12-4 over their last 16 Opening Day contests...are 3-1 at home during that span. -

Uehara Gives up Walk and Win to Padres
Sports FRIDAY, JUNE 23, 2017 42 Uehara gives up walk and win to Padres CHICAGO: Chicago’s Japanese reliever Koji Uehara gave up an eighth-inning walk with bases loaded to help San Diego to a come-from-behind 3-2 win over the Cubs in Major League Baseball on Wednesday. After the Padres’ Erick Aybar hit a tying home run in the sixth inning, Luis Torrens walked with the bases loaded against Uehara, and San Diego stopped a three-game losing streak. Chicago rookie Ian Happ hit a two- run homer in the fourth against reliever Craig Stammen, going deep for the second straight game and third time in four. Uehara (2-4), the fifth of six Cubs relievers, replaced Pedro Strop starting the eighth and allowed singles to Wil Myers leading off and Cory Spangenberg with one out. Aybar was intentionally walked, loading the bases, Matt Szczur fouled out and Torrens took a 3-1 fastball that sailed inside. Phil Maton (1-0), the third of five Padres relievers, pitched a score- less seventh for his first major league win, and Brandon Maurer got two outs for his 13th save. MARLINS 2, NATIONALS 1 Max Scherzer’s bid for the third no-hitter of his big league career ended with one out in the eighth inning, and he then gave up two unearned runs as the Miami Marlins rallied to beat the Washington Nationals 2-1. After backup catcher AJ Ellis reached on an infield single for Miami’s first hit, an error by first baseman Adam Lind and a hit batter loaded the bases with two outs.