PETAL: Preset Encoding Table Information Leakage
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Table Lens: Merging Graphical and Symbolic Representations in an Interactive Focus+ Context Visualization for Tabular Information
HumanFac(orsinComputingSystems CHI’94 0 “Celebra/i//ghrferdepende)~cc” The Table Lens: Merging Graphical and Symbolic Representations in an Interactive Focus+ Context Visualization for Tabular Information Ramana Rao and Stuart K. Card Xerox Palo Alto Research Center 3333 Coyote Hill Road Palo Alto, CA 94304 Gao,carcM@parc. xerox.com ABSTRACT (at cell size of 100 by 15 pixels, 82dpi). The Table Lens can We present a new visualization, called the Table Lens, for comfortably manage about 30 times as many cells and can visualizing and making sense of large tables. The visual- display up to 100 times as many cells in support of many ization uses a focus+ccmtext (fisheye) technique that works tasks. The scale advantage is obtained by using a so-called effectively on tabular information because it allows display “focus+context” or “fisheye” technique. These techniques of crucial label information and multiple distal focal areas. allow interaction with large information structures by dynam- In addition, a graphical mapping scheme for depicting table ically distorting the spatial layout of the structure according to contents has been developed for the most widespread kind the varying interest levels of its parts. The design of the Table of tables, the cases-by-variables table. The Table Lens fuses Lens technique has been guided by the particular properties symbolic and gaphical representations into a single coherent and uses of tables. view that can be fluidly adjusted by the user. This fusion and A second contribution of our work is the merging of graphical interactivity enables an extremely rich and natural style of representations directly into the process of table visualization direct manipulation exploratory data analysis. -

Army Acquisition Workforce Dependency on E-Mail for Formal
ARMY ACQUISITION WORKFORCE DEPENDENCY ON E-MAIL FOR FORMAL WORK COORDINATION: FINDINGS AND OPPORTUNITIES FOR WORKFORCE PERFORMANCE IMPROVEMENT THROUGH E-MAIL-BASED SOCIAL NETWORK ANALYSIS KENNETH A. LORENTZEN May 2013 PUBLISHED BY THE DEFENSE ACQUISITION UNIVERSITY PRESS PROJECT ADVISOR: BOB SKERTIC CAPITAL AND NORTHEAST REGION, DAU THE SENIOR SERVICE COLLEGE FELLOWSHIP PROGRAM ABERDEEN PROVING GROUND, MD PAGE LEFT BLANK INTENTIONALLY .ARMY ACQUISITION WORKFORCE DEPENDENCY ON E-MAIL FOR FORMAL WORK COORDINATION: FINDINGS AND OPPORTUNITIES FOR WORKFORCE PERFORMANCE IMPROVEMENT THROUGH E-MAIL-BASED SOCIAL NETWORK ANALYSIS KENNETH A. LORENTZEN May 2013 PUBLISHED BY THE DEFENSE ACQUISITION UNIVERSITY PRESS PROJECT ADVISOR: BOB SKERTIC CAPITAL AND NORTHEAST REGION, DAU THE SENIOR SERVICE COLLEGE FELLOWSHIP PROGRAM ABERDEEN PROVING GROUND, MD PAGE LEFT BLANK INTENTIONALLY ii Table of Contents Table of Contents ............................................................................................................................ ii List of Figures ................................................................................................................................ vi Abstract ......................................................................................................................................... vii Chapter 1—Introduction ................................................................................................................. 1 Background and Motivation ................................................................................................. -

Geotime As an Adjunct Analysis Tool for Social Media Threat Analysis and Investigations for the Boston Police Department Offeror: Uncharted Software Inc
GeoTime as an Adjunct Analysis Tool for Social Media Threat Analysis and Investigations for the Boston Police Department Offeror: Uncharted Software Inc. 2 Berkeley St, Suite 600 Toronto ON M5A 4J5 Canada Business Type: Canadian Small Business Jurisdiction: Federally incorporated in Canada Date of Incorporation: October 8, 2001 Federal Tax Identification Number: 98-0691013 ATTN: Jenny Prosser, Contract Manager, [email protected] Subject: Acquiring Technology and Services of Social Media Threats for the Boston Police Department Uncharted Software Inc. (formerly Oculus Info Inc.) respectfully submits the following response to the Technology and Services of Social Media Threats RFP. Uncharted accepts all conditions and requirements contained in the RFP. Uncharted designs, develops and deploys innovative visual analytics systems and products for analysis and decision-making in complex information environments. Please direct any questions about this response to our point of contact for this response, Adeel Khamisa at 416-203-3003 x250 or [email protected]. Sincerely, Adeel Khamisa Law Enforcement Industry Manager, GeoTime® Uncharted Software Inc. [email protected] 416-203-3003 x250 416-708-6677 Company Proprietary Notice: This proposal includes data that shall not be disclosed outside the Government and shall not be duplicated, used, or disclosed – in whole or in part – for any purpose other than to evaluate this proposal. If, however, a contract is awarded to this offeror as a result of – or in connection with – the submission of this data, the Government shall have the right to duplicate, use, or disclose the data to the extent provided in the resulting contract. GeoTime as an Adjunct Analysis Tool for Social Media Threat Analysis and Investigations 1. -

Inviwo — a Visualization System with Usage Abstraction Levels
IEEE TRANSACTIONS ON VISUALIZATION AND COMPUTER GRAPHICS, VOL X, NO. Y, MAY 2019 1 Inviwo — A Visualization System with Usage Abstraction Levels Daniel Jonsson,¨ Peter Steneteg, Erik Sunden,´ Rickard Englund, Sathish Kottravel, Martin Falk, Member, IEEE, Anders Ynnerman, Ingrid Hotz, and Timo Ropinski Member, IEEE, Abstract—The complexity of today’s visualization applications demands specific visualization systems tailored for the development of these applications. Frequently, such systems utilize levels of abstraction to improve the application development process, for instance by providing a data flow network editor. Unfortunately, these abstractions result in several issues, which need to be circumvented through an abstraction-centered system design. Often, a high level of abstraction hides low level details, which makes it difficult to directly access the underlying computing platform, which would be important to achieve an optimal performance. Therefore, we propose a layer structure developed for modern and sustainable visualization systems allowing developers to interact with all contained abstraction levels. We refer to this interaction capabilities as usage abstraction levels, since we target application developers with various levels of experience. We formulate the requirements for such a system, derive the desired architecture, and present how the concepts have been exemplary realized within the Inviwo visualization system. Furthermore, we address several specific challenges that arise during the realization of such a layered architecture, such as communication between different computing platforms, performance centered encapsulation, as well as layer-independent development by supporting cross layer documentation and debugging capabilities. Index Terms—Visualization systems, data visualization, visual analytics, data analysis, computer graphics, image processing. F 1 INTRODUCTION The field of visualization is maturing, and a shift can be employing different layers of abstraction. -
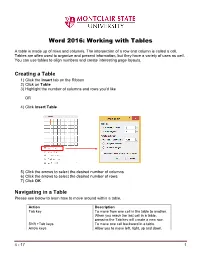
Word 2016: Working with Tables
Word 2016: Working with Tables A table is made up of rows and columns. The intersection of a row and column is called a cell. Tables are often used to organize and present information, but they have a variety of uses as well. You can use tables to align numbers and create interesting page layouts. Creating a Table 1) Click the Insert tab on the Ribbon 2) Click on Table 3) Highlight the number of columns and rows you’d like OR 4) Click Insert Table 5) Click the arrows to select the desired number of columns 6) Click the arrows to select the desired number of rows 7) Click OK Navigating in a Table Please see below to learn how to move around within a table. Action Description Tab key To move from one cell in the table to another. When you reach the last cell in a table, pressing the Tab key will create a new row. Shift +Tab keys To move one cell backward in a table. Arrow keys Allow you to move left, right, up and down. 4 - 17 1 Selecting All or Part of a Table There are times you want to select a single cell, an entire row or column, multiple rows or columns, or an entire table. Selecting an Individual Cell To select an individual cell, move the mouse to the left side of the cell until you see it turn into a black arrow that points up and to the right. Click in the cell at that point to select it. Selecting Rows and Columns To select a row in a table, move the cursor to the left of the row until it turns into a white arrow pointing up and to the right, as shown below. -

Table Understanding Through Representation Learning
TURL: Table Understanding through Representation Learning Xiang Deng∗ Huan Sun∗ Alyssa Lees The Ohio State University The Ohio State University Google Research Columbus, Ohio Columbus, Ohio New York, NY [email protected] [email protected] [email protected] You Wu Cong Yu Google Research Google Research New York, NY New York, NY [email protected] [email protected] ABSTRACT Relational tables on the Web store a vast amount of knowledge. Owing to the wealth of such tables, there has been tremendous progress on a variety of tasks in the area of table understanding. However, existing work generally relies on heavily-engineered task- specific features and model architectures. In this paper, we present TURL, a novel framework that introduces the pre-training/fine- tuning paradigm to relational Web tables. During pre-training, our framework learns deep contextualized representations on relational tables in an unsupervised manner. Its universal model design with pre-trained representations can be applied to a wide range of tasks with minimal task-specific fine-tuning. Specifically, we propose a structure-aware Transformer encoder to model the row-column structure of relational tables, and present a new Masked Entity Recovery (MER) objective for pre-training to capture the semantics and knowledge in large-scale unlabeled data. Figure 1: An example of a relational table from Wikipedia. We systematically evaluate TURL with a benchmark consisting of 6 different tasks for table understanding (e.g., relation extraction, a total of 14.1 billion tables in 2008. More recently, Bhagavatula et al. cell filling). We show that TURL generalizes well to all tasks and [4] extracted 1.6M high-quality relational tables from Wikipedia. -

VTK File Formats
File Formats for VTK Version 4.2 (Taken from The VTK User’s Guide Contact Kitware www.kitware.com to purchase) VTK File Formats The Visualization Toolkit provides a number of source and writer objects to read and write popular data file formats. The Visualization Toolkit also provides some of its own file formats. The main reason for creating yet another data file format is to offer a consistent data representation scheme for a variety of dataset types, and to provide a simple method to com- municate data between software. Whenever possible, we recommend that you use formats that are more widely used. But if this is not possible, the Visualization Toolkit formats described here can be used instead. Note that these formats may not be supported by many other tools. There are two different styles of file formats available in VTK. The simplest are the legacy, serial formats that are easy to read and write either by hand or programmatically. However, these formats are less flexible than the XML based file formats described later in this section. The XML formats support random access, parallel I/O, and portable data com- pression and are preferred to the serial VTK file formats whenever possible. Simple Legacy Formats The legacy VTK file formats consist of five basic parts. 1. The first part is the file version and identifier. This part contains the single line: # vtk DataFile Version x.x. This line must be exactly as shown with the exception of the version number x.x, which will vary with different releases of VTK. -

000 Computer Science, Information, General Works
000 000 Computer science, information, general works SUMMARY 001–006 [Knowledge, the book, systems, computer science] 010 Bibliography 020 Library and information sciences 030 General encyclopedic works 050 General serial publications 060 General organizations and museology 070 Documentary media, educational media, news media; journalism; publishing 080 General collections 090 Manuscripts, rare books, other rare printed materials 001 Knowledge Description and critical appraisal of intellectual activity in general Including interdisciplinary works on consultants Class here discussion of ideas from many fields; interdisciplinary approach to knowledge Class epistemology in 121. Class a compilation of knowledge in a specific form with the form, e.g., encyclopedias 030 For consultants or use of consultants in a specific subject, see the subject, e.g., library consultants 023, engineering consultants 620, use of consultants in management 658.4 See Manual at 500 vs. 001 .01 Theory of knowledge Do not use for philosophy of knowledge, philosophical works on theory of knowledge; class in 121 .1 Intellectual life Nature and value For scholarship and learning, see 001.2 See also 900 for broad description of intellectual situation and condition 217 001 Dewey Decimal Classification 001 .2 Scholarship and learning Intellectual activity directed toward increase of knowledge Class methods of study and teaching in 371.3. Class a specific branch of scholarship and learning with the branch, e.g., scholarship in the humanities 001.3, in history 900 For research, -

Geotime Product Evaluation Lex Berman, CGA 12 Dec 09 Abstract
GeoTime Product Evaluation Lex Berman, CGA 12 Dec 09 Abstract: GeoTime is a stand-alone spatio-temporal browser with built-in queries for analyzing imported datasets containing events with defined spatial and temporal footprints. Events can be viewed as discrete points in a 3D space- time cube (with the the z-value representing the time axis), or can be viewed as entities (which are comprised of multiple location-events). The current version of GeoTime can directly load tables and flat files (including KML), but must be used together with ESRI ArcGIS to load from shapefiles and layers. Installation : The installation package for GeoTime includes an executable installer (for Windows only), a license file, and a third-party map library application, called MapMan. For GeoTime to run with ESRI files, both ArcGIS 9.2 or 9.3 must be installed, along with .NET, and Excel. Installation on ArcGIS 9.3 worked as expected during testing, but failed to completely integrate with ArcGIS 9.2 (due to an error with ESRI .NET assemblies). On the ArcGIS 9.3 install, the application worked for the administrator user profile only. It was not clear how to install the application for all user profiles. There are some options for installing the application with a license server, presumably to run as a keyed application over a limited subnet group of machines. However, since we are using the trial-period stand-alone client we don't know the level of difficulty in getting the license server (third-party software) to run. The MapMan package, included with GeoTime, takes considerably longer than GeoTime to install. -

Department of Pathology and Laboratory Medicine 2012-2013 Annual Report
DEPARTMENT OF PATHOLOGY AND LABORATORY MEDICINE 2012-2013 ANNUAL REPORT TABLE OF CONTENTS Faculty Roster . 1 Research and Scholarly Accomplishments . 8 Teaching . 38 Medical Teaching . 38 Dental Teaching . 39 Molecular and Cellular Pathology Graduate Program . 40 Residency Training Program . 42 Subspecialty Fellowship Training Program . 43 Clinical Chemistry Fellowship . 43 Clinical Microbiology Fellowship . 44 Clinical Molecular Genetics Fellowship . 44 Clinical Molecular Pathology Fellowship. 45 Coagulation Fellowship. 45 Cytogenetics Fellowship. 45 Cytopathology Fellowship. 46 Forensic Pathology Fellowship. 46 Hematopathology Fellowship. 47 Nephropathology Fellowship. 47 Surgical Pathology Fellowship. 48 Transfusion Medicine Fellowship. 48 Grand Rounds Seminars . 48 Clinical Services . 53 Background. 53 McLendon Clinical Laboratories Herbert Whinna, M.D. Ph.D., Director Surgical Pathology (Histology/Special Procedures) . 53 William K. Funkhouser, M.D., Ph.D., Director Cytopathology . 54 Susan J. Maygarden, M.D., Director Autopsy Pathology. 54 Leigh B. Thorne, M.D., Director Molecular Pathology. 55 Margaret L. Gulley, M.D., Director i Transfusion Medicine, Apheresis, Transplant Services. 56 Yara A. Park, M.D., Director Clinical Microbiology, Immunology. 56 Peter H. Gilligan, Ph.D., Director Phlebotomy. 59 Peter H. Gilligan, Ph.D., Director Core Laboratory (Chem./UA/Coag./Hem/Tox/Endo) . 59 Catherine A. Hammett-Stabler, Ph.D., Director Hematopathology . 60 George Fedoriw, M.D., Director Special Coagulation . 60 Herbert C. Whinna, M.D., Ph.D., Director Cytogenetics . 61 Kathleen W. Rao, Ph.D., Director Kathleen A. Kaiser-Rogers, Co-Director Laboratory Information Services . 62 Herbert C. Whinna, M.D., Ph.D., Director Nephropathology Laboratory. 62 Volker R. Nickeleit, M.D., Director Quality Management . 63 Herbert C. Whinna, M.D., Ph.D., Director Neuropathology . -

Emo Onally Looking Eyes
Emo$onally Looking Eyes 2012 Winter vacaon internship Gahye Park Introduc$on • Overview – Review – Goal • Progress summary • Progress – Weekly progress & Difficules • Conclusion Overview - Review • Volume Rendering – Rendering data set like a group of 2D slice images ac quired by a CT, MRI, or MicroCT scanner • Volume ray cas$ng – Ray cas$ng, Sampling, Shading, Composing Overview - Review • Exis$ng eyeball rendering – Eyeball • Ar$ficial 3D model – Iris • Paste texture • Overlapped semi-transparent layers – Ar$ficial data – Lack of depth informaon Overview - Goal • Rendering emo$onally looking eyes – Real anatomical data – Include human $ssue informaon → Natural liveliness Progress Summary • Find eyeball or similar 3rd • Learn voreen (video, programming tutorials) • Render data similar to eyeball by • Find volume data and render it by voreen week voreen(VOlume REndering ENgine) • Learn voreen(slides tutorial) th • Get scanned eyeball data 4 • Find dicom data for segmentaon • Extract and refine eyeball data week • Extract eyes and check this briefly using Seg3D and voreen • 30, 2/1 : hci 2013 5th • Refine and finish extrac:ng 2 ct results • Adjust OTF(Opacity Transfer Func$on) week table • Parcipate HCI conference 1st • Finish adJus:ng o table • Adjust OTF table and shader week • Learn volume rendering tutorial for shader coding 2nd • Adjust OTF table and shader week • vacaon • Lunar new year & Vacaon rd • vacaon 3 • Vacaon week • Analyze results and improvement 4th • Consider expected effect • Analyze exis:ng shader code week • Complete the project • Prepare progress the presentaon Progress (Jan. 3rd week) • Find volume data set – The Volume Library head data set Descripon Picture MRI Head 14M 256x256x256 MRI Woman 7.7M 256x256x109 CT Visible Male 2.8M 128x256x256 Progress (Jan. -

6-Michalek Et Al.Indd
The negotiation position amid member states of the EU Vyjednávací pozice mezi členskými státy P. MICHÁLEK, P. RYMEŠOVÁ, L. MÜLLEROVÁ, H. CHAMOUTOVÁ, K. CHAMOUTOVÁ Czech University of Agriculture, Prague, Czech Republic Abstract: The European integration process is very important and it has been paid attention to for the last 15 years. The abstract deals with the negotiation field and position in the structure of the current expanded EU. For better orientation in this equivocal situation, a modern cartography method of relationship in the arbitrary group called dynamic sociometry was used. The method is based on classical sociometry Morena and furthermore it uses the instrument of fuzzy set, typo- logy and structural analysis. The output of this method is a sociomap. The map holds information on the relative closeness or the distance of individual elements, their configuration but also some quality information. The graphic chart is similar to a topographic map. In our case, the sociomap was created from the data of foreign business among the member coun- tries. The following analysis of the sociomap we detected and described characteristic features of the analysed group. It consists of formal and informal links in the group, the role and the position of each member within the group, the structure and relations in the group. In the concrete, we attained data to answer the questions about the present climate in interre- lationships in the EU, which means the relationships among the members as the whole entities but also the relationships separately among members themselves. The position analysis of the Czech Republic in the system of the created sociomaps was considered as very important.