Thomas Pütterich Investigations on Spectroscopic Diagnostic
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Trex Measurements of Mineralogical Samples in the Psi Lab from the Vacuum-Uv to Thermal Infrared Wavelengths N.C
50th Lunar and Planetary Science Conference 2019 (LPI Contrib. No. 2132) 2842.pdf TREX MEASUREMENTS OF MINERALOGICAL SAMPLES IN THE PSI LAB FROM THE VACUUM-UV TO THERMAL INFRARED WAVELENGTHS N.C. Pearson1 R.N. Clark1, A.R. Hendrix1 and the TREX team. 1Plane- tary Science Institute, Tucson, AZ, 85719 USA , [email protected] Introduction: The Toolbox for Research and Ex- under vacuum. A single axis movable stage has been ploration (TREX) is a NASA SSERVI (Solar System installed that can be cooled using circulated liquid ni- Exploration Research Virtual Institute) node. TREX trogen, or heated with resistor. Two temperature (trex.psi.edu) aims to decrease risk to future missions, probes have been installed so that both ambient tem- specifically to the Moon, the Martian moons, and near- perature of the chamber, and the temperature of the Earth asteroids, by improving mission success and as- sample can be recorded, which when combined with suring the safety of astronauts, their instruments, and pressure sensor readings can used to estimate relative spacecraft. TREX studies will focus on characteristics humidity inside the chamber. Illumination of the sam- of the fine grains that cover the surfaces of these target ple comes from a vacuum-UV-visible spectrum deu- bodies – their spectral characteristics and the potential terium lamp, and a tungsten halogen lamp for the visi- resources (such as H2O) they may harbor. TREX stud- ble and near infrared. The deuterium lamp also acts to ies are organized into four Themes: lab studies [1], simulate the harsh UV exposure airless surfaces are ex- Moon studies [2], small-bodies studies [3], and field posed to in space. -

Solar-Terrestrial Centre of Excellence Activity Report 2009
STCE Activities Report 2009 Solar-Terrestrial Centre of Excellence Activity Report 2009 Table of Contents PART 1 ........................................................................................................................................... 4 A. Common Public Outreach and Science Communication .................................................. 4 A.1. Objectives .................................................................................................................................... 4 A.2. Progress and results ..................................................................................................................... 4 A.2.1. Internal communication ...................................................................................................... 4 A.2.2. Communication towards external entities ........................................................................... 5 A.2.3. The Sixth European Space Weather Week, ESWW6 ......................................................... 5 A.2.4. Salon du Bourget ................................................................................................................ 6 A.2.5. Open doors .......................................................................................................................... 7 A.2.6. PROBA2 ............................................................................................................................. 8 A.2.7. The Sun is NOT dead ....................................................................................................... -

1M F.L. Soft X-Ray and Extreme UV Monochromator
248/310 1m f.l. Soft X-ray and Extreme UV Monochromator The 248/310 is a 1000 mm focal length Rowland circle grazing incidence vacuum monochromator. It has 0.02 nm fwhm spectral resolution with 1200 g/mm grating. Its precision slits are micrometer adjustable from 0.005 to 0.5 mm. The 248/310 features a chord-length meter and manually operable wavelength drive for years of accurate and reproducible wavelength positioning. The scan controller provides computer/software control. The high performance instrument provides excellent performance from 1 nanometer up to 300 nm in the UV. Use the 248/310 for XUV, SXR or extreme UV applications. The compact housing is easily adapted to most experiments. We can provide it complete with vacuum pumps, microchannel plates and CCD detectors. 1 to 310nm range | Direct-CCD, scanning slit, MCP configurations | Large assortment of gratings Optical Design Rowland Circle Grazing Incidence Monochromator Angle of Incidence 87 degrees standard, 84 to 88 degrees optionally available Focal Length 1 meter Acceptance 20 mrad Wavelength Range refer to grating of interest for range Grating Size 20 x 25 mm (single, kinematic grating holder) Slits Continuously variable micrometer actuated width 0.01 to 0.5 mm. Settable height. Vacuum High vacuum 10E-6 torr standard, UHV optionally available Focal Plane 40 mm microchannel plate or 25 mm direct detection CCD Ordering Information Part Number: 181-104424 = Model 248/310 Rowland circle grazing incidence monochromator, 1m, 20 mrad, adjustable entrance and exit slits (requires -

4-Instruments for the Extreme Ultraviolet
4-instruments for the extreme ultraviolet Four instrument systems developed specifically for analytical and diagnostic spectral metrology of soft x-ray and ultrafast extreme ultraviolet photon sources and laser systems. These spectrometer instruments can make optical measurements from 0.5 to more than 500 nanometers. Working in the UV? McPherson has it covered. McPherson makes spectrometers proven to work at the shortest optical wavelengths. From wavelengths less than one nanometer, up to the visible light range, our analytical and diagnostic instruments fit to your application. They work in high harmonic generation (HHG) laser diagnostics. They work in advanced semiconductor extreme UV metrology and analytics. They work in high temperature soft x-ray plasma physics diagnostics. All are available for ultra high (UHV) or high-vacuum applications. McPherson manufactures numerous spectrometer models and optical designs. Here are those with staying power popular across many spectroscopy disciplines. 1. For measuring low energy deep-UV wavelengths (50-500nm) there is the Model 234/302. It’s a great instrument to transition from ultraviolet to wavelengths as short as 30 nanometers. Works equally well in scanning applications as with direct detection CCD for rapid collection of diagnostic spectra. If you need finer spectral resolution, consider Model 235 or Model 225 for the same wavelength range. 2. Do you need analysis and diagnostics with high energy spectra (1-300nm)? Then the vacuum ultraviolet (VUV) Model 248/310 fits the bill. It works with point detectors or as a scanning monochromator using concave spherical gratings. The slit or detectors scan along the Rowland circle. It works with direct- detection CCD, MCP intensifier, and when integrated with a spectral lamp, makes a tunable light source. -
VUV Spectrophotometer.Pdf
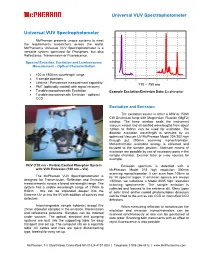
Universal VUV Spectrophotometer Universal VUV Spectrophotometer .00005 McPherson presents unique systems to meet the requirements researchers across the world. .00004 McPherson’s Universal VUV Spectrophotometer is a versatile system optimized for Phosphors, but also .00003 Reflectance, Transmission or Fluorescence. .00002 Spectral Emission, Excitation and Luminescence Measurement ~ Optical Characterization .00001 • 120 to 1800nm wavelength range 0 • 5 sample positions 100 200 300 400 500 600 700 • Lifetime / Persistence measurement capability 110 – 750 nm • PMT (optionally cooled) with signal recovery • Tunable monochromatic Excitation Example Excitation/Emission Data: Eu phosphor • Tunable monochromatic Emission - optional CCD Excitation and Emission The excitation source is either a 30W or 150W CW Deuterium lamp with Magnesium Fluoride (MgF2) window. The lamp window seals the instrument vacuum vessel and all emitted wavelengths from about 120nm to 380nm can be used for excitation. The discrete excitation wavelength is selected by an optimized Vacuum UV McPherson Model 234/302 high through put 200mm scanning monochromator. Monochromatic excitation energy is collected and focused to the sample position. Alternate means of excitation are possible by use of accessory ports in the sample chamber, Excimer laser or x-ray sources for example. VUV (120 nm - Visible) Excited Phosphor System Emission spectrum is detected with a with VUV Emission (120 nm – Vis) McPherson Model 218 high resolution 300mm scanning monochromator. It can scan from 105nm to The McPherson VUV Spectrophotometer is far IR spectral region. If emission spectra are always designed for Transmission, Reflection and Emission >200nm, we substitute a Model 2035 high resolution measurements across a broad wavelength range. The scanning spectrometer. The sample emission is system has a usable wavelength range of 115nm to collected and focused to the entrance slit. -

Illumination for Coherent Soft X-Ray Applications: the New X1A Beamline at the NSLS
395 J. Synchrotron Rad. (2000). 7, 395±404 Illumination for coherent soft X-ray applications: the new X1A beamline at the NSLS B. Winn,a H. Ade,b C. Buckley,c M. Feser,a M. Howells,d S. Hulbert,e C. Jacobsen,a K. Kaznacheyev,a J. Kirz,a* A. Osanna,a J. Maser,a² I. McNulty,f J. Miao,a³ T. Oversluizen,g S. Spector,a§ B. Sullivan,a} Yu. Wang,a²² S. Wiricka and H. Zhangb³³ aDepartment of Physics and Astronomy, SUNY at Stony Brook, Stony Brook, NY 11794-3800, USA, bDepartment of Physics, North Carolina State University, Raleigh, NC 27599, USA, cPhysics Department, King's College, London WC2R 2LS, UK, dAdvanced Light Source, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA, eNational Synchrotron Light Source, Brookhaven National Laboratory, Upton, NY 11973, USA, fAdvanced Photon Source, Argonne National Laboratory, Argonne, IL 60439, USA, and gCreative Instrumentation, 412 South Country Road, East Patchogue, NY 11772, USA. E-mail: [email protected] (Received 19 July 2000; accepted 19 September 2000) The X1A soft X-ray undulator beamline at the NSLS has been rebuilt to serve two microscopy stations operating simultaneously. Separate spherical-grating monochromators provide the resolving power required for XANES spectroscopy at the C, N and O absorption edges. The exit slits are ®xed and de®ne the coherent source for the experiments. The optical design and the operational performance are described. Keywords: beamlines; microscopy; coherence; soft X-rays; undulators. 1. Introduction Skrinsky (1977) pointed out that the coherent intensity obtained by collimation from an incoherent source is Coherence in the visible range of the electromagnetic directly proportional to the source brightness, and that spectrum is routinely obtained using lasers. -

Trex Uv-Vis Lab Measurements of Minerals and Mineral-Ice Mixtures
50th Lunar and Planetary Science Conference 2019 (LPI Contrib. No. 2132) 3088.pdf TREX UV-VIS LAB MEASUREMENTS OF MINERALS AND MINERAL-ICE MIXTURES. G. M. Holsclaw1 , M. M. Osterloo1, T. Munsat2, and A. R. Hendrix3, 1Laboratory for Atmospheric and Space Physics, Uni- versity of Colorado at Boulder, 1234 Innovation Dr, Boulder, CO 80303, USA ([email protected]), 2Department of Physics, University of Colorado, Boulder, Colorado 80309, USA, 3Planetary Science Institute, Tuc- son, AZ. Introduction: The Toolbox for Research and Ex- tionality (this or N2 purge necessary for measurements ploration (TREX) is a NASA SSERVI (Solar System < 200 nm). A base pressure of 5x10-6 torr was demon- Exploration Research Virtual Institute) node. TREX strated by the vendor, without inclusion of any geolog- (trex.psi.edu) aims to decrease risk to future missions, ic samples. The useable wavelength range is 115-600 specifically to the Moon, the Martian moons, and near- nm. Earth asteroids, by improving mission success and A 30 W deuterium (D2) lamp provides illumination assuring the safety of astronauts, their instruments, and for the spectral range 115-250 nm. Longer wave- spacecraft. TREX studies will focus on characteristics lengths are attained with either a 100 W quartz- of the fine grains that cover the surfaces of these target tungsten-halogen (QTH) lamp or a 150 W xenon arc bodies – their spectral characteristics and the potential lamp; which of these sources to baseline is currently resources (such as H2O) they may harbor. TREX stud- under evaluation. A condenser using a concave mirror ies are organized into four Themes: lab studies [1], images a source to the spectrometer entrance slit. -

38782 3681 Scientific Equip-Spectrometers
NEW YORK STATE OFFICE OF GENERAL SERVICES PROCUREMENT SERVICES GROUP 38th Floor - Corning Tower Building Empire State Plaza Albany, New York 12242 http://www.ogs.state.ny.us Contract Award Notification Title : Group 38782 - SCIENTIFIC EQUIPMENT - SPECTROMETERS, SPECTROPHOTO- METERS, RELATED EQUIPMENT AND ACCESSORIES Award Number : 3681-G (Replaces 1470) Contract Period : March 1, 1999 - February 28, 2001 Bid Opening Date : November 6, 1998 Date of Issue : March 22, 1999 Specification Reference : As Incorporated in the Invitation for Bids Address Inquiries To: All State Agencies Non-State Agencies Name : Sue Wolslegel Name : Judy Gibbons Title : Purchasing Officer Title : Purchase Coordinator Phone : 518-473-9441 Phone : 518-474-6717 Fax : 518-474-1563 Fax : 518-474-2437 E-mail : [email protected] E-mail : [email protected] Description This award covers several manufacturers lines of spectrometers, spectrophotometers, related equipment and accessories. Some dedicated instruments using spectrophotometric techniques (eg. CN, Hg, TOC analyzers) are also included. PR # 9525-T (continued) 9525ta.doc/5map/sw GROUP 38782 - Scientific Equipment - Spectrometers, AWARD PAGE 2 Spectrophotometers, Related Equipment and Accessories ________________________________________________________________________ CONTRACT # CONTRACTOR & ADDRESS TELEPHONE # FED.IDENT.# PC54762 AMERSHAM PHARMACIA (800) 526-3593 36-2656030 BIOTECH INC. (732) 457-8000 800 Centennial Ave. Maria Hush Piscataway, NJ 08855 FAX: (800) 329-3593 (732) 457-8310 Web site: www.apbiotech.com PC54763 BECKMAN COULTER, INC. (800) 742-2345 95-1040600 4300 N. Harbor Blvd., E-28-C Gerald Reynolds Fullerton, CA 92834-3100 FAX: (800) 643-4366 PC54764 BRUKER AXS, INC. (800) 234-9729 39-1908020 6300 Enterprise Lane (608) 276-3000 Madison, WI 53719 David Melton (608) 276-3006 PC54765 BRUKER INSTRUMENTS, INC. -

320-Channel Dual Phase Lock-In Optical Spectrometer
Cleveland State University EngagedScholarship@CSU Physics Faculty Publications Physics Department 2005 320-Channel Dual Phase Lock-in Optical Spectrometer Petru S. Fodor Cleveland State University, [email protected] S. Rothenberger University of Pittsburgh J. Levy University of Pittsburgh Follow this and additional works at: https://engagedscholarship.csuohio.edu/sciphysics_facpub Part of the Physics Commons How does access to this work benefit ou?y Let us know! Repository Citation Fodor, Petru S.; Rothenberger, S.; and Levy, J., "320-Channel Dual Phase Lock-in Optical Spectrometer" (2005). Physics Faculty Publications. 199. https://engagedscholarship.csuohio.edu/sciphysics_facpub/199 This Article is brought to you for free and open access by the Physics Department at EngagedScholarship@CSU. It has been accepted for inclusion in Physics Faculty Publications by an authorized administrator of EngagedScholarship@CSU. For more information, please contact [email protected]. 320-channel dual phase lock-in optical spectrometer P. S. Fodor, S. Rothenberger, and J. Jevy Citation: Rev. Sci. Instrum. 76, 013103 (2005); doi: 10.1063/1.1830013 View online: http://dx.doi.org/10.1063/1.1830013 View Table of Contents: http://aip.scitation.org/toc/rsi/76/1 Published by the American Institute of Physics REVIEW OF SCIENTIFIC INSTRUMENTS 76, 013103 (2005) 320-channel dual phase lock-in optical spectrometer P. S. Fodor,a) S. Rothenberger, and J. Jevy Department of Physics and Astronomy, University of Pittsburgh, 3941 O’Hara Street, Pittsburgh, Pennsylvania 15260 (Received 6 May 2004; accepted 11 October 2004; published online 20 December 2004) The development of a multiple-channel lock-in optical spectrometer (LIOS) is presented, which enables parallel phase-sensitive detection at the output of an optical spectrometer. -

High Resolution Spectrometer Model
Model 209 High Resolution Spectrometer SPECIAL FEATURES • Exceptional Spectral Resolution • Patented "Snap-In" gratings • Large focal plane • Imaging Optics • Multiple slit locations • Rugged Construction • Extended wavelength range setting • Double Pass optics (option) • Echelle gratings(option) • Prism predisperser (option) DETAIL SPECIFICATION AND GRATING SELECTION Focal Length 1.33-meter, Czerny Turner design Spectrometer with Patented "Snap-In" gratings Slit Locations Axial and lateral with optional extra entrance and exit port selection mirrors f No. 9.4 (11.6 with smaller grating) Grating Size 120 x 140-mm (or 110 x 110-mm) - Echelle gratings up to 220-mm wide Accuracy 0.05 nm (with 1200-g/mm grating) Reproducibility ±0.005 nm (with 1200-g/mm grating) Focal Plane 50-mm maximum width, multiply dispersion by the width of your detector for range Wavelength Range refer to grating of interest for range, in extended position increase top limit 20% Grating Groove Density (g/mm) 3600 2400 1800 1200 600 300 150 75 Resolution** (nm) 0.004 0.005 0.007 0.01 0.02 0.04 0.08 0.16 Dispersion (nm/mm) 0.21 0.31 0.41 0.62 1.24 2.48 4.96 9.92 Wavelength Range 185 - 185 - 185 - 185 - 185 - 185 nm 185 nm 185 nm 430 nm 650 nm 860 nm 1300 nm 2600 nm 5.2 um 10.4 um 20.8 um Available Grating Holographic* Holographic* Holographic* Holographic* Holographic* Blazes 240 240 400 250 300 300 300 2 um 300 500 300 500 500 500 3 um (* Holographic gratings are 500 750 750 1.25 um 8 um available where noted.) 750 1 um 1 um 2.5 um 10 um 1 um 1.85 um 3 um 4 um 12 um 4 um 6 um 8 um ** Spectral resolution typically measured at 313.1 nm All specifications are for single pass operation. -

Master Catalog
Spectrometers, Monochromators & Spectrographs Soft X-ray Extreme Ultraviolet Vacuum Ultraviolet Deep UV Ultraviolet Visible Near Infrared Mid-wave Infrared Long-wave Infrared Master Catalog Spectral analysis systems Astrophysics Calibration Atomic Emission in Vacuum UV Cathodoluminescence Microscopy Chemiluminescence Since 1953 Double Spectrometers for Radiometry Fluorescence, Steady State and Dynamic Flow High Throughput Spectrometers Imaging Spectrometers Photoluminescence Phosphorescence Raman, Triple Stage Research Tools Raman, Single Stage Analytical Tools Reflectometry Remote Spectral Sensing Spectral Test Stations Spectrophotometry UV-Visible and Infrared Spectrophotometry Vacuum Ultraviolet Micro Spectroscopy Cathodoluminescence Ultrafast Compensated Path Spectrometers Instruments Made to Measure Light, for a You have choices when it comes to selecting tools to measure Solution oriented systems provide for fluorescence, Raman, light. Our mission is to make your choice simple, to provide luminescence, microscopy, thermonuclear fusion diagnostics, solutions for challenging spectroscopy applications, to deliver astrophysics calibration and more. You are the scientific ex- quality equipment you can rely on, and information to help perts. We hope to influence your work by delivering high make your buying decisions simple. quality, unique and effective instrumentation that improves every result. Application: Raman Spectroscopy What to use: Triple Spectrometer 2035 Subtractive + Model 207 = UV capable, tunable, awesome rejection of scatter and phenomenal f/4.8 aperture. The best light gathering power. (more about our Triple Monochromators on page 11) Application: Vacuum Ultraviolet Spectroscopy What to use: 234/302 Model 234/302 simplifies work from 30-nm to the Visible. It is good all around. Its affordable and works with CCD & scanning detectors. (more about our vacuum spectrometers on page 21) 2 World of Applications. -

Planetary Science Institute Spectroscopy Lab Annual Report for 2017 Prepared by Neil Pearson
Planetary Science Institute Spectroscopy Lab Annual Report for 2017 prepared by Neil Pearson Summary In October of 2017 Neil Pearson was hired as the Lab Technician for the Planetary Science Institute (PSI), with the primary purpose to run and upkeep equipment that was purchased by PSI and its associated scientists. This report will cover activities between October, November and December of 2017. The spectroscopy lab currently has three main instruments in house and a fourth that is with Dr. Eldar Noe Dobrea at NASA Ames. The three instruments currently at PSI are the Andor-McPherson Vacuum Ultraviolet (VUV) Spectrometer, the Ocean Optics Ultraviolet to Visible spectrometer, and the Analytical Spectral Devices (ASD) Fieldspec 3 visible to short wave infrared spectrometer. Dr. Eldar Noe Dobrea has in his possession an Olympus Terra X-ray diffractomeer and X-ray fluoresence spectrometer. Additionaly, the lab contains and high vacuum chamber for measuring samples in space like conditions. Efforts since October have focused on tuning and calibrating instruments, and preparing the laboratory for measuring samples for the Toolbox for Research and Exploration project headed by PSI’s Dr. Amanda Hendrix, and investigating reflectance standards for the vacuum-UV Currently two abstracts were submitted to the 2018 Lunar and Planetary Science Conference that will use spectra taken at the PSI spectroscopy lab. Laboratory Instruments The Andor-McPherson VUV spectrometer is the most unique instrument at the PSI spectroscopy lab. This instrument combines a Andor Solis cooled silicon detector array with a McPherson Inc. Monochrometer and 300 line/mm grating. The VUV spectrometer measures reflectance of minerals samples in the VUV down to ~0.115μm and in its normal operating mode goes to 0.4μm with a spectral resolution of 8nm.