DOCSLIB.ORG

Optimization Methods in Finance

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Optimization Methods in Finance Optimization Methods in Finance Gerard Cornuejols Reha Tut¨ unc¨ u¨ Carnegie Mellon University, Pittsburgh, PA 15213 USA January 2006 2 Foreword Optimization models play an increasingly important role in financial de- cisions. Many computational finance problems ranging from asset allocation to risk management, from option pricing to model calibration can be solved efficiently using modern optimization techniques. This course discusses sev- eral classes of optimization problems (including linear, quadratic, integer, dynamic, stochastic, conic, and robust programming) encountered in finan- cial models. For each problem class, after introducing the relevant theory (optimality conditions, duality, etc.) and efficient solution methods, we dis- cuss several problems of mathematical finance that can be modeled within this problem class. In addition to classical and well-known models such as Markowitz' mean-variance optimization model we present some newer optimization models for a variety of financial problems. Acknowledgements This book has its origins in courses taught at Carnegie Mellon University in the Masters program in Computational Finance and in the MBA program at the Tepper School of Business (G´erard Cornu´ejols), and at the Tokyo In- stitute of Technology, Japan, and the University of Coimbra, Portugal (Reha Tut¨ unc¨ u).¨ We thank the attendants of these courses for their feedback and for many stimulating discussions. We would also like to thank the colleagues who provided the initial impetus for this project, especially Michael Trick, John Hooker, Sanjay Srivastava, Rick Green, Yanjun Li, Lu´ıs Vicente and Masakazu Kojima. Various drafts of this book were experimented with in class by Javier Pena,~ Fran¸cois Margot, Miroslav Karamanov and Kathie Cameron, and we thank them for their comments. Contents 1 Introduction 9 1.1 Optimization Problems . 9 1.1.1 Linear and Nonlinear Programming . 10 1.1.2 Quadratic Programming . 11 1.1.3 Conic Optimization . 12 1.1.4 Integer Programming . 12 1.1.5 Dynamic Programming . 13 1.2 Optimization with Data Uncertainty . 13 1.2.1 Stochastic Programming . 13 1.2.2 Robust Optimization . 14 1.3 Financial Mathematics . 16 1.3.1 Portfolio Selection and Asset Allocation . 16 1.3.2 Pricing and Hedging of Options . 18 1.3.3 Risk Management . 19 1.3.4 Asset/Liability Management . 20 2 Linear Programming: Theory and Algorithms 23 2.1 The Linear Programming Problem . 23 2.2 Duality . 25 2.3 Optimality Conditions . 28 2.4 The Simplex Method . 31 2.4.1 Basic Solutions . 32 2.4.2 Simplex Iterations . 35 2.4.3 The Tableau Form of the Simplex Method . 39 2.4.4 Graphical Interpretation . 42 2.4.5 The Dual Simplex Method . 43 2.4.6 Alternatives to the Simplex Method . 45 3 LP Models: Asset/Liability Cash Flow Matching 47 3.1 Short Term Financing . 47 3.1.1 Modeling . 48 3.1.2 Solving the Model with SOLVER . 50 3.1.3 Interpreting the output of SOLVER . 53 3.1.4 Modeling Languages . 54 3.1.5 Features of Linear Programs . 55 3.2 Dedication . 56 3.3 Sensitivity Analysis for Linear Programming . 58 3 4 CONTENTS 3.3.1 Short Term Financing . 58 3.3.2 Dedication . 63 3.4 Case Study . 66 4 LP Models: Asset Pricing and Arbitrage 69 4.1 The Fundamental Theorem of Asset Pricing . 69 4.1.1 Replication . 71 4.1.2 Risk-Neutral Probabilities . 72 4.1.3 The Fundamental Theorem of Asset Pricing . 74 4.2 Arbitrage Detection Using Linear Programming . 75 4.3 Additional Exercises . 78 4.4 Case Study: Tax Clientele Effects in Bond Portfolio Manage- ment . 82 5 Nonlinear Programming: Theory and Algorithms 85 5.1 Introduction . 85 5.2 Software . 87 5.3 Univariate Optimization . 88 5.3.1 Binary search . 88 5.3.2 Newton's Method . 92 5.3.3 Approximate Line Search . 95 5.4 Unconstrained Optimization . 97 5.4.1 Steepest Descent . 97 5.4.2 Newton's Method . 101 5.5 Constrained Optimization . 104 5.5.1 The generalized reduced gradient method . 107 5.5.2 Sequential Quadratic Programming . 112 5.6 Nonsmooth Optimization: Subgradient Methods . 113 6 NLP Models: Volatility Estimation 115 6.1 Volatility Estimation with GARCH Models . 115 6.2 Estimating a Volatility Surface . 119 7 Quadratic Programming: Theory and Algorithms 125 7.1 The Quadratic Programming Problem . 125 7.2 Optimality Conditions . 126 7.3 Interior-Point Methods . 128 7.4 The Central Path . 131 7.5 Interior-Point Methods . 132 7.5.1 Path-Following Algorithms . 132 7.5.2 Centered Newton directions . 133 7.5.3 Neighborhoods of the Central Path . 135 7.5.4 A Long-Step Path-Following Algorithm . 138 7.5.5 Starting from an Infeasible Point . 138 7.6 QP software . 139 7.7 Additional Exercises . 139 CONTENTS 5 8 QP Models: Portfolio Optimization 141 8.1 Mean-Variance Optimization . 141 8.1.1 Example . 143 8.1.2 Large-Scale Portfolio Optimization . 148 8.1.3 The Black-Litterman Model . 151 8.1.4 Mean-Absolute Deviation to Estimate Risk . 155 8.2 Maximizing the Sharpe Ratio . 158 8.3 Returns-Based Style Analysis . 160 8.4 Recovering Risk-Neural Probabilities from Options Prices . 162 8.5 Additional Exercises . 166 8.6 Case Study . 168 9 Conic Optimization Tools 171 9.1 Introduction . 171 9.2 Second-order cone programming: . 171 9.2.1 Ellipsoidal Uncertainty for Linear Constraints . 173 9.2.2 Conversion of quadratic constraints into second-order cone constraints . 175 9.3 Semidefinite programming: . 176 9.3.1 Ellipsoidal Uncertainty for Quadratic Constraints . 178 9.4 Algorithms and Software . 179 10 Conic Optimization Models in Finance 181 10.1 Tracking Error and Volatility Constraints . 181 10.2 Approximating Covariance Matrices . 184 10.3 Recovering Risk-Neural Probabilities from Options Prices . 187 10.4 Arbitrage Bounds for Forward Start Options . 189 10.4.1 A Semi-Static Hedge . 190 11 Integer Programming: Theory and Algorithms 195 11.1 Introduction . 195 11.2 Modeling Logical Conditions . 196 11.3 Solving Mixed Integer Linear Programs . 199 11.3.1 Linear Programming Relaxation . 199 11.3.2 Branch and Bound . 200 11.3.3 Cutting Planes . 208 11.3.4 Branch and Cut . 212 12 IP Models: Constructing an Index Fund 215 12.1 Combinatorial Auctions . 215 12.2 The Lockbox Problem . 216 12.3 Constructing an Index Fund . 219 12.3.1 A Large-Scale Deterministic Model . 220 12.3.2 A Linear Programming Model . 223 12.4 Portfolio Optimization with Minimum Transaction Levels . 224 12.5 Exercises . 225 12.6 Case Study . 226 6 CONTENTS 13 Dynamic Programming Methods 227 13.1 Introduction . 227 13.1.1 Backward Recursion . 230 13.1.2 Forward Recursion . 233 13.2 Abstraction of the Dynamic Programming Approach . 234 13.3 The Knapsack Problem. 237 13.3.1 Dynamic Programming Formulation . 237 13.3.2 An Alternative Formulation . 238 13.4 Stochastic Dynamic Programming . 239 14 DP Models: Option Pricing 241 14.1 A Model for American Options . 241 14.2 Binomial Lattice . 243 14.2.1 Specifying the parameters . 244 14.2.2 Option Pricing . 245 15 DP Models: Structuring Asset Backed Securities 249 15.1 Data . 251 15.2 Enumerating possible tranches . 253 15.3 A Dynamic Programming Approach . 254 15.4 Case Study . 255 16 Stochastic Programming: Theory and Algorithms 257 16.1 Introduction . 257 16.2 Two Stage Problems with Recourse . 258 16.3 Multi Stage Problems . 260 16.4 Decomposition . 262 16.5 Scenario Generation . 265 16.5.1 Autoregressive model . 265 16.5.2 Constructing scenario trees . 267 17 SP Models: Value-at-Risk 273 17.1 Risk Measures . 273 17.2 Minimizing CVaR . 276 17.3 Example: Bond Portfolio Optimization . 278 18 SP Models: Asset/Liability Management 281 18.1 Asset/Liability Management . 281 18.1.1 Corporate Debt Management . 284 18.2 Synthetic Options . 287 18.3 Case Study: Option Pricing with Transaction Costs . 290 18.3.1 The Standard Problem . 291 18.3.2 Transaction Costs . 292 19 Robust Optimization: Theory and Tools 295 19.1 Introduction to Robust Optimization . 295 19.2 Uncertainty Sets . 296.
Load more

Recommended publications
  • Researchers in Computational Finance / Quant Portfolio Analysts Limassol, Cyprus
    Researchers in Computational Finance / Quant Portfolio Analysts Limassol, Cyprus Award winning Hedge Fund is seeking to build their team with top researchers to join their offices in Limassol, Cyprus. IKOS is an investment advisor that deploys quantitative hedge fund strategies to trade the global financial markets, with a long and successful track record. This is an exciting opportunity to join a fast growing company that is focused on the development of the best research and trading infrastructure. THE ROLE We are looking for top class mathematicians to work with us in modern quantitative finance. Our researchers participate in novel financial analysis and development efforts that require significant application of mathematical modelling techniques. The position involves working within the Global Research team; there is also significant interaction with the trading and fund management teams. The objective is the development of innovative products and computational methods in the equities, futures, currency and fixed income markets. In addition, the role involves statistical analysis of portfolio risk and returns, involvement in the portfolio management process and monitoring and analysing transactions on an ongoing basis. THE INDIVIDUAL The successful candidates will have a first class degree and practical science or engineering problem solving skills through a PhD in mathematics or mathematical sciences, together with excellent all round analytical and programming abilities. The following skills are also prerequisites for the job:
    [Show full text]
  • Master of Science in Finance (MSF) 1
    Master of Science in Finance (MSF) 1 MASTER OF SCIENCE IN FINANCE (MSF) MSF 501 MSF 505 Mathematics with Financial Applications Futures, Options, and OTC Derivatives This course provides a systematic exposition of the primary This course provides the foundation for understanding the price mathematical methods used in financial economics. Mathematical and risk management of derivative securities. The course starts concepts and methods include logarithmic and exponential with simple derivatives, e.g., forwards and futures, and develops functions, algebra, mean-variance analysis, summations, matrix the concept of arbitrage-free pricing and hedging. Based upon algebra, differential and integral calculus, and optimization. The the work of Black, Scholes, and Merton, the course extends their course will include a variety of financial applications including pricing model through the use of lattices, Monte Carlo simulation compound interest, present and future value, term structure of methods, and more advanced strategies. Mathematical tools in interest rates, asset pricing, expected return, risk and measures stochastic processes are gradually introduced throughout the of risk aversion, capital asset pricing model (CAPM), portfolio course. Particular emphasis is given to the pricing of interest rate optimization, expected utility, and consumption capital asset pricing derivatives, e.g., FRAs, swaps, bond options, caps, collars, and (CCAPM). floors. Lecture: 3 Lab: 0 Credits: 3 Prerequisite(s): MSF 501 with min. grade of C and MSF 503 with min. grade of C and MSF 502 with min. grade of C MSF 502 Lecture: 3 Lab: 0 Credits: 3 Statistical Analysis in Financial Markets This course presents and applies statistical and econometric MSF 506 techniques useful for the analysis of financial markets.
    [Show full text]
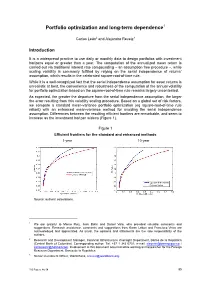
  • Portfolio Optimization and Long-Term Dependence1
    Portfolio optimization and long-term dependence1 Carlos León2 and Alejandro Reveiz3 Introduction It is a widespread practice to use daily or monthly data to design portfolios with investment horizons equal or greater than a year. The computation of the annualized mean return is carried out via traditional interest rate compounding – an assumption free procedure –, while scaling volatility is commonly fulfilled by relying on the serial independence of returns’ assumption, which results in the celebrated square-root-of-time rule. While it is a well-recognized fact that the serial independence assumption for asset returns is unrealistic at best, the convenience and robustness of the computation of the annual volatility for portfolio optimization based on the square-root-of-time rule remains largely uncontested. As expected, the greater the departure from the serial independence assumption, the larger the error resulting from this volatility scaling procedure. Based on a global set of risk factors, we compare a standard mean-variance portfolio optimization (eg square-root-of-time rule reliant) with an enhanced mean-variance method for avoiding the serial independence assumption. Differences between the resulting efficient frontiers are remarkable, and seem to increase as the investment horizon widens (Figure 1). Figure 1 Efficient frontiers for the standard and enhanced methods 1-year 10-year Source: authors’ calculations. 1 We are grateful to Marco Ruíz, Jack Bohn and Daniel Vela, who provided valuable comments and suggestions. Research assistance, comments and suggestions from Karen Leiton and Francisco Vivas are acknowledged and appreciated. As usual, the opinions and statements are the sole responsibility of the authors.
    [Show full text]
  • MIE 1612: Stochastic Programming and Robust Optimization
    MIE 1612: Stochastic Programming and Robust Optimization Fall 2019 Syllabus Instructor: Prof. Merve Bodur Office: BA8106 Office hour: Wednesday 2-3pm (or by appointment) E-mail: [email protected] P.S. Please include course code (MIE 1612) in your email subject TA: Maryam Daryalal Office hour: Monday 2:30-3:30pm, in BA8119 (or by appointment) E-mail: [email protected] P.S. Please include course code (MIE 1612) in your email subject Lectures: Monday 4-6pm (GB119) and Wednesday 1-2pm (GB303) Suggested texts: Lectures on Stochastic Programming { Modeling and Theory, SIAM, Shapiro, Dentcheva, and Ruszczy´nski,2009. Introduction to Stochastic Programming, Springer-Verlag, Birge and Louveaux, 2011. Stochastic Programming, Wiley, Kall and Wallace, 1994. Stochastic Programming, Handbooks in OR and MS, Elsevier, Ruszczy´nskiand Shapiro, 2003. Robust Optimization, Princeton University Press, Ben-Tal, El Ghaoui, and Nemirovski, 2009. Course web pages: Quercus, Piazza Official course description: Stochastic programming and robust optimization are optimization tools deal- ing with a class of models and algorithms in which data is affected by uncertainty, i.e., some of the input data are not perfectly known at the time the decisions are made. Topics include modeling uncertainty in optimization problems, two-stage and multistage stochastic programs with recourse, chance constrained pro- grams, computational solution methods, approximation and sampling methods, and applications. Knowledge of linear programming, probability and statistics are required, while programming ability and knowledge of integer programming are helpful. Prerequisite: MIE262, APS1005 or equivalent, and MIE231, APS106S or equivalent. 1 Overview The aim of stochastic programming and robust optimization is to find optimal decisions in problems which involve uncertain data.
    [Show full text]
  • From Arbitrage to Arbitrage-Free Implied Volatilities
    Journal of Computational Finance 20(3), 31–49 DOI: 10.21314/JCF.2016.316 Research Paper From arbitrage to arbitrage-free implied volatilities Lech A. Grzelak1,2 and Cornelis W. Oosterlee1,3 1Delft Institute of Applied Mathematics, Delft University of Technology, Mekelweg 4, 2628 CD, Delft, The Netherlands; email: [email protected] 2ING, Quantiative Analytics, Bijlmerplein 79, 1102 BH, Amsterdam, The Netherlands 3CWI: National Research Institute for Mathematics and Computer Science, Science Park 123, 1098 XG, Amsterdam, The Netherlands; email: [email protected] (Received October 14, 2015; revised March 6, 2016; accepted March 7, 2016) ABSTRACT We propose a method for determining an arbitrage-free density implied by the Hagan formula. (We use the wording “Hagan formula” as an abbreviation of the Hagan– Kumar–Le´sniewski–Woodward model.) Our method is based on the stochastic collo- cation method. The principle is to determine a few collocation points on the implied survival distribution function and project them onto the polynomial of an arbitrage- free variable for which we choose the Gaussian variable. In this way, we have equality in probability at the collocation points while the generated density is arbitrage free. Analytic European option prices are available, and the implied volatilities stay very close to those initially obtained by the Hagan formula. The proposed method is very fast and straightforward to implement, as it only involves one-dimensional Lagrange interpolation and the inversion of a linear system of equations. The method is generic and may be applied to other variants or other models that generate arbitrage. Keywords: arbitrage-free density; collocation method; orthogonal projection; arbitrage-free volatility; SCMC sampler; implied volatility parameterization.
    [Show full text]
  • Careers in Quantitative Finance by Steven E
    Careers in Quantitative Finance by Steven E. Shreve1 August 2018 1 What is Quantitative Finance? Quantitative finance as a discipline emerged in the 1980s. It is also called financial engineering, financial mathematics, mathematical finance, or, as we call it at Carnegie Mellon, computational finance. It uses the tools of mathematics, statistics, and computer science to solve problems in finance. Computational methods have become an indispensable part of the finance in- dustry. Originally, mathematical modeling played the dominant role in com- putational finance. Although this continues to be important, in recent years data science and machine learning have become more prominent. Persons working in the finance industry using mathematics, statistics and computer science have come to be known as quants. Initially relegated to peripheral roles in finance firms, quants have now taken center stage. No longer do traders make decisions based solely on instinct. Top traders rely on sophisticated mathematical models, together with analysis of the current economic and financial landscape, to guide their actions. Instead of sitting in front of monitors \following the market" and making split-second decisions, traders write algorithms that make these split- second decisions for them. Banks are eager to hire \quantitative traders" who know or are prepared to learn this craft. While trading may be the highest profile activity within financial firms, it is not the only critical function of these firms, nor is it the only place where quants can find intellectually stimulating and rewarding careers. I present below an overview of the finance industry, emphasizing areas in which quantitative skills play a role.
    [Show full text]
  • Financial Mathematics
    Financial Mathematics Alec Kercheval (Chair, Florida State University) Ronnie Sircar (Princeton University) Jim Sochacki (James Madison University) Tim Sullivan (Economics, Towson University) Introduction Financial Mathematics developed in the mid-1980s as research mathematicians became interested in problems, largely involving stochastic control, that had until then been studied primarily by economists. The subject grew slowly at first and then more rapidly from the mid- 1990s through to today as mathematicians with backgrounds first in probability and control, then partial differential equations and numerical analysis, got into it and discovered new issues and challenges. A society of mostly mathematicians and some economists, the Bachelier Finance Society, began in 1997 and holds biannual world congresses. The Society for Industrial and Applied Mathematics (SIAM) started an Activity Group in Financial Mathematics & Engineering in 2002; it now has about 800 members. The 4th SIAM conference in this area was held jointly with its annual meeting in Minneapolis in 2013, and attracted over 300 participants to the Financial Mathematics meeting. In 2009 the SIAM Journal on Financial Mathematics was launched and it has been very successful gauged by numbers of submissions. Student interest grew enormously over the same period, fueled partly by the growing financial services sector of modern economies. This growth created a demand first for quantitatively trained PhDs (typically physicists); it then fostered the creation of a large number of Master’s programs around the world, especially in Europe and in the U.S. At a number of institutions undergraduate programs have developed and become quite popular, either as majors or tracks within a mathematics major, or as joint degrees with Business or Economics.
    [Show full text]
  • Financial Engineering and Computational Finance with R Rmetrics Built 221.10065
    Rmetrics An Environment for Teaching Financial Engineering and Computational Finance with R Rmetrics Built 221.10065 Diethelm Würtz Institute for Theoretical Physics Swiss Federal Institute of Technology, ETH Zürich Rmetrics is a collection of several hundreds of functions designed and written for teaching "Financial Engineering" and "Computational Finance". Rmetrics was initiated in 1999 as an outcome of my lectures held on topics in econophysics at ETH Zürich. The family of the Rmetrics packages build on ttop of the statistical software environment R includes members dealing with the following subjects: fBasics - Markets and Basic Statistics, fCalendar - Date, Time and Calendar Management, fSeries - The Dynamical Process Behind Financial Markets, fMultivar - Multivariate Data Analysis, fExtremes - Beyond the Sample, Dealing with Extreme Values, fOptions – The Valuation of Options, and fPortfolio - Portfolio Selection and Optimization. Rmetrics has become the premier open source to download data sets from the Internet. The solution for financial market analysis and valu- major concern is given to financial return series ation of financial instruments. With hundreds of and their stylized facts. Distribution functions functions build on modern and powerful methods relevant in finance are added like the stable, the Rmetrics combines explorative data analysis and hyperbolic, or the normal inverse Gaussian statistical modeling with object oriented rapid distribution function to compute densities, pro- prototyping. Rmetrics is embedded in R, both babilities, quantiles and random deviates. Esti- building an environment which creates especially mators to fit the distributional parameters are for students and researchers in the third world a also available. Furthermore, hypothesis tests for first class system for applications in statistics and the investigation of distributional properties, of finance.
    [Show full text]
  • A Multi-Objective Approach to Portfolio Optimization
    Rose-Hulman Undergraduate Mathematics Journal Volume 8 Issue 1 Article 12 A Multi-Objective Approach to Portfolio Optimization Yaoyao Clare Duan Boston College, [email protected] Follow this and additional works at: https://scholar.rose-hulman.edu/rhumj Recommended Citation Duan, Yaoyao Clare (2007) "A Multi-Objective Approach to Portfolio Optimization," Rose-Hulman Undergraduate Mathematics Journal: Vol. 8 : Iss. 1 , Article 12. Available at: https://scholar.rose-hulman.edu/rhumj/vol8/iss1/12 A Multi-objective Approach to Portfolio Optimization Yaoyao Clare Duan, Boston College, Chestnut Hill, MA Abstract: Optimization models play a critical role in determining portfolio strategies for investors. The traditional mean variance optimization approach has only one objective, which fails to meet the demand of investors who have multiple investment objectives. This paper presents a multi- objective approach to portfolio optimization problems. The proposed optimization model simultaneously optimizes portfolio risk and returns for investors and integrates various portfolio optimization models. Optimal portfolio strategy is produced for investors of various risk tolerance. Detailed analysis based on convex optimization and application of the model are provided and compared to the mean variance approach. 1. Introduction to Portfolio Optimization Portfolio optimization plays a critical role in determining portfolio strategies for investors. What investors hope to achieve from portfolio optimization is to maximize portfolio returns and minimize portfolio risk. Since return is compensated based on risk, investors have to balance the risk-return tradeoff for their investments. Therefore, there is no a single optimized portfolio that can satisfy all investors. An optimal portfolio is determined by an investor’s risk-return preference.
    [Show full text]
  • Extending Algebraic Modelling Languages for Stochastic Programming
    Extending algebraic modelling languages for Stochastic Programming Christian Valente, Gautam Mitra, Mustapha Sadki CARISMA, Brunel University and OptiRisk Systems Uxbridge, Middlesex, UK Robert Fourer Northwestern University, Evanston, IL Abstract Algebraic modelling languages (AML) have gained wide acceptance and use in Mathematical Programming by researchers and practitioners. At a basic level, stochastic programming models can be defined using these languages by constructing their deterministic equivalent. Unfortunately, this leads to very large model data instances. We propose a direct approach in which the random values of the model coefficients and the stage structure of the decision variables and constraints are "overlaid" on the underlying deterministic (core) model of the SP problems. This leads not only to a natural definition of the SP model, the resulting generated instance is also a compact representation of the otherwise large problem data. The proposed constructs enable the formulation of two stage and multistage scenario based recourse problems. The design is presented as a stochastic extension of the AMPL language which we call SAMPL; this in turn is embedded in an environment called SPInE (Stochastic Programming Integrated Environment) which facilitates modelling and investigation of SP problems. Table of Contents 1 Introduction.............................................................................................................2 1.1 Background .................................................................................................................2
    [Show full text]
  • Computational Finance
    Computational Finance Christian Bayer & Antonis Papapantoleon Lecture course @ TU Berlin, SS 2013 Important information The course takes place every Monday 12:00{14:00 @ MA 751 Friday 10:00{12:00 @ MA 848 The website of the course is: http://www.math.tu-berlin.de/~papapan/ ComputationalFinance.html contains: course description, recommended literature, and other material related to the course Lecture notes are available on the website E-mails: [email protected] [email protected] Office: MA 703 Office hours: Tuesday 11-12 1 / 22 Structure of the course Teaching (per week): 3h Theory 1h Computational practice (Scilab) Exam: 3 Computational exercises Oral examination Credit points: 10 2 / 22 Key points of the course 1 Review of stochastic analysis and mathematical finance 2 Monte Carlo simulation Random number generation Monte Carlo method Quasi Monte Carlo method 3 Discretization of SDEs Generating sample paths Euler scheme Advanced methods (Milstein) 4 PDE methods (finite differences, finite elements) 5 L´evyand affine processes 6 Fourier methods 7 Pricing American options with Monte Carlo 3 / 22 Books P. Glasserman Monte Carlo Methods in Financial Engineering Springer, 2003 R. Seydel Tools for Computational Finance Springer, 2009 S. Shreve Stochastic Calculus for Finance II Springer, 2004 M. Musiela, M. Rutkowski Martingale Methods in Financial Modeling Springer, 2nd ed., 2005 D. Filipovi´c Term-structure Models: A Graduate Course Springer, 2009 4 / 22 Options European options \plain vanilla" options + call (ST K) − digital 1 ST >B f g exotic options + barrier (ST K) 1 maxt≤T St >B − f g one-touch 1 maxt≤T St >B 1 Pnf g+ Asian ( ST K) n i=1 i − options on several assets Pd i + basket call ( i=1 ST K) best-of call (S 1 − S d K)+ T ^ · · · ^ T − American options + call (Sτ K) − τ: stopping time 5 / 22 Decomposition of options Payoff function: Underlying process: d map f : R R+ random variable X on the path ! d f (x) = (x K)+ space D([0; T ]; R ) − X = S f (x) = 1fx>Bg T + X = max S f (x) = (x1+ +xd K) t≤T t ··· − 1 d ..
    [Show full text]
  • Achieving Portfolio Diversification for Individuals with Low Financial
    sustainability Article Achieving Portfolio Diversification for Individuals with Low Financial Sustainability Yongjae Lee 1 , Woo Chang Kim 2 and Jang Ho Kim 3,* 1 Department of Industrial Engineering, Ulsan National Institute of Science and Technology (UNIST), Ulsan 44919, Korea; [email protected] 2 Department of Industrial and Systems Engineering, Korea Advanced Institute of Science and Technology (KAIST), Daejeon 34141, Korea; [email protected] 3 Department of Industrial and Management Systems Engineering, Kyung Hee University, Yongin-si 17104, Gyeonggi-do, Korea * Correspondence: [email protected] Received: 5 August 2020; Accepted: 26 August 2020; Published: 30 August 2020 Abstract: While many individuals make investments to gain financial stability, most individual investors hold under-diversified portfolios that consist of only a few financial assets. Lack of diversification is alarming especially for average individuals because it may result in massive drawdowns in their portfolio returns. In this study, we analyze if it is theoretically feasible to construct fully risk-diversified portfolios even for the small accounts of not-so-rich individuals. In this regard, we formulate an investment size constrained mean-variance portfolio selection problem and investigate the relationship between the investment amount and diversification effect. Keywords: portfolio size; portfolio diversification; individual investor; financial sustainability 1. Introduction Achieving financial sustainability is a basic goal for everyone and it has become a shared concern globally due to increasing life expectancy. Low financial sustainability may refer to individuals with low financial wealth, as well as investors with a lack of financial literacy. Especially for individuals with limited wealth, financial sustainability after retirement is a real concern because of uncertainty in pension plans arising from relatively early retirement age and change in the demographic structure (see, for example, [1,2]).
    [Show full text]