Session 1 Regression Analysis Basics
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

A Stepwise Regression Method and Consistent Model Selection for High-Dimensional Sparse Linear Models
Submitted to the Annals of Statistics arXiv: math.PR/0000000 A STEPWISE REGRESSION METHOD AND CONSISTENT MODEL SELECTION FOR HIGH-DIMENSIONAL SPARSE LINEAR MODELS BY CHING-KANG ING ∗ AND TZE LEUNG LAI y Academia Sinica and Stanford University We introduce a fast stepwise regression method, called the orthogonal greedy algorithm (OGA), that selects input variables to enter a p-dimensional linear regression model (with p >> n, the sample size) sequentially so that the selected variable at each step minimizes the residual sum squares. We derive the convergence rate of OGA as m = mn becomes infinite, and also develop a consistent model selection procedure along the OGA path so that the resultant regression estimate has the oracle property of being equivalent to least squares regression on an asymptotically minimal set of relevant re- gressors under a strong sparsity condition. 1. Introduction. Consider the linear regression model p X (1.1) yt = α + βjxtj + "t; t = 1; 2; ··· ; n; j=1 with p predictor variables xt1; xt2; ··· ; xtp that are uncorrelated with the mean- zero random disturbances "t. When p is larger than n, there are computational and statistical difficulties in estimating the regression coefficients by standard regres- sion methods. Major advances to resolve these difficulties have been made in the past decade with the introduction of L2-boosting [2], [3], [14], LARS [11], and Lasso [22] which has an extensive literature because much recent attention has fo- cused on its underlying principle, namely, l1-penalized least squares. It has also been shown that consistent estimation of the regression function > > > (1.2) y(x) = α + β x; where β = (β1; ··· ; βp) ; x = (x1; ··· ; xp) ; is still possible under a sparseness condition on the regression coefficients. -

Stepwise Versus Hierarchical Regression: Pros and Cons
Running head: Stepwise versus Hierarchal Regression Stepwise versus Hierarchical Regression: Pros and Cons Mitzi Lewis University of North Texas Paper presented at the annual meeting of the Southwest Educational Research Association, February 7, 2007, San Antonio. Stepwise versus Hierarchical Regression, 2 Introduction Multiple regression is commonly used in social and behavioral data analysis (Fox, 1991; Huberty, 1989). In multiple regression contexts, researchers are very often interested in determining the “best” predictors in the analysis. This focus may stem from a need to identify those predictors that are supportive of theory. Alternatively, the researcher may simply be interested in explaining the most variability in the dependent variable with the fewest possible predictors, perhaps as part of a cost analysis. Two approaches to determining the quality of predictors are (1) stepwise regression and (2) hierarchical regression. This paper will explore the advantages and disadvantages of these methods and use a small SPSS dataset for illustration purposes. Stepwise Regression Stepwise methods are sometimes used in educational and psychological research to evaluate the order of importance of variables and to select useful subsets of variables (Huberty, 1989; Thompson, 1995). Stepwise regression involves developing a sequence of linear models that, according to Snyder (1991), can be viewed as a variation of the forward selection method since predictor variables are entered one at a Stepwise versus Hierarchical Regression, 3 time, but true stepwise entry differs from forward entry in that at each step of a stepwise analysis the removal of each entered predictor is also considered; entered predictors are deleted in subsequent steps if they no longer contribute appreciable unique predictive power to the regression when considered in combination with newly entered predictors (Thompson, 1989). -

Stepwise Model Fitting and Statistical Inference: Turning Noise Into Signal Pollution
Stepwise Model Fitting and Statistical Inference: Turning Noise into Signal Pollution The Harvard community has made this article openly available. Please share how this access benefits you. Your story matters Citation Mundry, Roger and Charles Nunn. 2009. Stepwise model fitting and statistical inference: turning noise into signal pollution. American Naturalist 173(1): 119-123. Published Version doi:10.1086/593303 Citable link http://nrs.harvard.edu/urn-3:HUL.InstRepos:5344225 Terms of Use This article was downloaded from Harvard University’s DASH repository, and is made available under the terms and conditions applicable to Open Access Policy Articles, as set forth at http:// nrs.harvard.edu/urn-3:HUL.InstRepos:dash.current.terms-of- use#OAP * Manuscript Stepwise model fitting and statistical inference: turning noise into signal pollution Roger Mundry1 and Charles Nunn1,2,3 1: Max Planck Institute for Evolutionary Anthropology Deutscher Platz 6 D-04103 Leipzig 2: Department of Integrative Biology University of California Berkeley, CA 94720-3140 USA 3: Department of Anthropology Harvard University Cambridge, MA 02138 USA Roger Mundry: [email protected] Charles L. Nunn: [email protected] Keywords: stepwise modeling, statistical inference, multiple testing, error-rate, multiple regression, GLM Article type: note elements of the manuscript that will appear in the expanded online edition: app. A, methods 1 Abstract Statistical inference based on stepwise model selection is applied regularly in ecological, evolutionary and behavioral research. In addition to fundamental shortcomings with regard to finding the 'best' model, stepwise procedures are known to suffer from a multiple testing problem, yet the method is still widely used. -

Why Stepwise and Similar Selection Methods Are Bad, and What You Should Use Peter L
NESUG 2007 Statistics and Data Analysis Stopping stepwise: Why stepwise and similar selection methods are bad, and what you should use Peter L. Flom, National Development and Research Institutes, New York, NY David L. Cassell, Design Pathways, Corvallis, OR ABSTRACT A common problem in regression analysis is that of variable selection. Often, you have a large number of potential independent variables, and wish to select among them, perhaps to create a ‘best’ model. One common method of dealing with this problem is some form of automated procedure, such as forward, backward, or stepwise selection. We show that these methods are not to be recommended, and present better alternatives using PROC GLMSELECT and other methods. Keywords: Regression selection forward backward stepwise glmselect. INTRODUCTION In this paper, we discuss variable selection methods for multiple linear regression with a single dependent variable y and a set of independent variables X1:p, according to y = Xβ + ε In particular, we discuss various stepwise methods (defined below) and with better alternatives as implemented in SAS R , version 9.1 and PROC GLMSELECT. Stepwise methods are also problematic for other types of regression, but we do not discuss these. The essential problems with stepwise methods have been admirably summarized by Frank Harrell in Regression Modeling Strategies Harrell (2001), and can be paraphrased as follows: 1. R2 values are biased high 2. The F and χ2 test statistics do not have the claimed distribution. 3. The standard errors of the parameter estimates are too small. 4. Consequently, the confidence intervals around the parameter estimates are too narrow. -

Economic Appraisal of the Commodity Vertical of Pork Market and Its Input Prices in the Czech Republic
1109 Bulgarian Journal of Agricultural Science, 26 (No 6) 2020, 1109–1115 Economic appraisal of the commodity vertical of pork market and its input prices in the Czech Republic Milan Palat1 and Sarka Palatova2 1NEWTON College, Private College of Economic Studies, Department of Economics, Brno, 602 00, Czech Republic 2Tomas Baa University in Zlin, Faculty of Management and Economics, Department of Management and Marketing, Zlin, 760 01, Czech Republic *Corresponding author: [email protected] Abstract Palat, M. & Palatova, S. (2020). Economic appraisal of the commodity vertical of pork market and its input prices in the Czech Republic. Bulg. J. Agric. Sci., 26 (6), 1109–1115 The aim of the article is to evaluate economic aspects of commodity verticals of pork market, including pigs for slaughter and pork meat taking into account input prices in the Czech Republic. In the Czech Republic, pig breeding and pork produc- tion had a traditional and significant position, which has been hampered by foreign competition in recent years. Czech pro- ducers can hardly compete with large enterprises from Germany or the Netherlands with modern infrastructure, concentrated production and are thus able to benefit from the economies of scale. Lower competitiveness of the Czech Republic in the production of pork reflects also in its high focus on imports. A result of several years of decline in the total number of pigs is high non-self-sufficiency of the Czech Republic in the production of pork and a high focus on imports. This is also evident from the calculated models of development trends in pork production in the Czech Republic. -

Variable Selection Using Stepwise Regression with Application to Mytherapistmatch.Com
University of California Los Angeles Variable Selection using Stepwise Regression with Application to MyTherapistMatch.com A thesis submitted in partial satisfaction of the requirements for the degree Master of Science in Statistics by Francesco Macchia 2012 c Copyright by Francesco Macchia 2012 Abstract of the Thesis Variable Selection using Stepwise Regression with Application to MyTherapistMatch.com by Francesco Macchia Master of Science in Statistics University of California, Los Angeles, 2012 Professor Frederic Paik Schoenberg, Chair MyTherapistMatch.com is a website that connects patients with therapists who are deemed to be well suited to patients' personality and mental health needs. The primary tool for this patient-therapist matching is an online questionnaire that is completed by users visiting the site. Only approximately ten percent of visitors to the site complete the questionnaire, ostensibly partly due to the exces- sive length of the survey. The purpose of this thesis is to identify the items on the questionnaire that have the greatest impact on how much users interact with the website and reach out to their therapist matches. This is done with linear regression techniques, including ordinary least squares regression and stepwise re- gression. According to the regression analyses, the single greatest determinant of user activity is whether the respondent lives in or outside of California. The pro- prietors of the website may use the results of this analysis in choosing a meaningful subset of items that forms a shorter questionnaire. ii The thesis of Francesco Macchia is approved. Robert L. Gould Nicolas Christou Frederic Paik Schoenberg, Committee Chair University of California, Los Angeles 2012 iii To my mother, for believing in me; to Cherine, for the years of friendship and encouragement; and to Ramon, for your love and unwavering support iv Table of Contents 1 Introduction :::::::::::::::::::::::::::::::: 1 2 Methods :::::::::::::::::::::::::::::::::: 3 2.1 Data . -

Backward Stepwise Regression
Backward Stepwise Regression BACKWARD STEPWISE REGRESSION is a stepwise regression approach that begins with a full (saturated) model and at each step gradually eliminates variables from the regression model to find a reduced model that best explains the data. Also known as Backward Elimination regression. The stepwise approach is useful because it reduces the number of predictors, reducing the multicollinearity problem and it is one of the ways to resolve the overfitting. How To Run: STATISTICS->REGRESSION -> BACKWARD STEPWISE REGRESSION... Select the DEPENDENT variable (RESPONSE) and INDEPENDENT variables (PREDICTORS). REMOVE IF ALPHA > option defines the Alpha-to-Remove value. At each step it is used to select candidate variables for elimination – variables, whose partial F p-value is greater or equal to the alpha-to-remove. The default value is 0.10. Select the SHOW CORRELATIONS option to include the correlation coefficients matrix to the report. Select the SHOW DESCRIPTIVE STATISTICS option to include the mean, variance and standard deviation of each term to the report. Select the SHOW RESULTS FOR EACH STEP option to show the regression model and summary statistics for each step. Results The report shows regression statistics for the final regression model. If the SHOW RESULTS FOR EACH STEP option is selected, the regression model, fit statistics and partial correlations are displayed at each removal step. Correlation coefficients matrix and descriptive statistics for predictors are displayed if the corresponding options are selected. The command removes predictors from the model in a stepwise manner. It starts from the full model with all variables added, at each step the predictor with the largest p-value (that is over the alpha-to-remove) is being eliminated. -
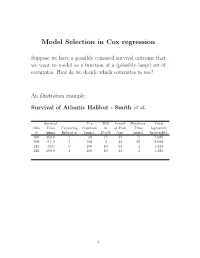
Model Selection in Cox Regression
Model Selection in Cox regression Suppose we have a possibly censored survival outcome that we want to model as a function of a (possibly large) set of covariates. How do we decide which covariates to use? An illustration example: Survival of Atlantic Halibut - Smith et al. Survival Tow Diff Length Handling Total Obs Time Censoring Duration in of Fish Time log(catch) # (min) Indicator (min.) Depth (cm) (min.) ln(weight) 100 353.0 1 30 15 39 5 5.685 109 111.0 1 100 5 44 29 8.690 113 64.0 0 100 10 53 4 5.323 116 500.0 1 100 10 44 4 5.323 . 1 Process of Model Selection There are various approaches to model selection. In practice, model selection proceeds through a combination of • knowledge of the science • trial and error, common sense • automated(?) variable selection procedures { forward selection { backward selection { stepwise selection • measures of explained variation • information criteria, eg. AIC, BIC, etc. • dimension reduction from high-d Many advocate the approach of first doing a univariate anal- ysis to \screen" out those variables that are likely noise. 2 (1) Stepwise (including forward, backward) pro- cedures have been very widely used in practice, and active research is still being carried out on post selection inference, etc. They are available as automated procedures in Stata and SAS, but currently there does not appear to be a rea- sonable one in R (the one based on AIC gives strange results, and is not recommended). We briefly describe the stepwise (back-n-forth) procedure there: (1) Fit a univariate model for each covariate, and identify the predictors significant at some level p1, say 0:20. -

Model Selection
Model Selection Frank Wood December 10, 2009 Standard Linear Regression Recipe I I Identify the explanatory variables I Decide the functional forms in which the explanatory variables can enter the model I Decide which interactions should be in the model. I Reduce explanatory variables (!?) I Refine model Trouble and Strife Form any set of p − 1 predictors, 2p−1 alternative linear regression models can be constructed I Consider all binary vectors of length p − 1 Search in that space is exponentially difficult. Greedy strategies are typically utilized. Is this the only way? Selecting between models In order to select between models some score must be given to each model. The likelihood of the data under each model is not sufficient because, as we have seen, the likelihood of the data can always be improved by adding more parameters until the model effectively memorizes the data. Accordingly some penalty that is a function of the complexity of the model must be included in the selection procedure. There are four choices for how to do this 1. Explicit penalization of the number of parameters in the model (AIC, BIC, etc.) 2. Implicit penalization through cross validation 3. Bayesian regularization / Occam's razor. 4. Use a fixed model of unbounded complexity (Bayesian nonparametrics). Penalized Likelihood The Akaike's information criterion (AIC) and the Bayesian information criterion (BIC) (also called the Schwarz criterion) are two criteria that penalize model complexity. In the linear regression setting AICp = n ln SSEp − l ln n + 2p 1 BICp = n ln SSEp − n ln n + (ln n)p Roughly you can think of these two criteria as penalizing models with many parameters (p in the case of linear regression). -

Cross-Validation for Selecting a Model Selection Procedure 1 Introduction
Cross-Validation for Selecting a Model Selection Procedure∗ Yongli Zhang Yuhong Yang LundQuist College of Business School of Statistics University of Oregon University of Minnesota Eugene, OR 97403 Minneapolis, MN 55455 Abstract While there are various model selection methods, an unanswered but important question is how to select one of them for data at hand. The difficulty is due to that the targeted behaviors of the model selection procedures depend heavily on uncheckable or difficult-to-check assumptions on the data generating process. Fortunately, cross- validation (CV) provides a general tool to solve this problem. In this work, results are provided on how to apply CV to consistently choose the best method, yielding new insights and guidance for potentially vast amount of application. In addition, we address several seemingly widely spread misconceptions on CV. Key words: Cross-validation, cross-validation paradox, data splitting ratio, adaptive procedure selection, information criterion, LASSO, MCP, SCAD 1 Introduction Model selection is an indispensable step in the process of developing a functional prediction model or a model for understanding the data generating mechanism. While thousands of papers have been published on model selection, an important and largely unanswered question is: How do we select a modeling procedure that typically involves model selection and parameter estimation? In a real application, one usually does not know which procedure fits the data the best. Instead of staunchly following one's favorite procedure, a better idea is to adaptively choose a modeling procedure. In 1 this article we focus on selecting a modeling procedure in the regression context through cross- validation when, for example, it is unknown whether the true model is finite or infinite dimensional in classical setting or if the true regression function is a sparse linear function or a sparse additive function in high dimensional setting. -

Lecture 6: Multiple Linear Regression
Lecture 6: Multiple linear regression c Christopher S. Bretherton Winter 2014 A natural extension is to regress a predictand y on multiple predictor vari- ables xm. Assuming all variables have been de-meaned, we fit the linear model: y^ = a1x1 + a2x2 ::: + aM xM : (6.0.1) 6.1 Mathematical derivation Least squares minimization of the mean square residual N N −1 X 2 −1 X 2 Q(a) = N [yj − y^j] = N [yj − (a1x1 ::: + aM xM )j] j=1 j=1 with respect to each coefficient ak gives the normal equations: a1x1x1 + a2x1x2 ::: + aM x1xM = x1y a2x2x1 + a2x2x2 ::: + aM x2xM = x2y . aM xM x1 + a2xM x2 ::: + aM xM xM = xM y The coefficients xixp are just the elements Cip of the M×M covariance matrix Cxx between the predictor variables, and the right-hand side is a column vector or M × 1 matrix of covariances between the predictors and the predictand, so the normal equation takes the matrix form: Cxxa = Cxy (6.1.1) The covariance matrices can be written directly in terms of the M ×N predictor matrix X (whose rows are the time series of the predictors) and the 1 × N predictand matrix Y (a row vector): 1 C = XXT xx N − 1 1 C = XYT (6.1.2) xy N − 1 1 Amath 482/582 Lecture 6 Bretherton - Winter 2014 2 As with simple linear regression, it is straightforward to apply multiple re- gression to a whole array of predictands. since the regression is computed sep- arately for each predictand variable. 6.2 Matlab example The Matlab script regression example.m was introduced in the previous lec- ture. -
Techniques, Stepwise Regression, Analysis of Covariance, Influence Measures, Computing Packages
POSSIBLE DESIGN AND STATISTICS COURSE FOR GGNB STUDENTS STATS 100 Applied Stats for Biomedical Science: Descriptive statistics, probability, sampling distributions, estimation, hypothesis testing, contingency tables, ANOVA, regression; implementation of statistical methods using computer package. STATS 102 Intro Probability Modeling and Statistical Inference: Rigorous precalculus introduction to probability and parametric/nonparametric statistical inference with computing; binomial, Poisson, geometric, normal, and sampling distributions; exploratory data analysis; regression analysis; ANOVA. STATS 106 Applied Statistical Methods – Analysis of Variance: One-way and two-way fixed effects analysis of variance models. Randomized complete and incomplete block design, Latin squares. Multiple comparisons procedures. One-way random effects model. STATS 108 Applied Statistical Methods: Regression Analysis: Simple linear regression, variable selection techniques, stepwise regression, analysis of covariance, influence measures, computing packages. STAT 130A Mathematical Statistics: Brief Course: Basic probability, densities and distributions, mean, variance, covariance, Chebyshev's inequality, some special distributions, sampling distributions, central limit theorem and law of large numbers, point estimation, some methods of estimation, interval estimation, confidence intervals for certain quantities, computing sample sizes. STAT 130B Mathematical Statistics: Brief Course: Transformed random variables, large sample properties of estimates. Basic