Portfolio Construction by Using Different Risk Models
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

December 2011 2Nd Quarter
growth through energy THE HUB POWER COMPANY LIMITED UNAUDITED QUARTERLY FINANCIAL STATEMENTS FOR THE SECOND QUARTER / HALF YEAR ENDED DECEMBER 31, 2011 Vision To be an energy leader – committed to deliver growth through energy. Mission To be a dynamic and growth – oriented energy company that achieves the highest international standards in its operations and delivers a fair return to its shareholders, while serving the community as a caring corporate citizen. C O N T E N T S THE HUB POWER COMPANY LIMITED PAGE Company Information 1 Report of the Directors 3 Auditors’ Review Report to the Members 5 Condensed Interim Unconsolidated Profit & Loss Account 7 Condensed Interim Unconsolidated Statement of 8 Comprehensive Income Condensed Interim Unconsolidated Balance Sheet 9 Condensed Interim Unconsolidated Cash Flow Statement 10 Condensed Interim Unconsolidated Statement of Changes in Equity. 11 Notes to the Condensed Interim Unconsolidated Financial Statements 12 THE HUB POWER COMPANY LIMITED and its Subsidiary Company Report of the Directors on the Consolidated Financial Statements 17 Condensed Interim Consolidated Profit & Loss Account 18 Condensed Interim Consolidated Statement of Comprehensive Income 19 Condensed Interim Consolidated Balance Sheet 20 Condensed Interim Consolidated Cash Flow Statement 21 Condensed Interim Consolidated Statement of Changes in Equity 22 Notes to the Condensed Interim Consolidated Financial Statements 23 COMPANY INFORMATION BOARD OF DIRECTORS M. A. Alireza H.I. (Chairman) Zafar Iqbal Sobani (Chief Executive) Dr. Fereydoon Abtahi Yousuf A. Alireza Robin A. Bramley Dr. Asif A. Brohi NBP Nominee Malcolm P. Clampin Taufique Habib Arshad A. Hashmi Qaiser Javed Iqbal Ahmed Khosa GOB Nominee Ali Munir Philippe F. -

The Hub Power Company Limited 2
The Pakistan Credit Rating Agency Limited Rating Report Report Contents 1. Rating Analysis The Hub Power Company Limited 2. Financial Information 3. Rating Scale 4. Regulatory and Supplementary Disclosure Rating History Dissemination Date Long Term Rating Short Term Rating Outlook Action Rating Watch 21-Jun-2021 AA+ A1+ Stable Maintain - 29-Jun-2020 AA+ A1+ Stable Maintain - 27-Dec-2019 AA+ A1+ Stable Maintain - 27-Jun-2019 AA+ A1+ Stable Maintain - 27-Dec-2018 AA+ A1+ Stable Maintain - 29-Jun-2018 AA+ A1+ Stable Maintain - 22-Dec-2017 AA+ A1+ Stable Maintain - 20-Apr-2017 AA+ A1+ Stable Maintain - 20-Apr-2016 AA+ A1+ Stable Maintain - 29-Jun-2015 AA+ A1+ Stable Maintain - Rating Rationale and Key Rating Drivers The rating reflects the holding company character of Hubco with an exclusive focus on the different dimension of the energy sector. In addition to the investment book, Hubco itself is a large RFO based power plant. Hubco aims to expand generation capacity to boost the country's power generation by utilizing Pakistan's indigenous natural resources. Hubco is setting up two coal power plants (i) Thar Energy Limited (TEL): 330MW and (ii) Thalnova Power: 330MW, mine-mouth coal-fired power plants at Thar. Hubco also has an investment in Sindh Engro Coal Mining Company (SECMC) and China Power Hub Generation Co (CPHGC). Moving forward, Hubco is looking to explore growth opportunities in diversified areas including water desalination, renewable energy, upstream oil & gas, mining and infrastructure. Through Hub Power Holdings Ltd, a wholly owned subsidiary of Hubco, entered in JV agreement (50:50) with ENI, Pakistan’s employees to form Prime Int. -

FACTSHEET - AS of 01-Oct-2021 Solactive GBS Pakistan Large & Mid Cap USD Index PR
FACTSHEET - AS OF 01-Oct-2021 Solactive GBS Pakistan Large & Mid Cap USD Index PR DESCRIPTION The Solactive GBS Pakistan Large & Mid Cap USD Index PR is part of the Solactive Global Benchmark Series which includes benchmark indices for developed and emerging market countries. The index intends to track the performance of the large and mid cap segment covering approximately the largest 85% of the free-float market capitalization in the Pakistani market. It is calculated as a pricereturn index in USD and weighted by free-float market capitalization. HISTORICAL PERFORMANCE 1,200 1,000 800 600 400 200 Jan-2008 Jan-2010 Jan-2012 Jan-2014 Jan-2016 Jan-2018 Jan-2020 Jan-2022 Solactive GBS Pakistan Large & Mid Cap USD Index PR CHARACTERISTICS ISIN / WKN DE000SLA8Y15 / SLA8Y1 Base Value / Base Date 1139 Points / 08.05.2006 Bloomberg / Reuters / .SPKLMCUP Last Price 347.48 Index Calculator Solactive AG Dividends Not included Index Type Price Return Calculation 8:00 am to 10:30 pm (CET), every 15 seconds Index Currency USD History Available daily back to 08.05.2006 Index Members 13 FACTSHEET - AS OF 01-Oct-2021 Solactive GBS Pakistan Large & Mid Cap USD Index PR STATISTICS 30D 90D 180D 360D YTD Since Inception Performance -11.24% -18.75% -20.18% -6.01% -14.20% -69.49% Performance (p.a.) - - - - - -7.42% Volatility (p.a.) 17.33% 14.90% 15.54% 17.78% 16.87% 23.20% High 391.47 429.41 459.90 459.90 459.90 1310.60 Low 343.18 343.18 343.18 343.18 343.18 250.61 Sharpe Ratio -4.42 -3.83 -2.37 -0.36 -1.11 -0.33 Max. -

Annual Report 2015
Annual Report 2015 The Way Forward At Bank Alfalah, we’ve never chosen the well-trodden path just because it’s the easiest option. We’ve always been different and defined our own rule of success. We are younger and more dynamic than the rest, and we’re drawn to people who share the same attitude. OUR WAY CUSTOMER CONNECT We want to inspire and help you find your own way in going after what you want, just as we have. We do all we can to understand and anticipate what will help you achieve your ambitions. LET’S INNOVATE We constantly question the status quo to find new and better ways to do things. With fresh eyes, we seek out new ways to meet your needs and help you shape your own path, through innovative products, insightful advice and a ‘can-do’ attitude. INSPIRING LEADERSHIP We foster leadership, inspiring employees and customers to do things differently and to succeed while delivering sustainable results. We inspire and recognise young, emerging talent in the country and provide them with opportunities to showcase their work. THE WAY FORWARD CONTENTS 01 Bank Alfalah Our Company 03 Vision, Mission and Values 04 Company Information 05 Directors’ Profile 07 Management Committee 11 Chairman’s Message 13 Directors’ Report 15 The Way Forward Customer Connect 27 Let’s Innovate 39 Inspiring Leadership 45 Corporate Information 51 Financial Information Financial Performance (Including Six Years Financial Summary) 63 Notice of the Annual General Meeting 73 Statement of Compliance with the Code of Corporate Governance (CCG) 75 Auditors’ Review -
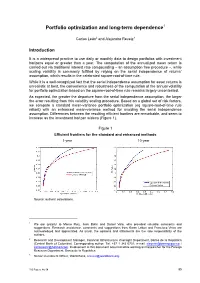
Portfolio Optimization and Long-Term Dependence1
Portfolio optimization and long-term dependence1 Carlos León2 and Alejandro Reveiz3 Introduction It is a widespread practice to use daily or monthly data to design portfolios with investment horizons equal or greater than a year. The computation of the annualized mean return is carried out via traditional interest rate compounding – an assumption free procedure –, while scaling volatility is commonly fulfilled by relying on the serial independence of returns’ assumption, which results in the celebrated square-root-of-time rule. While it is a well-recognized fact that the serial independence assumption for asset returns is unrealistic at best, the convenience and robustness of the computation of the annual volatility for portfolio optimization based on the square-root-of-time rule remains largely uncontested. As expected, the greater the departure from the serial independence assumption, the larger the error resulting from this volatility scaling procedure. Based on a global set of risk factors, we compare a standard mean-variance portfolio optimization (eg square-root-of-time rule reliant) with an enhanced mean-variance method for avoiding the serial independence assumption. Differences between the resulting efficient frontiers are remarkable, and seem to increase as the investment horizon widens (Figure 1). Figure 1 Efficient frontiers for the standard and enhanced methods 1-year 10-year Source: authors’ calculations. 1 We are grateful to Marco Ruíz, Jack Bohn and Daniel Vela, who provided valuable comments and suggestions. Research assistance, comments and suggestions from Karen Leiton and Francisco Vivas are acknowledged and appreciated. As usual, the opinions and statements are the sole responsibility of the authors. -

1. Syed Khalid Siraj Subhani 2. Mian Asad Hayaud
PROFILE OF CANDIDATES WHO HAVE FILED THEIR INTENTION TO OFFER THEMSELVES TO CONTEST IN THE ELECTION OF DIRECTORS AT THE 11th EXTRAORDINARY GENERAL MEETING SCHEDULED TO BE HELD ON MARCH 17, 2021. 1. Syed Khalid Siraj Subhani Mr. Subhani is a Chemical Engineer with Executive Management Program from Haas School of Business, University of California, Berkeley and Leadership program from MIT, Boston. A seasoned executive, his career spanned over 33 years with Exxon Chemical Pakistan Limited, which subsequently became Engro Chemical Pakistan Limited and later Engro Corporation Limited. This included long term assignments with Esso Chemical Canada in Edmonton and at ICI site in Billingham UK. Over the years, he worked in numerous senior executive positions at Engro and played instrumental role in growth and diversification of the company to make it one of the largest business conglomerates of Pakistan. Prior to retirement from Engro he worked as President and Chief Executive Officer of Engro Corporation Limited, Engro Fertilisers Limited and Engro Polymer and Chemicals Limited. Mr. Subhani also served as President and Chief Executive Officer of ThalNova Power Thar Private Limited for a period of two years. Earlier Mr. Subhani also served on the board of Engro Corporation Limited (Director), Hub Power Company Limited (Director), Engro Foods Limited (Director), Sindh Engro Coal Mining Company Limited (Director), Laraib Energy Limited (Director), Engro Fertilisers Limited (Board Chairman), Engro Polymer and Chemicals Limited (Board Chairman), Engro Vopak Terminal Limited (Board Chairman), Thar Power Company Limited (Board Chairman), Engro Powergen Qadirpur Limited (Board Chairman), Engro Elengy Terminal (Private) Limited (Board Chairman) and Engro Eximp Agri Products (Private) Limited (Board Chairman). -

Global Global Securities Pakistan Limited Draft Offer for Sale of Shares
INVESTORS ARE STRONGLY ADVISED IN THEIR OWN INTEREST TO CAREFULLY READ THE CONTENTS OF THE OFFER FOR SALE DOCUMENT, ESPECIALLY THE RISK FACTORS HIGHLIGHTED IN PARA 4.12, BEFORE MAKING ANY INVESTMENT DECISION OFFER FOR SALE OF 88,025,000 SHARES OF KOT ADDU POWER COMPANY LIMITED At an Offer Price of PKR 30/- per share (Including Premium of PKR 20/- per share) By Privatisation Commission, Government of Pakistan On behalf of Pakistan Water and Power Development Authority Public Subscription From xxx, 2005 to xxx, 2005 Date of Publication of this Offer for Sale Document is xxx, 2005 THIS IS NOT A PROSPECTUS BY KOT ADDU POWER COMPANY LIMITED (THE COMPANY) BUT AN OFFER FOR SALE BY THE PRIVATISATION COMMISSION, GOVERNMENT OF PAKISTAN ON BEHALF OF WAPDA (THE OFFERER) OUT OF WAPDA’S SHAREHOLDING IN THE COMPANY Lead Manager to the Offer Global Global Securities Pakistan Limited Draft Offer for Sale of Shares GLOSSARY OF TECHNICAL TERMS AND ABBREVIATIONS 2 CDA Central Depository Act,1997 CDC The Central Depository Company of Pakistan Limited CDS Central Depository System CEGB Central Electricity DraftGenerating Board, UK Offer for Sale of Shares Company Kot Addu Power Company Limited CPP Capacity Purchase Price, means an element of tariff payable by WAPDA to KAPCO as defined in the “Power Purchase Agreement” DISCOs Distribution Companies EPP Energy Purchase Price, means an element of tariff payable by WAPDA to KAPCO as defined in the “Power Purchase Agreement” Escalable Means indexed to the US Consumer Price Index and Rupee-US Dollar Exchange Rate -

Download 309.24 KB
ASIAN DEVELOPMENT BANK RRP: PAK 32146 REPORT AND RECOMMENDATION OF THE PRESIDENT TO THE BOARD OF DIRECTORS ON PROPOSED LOANS TO THE ISLAMIC REPUBLIC OF PAKISTAN FOR THE ENERGY SECTOR RESTRUCTURING PROGRAM November 2000 CURRENCY EQUIVALENTS (as of 15 November 2000) Currency Unit − Pakistan Rupee (PRe/PRs) PRe1.00 = $0.0178 $1.00 = PRs56.25 Pakistan maintains a managed floating rate system under which the rupee is fixed on a daily basis in terms of the US dollar. ABBREVIATIONS ADB − Asian Development Bank ATM − automated teller machine DISCO − distribution company ESAF − Enhanced Structural Adjustment Facility FAC − fuel adjustment charges FATA − federally administered tribal areas GDP − gross domestic product GENCO − generation company HUBCO − Hub Power Company IMF − International Monetary Fund IPP − independent power producer KAPCO − Kot Addu Power Company KESC − Karachi Electric Supply Corporation LPG − liquefied petroleum gas MOF − Ministry of Finance and Economic Affairs NEPRA − National Electric Power Regulatory Authority NTDC − National Transmission and Dispatch Company PEPCO − Pakistan Electric Power Company PRGF − poverty reduction growth facility SAL − structural adjustment loan SNGPL − Sui Northern Gas Pipeline Company Limited SOE − State-owned enterprise SSGC − Sui Southern Gas Pipeline Company TA − technical assistance T&D − transmission and distribution WAPDA − Water and Power Development Authority WEIGHTS AND MEASURES GWh - gigawatt-hour (1,000 megawatt-hours) km - kilometer kV - Kilovolt (1,000 volt) kWh - kilowatt-hour (1,000 watt-hours) mmcfd - million cubic feet per day MW - megawatt (1,000 kilowatts) NOTES (i) The fiscal year (FY) of the Government ends on 30 June. FY before a calendar year denotes the year in which the FY ends. -

Habibmetro Modaraba Management (AN(AN ISLAMICISLAMIC FINANCIALFINANCIAL INSTITUTION)INSTITUTION)
A N N U A L R E P O R T 2017 1 HabibMetro Modaraba Management (AN(AN ISLAMICISLAMIC FINANCIALFINANCIAL INSTITUTION)INSTITUTION) 2 A N N U A L R E P O R T 2017 JOURNEY OF CONTINUOUS SUCCESS A long term partnership Over the years, First Habib Modaraba (FHM) has become the sound, strong and leading Modaraba within the Modaraba sector. Our stable financial performance and market positions of our businesses have placed us well to deliver sustainable growth and continuous return to our investors since inception. During successful business operation of more than 3 decades, FHM had undergone with various up and down and successfully countered with several economic & business challenges. Ever- changing requirement of business, product innovation and development were effectively managed and delivered at entire satisfaction of all stakeholders with steady growth on sound footing. Consistency in perfect sharing of profits among the certificate holders along with increase in certificate holders' equity has made FHM a sound and well performing Modaraba within the sector. Our long term success is built on a firm foundation of commitment. FHM's financial strength, risk management protocols, governance framework and performance aspirations are directly attributable to a discipline that regularly brings prosperity to our partners and gives strength to our business model which is based on true partnership. Conquering with the challenges of our operating landscape, we have successfully journeyed steadily and progressively, delivering consistent results. With the blessing of Allah (SWT), we are today the leading Modaraba within the Modaraba sector of Pakistan, demonstrating our strength, financial soundness and commitment in every aspect of our business. -

Financial Page 2016
Other Matters We would like to draw your attention to the ■ There are no significant doubts upon the following notes in the financial statements which Associated Companies Corporate and Financial Company’s ability to continue as a going concern. contain the information and explanations to Reporting Framework matters highlighted by External Auditors in their Asia Petroleum Limited (APL) ■ There has been no material departure from the best practices of corporate governance, as Audit Report: PSO’s Board is fully cognizant of its responsibility APL was incorporated in Pakistan as an unlisted detailed in the listing regulations and Public public limited company on July 17, 1994. The as recognized by Code of Corporate Governance, ■ Note 12.2 – Non provisioning of past due Sector Code of Corporate Governance. Company has been principally established to detailed in listing regulation and Public Sector receivable from Power Generation Companies Companies (Corporate Governance) Rules, 2013 transport “Residual Fuel Oil” (RFO) to the Hub ■ Key operating and financial data of last six years aggregating to Rs. 101,407 million (net of issued by Securities & Exchange Commission of Power Company Limited (HUBCO) at Hub, in a summarized form is annexed. provision of Rs. 532 million); inclusive of Pakistan (SECP). Rs.11,890 million received subsequent to the Balochistan. For this purpose, the Company laid an underground oil pipeline starting from Pakistan ■ The following is the value of investment of balance sheet date. Following are the comments on acknowledgement State Oil Company Limited’s (PSO) Zulfiqarabad provident and pension funds based on their of PSO’s commitment towards high standards of terminal at Pipri to HUBCO at Hub. -

Annual Report 2020
BRINGING LIGHT FOR A NEW LIFE Throughout time, HUBCO has mustered an extraordinary array of resources – from groundbreaking research to diligent Human Resource. Like the rising sun, HUBCO shines bright and continues to enlighten lives. Our destiny – to bring change, new life and zest to our great Nation through our continued efforts. CONTENTS 05 05 06 07 08 09 Vision & Mission Core Values Company Profile Group Structure Business Strategy SWOT Analysis 10 12 14 20 22 23 Company Geographical Board & Leadership Board & Functional Management Team Organizational Information Presence Committees Structure 24 26 28 30 45 46 A Brief History of Chairman’s Review CEO’s Message Report of the Report of the Review Report to the HUBCO Directors Directors (Urdu) Members 47 49 50 51 54 66 Statement of Awards & Calendar of Calendar of Corporate Social Corporate Compliance Achievements Corporate Events Major Events Responsibility Governance Financial Performance 72 73 74 76 78 80 Financial Ratio Dupont Analysis Horizontal and Horizontal Analysis Vertical Analysis of Six Years Statement Vertical Analysis of of Statement Statement of of Profit or Loss at a Statement of Profit of Financial Position Financial Position Glance or Loss 81 82 83 84 85 86 Six Years Statement Summary of Six Statement of Value Quarterly Financial Statement of Cash Graphical of Financial Position Years Cash Flow Addition Analysis Flow - Direct Method Presentation at a Glance at a Glance BRINGING LIGHT 20 2 FOR A NEW LIFE ANNUAL REPORT 20 Unconsolidated Financial Statements 91 96 97 -

BANK ALFALAH LIMITED 02 Corporate Information
In the Name Of Allah The Most Gracious, The Most Merciful 01 Contents Corporate Information ...............................................................................2 Notice of the 14th Annual General Meeting.................................................3 Directors’ Report to the Shareholders ........................................................5 Statement of Compliance with the Best Practices of Corporate Governance to the Members..................................................9 Review Report to the Members on Statement of Compliance with Best Practices of Code of Corporate Governance..............................11 Statement of Internal Controls .................................................................12 Auditors’ Report to the Members.............................................................13 Balance Sheet.........................................................................................14 Profit and Loss Account ..........................................................................15 Cash Flow Statement ..............................................................................16 Statement of Changes in Equity ...............................................................17 Notes to the Financial Statements............................................................18 Consolidated Annual Accounts of Bank and its Subsidiary Companies......57 Pattern of Shareholding .........................................................................103 Branch Network ....................................................................................107