DOCSLIB.ORG

On the Origin of the Word ``Ellipse''

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
On the Origin of the Word ``Ellipse'' On the origin of the word \ellipse" Jan P. Hogendijk Department of Mathematics, University of Utrecht, Netherlands 2017 Ancient Greek mathematics. Period: 550 BC - ca. 250 CE Area: Greece, Southern Italy, Western Turkey, Egypt. Ancient Greek words that we still use. \Mathematics" = ta math`emata,the things that can be learned axiom, theorem, lemma asymptote, hyperbola, ellipse, parabola The basic work: the Elements by Euclid of Alexandria (ca 300 BC). Axioms, definitions, proofs. High theoretical level. Written originally on papyrus, medieval copies on parchment. Activity of Greek citizens in their free time (\schole"). Elements, 10th century CE manuscript of parchment (> 10 sheep necessary). Euclid's theory of ratios (which also works for irrational ratios) in \Book 5" of the Elements. Book 5, Definition 4 Logon echein pros all`elamegeth`elegetai ha dunantai pollaplasiazomena all`el¯onhuperechein. Book 5, Definition 5 En t¯oiaut¯oilog¯oimegeth`elegetai einai pr¯otonpros deuteron kai triton pros tetarton hotan ta tou pr¯otou kai tritou isakis pollaplasia t¯ontou deuterou kai tetartou isakis pollaplasi¯onkath' hopoionoun pollaplasiasmon hekateron hekateron `ehama huperech`ei`ehama isa `ehama elleip`eil`efthentakatall`ela Euclid's Greek text (tr. Heath) Def. 4 \Magnitudes are said to have a ratio to one another which are capable, when multiplied, of exceeding one another." Def. 5 \Magnitudes are said to be in the same ratio, the first to the second and the third to the fourth, when, if equimultiples be taken of the first and third, and equimultiples of the second and fourth, whatever equimultiples they are, then the former equimultiples alike exceed, are alike equal to, or alike fall short of the latter equimultiples respectively taken in corresponding order." Def. 5 A : B = C : D if for any integers m; n mA > nB ! mC > nD mA = nB ! mC = nD and mA < nB ! mC < nD Theorem: if A : B = C : D and C : D = E : F then A : B = E : F . (Proposition 11 of Book 5). In modern notation In modern terms: Def. 4. A and B can have a ratio if there are integers m; n such that mA > B and nB > A. In modern notation In modern terms: Def. 4. A and B can have a ratio if there are integers m; n such that mA > B and nB > A. Def. 5 A : B = C : D if for any integers m; n mA > nB ! mC > nD mA = nB ! mC = nD and mA < nB ! mC < nD Theorem: if A : B = C : D and C : D = E : F then A : B = E : F . (Proposition 11 of Book 5). The ellipse Term ellipse introduced by Apollonius of Perga (Western Turkey, 200 BC) in his work Conics The Conics consists of 8 Books, of which 4 have been preserved in Greek, books 5-7 in Arabic only. Book 8 is lost. It is assumed that the reader knows (most of) Euclid's Elements. The exposition follows a strict ritual. Example of text and translation: Conics I:13, Greek A E Λ P Π M O ∆ ΘΞ N Z B Γ H K Example of text and translation: Conics I:13, Greek. If a cone is cut by a plane through the axis, and by another plane meeting each side of the axial triangle, being neither parallel to the base nor subcontrary, and let the plane containing the base of the cone meet the cutting plane in a straight line perpendicular either to the base of the axial triangle or to its rectilinear extension; then any parallel line drawn from the section of the cone (parallel) to the common section of the planes as far as the diameter of the section will be equal in square to a certain area applied to a certain straight line, such that the diameter of the section will bear to it the same ratio as the square on the line drawn from the vertex of the cone parallel to the diameter of the section as far as the base of the triangle bears to the rectangle contained by the intercepts made by it on the sides of the triangle; the (area) having (as its) breadth the intercept made by it on the diameter in the direction of the vertex of the section, and being deficient (Greek: elleipon) by a figure similar and similarly situated to the rectangle contained by the diameter and the line along which they are equal in square; and let such a section be called an ellipse. Step 2: the same in notation (see handout p. 319, taken from Greek Mathematical Works, tr. Ivor Thomas, vol. 2). To understand this, note: I conic section is intersection of oblique cone with a plane. An oblique cone has a circular base and a vertex not in the base plane. I A \diameter" of a conic section with the correspondiung \ordinates" are defined in the definitions, see handout p. 287. (This is related to, but not the same as, a modern coordinate system) I every conic section has (at least) one diameter, proved in Prop. 7, handout pp. 289-295. I \subcontrary" section is the intersection of a cone with a plane not parallel to the base, which section nevertheless produces a circle. Name \ellipse" is related to its \equation": T1T2 diameter of the ellipse, QR an arbitrary ordinate. Put T1T2 = d; T1R = x, QR = y. There is a constant segment p = T1U1 perpendicular to T1T2 such that 2 p 2 y = px − d x = T1RVW , the rectangle along p = T1U1 with side x = T1R, which falls short by a rectangle WVSU1 similar to T1T2U2U1. Exercise can be of two levels. Level 1: Try to understand Conics book 1, proposition 13 (Ellipse). Write a clear account of what Apollonius tries to do, you can use modern notation. Level 2: Try to understand the transition to a new diameter, Conics book 1, proposition 50 (handout pp. 328 and further), but only for the ellipse. Write a clear account of what Apollonius tries to do, you can use modern notation. You can use any literature you like! Level 2 is only for those of you who want hard math. This presentation can be downloaded at http://www.jphogendijk.nl/talks/ellipse.pdf.
Load more

Recommended publications
  • Section 3.7 Notes
    Section 3.7 Notes Rational Functions 1 Introduction Definition • A rational function is fraction of two polynomials. 2x2 − 1 • For example, f(x) = is a rational function. 3x2 + 2x − 5 Properties of Rational Graphs • The graph of every rational function is smooth (no sharp corners) • However, many rational functions are discontinuous . In other words, the graph might have several separate \sections" to the graph, similar to the way piecewise functions look. 1 For example, remember the graph of f(x) = x : Notice how the graph is drawn in two separate pieces. Asymptotes • An asymptote to a function is a line which the function gets closer and closer to without touching. • Rational functions have two categories of asymptote: 1. vertical asymptotes 2. asymptotes which determine the end behavior - these could be either horizontal asymp- totes or slant asymptotes Vertical Asymptote Horizontal Slant Asymptote Asymptote 1 2 Vertical Asymptotes Description • A vertical asymptote of a rational function is a vertical line which the graph never crosses, but does get closer and closer to. • Rational functions can have any number of vertical asymptotes • The number of vertical asymptotes determines the number of \pieces" the graph has. Since the graph will never cross any vertical asymptotes, there will be separate pieces between and on the sides of all the vertical asymptotes. Finding Vertical Asymptotes 1. Factor the denominator. 2. Set each factor equal to zero and solve. The locations of the vertical asymptotes are nothing more than the x-values where the function is undefined. Behavior Near Vertical Asymptotes The multiplicity of the vertical asymptote determines the behavior of the graph near the asymptote: Multiplicity Behavior even The two sides of the asymptote match - they both go up or both go down.
    [Show full text]
  • Vertical Tangents and Cusps
    Section 4.7 Lecture 15 Section 4.7 Vertical and Horizontal Asymptotes; Vertical Tangents and Cusps Jiwen He Department of Mathematics, University of Houston [email protected] math.uh.edu/∼jiwenhe/Math1431 Jiwen He, University of Houston Math 1431 – Section 24076, Lecture 15 October 21, 2008 1 / 34 Section 4.7 Test 2 Test 2: November 1-4 in CASA Loggin to CourseWare to reserve your time to take the exam. Jiwen He, University of Houston Math 1431 – Section 24076, Lecture 15 October 21, 2008 2 / 34 Section 4.7 Review for Test 2 Review for Test 2 by the College Success Program. Friday, October 24 2:30–3:30pm in the basement of the library by the C-site. Jiwen He, University of Houston Math 1431 – Section 24076, Lecture 15 October 21, 2008 3 / 34 Section 4.7 Grade Information 300 points determined by exams 1, 2 and 3 100 points determined by lab work, written quizzes, homework, daily grades and online quizzes. 200 points determined by the final exam 600 points total Jiwen He, University of Houston Math 1431 – Section 24076, Lecture 15 October 21, 2008 4 / 34 Section 4.7 More Grade Information 90% and above - A at least 80% and below 90%- B at least 70% and below 80% - C at least 60% and below 70% - D below 60% - F Jiwen He, University of Houston Math 1431 – Section 24076, Lecture 15 October 21, 2008 5 / 34 Section 4.7 Online Quizzes Online Quizzes are available on CourseWare. If you fail to reach 70% during three weeks of the semester, I have the option to drop you from the course!!!.
    [Show full text]
  • Class 1: Overview of the Course; Ptolemaic Astronomy
    a. But marked variations within this pattern, and hence different loops from one occasion to another: e.g. 760 days one time, 775 another, etc. b. Planetary speeds vary too: e.g. roughly 40 percent variation in apparent longitudinal motion per day of Mars from one extreme to another while away from retrograde 4. Each of the five planets has its own distinct basic pattern of periods of retrograde motion, and its own distinct pattern of variations on this basic pattern a. Can be seen in examples of Mars and Jupiter, where loops vary b. An anomaly on top of the anomaly of retrograde motion c. Well before 300 B.C. the Babylonians had discovered “great cycles” in which the patterns of retrograde loops and timings of stationary points repeat: e.g. 71 years for Jupiter (see Appendix for others) 5. The problem of the planets: give an account ('logos') of retrograde motion, including basic pattern, size of loops, and variations for each of the five planets a. Not to predict longitude and latitude every day b. Focus instead on salient events – i.e. phenomena: conjunctions, oppositions, stationary points, longitudinal distance between them c. For the Babylonians, just predict; for the Greeks, to give a geometric representation of the constituent motions giving rise to the patterns 6. Classical designations: "the first inequality": variation in mean daily angular speed, as in 40 percent variation for Mars and smaller variation for Sun; "the second inequality": retrograde motion, as exhibited by the planets, but not the sun and moon D. Classical Greek Solutions 1.
    [Show full text]
  • Calculus Terminology
    AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential
    [Show full text]
  • Hypatia of Alexandria
    Hypathia of Alexandria Doina Ionescu Astronomical Institute of the Romanian Academy, E–mail: [email protected] Introduction - Born in 350-355/370; - Lived and learned in Alexandria, Roman Egypt; - The daughter of Theon, the last director of the Museum of Alexandria; - Trained by her father in physical education, mathematics, astronomy, philosophy, arts, literature, the principles of teaching, oratory; - Died in 415, killed by a Christian mob who blamed her for religious turmoil. The Musaeum of Alexandria - Founded in the 3rd century BCE by Ptolemy I Soter or his son Ptolemy II; - Comprised gardens, a room for shared dining, a reading room, lecture halls, meetings rooms and a library; - The Library of Alexandria: an acquisitions department and a cataloguing department; - The Mouseion (“The House of the Muses”) – an institution that brought together the best scholars of the Hellenistic world, a university; - Destruction of the Mouseion and Library of Alexandria: 1. Julius Caesar’s Fire in the Alexandrian War, 48 BC; 2. The attack of Aurelian in the 3rd century AD; 3. The decree of Theophilus in AD 391; 4. The Muslim conquest in AD 642 and thereafter. Theon (b: 335 – d. early 5th century) - Most of the references on him and on Hypathia : Suda, the 10th century Byzantine encyclopedia; - Highly educated scholar, mathematician and astronomer; - A member and possibly the last director of the Alexandrian Museion, on public payroll. - Devoted his scholarship to the study of his predecessors Euclid and Ptolemy; his recensions were designed for students; - Euclid’s Elements; - Thirteen books of Ptolemy’ Almagest ; Handy Tables : The Great Commentary, in five books, and The Little Commentary , in one; - He worked together with scholar and student associates and with his daughter, Hypathia - A treatise “On the Small Astrolabe” ; - On Signs and the examination of Birds and the Croaking of Ravens: two essays on the function of the star Syrius and the influence of the planetary spheres on the Nile; - 364 AD: predicted eclipses of the Sun and Moon in Alexandria.
    [Show full text]
  • Apollonius of Pergaconics. Books One - Seven
    APOLLONIUS OF PERGACONICS. BOOKS ONE - SEVEN INTRODUCTION A. Apollonius at Perga Apollonius was born at Perga (Περγα) on the Southern coast of Asia Mi- nor, near the modern Turkish city of Bursa. Little is known about his life before he arrived in Alexandria, where he studied. Certain information about Apollonius’ life in Asia Minor can be obtained from his preface to Book 2 of Conics. The name “Apollonius”(Apollonius) means “devoted to Apollo”, similarly to “Artemius” or “Demetrius” meaning “devoted to Artemis or Demeter”. In the mentioned preface Apollonius writes to Eudemus of Pergamum that he sends him one of the books of Conics via his son also named Apollonius. The coincidence shows that this name was traditional in the family, and in all prob- ability Apollonius’ ancestors were priests of Apollo. Asia Minor during many centuries was for Indo-European tribes a bridge to Europe from their pre-fatherland south of the Caspian Sea. The Indo-European nation living in Asia Minor in 2nd and the beginning of the 1st millennia B.C. was usually called Hittites. Hittites are mentioned in the Bible and in Egyptian papyri. A military leader serving under the Biblical king David was the Hittite Uriah. His wife Bath- sheba, after his death, became the wife of king David and the mother of king Solomon. Hittites had a cuneiform writing analogous to the Babylonian one and hi- eroglyphs analogous to Egyptian ones. The Czech historian Bedrich Hrozny (1879-1952) who has deciphered Hittite cuneiform writing had established that the Hittite language belonged to the Western group of Indo-European languages [Hro].
    [Show full text]
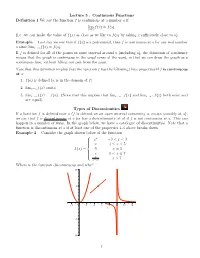
  • Lecture 5 : Continuous Functions Definition 1 We Say the Function F Is
    Lecture 5 : Continuous Functions Definition 1 We say the function f is continuous at a number a if lim f(x) = f(a): x!a (i.e. we can make the value of f(x) as close as we like to f(a) by taking x sufficiently close to a). Example Last day we saw that if f(x) is a polynomial, then f is continuous at a for any real number a since limx!a f(x) = f(a). If f is defined for all of the points in some interval around a (including a), the definition of continuity means that the graph is continuous in the usual sense of the word, in that we can draw the graph as a continuous line, without lifting our pen from the page. Note that this definition implies that the function f has the following three properties if f is continuous at a: 1. f(a) is defined (a is in the domain of f). 2. limx!a f(x) exists. 3. limx!a f(x) = f(a). (Note that this implies that limx!a− f(x) and limx!a+ f(x) both exist and are equal). Types of Discontinuities If a function f is defined near a (f is defined on an open interval containing a, except possibly at a), we say that f is discontinuous at a (or has a discontinuiuty at a) if f is not continuous at a. This can happen in a number of ways. In the graph below, we have a catalogue of discontinuities. Note that a function is discontinuous at a if at least one of the properties 1-3 above breaks down.
    [Show full text]
  • A Modern Almagest an Updated Version of Ptolemy’S Model of the Solar System
    A Modern Almagest An Updated Version of Ptolemy’s Model of the Solar System Richard Fitzpatrick Professor of Physics The University of Texas at Austin Contents 1 Introduction 5 1.1 Euclid’sElementsandPtolemy’sAlmagest . ......... 5 1.2 Ptolemy’sModeloftheSolarSystem . ..... 5 1.3 Copernicus’sModeloftheSolarSystem . ....... 10 1.4 Kepler’sModeloftheSolarSystem . ..... 11 1.5 PurposeofTreatise .................................. .. 12 2 Spherical Astronomy 15 2.1 CelestialSphere................................... ... 15 2.2 CelestialMotions ................................. .... 15 2.3 CelestialCoordinates .............................. ..... 15 2.4 EclipticCircle .................................... ... 17 2.5 EclipticCoordinates............................... ..... 18 2.6 SignsoftheZodiac ................................. ... 19 2.7 Ecliptic Declinations and Right Ascenesions. ........... 20 2.8 LocalHorizonandMeridian ............................ ... 20 2.9 HorizontalCoordinates.............................. .... 23 2.10 MeridianTransits .................................. ... 24 2.11 Principal Terrestrial Latitude Circles . ......... 25 2.12 EquinoxesandSolstices. ....... 25 2.13 TerrestrialClimes .................................. ... 26 2.14 EclipticAscensions .............................. ...... 27 2.15 AzimuthofEclipticAscensionPoint . .......... 29 2.16 EclipticAltitudeandOrientation. .......... 30 3 Dates 63 3.1 Introduction...................................... .. 63 3.2 Determination of Julian Day Numbers . .... 63 4 Geometric
    [Show full text]
  • Hypatia of Alexandria Anne Serban
    Hypatia of Alexandria Anne Serban Hypatia's Life Hypatia of Alexandria was born sometime between the years 350 to 370 AD in Alexandria of Egypt. She was the only daughter of Theon of Alexandria; no information exists about her mother. "Hypatia may have had a brother, Epiphanius, though he may have been only Theon's favorite pupil." Theon did not want to force his daughter to become the typical woman described by historian Slatkin when he wrote "Greek women of all classes were occupied with the same type of work, mostly centered around the domestic needs of the family. Women cared for young children, nursed the sick, and prepared food." Instead he educated her in math, astronomy and philosophy, as well as in different religions. Theons desire that his daughter be different from the mold that society created for women influenced the rest of Hypatias life. Eventually Hypatia became a teacher herself. She instructed her pupils, who were both pagans and Christians, in math, astronomy, and philosophy, focusing mostly on Neoplatonism. She also held lectures on various topics, often drawing many eager listeners. Her greatest contributions benefitted the fields of mathematics and astronomy. By 400 AD, she became the head of the Platonist school in Alexandria. "Hypatia, on the other hand, led the life of a respected academic at Alexandria's university; a position to which, as far as the evidence suggests, only males were entitled previously." Hypatia took many of Platos ideas as personal applications, choosing even to live a life of celibacy. Furthermore, Hypatia wrote three commentaries and worked with Theon on several books.
    [Show full text]
  • GRAPH of a RATIONAL FUNCTION Find Vertical Asymptotes and Draw
    GRAPH OF A RATIONAL FUNCTION Find vertical asymptotes and draw them. Look for common factors first. Vertical asymptotes occur where the denominator becomes zero as long as there are no common factors. Find the horizontal asymptote, if any, and draw it. A horizontal asymptote may be found using the exponents and coefficients of the lead terms in the numerator and denominator. Please see “Horizontal Asymptotes and Lead Coefficients” below. Pick two or three x-values to the left and right of each vertical asymptote . If there are no vertical asymptotes, then just pick 2 positive, 2 negative, and zero. Put these values into the function f(x) and plot the points. This will give you an idea of the shape of the curve. You will quickly see whether the graph goes above or below the horizontal asymptote . Find the y-intercept by letting x = 0 . Put “0” into the function, do the arithmetic and get the y-value. Plot the point ( 0, y ). This will show you where the curve crosses the y-axis. Find any x-intercepts by letting y = 0 . Replace f(x) by “0”, then solve for x. Plot these points as (x, 0 ). This will show you where the graph crosses the x-axis. By the way, when you set y =0 it is possible that you will get imaginary answers for x. Since we can not graph a + bi on the “real plane”, this means there are no x-intercepts. Finally, connect all of the points (x, y ) with a smooth curve rather than choppy, straight line segments.
    [Show full text]
  • MATH 12002 - CALCULUS I §1.6: Horizontal Asymptotes
    MATH 12002 - CALCULUS I x1.6: Horizontal Asymptotes Professor Donald L. White Department of Mathematical Sciences Kent State University D.L. White (Kent State University) 1 / 5 Horizontal Asymptotes Horizontal asymptotes are very closely related to limits at infinity. Definition Let y = f (x) be a function and let L be a number. The line y = L is a horizontal asymptote of f if lim f (x) = L or lim f (x) = L: x!+1 x→−∞ Notes: The definition means that the graph of f is very close to the horizontal line y = L for large (positive or negative) values of x. A function can have at most two different horizontal asymptotes. A graph can approach a horizontal asymptote in many different ways; see Figure 8 in x1.6 of the text for graphical illustrations. In particular, a graph can, and often does, cross a horizontal asymptote. Let's emphasize this point to avoid problems later: D.L. White (Kent State University) 2 / 5 Horizontal Asymptotes THERE'S NO REASON | HERE'S MY POINT, DUDE | THERE'S NO #^|%!*& REASON WHY THE GRAPH OF A FUNCTION CAN'T CROSS A HORIZONTAL ASYMPTOTE!! D.L. White (Kent State University) 3 / 5 Horizontal Asymptotes Our general result on limits at infinity of rational functions implies the following. Theorem P(x) Let f (x) = Q(x) be a rational function (P(x),Q(x) are polynomials). If deg P(x) = deg Q(x), then the horizontal asymptote of f (x) is p y = ; q where p, q are the leading coefficients of P(x),Q(x), respectively.
    [Show full text]
  • Section 9.2 Hyperbolas 597
    Section 9.2 Hyperbolas 597 Section 9.2 Hyperbolas In the last section, we learned that planets have approximately elliptical orbits around the sun. When an object like a comet is moving quickly, it is able to escape the gravitational pull of the sun and follows a path with the shape of a hyperbola. Hyperbolas are curves that can help us find the location of a ship, describe the shape of cooling towers, or calibrate seismological equipment. The hyperbola is another type of conic section created by intersecting a plane with a double cone, as shown below5. The word “hyperbola” derives from a Greek word meaning “excess.” The English word “hyperbole” means exaggeration. We can think of a hyperbola as an excessive or exaggerated ellipse, one turned inside out. We defined an ellipse as the set of all points where the sum of the distances from that point to two fixed points is a constant. A hyperbola is the set of all points where the absolute value of the difference of the distances from the point to two fixed points is a constant. 5 Pbroks13 (https://commons.wikimedia.org/wiki/File:Conic_sections_with_plane.svg), “Conic sections with plane”, cropped to show only a hyperbola by L Michaels, CC BY 3.0 598 Chapter 9 Hyperbola Definition A hyperbola is the set of all points Q (x, y) for which the absolute value of the difference of the distances to two fixed points F1(x1, y1) and F2 (x2, y2 ) called the foci (plural for focus) is a constant k: d(Q, F1 )− d(Q, F2 ) = k .
    [Show full text]