Supplementary Data
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

PEX2 Is the E3 Ubiquitin Ligase Required for Pexophagy During Starvation
JCB: Article PEX2 is the E3 ubiquitin ligase required for pexophagy during starvation Graeme Sargent,1,6 Tim van Zutphen,7 Tatiana Shatseva,6 Ling Zhang,3 Valeria Di Giovanni,3 Robert Bandsma,2,3,4,5 and Peter Kijun Kim1,6 1Cell Biology Department, 2Department of Paediatric Laboratory Medicine, 3Physiology and Experimental Medicine Program, Research Institute, 4Division of Gastroenterology, Hepatology and Nutrition, and 5Centre for Global Child Health, The Hospital for Sick Children, Toronto, ON M5G 1X8, Canada 6Biochemistry Department, University of Toronto, Toronto, ON M5S 1A8, Canada 7Department of Pediatrics, Center for Liver, Digestive and Metabolic Diseases, University of Groningen, University Medical Center Groningen, 9700 AD Groningen, Netherlands Peroxisomes are metabolic organelles necessary for anabolic and catabolic lipid reactions whose numbers are highly dynamic based on the metabolic need of the cells. One mechanism to regulate peroxisome numbers is through an auto- phagic process called pexophagy. In mammalian cells, ubiquitination of peroxisomal membrane proteins signals pexo- phagy; however, the E3 ligase responsible for mediating ubiquitination is not known. Here, we report that the peroxisomal E3 ubiquitin ligase peroxin 2 (PEX2) is the causative agent for mammalian pexophagy. Expression of PEX2 leads to Downloaded from gross ubiquitination of peroxisomes and degradation of peroxisomes in an NBR1-dependent autophagic process. We identify PEX5 and PMP70 as substrates of PEX2 that are ubiquitinated during amino acid starvation. We also find that PEX2 expression is up-regulated during both amino acid starvation and rapamycin treatment, suggesting that the mTORC1 pathway regulates pexophagy by regulating PEX2 expression levels. Finally, we validate our findings in vivo using an animal model. -

HEXIM1 (D5Y5K) Rabbit
HEXIM1 (D5Y5K) Rabbit mAb Store at -20°C 3 n 100 µl Orders n 877-616-CELL (2355) (10 western blots) [email protected] Support n 877-678-TECH (8324) [email protected] Web n www.cellsignal.com rev. 01/05/15 #12604 For Research Use Only. Not For Use In Diagnostic Procedures. Entrez-Gene ID #10614 UniProt ID #O94992 Storage: Supplied in 10 mM sodium HEPES (pH 7.5), 150 Applications Species Cross-Reactivity* Molecular Wt. Isotype mM NaCl, 100 µg/ml BSA, 50% glycerol and less than 0.02% W, IP, IF-IC H, Mk 60 kDa Rabbit IgG** sodium azide. Store at –20°C. Do not aliquot the antibody. Endogenous *Species cross-reactivity is determined by western blot. Background: Hexamethylene bis-acetamide-inducible ** Anti-rabbit secondary antibodies must be used to protein 1 (HEXIM1) was originally identified in vascular kDa HeLa A-431 Hep G2 COS-7 detect this antibody. smooth muscle cells as a protein that is upregulated upon 200 Recommended Antibody Dilutions: treatment with the differentiating agent hexamethylene bi- 140 Western blotting 1:1000 sacetamide (1). HEXIM1 binds 7SK RNA, a highly abundant 100 Immunoprecipitation 1:100 non-coding RNA, and together they act as a potent inhibitor 80 Immunofluorescence (IF-IC) 1:1200 of positive transcription elongation factor b (P-TEFb) (2,3). 60 HEXIM1 P-TEFb phosphorylates the C-terminal domain of the largest 50 For product specific protocols please see the web page subunit of RNA polymerase II and is an important regulator for this product at www.cellsignal.com. 40 of transcription elongation (4-8). -
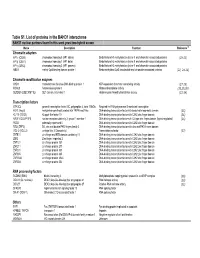
Table S1. List of Proteins in the BAHD1 Interactome
Table S1. List of proteins in the BAHD1 interactome BAHD1 nuclear partners found in this work yeast two-hybrid screen Name Description Function Reference (a) Chromatin adapters HP1α (CBX5) chromobox homolog 5 (HP1 alpha) Binds histone H3 methylated on lysine 9 and chromatin-associated proteins (20-23) HP1β (CBX1) chromobox homolog 1 (HP1 beta) Binds histone H3 methylated on lysine 9 and chromatin-associated proteins HP1γ (CBX3) chromobox homolog 3 (HP1 gamma) Binds histone H3 methylated on lysine 9 and chromatin-associated proteins MBD1 methyl-CpG binding domain protein 1 Binds methylated CpG dinucleotide and chromatin-associated proteins (22, 24-26) Chromatin modification enzymes CHD1 chromodomain helicase DNA binding protein 1 ATP-dependent chromatin remodeling activity (27-28) HDAC5 histone deacetylase 5 Histone deacetylase activity (23,29,30) SETDB1 (ESET;KMT1E) SET domain, bifurcated 1 Histone-lysine N-methyltransferase activity (31-34) Transcription factors GTF3C2 general transcription factor IIIC, polypeptide 2, beta 110kDa Required for RNA polymerase III-mediated transcription HEYL (Hey3) hairy/enhancer-of-split related with YRPW motif-like DNA-binding transcription factor with basic helix-loop-helix domain (35) KLF10 (TIEG1) Kruppel-like factor 10 DNA-binding transcription factor with C2H2 zinc finger domain (36) NR2F1 (COUP-TFI) nuclear receptor subfamily 2, group F, member 1 DNA-binding transcription factor with C4 type zinc finger domain (ligand-regulated) (36) PEG3 paternally expressed 3 DNA-binding transcription factor with -

Integrative Analysis Reveals RNA G-Quadruplexes in Utrs Are Selectively Constrained and Enriched for Functional Associations
ARTICLE https://doi.org/10.1038/s41467-020-14404-y OPEN Integrative analysis reveals RNA G-quadruplexes in UTRs are selectively constrained and enriched for functional associations David S.M. Lee 1, Louis R. Ghanem 2* & Yoseph Barash 1,3* G-quadruplex (G4) sequences are abundant in untranslated regions (UTRs) of human messenger RNAs, but their functional importance remains unclear. By integrating multiple 1234567890():,; sources of genetic and genomic data, we show that putative G-quadruplex forming sequences (pG4) in 5’ and 3’ UTRs are selectively constrained, and enriched for cis-eQTLs and RNA-binding protein (RBP) interactions. Using over 15,000 whole-genome sequences, we find that negative selection acting on central guanines of UTR pG4s is comparable to that of missense variation in protein-coding sequences. At multiple GWAS-implicated SNPs within pG4 UTR sequences, we find robust allelic imbalance in gene expression across diverse tissue contexts in GTEx, suggesting that variants affecting G-quadruplex formation within UTRs may also contribute to phenotypic variation. Our results establish UTR G4s as important cis-regulatory elements and point to a link between disruption of UTR pG4 and disease. 1 Department of Genetics, Perelman School of Medicine, University of Pennsylvania, Philadelphia, PA 19104, USA. 2 Division of Gastroenterology, Hepatology and Nutrition, Department of Pediatrics, The Children’s Hospital of Philadelphia and The University of Pennsylvania Perelman School of Medicine, Philadelphia, PA 19104, USA. 3 Department -

Effect of Chromosomal Copy Number Variations on Congenital Birth Defects and Human Developmental Disorders
EFFECT OF CHROMOSOMAL COPY NUMBER VARIATIONS ON CONGENITAL BIRTH DEFECTS AND HUMAN DEVELOPMENTAL DISORDERS APPROVED BY SUPERVISORY COMMITTEE Andrew R. Zinn, M.D., Ph.D Christine K. Garcia, M.D., Ph.D Orson Moe, M.D., Ph.D Ralph DeBerardinis, M.D., Ph.D DEDICATION Many many people have given me love, support, advice, and caffeine over the course of my graduate research to which I am eternally grateful. To Andrew, my mentor for many years and scientific guide- if someday I become half the researcher you are, I will have turned out. There aren’t enough words- thank you, thank you, thank you. To my thesis committee- thank for your insightful comments, direction and criticism and most for your genuine desire to see me succeed. To my collaborators, Vidu Garg and Linda Baker- thank you for sharing your research with a lowly grad student. I would literally have nothing to research without your generosity. To the lab-thanks for listening to boring mitochondrial results each week. I will miss you terribly. To Miguel- No puedo poner a las palabras la profundidad de mi amor para usted. Usted es mi amigo, mi amor, mi corazón, mi amante, mi ayuda y mi ancla. Con usted por mi lado puedo lograr las cosas magníficas que no podría solamente. Te amo. To Justin- the talk of complex four late at night was worth it. Love you. To Kim, Kristen and Adriane- my absolute favorite people- thank you for believing even when I did not. Thank you for listening to me when I needed it most. -

Pluripotency Factors Regulate Definitive Endoderm Specification Through Eomesodermin
Downloaded from genesdev.cshlp.org on September 23, 2021 - Published by Cold Spring Harbor Laboratory Press Pluripotency factors regulate definitive endoderm specification through eomesodermin Adrian Kee Keong Teo,1,2 Sebastian J. Arnold,3 Matthew W.B. Trotter,1 Stephanie Brown,1 Lay Teng Ang,1 Zhenzhi Chng,1,2 Elizabeth J. Robertson,4 N. Ray Dunn,2,5 and Ludovic Vallier1,5,6 1Laboratory for Regenerative Medicine, University of Cambridge, Cambridge CB2 0SZ, United Kingdom; 2Institute of Medical Biology, A*STAR (Agency for Science, Technology, and Research), Singapore 138648; 3Renal Department, Centre for Clinical Research, University Medical Centre, 79106 Freiburg, Germany; 4Sir William Dunn School of Pathology, University of Oxford, Oxford OX1 3RE, United Kingdom Understanding the molecular mechanisms controlling early cell fate decisions in mammals is a major objective toward the development of robust methods for the differentiation of human pluripotent stem cells into clinically relevant cell types. Here, we used human embryonic stem cells and mouse epiblast stem cells to study specification of definitive endoderm in vitro. Using a combination of whole-genome expression and chromatin immunoprecipitation (ChIP) deep sequencing (ChIP-seq) analyses, we established an hierarchy of transcription factors regulating endoderm specification. Importantly, the pluripotency factors NANOG, OCT4, and SOX2 have an essential function in this network by actively directing differentiation. Indeed, these transcription factors control the expression of EOMESODERMIN (EOMES), which marks the onset of endoderm specification. In turn, EOMES interacts with SMAD2/3 to initiate the transcriptional network governing endoderm formation. Together, these results provide for the first time a comprehensive molecular model connecting the transition from pluripotency to endoderm specification during mammalian development. -

Histone-Binding of DPF2 Mediates Its Repressive Role in Myeloid Differentiation
Histone-binding of DPF2 mediates its repressive role in myeloid differentiation Ferdinand M. Hubera,1, Sarah M. Greenblattb,1, Andrew M. Davenporta,1, Concepcion Martinezb,YeXub,LyP.Vuc, Stephen D. Nimerb,2, and André Hoelza,2 aDivision of Chemistry and Chemical Engineering, California Institute of Technology, Pasadena, CA 91125; bSylvester Comprehensive Cancer Center, University of Miami Miller School of Medicine, Miami, FL 33136; and cMolecular Pharmacology Program, Memorial Sloan Kettering Cancer Center, New York, NY 10065 Edited by Douglas C. Rees, Howard Hughes Medical Institute, California Institute of Technology, Pasadena, CA, and approved April 26, 2017 (received for review January 6, 2017) Double plant homeodomain finger 2 (DPF2) is a highly evolution- RUNX1 form a methylation-dependent repressive complex in arily conserved member of the d4 protein family that is ubiqui- AML, although it remains unclear whether the two proteins bind tously expressed in human tissues and was recently shown to each other directly or act concertedly as part of a larger complex. inhibit the myeloid differentiation of hematopoietic stem/progen- Here, we present the crystal structure of the human DPF2 itor and acute myelogenous leukemia cells. Here, we present the tandem PHD finger domain at a 1.6-Å resolution. We demon- crystal structure of the tandem plant homeodomain finger domain strate that the DPF2 tandem PHD finger domain binds acetylated of human DPF2 at 1.6-Å resolution. We show that DPF2 interacts H3 and H4 histone tails, identify the primary determinants of with the acetylated tails of both histones 3 and 4 via bipartite histone recognition, and confirm these interactions in vivo. -

Watsonjn2018.Pdf (1.780Mb)
UNIVERSITY OF CENTRAL OKLAHOMA Edmond, Oklahoma Department of Biology Investigating Differential Gene Expression in vivo of Cardiac Birth Defects in an Avian Model of Maternal Phenylketonuria A THESIS SUBMITTED TO THE GRADUATE FACULTY In partial fulfillment of the requirements For the degree of MASTER OF SCIENCE IN BIOLOGY By Jamie N. Watson Edmond, OK June 5, 2018 J. Watson/Dr. Nikki Seagraves ii J. Watson/Dr. Nikki Seagraves Acknowledgements It is difficult to articulate the amount of gratitude I have for the support and encouragement I have received throughout my master’s thesis. Many people have added value and support to my life during this time. I am thankful for the education, experience, and friendships I have gained at the University of Central Oklahoma. First, I would like to thank Dr. Nikki Seagraves for her mentorship and friendship. I lucked out when I met her. I have enjoyed working on this project and I am very thankful for her support. I would like thank Thomas Crane for his support and patience throughout my master’s degree. I would like to thank Dr. Shannon Conley for her continued mentorship and support. I would like to thank Liz Bullen and Dr. Eric Howard for their training and help on this project. I would like to thank Kristy Meyer for her friendship and help throughout graduate school. I would like to thank my committee members Dr. Robert Brennan and Dr. Lilian Chooback for their advisement on this project. Also, I would like to thank the biology faculty and staff. I would like to thank the Seagraves lab members: Jailene Canales, Kayley Pate, Mckayla Muse, Grace Thetford, Kody Harvey, Jordan Guffey, and Kayle Patatanian for their hard work and support. -

A Computational Approach for Defining a Signature of Β-Cell Golgi Stress in Diabetes Mellitus
Page 1 of 781 Diabetes A Computational Approach for Defining a Signature of β-Cell Golgi Stress in Diabetes Mellitus Robert N. Bone1,6,7, Olufunmilola Oyebamiji2, Sayali Talware2, Sharmila Selvaraj2, Preethi Krishnan3,6, Farooq Syed1,6,7, Huanmei Wu2, Carmella Evans-Molina 1,3,4,5,6,7,8* Departments of 1Pediatrics, 3Medicine, 4Anatomy, Cell Biology & Physiology, 5Biochemistry & Molecular Biology, the 6Center for Diabetes & Metabolic Diseases, and the 7Herman B. Wells Center for Pediatric Research, Indiana University School of Medicine, Indianapolis, IN 46202; 2Department of BioHealth Informatics, Indiana University-Purdue University Indianapolis, Indianapolis, IN, 46202; 8Roudebush VA Medical Center, Indianapolis, IN 46202. *Corresponding Author(s): Carmella Evans-Molina, MD, PhD ([email protected]) Indiana University School of Medicine, 635 Barnhill Drive, MS 2031A, Indianapolis, IN 46202, Telephone: (317) 274-4145, Fax (317) 274-4107 Running Title: Golgi Stress Response in Diabetes Word Count: 4358 Number of Figures: 6 Keywords: Golgi apparatus stress, Islets, β cell, Type 1 diabetes, Type 2 diabetes 1 Diabetes Publish Ahead of Print, published online August 20, 2020 Diabetes Page 2 of 781 ABSTRACT The Golgi apparatus (GA) is an important site of insulin processing and granule maturation, but whether GA organelle dysfunction and GA stress are present in the diabetic β-cell has not been tested. We utilized an informatics-based approach to develop a transcriptional signature of β-cell GA stress using existing RNA sequencing and microarray datasets generated using human islets from donors with diabetes and islets where type 1(T1D) and type 2 diabetes (T2D) had been modeled ex vivo. To narrow our results to GA-specific genes, we applied a filter set of 1,030 genes accepted as GA associated. -

Neuronal Differentiation and Cell-Cycle Programs Mediate Response to BET-Bromodomain Inhibition in MYC-Driven Medulloblastoma
ARTICLE https://doi.org/10.1038/s41467-019-10307-9 OPEN Neuronal differentiation and cell-cycle programs mediate response to BET-bromodomain inhibition in MYC-driven medulloblastoma Pratiti Bandopadhayay et al.# BET-bromodomain inhibition (BETi) has shown pre-clinical promise for MYC-amplified medulloblastoma. However, the mechanisms for its action, and ultimately for resistance, have 1234567890():,; not been fully defined. Here, using a combination of expression profiling, genome-scale CRISPR/Cas9-mediated loss of function and ORF/cDNA driven rescue screens, and cell- based models of spontaneous resistance, we identify bHLH/homeobox transcription factors and cell-cycle regulators as key genes mediating BETi’s response and resistance. Cells that acquire drug tolerance exhibit a more neuronally differentiated cell-state and expression of lineage-specific bHLH/homeobox transcription factors. However, they do not terminally differentiate, maintain expression of CCND2, and continue to cycle through S-phase. Moreover, CDK4/CDK6 inhibition delays acquisition of resistance. Therefore, our data provide insights about the mechanisms underlying BETi effects and the appearance of resistance and support the therapeutic use of combined cell-cycle inhibitors with BETi in MYC-amplified medulloblastoma. Correspondence and requests for materials should be addressed to C.M.J. (email: [email protected]) or to R.B. (email: [email protected]). #A full list of authors and their affiliations appears at the end of the paper. NATURE COMMUNICATIONS | (2019) 10:2400 | https://doi.org/10.1038/s41467-019-10307-9 | www.nature.com/naturecommunications 1 ARTICLE NATURE COMMUNICATIONS | https://doi.org/10.1038/s41467-019-10307-9 YC-driven group 3 medulloblastoma is an aggressive Genes suppressed by BETi tend to be cell-essential. -
![Downloaded from [266]](https://docslib.b-cdn.net/cover/7352/downloaded-from-266-347352.webp)
Downloaded from [266]
Patterns of DNA methylation on the human X chromosome and use in analyzing X-chromosome inactivation by Allison Marie Cotton B.Sc., The University of Guelph, 2005 A THESIS SUBMITTED IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF DOCTOR OF PHILOSOPHY in The Faculty of Graduate Studies (Medical Genetics) THE UNIVERSITY OF BRITISH COLUMBIA (Vancouver) January 2012 © Allison Marie Cotton, 2012 Abstract The process of X-chromosome inactivation achieves dosage compensation between mammalian males and females. In females one X chromosome is transcriptionally silenced through a variety of epigenetic modifications including DNA methylation. Most X-linked genes are subject to X-chromosome inactivation and only expressed from the active X chromosome. On the inactive X chromosome, the CpG island promoters of genes subject to X-chromosome inactivation are methylated in their promoter regions, while genes which escape from X- chromosome inactivation have unmethylated CpG island promoters on both the active and inactive X chromosomes. The first objective of this thesis was to determine if the DNA methylation of CpG island promoters could be used to accurately predict X chromosome inactivation status. The second objective was to use DNA methylation to predict X-chromosome inactivation status in a variety of tissues. A comparison of blood, muscle, kidney and neural tissues revealed tissue-specific X-chromosome inactivation, in which 12% of genes escaped from X-chromosome inactivation in some, but not all, tissues. X-linked DNA methylation analysis of placental tissues predicted four times higher escape from X-chromosome inactivation than in any other tissue. Despite the hypomethylation of repetitive elements on both the X chromosome and the autosomes, no changes were detected in the frequency or intensity of placental Cot-1 holes. -

Modulating Hallmarks of Cholangiocarcinoma
University of Nebraska Medical Center DigitalCommons@UNMC Theses & Dissertations Graduate Studies Fall 12-14-2018 Modulating Hallmarks of Cholangiocarcinoma Cody Wehrkamp University of Nebraska Medical Center Follow this and additional works at: https://digitalcommons.unmc.edu/etd Part of the Molecular Biology Commons Recommended Citation Wehrkamp, Cody, "Modulating Hallmarks of Cholangiocarcinoma" (2018). Theses & Dissertations. 337. https://digitalcommons.unmc.edu/etd/337 This Dissertation is brought to you for free and open access by the Graduate Studies at DigitalCommons@UNMC. It has been accepted for inclusion in Theses & Dissertations by an authorized administrator of DigitalCommons@UNMC. For more information, please contact [email protected]. MODULATING HALLMARKS OF CHOLANGIOCARCINOMA by Cody J. Wehrkamp A DISSERTATION Presented to the Faculty of the University of Nebraska Graduate College in Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy Biochemistry and Molecular Biology Graduate Program Under the Supervision of Professor Justin L. Mott University of Nebraska Medical Center Omaha, Nebraska November 2018 Supervisory Committee: Kaustubh Datta, Ph.D. Melissa Teoh‐Fitzgerald, Ph.D. Richard G. MacDonald, Ph.D. Acknowledgements This endeavor has led to scientific as well as personal growth for me. I am indebted to many for their knowledge, influence, and support along the way. To my mentor, Dr. Justin L. Mott, you have been an incomparable teacher and invaluable guide. You upheld for me the concept that science is intrepid, even when the experience is trying. Through my training, and now here at the end, I can say that it has been an honor to be your protégé. When you have shaped your future graduates to be and do great, I will be privileged to say that I was your first one.