Classification K-Nearest Neighbor Classifier Naïve Bayes Logistic
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

Small-Sample Properties of Tests for Heteroscedasticity in the Conditional Logit Model
HEDG Working Paper 06/04 Small-sample properties of tests for heteroscedasticity in the conditional logit model Arne Risa Hole May 2006 ISSN 1751-1976 york.ac.uk/res/herc/hedgwp Small-sample properties of tests for heteroscedasticity in the conditional logit model Arne Risa Hole National Primary Care Research and Development Centre Centre for Health Economics University of York May 16, 2006 Abstract This paper compares the small-sample properties of several asymp- totically equivalent tests for heteroscedasticity in the conditional logit model. While no test outperforms the others in all of the experiments conducted, the likelihood ratio test and a particular variety of the Wald test are found to have good properties in moderate samples as well as being relatively powerful. Keywords: conditional logit, heteroscedasticity JEL classi…cation: C25 National Primary Care Research and Development Centre, Centre for Health Eco- nomics, Alcuin ’A’Block, University of York, York YO10 5DD, UK. Tel.: +44 1904 321404; fax: +44 1904 321402. E-mail address: [email protected]. NPCRDC receives funding from the Department of Health. The views expressed are not necessarily those of the funders. 1 1 Introduction In most applications of the conditional logit model the error term is assumed to be homoscedastic. Recently, however, there has been a growing interest in testing the homoscedasticity assumption in applied work (Hensher et al., 1999; DeShazo and Fermo, 2002). This is partly due to the well-known result that heteroscedasticity causes the coe¢ cient estimates in discrete choice models to be inconsistent (Yatchew and Griliches, 1985), but also re‡ects a behavioural interest in factors in‡uencing the variance of the latent variables in the model (Louviere, 2001; Louviere et al., 2002). -

Multinomial Logistic Regression
26-Osborne (Best)-45409.qxd 10/9/2007 5:52 PM Page 390 26 MULTINOMIAL LOGISTIC REGRESSION CAROLYN J. ANDERSON LESLIE RUTKOWSKI hapter 24 presented logistic regression Many of the concepts used in binary logistic models for dichotomous response vari- regression, such as the interpretation of parame- C ables; however, many discrete response ters in terms of odds ratios and modeling prob- variables have three or more categories (e.g., abilities, carry over to multicategory logistic political view, candidate voted for in an elec- regression models; however, two major modifica- tion, preferred mode of transportation, or tions are needed to deal with multiple categories response options on survey items). Multicate- of the response variable. One difference is that gory response variables are found in a wide with three or more levels of the response variable, range of experiments and studies in a variety of there are multiple ways to dichotomize the different fields. A detailed example presented in response variable. If J equals the number of cate- this chapter uses data from 600 students from gories of the response variable, then J(J – 1)/2 dif- the High School and Beyond study (Tatsuoka & ferent ways exist to dichotomize the categories. Lohnes, 1988) to look at the differences among In the High School and Beyond study, the three high school students who attended academic, program types can be dichotomized into pairs general, or vocational programs. The students’ of programs (i.e., academic and general, voca- socioeconomic status (ordinal), achievement tional and general, and academic and vocational). test scores (numerical), and type of school How the response variable is dichotomized (nominal) are all examined as possible explana- depends, in part, on the nature of the variable. -

Logit and Ordered Logit Regression (Ver
Getting Started in Logit and Ordered Logit Regression (ver. 3.1 beta) Oscar Torres-Reyna Data Consultant [email protected] http://dss.princeton.edu/training/ PU/DSS/OTR Logit model • Use logit models whenever your dependent variable is binary (also called dummy) which takes values 0 or 1. • Logit regression is a nonlinear regression model that forces the output (predicted values) to be either 0 or 1. • Logit models estimate the probability of your dependent variable to be 1 (Y=1). This is the probability that some event happens. PU/DSS/OTR Logit odelm From Stock & Watson, key concept 9.3. The logit model is: Pr(YXXXFXX 1 | 1= , 2 ,...=k β ) +0 β ( 1 +2 β 1 +βKKX 2 + ... ) 1 Pr(YXXX 1= | 1 , 2k = ,... ) 1−+(eβ0 + βXX 1 1 + β 2 2 + ...βKKX + ) 1 Pr(YXXX 1= | 1 , 2= ,... ) k ⎛ 1 ⎞ 1+ ⎜ ⎟ (⎝ eβ+0 βXX 1 1 + β 2 2 + ...βKK +X ⎠ ) Logit nd probita models are basically the same, the difference is in the distribution: • Logit – Cumulative standard logistic distribution (F) • Probit – Cumulative standard normal distribution (Φ) Both models provide similar results. PU/DSS/OTR It tests whether the combined effect, of all the variables in the model, is different from zero. If, for example, < 0.05 then the model have some relevant explanatory power, which does not mean it is well specified or at all correct. Logit: predicted probabilities After running the model: logit y_bin x1 x2 x3 x4 x5 x6 x7 Type predict y_bin_hat /*These are the predicted probabilities of Y=1 */ Here are the estimations for the first five cases, type: 1 x2 x3 x4 x5 x6 x7 y_bin_hatbrowse y_bin x Predicted probabilities To estimate the probability of Y=1 for the first row, replace the values of X into the logit regression equation. -

Lecture 9: Logit/Probit Prof
Lecture 9: Logit/Probit Prof. Sharyn O’Halloran Sustainable Development U9611 Econometrics II Review of Linear Estimation So far, we know how to handle linear estimation models of the type: Y = β0 + β1*X1 + β2*X2 + … + ε ≡ Xβ+ ε Sometimes we had to transform or add variables to get the equation to be linear: Taking logs of Y and/or the X’s Adding squared terms Adding interactions Then we can run our estimation, do model checking, visualize results, etc. Nonlinear Estimation In all these models Y, the dependent variable, was continuous. Independent variables could be dichotomous (dummy variables), but not the dependent var. This week we’ll start our exploration of non- linear estimation with dichotomous Y vars. These arise in many social science problems Legislator Votes: Aye/Nay Regime Type: Autocratic/Democratic Involved in an Armed Conflict: Yes/No Link Functions Before plunging in, let’s introduce the concept of a link function This is a function linking the actual Y to the estimated Y in an econometric model We have one example of this already: logs Start with Y = Xβ+ ε Then change to log(Y) ≡ Y′ = Xβ+ ε Run this like a regular OLS equation Then you have to “back out” the results Link Functions Before plunging in, let’s introduce the concept of a link function This is a function linking the actual Y to the estimated Y in an econometric model We have one example of this already: logs Start with Y = Xβ+ ε Different β’s here Then change to log(Y) ≡ Y′ = Xβ + ε Run this like a regular OLS equation Then you have to “back out” the results Link Functions If the coefficient on some particular X is β, then a 1 unit ∆X Æ β⋅∆(Y′) = β⋅∆[log(Y))] = eβ ⋅∆(Y) Since for small values of β, eβ ≈ 1+β , this is almost the same as saying a β% increase in Y (This is why you should use natural log transformations rather than base-10 logs) In general, a link function is some F(⋅) s.t. -

Generalized Linear Models
CHAPTER 6 Generalized linear models 6.1 Introduction Generalized linear modeling is a framework for statistical analysis that includes linear and logistic regression as special cases. Linear regression directly predicts continuous data y from a linear predictor Xβ = β0 + X1β1 + + Xkβk.Logistic regression predicts Pr(y =1)forbinarydatafromalinearpredictorwithaninverse-··· logit transformation. A generalized linear model involves: 1. A data vector y =(y1,...,yn) 2. Predictors X and coefficients β,formingalinearpredictorXβ 1 3. A link function g,yieldingavectoroftransformeddataˆy = g− (Xβ)thatare used to model the data 4. A data distribution, p(y yˆ) | 5. Possibly other parameters, such as variances, overdispersions, and cutpoints, involved in the predictors, link function, and data distribution. The options in a generalized linear model are the transformation g and the data distribution p. In linear regression,thetransformationistheidentity(thatis,g(u) u)and • the data distribution is normal, with standard deviation σ estimated from≡ data. 1 1 In logistic regression,thetransformationistheinverse-logit,g− (u)=logit− (u) • (see Figure 5.2a on page 80) and the data distribution is defined by the proba- bility for binary data: Pr(y =1)=y ˆ. This chapter discusses several other classes of generalized linear model, which we list here for convenience: The Poisson model (Section 6.2) is used for count data; that is, where each • data point yi can equal 0, 1, 2, ....Theusualtransformationg used here is the logarithmic, so that g(u)=exp(u)transformsacontinuouslinearpredictorXiβ to a positivey ˆi.ThedatadistributionisPoisson. It is usually a good idea to add a parameter to this model to capture overdis- persion,thatis,variationinthedatabeyondwhatwouldbepredictedfromthe Poisson distribution alone. -

A Generalized Gaussian Process Model for Computer Experiments with Binary Time Series
A Generalized Gaussian Process Model for Computer Experiments with Binary Time Series Chih-Li Sunga 1, Ying Hungb 1, William Rittasec, Cheng Zhuc, C. F. J. Wua 2 aSchool of Industrial and Systems Engineering, Georgia Institute of Technology bDepartment of Statistics, Rutgers, the State University of New Jersey cDepartment of Biomedical Engineering, Georgia Institute of Technology Abstract Non-Gaussian observations such as binary responses are common in some computer experiments. Motivated by the analysis of a class of cell adhesion experiments, we introduce a generalized Gaussian process model for binary responses, which shares some common features with standard GP models. In addition, the proposed model incorporates a flexible mean function that can capture different types of time series structures. Asymptotic properties of the estimators are derived, and an optimal predictor as well as its predictive distribution are constructed. Their performance is examined via two simulation studies. The methodology is applied to study computer simulations for cell adhesion experiments. The fitted model reveals important biological information in repeated cell bindings, which is not directly observable in lab experiments. Keywords: Computer experiment, Gaussian process model, Single molecule experiment, Uncertainty quantification arXiv:1705.02511v4 [stat.ME] 24 Sep 2018 1Joint first authors. 2Corresponding author. 1 1 Introduction Cell adhesion plays an important role in many physiological and pathological processes. This research is motivated by the analysis of a class of cell adhesion experiments called micropipette adhesion frequency assays, which is a method for measuring the kinetic rates between molecules in their native membrane environment. In a micropipette adhesion frequency assay, a red blood coated in a specific ligand is brought into contact with cell containing the native receptor for a predetermined duration, then retracted. -

Week 12: Linear Probability Models, Logistic and Probit
Week 12: Linear Probability Models, Logistic and Probit Marcelo Coca Perraillon University of Colorado Anschutz Medical Campus Health Services Research Methods I HSMP 7607 2019 These slides are part of a forthcoming book to be published by Cambridge University Press. For more information, go to perraillon.com/PLH. c This material is copyrighted. Please see the entire copyright notice on the book's website. Updated notes are here: https://clas.ucdenver.edu/marcelo-perraillon/ teaching/health-services-research-methods-i-hsmp-7607 1 Outline Modeling 1/0 outcomes The \wrong" but super useful model: Linear Probability Model Deriving logistic regression Probit regression as an alternative 2 Binary outcomes Binary outcomes are everywhere: whether a person died or not, broke a hip, has hypertension or diabetes, etc We typically want to understand what is the probability of the binary outcome given explanatory variables It's exactly the same type of models we have seen during the semester, the difference is that we have been modeling the conditional expectation given covariates: E[Y jX ] = β0 + β1X1 + ··· + βpXp Now, we want to model the probability given covariates: P(Y = 1jX ) = f (β0 + β1X1 + ··· + βpXp) Note the function f() in there 3 Linear Probability Models We could actually use our vanilla linear model to do so If Y is an indicator or dummy variable, then E[Y jX ] is the proportion of 1s given X , which we interpret as the probability of Y given X The parameters are changes/effects/differences in the probability of Y by a unit change in X or for a small change in X If an indicator variable, then change from 0 to 1 For example, if we model diedi = β0 + β1agei + i , we could interpret β1 as the change in the probability of death for an additional year of age 4 Linear Probability Models The problem is that we know that this model is not entirely correct. -
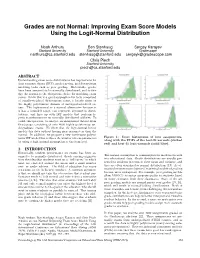
Improving Exam Score Models Using the Logit-Normal Distribution
Grades are not Normal: Improving Exam Score Models Using the Logit-Normal Distribution Noah Arthurs Ben Stenhaug Sergey Karayev Stanford University Stanford University Gradescope [email protected] [email protected] [email protected] Chris Piech Stanford University [email protected] ABSTRACT Understanding exam score distributions has implications for item response theory (IRT), grade curving, and downstream modeling tasks such as peer grading. Historically, grades have been assumed to be normally distributed, and to this day the normal is the ubiquitous choice for modeling exam scores. While this is a good assumption for tests comprised 0.2 0.4 0.6 0.8 0.2 0.4 0.6 0.8 of equally-weighted dichotomous items, it breaks down on Norm ali zed Exa m Score Normalized Exa m Score the highly polytomous domain of undergraduate-level ex- ams. The logit-normal is a natural alternative because it is has a bounded range, can represent asymmetric distri- butions, and lines up with IRT models that perform lo- gistic transformations on normally distributed abilities. To tackle this question, we analyze an anonymized dataset from Gradescope consisting of over 4000 highly polytomous un- dergraduate exams. We show that the logit-normal better 0.2 0.4 0.6 0.8 0.4 0.6 0.8 Normalized Exa m Score Norm ali zed Exa m Score models this data without having more parameters than the normal. In addition, we propose a new continuous polyto- mous IRT model that reduces the number of item-parameters Figure 1: Score histograms of four assignments, by using a logit-normal assumption at the item level. -

Modeling Bounded Outcome Scores Using the Binomial-Logit-Normal Distribution
Chilean Journal of Statistics Vol. 5, No. 2, September 2014, 3{14 Generalized Linear Models Research Paper Modeling Bounded Outcome Scores Using The Binomial-Logit-Normal Distribution Ye Liang1;∗, Dongchu Sun2, Chong He2 and Mario Schootman3 1Department of Statistics, Oklahoma State University, Stillwater, USA, 2Department of Statistics, University of Missouri, Columbia, USA, 3Washington University School of Medicine, St. Louis, USA (Received: 23 September 2013 · Accepted in final form: 30 September 2014) Abstract Bounded outcome scores are often encountered in health-related survey studies. Such scores are usually bounded and discrete and are often treated as categorical or ordinal data, which is not satisfactory in some scenarios. The binomial-logit-normal distribution, as a parametric model, is a useful alternative for the bounded outcome scores. The proposed model converges to the continuous logit-normal model and hence bridges the gap between discrete modeling and continuous modeling. This result is useful when the score is dense and smooth within its bounded support. A quality of life data is shown as an application. Keywords: health outcome · binomial-logit-normal · ordinal data · logistic regression · quality of life. Mathematics Subject Classification: Primary 60F05 · Secondary 62J12. 1. Introduction Bounded outcome scores are encountered in many survey studies, especially in survey studies involving health assessment. Examples are the Barthel index, drug compliance studies, pain relief studies and quality of life (QOL) studies (Lesaffre et al., 2007). In this paper, we present a QOL study as our motivation example. This is a survey study on breast cancer survivors, investigating their health-related QOL and comparing their QOL with that of community-dwelling women without any type of reportable cancer. -

Logit and Probit Models
York SPIDA John Fox Notes Logit and Probit Models Copyright © 2010 by John Fox Logit and Probit Models 1 1. Topics I Models for dichotmous data I Models for polytomous data (as time permits) I Implementation of logit and probit models in R c 2010 by John Fox York SPIDA ° Logit and Probit Models 2 2. Models for Dichotomous Data I To understand why logit and probit models for qualitative data are required, let us begin by examining a representative problem, attempting to apply linear regression to it: In September of 1988, 15 years after the coup of 1973, the people • of Chile voted in a plebiscite to decide the future of the military government. A ‘yes’ vote would represent eight more years of military rule; a ‘no’ vote would return the country to civilian government. The no side won the plebiscite, by a clear if not overwhelming margin. Six months before the plebiscite, FLACSO/Chile conducted a national • survey of 2,700 randomly selected Chilean voters. Of these individuals, 868 said that they were planning to vote yes, · and 889 said that they were planning to vote no. Of the remainder, 558 said that they were undecided, 187 said that · they planned to abstain, and 168 did not answer the question. c 2010 by John Fox York SPIDA ° Logit and Probit Models 3 I will look only at those who expressed a preference. · Figure 1 plots voting intention against a measure of support for the • status quo. Voting intention appears as a dummy variable, coded 1 for yes, 0 for · no. -

Logistic Regression
Newsom Psy 526/626 Multilevel Regression, Spring 2019 1 Logistic Regression Logistic regression involves a prediction equation in which one or more explanatory (predictor) variables is used to provide information about expected values of a binary response (dependent) variable. Ordinary least squares regression assumes that Y is distributed approximately normally in the population, and, because a binary response variable will not be normal, we need to consider a different type of model. Predicting the Probability that Y = 1 For a binary response variable, we can frame the prediction equation in terms of the probability of a discrete event occurring. Usual coding of the response variable is 0 and 1, with the event of interest (e.g., “yes” response, occurrence of an aggressive behavior, or heart attack), so that, if X and Y have a positive linear relationship, the probability that a person will have a score of Y = 1 will increase as values of X increase. For example, we might try to predict whether or not a couple is divorced based on the age of their youngest child. Does the probability of divorce (Y = 1) increase as the youngest child’s age (X) increases? If we take a hypothetical example, in which there were 50 couples studied and the children have a range of ages from 0 to 20 years, we could represent this tendency to increase the probability that Y = 1 with a graph, grouping child ages into four-year intervals for the purposes of illustration. Assuming codes of 0 and 1 for Y, the average value in each four-year period is the same as the estimated probability of divorce for that age group. -

Generalized Linear Models Link Function the Logistic Equation Is
Newsom Psy 525/625 Categorical Data Analysis, Spring 2021 1 Generalized Linear Models Link Function The logistic equation is stated in terms of the probability that Y = 1, which is π, and the probability that Y = 0, which is 1 - π. π ln =αβ + X 1−π The left-hand side of the equation represents the logit transformation, which takes the natural log of the ratio of the probability that Y is equal to 1 compared to the probability that it is not equal to one. As we know, the probability, π, is just the mean of the Y values, assuming 0,1 coding, which is often expressed as µ. The logit transformation could then be written in terms of the mean rather than the probability, µ ln =αβ + X 1− µ The transformation of the mean represents a link to the central tendency of the distribution, sometimes called the location, one of the important defining aspects of any given probability distribution. The log transformation represents a kind of link function (often canonical link function)1 that is sometimes given more generally as g(.), with the letter g used as an arbitrary name for a mathematical function and the use of the “.” within the parentheses to suggest that any variable, value, or function (the argument) could be placed within. For logistic regression, this is known as the logit link function. The right hand side of the equation, α + βX, is the familiar equation for the regression line and represents a linear combination of the parameters for the regression. The concept of this logistic link function can generalized to any other distribution, with the simplest, most familiar case being the ordinary least squares or linear regression model.