Asteroid Rotations 113
Total Page:16
File Type:pdf, Size:1020Kb

Load more
Recommended publications
-

New Voyage to Rendezvous with a Small Asteroid Rotating with a Short Period
Hayabusa2 Extended Mission: New Voyage to Rendezvous with a Small Asteroid Rotating with a Short Period M. Hirabayashi1, Y. Mimasu2, N. Sakatani3, S. Watanabe4, Y. Tsuda2, T. Saiki2, S. Kikuchi2, T. Kouyama5, M. Yoshikawa2, S. Tanaka2, S. Nakazawa2, Y. Takei2, F. Terui2, H. Takeuchi2, A. Fujii2, T. Iwata2, K. Tsumura6, S. Matsuura7, Y. Shimaki2, S. Urakawa8, Y. Ishibashi9, S. Hasegawa2, M. Ishiguro10, D. Kuroda11, S. Okumura8, S. Sugita12, T. Okada2, S. Kameda3, S. Kamata13, A. Higuchi14, H. Senshu15, H. Noda16, K. Matsumoto16, R. Suetsugu17, T. Hirai15, K. Kitazato18, D. Farnocchia19, S.P. Naidu19, D.J. Tholen20, C.W. Hergenrother21, R.J. Whiteley22, N. A. Moskovitz23, P.A. Abell24, and the Hayabusa2 extended mission study group. 1Auburn University, Auburn, AL, USA ([email protected]) 2Japan Aerospace Exploration Agency, Kanagawa, Japan 3Rikkyo University, Tokyo, Japan 4Nagoya University, Aichi, Japan 5National Institute of Advanced Industrial Science and Technology, Tokyo, Japan 6Tokyo City University, Tokyo, Japan 7Kwansei Gakuin University, Hyogo, Japan 8Japan Spaceguard Association, Okayama, Japan 9Hosei University, Tokyo, Japan 10Seoul National University, Seoul, South Korea 11Kyoto University, Kyoto, Japan 12University of Tokyo, Tokyo, Japan 13Hokkaido University, Hokkaido, Japan 14University of Occupational and Environmental Health, Fukuoka, Japan 15Chiba Institute of Technology, Chiba, Japan 16National Astronomical Observatory of Japan, Iwate, Japan 17National Institute of Technology, Oshima College, Yamaguchi, Japan 18University of Aizu, Fukushima, Japan 19Jet Propulsion Laboratory, California Institute of Technology, Pasadena, CA, USA 20University of Hawai’i, Manoa, HI, USA 21University of Arizona, Tucson, AZ, USA 22Asgard Research, Denver, CO, USA 23Lowell Observatory, Flagstaff, AZ, USA 24NASA Johnson Space Center, Houston, TX, USA 1 Highlights 1. -
Potential Resources on and from the Asteroids/Comets; Threats
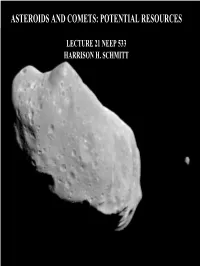
ASTEROIDS AND COMETS: POTENTIAL RESOURCES LECTURE 21 NEEP 533 HARRISON H. SCHMITT EROS C-TYPE NASA/NEAR SHOEMAKER/APL 11X11X34 KM ASTEROIDS IN GENERAL 1.3 GM/CM3 MAIN BELT ASTEROIDS BETWEEN JUPITER AND MARS NEAR EARTH ASTEROIDS SOME MAY BE SPENT COMETS EARTH CROSSING ASTEROIDS SOME MAY BE SPENT COMETS “CENTAUR” ASTEROIDS BETWEEN JUPITER AND URANUS CHIRON, 1979 VA, AND 133P/ELST-PIZARRO ALSO HAVE COMET- LIKE BEHAVIOR “TROJAN” ASTEROIDS JUPITER’S ORBIT AND CONTROLLED BY IT GENERAL CHARACTERISTICS RUBBLE PILES (?) NO ASTEROID >150M ROTATES FASTER THAN ONE REVOLUTION PER 2 HOURS CALCULATED LIMIT FOR RUBBLE TO STAY TOGETHER 1998 KY26 IS 30M IN DIAMETER, ROTATES IN 10.7 MIN. AND MAY BE SOLID MAY BE A TRANSITION IN ORBITAL CHARACTERISTICS AND / OR COMPOSITION BETWEEN SOME ASTEROIDS AND COMETS • S-TYPE OTHER ASTEROIDS – INNER ASTEROID BELT – EVIDENCE OF HEATING AND DIFFERENTIATION – 29 TELESCOPIC SPECTRA (Binzel, et al., 1996) • INTERMEDIATE BETWEEN S-TYPE AND ORDINARY CHONDRITES – 1. DISTINCT ROCK TYPES VS DIVERSE LARGER BODIES – 2. ABUNDANCE OF OPAQUE MATERIALS – 3. FRESH SURFACES (MOST LIKELY) • BASALTIC ACHONDRITES (6%) – 4 VESTA AT 2.36 AU [MAIN BELT PARENT (?)] – TOUTATIS - NEA (RADAR STUDY) • 4.5X2.4X1.9KM, 2.1 GM/CM3, TWO ROTATIONS, I.E., TUMBLING (5.4 AND 7.3 DAYS) – 1459 MAGNYA AT 3.15 AU [FRAGMENT OF LARGER BODY (?)] EROS • (Lazzaro, et al, 2000, Science, 288) C-TYPE (REVISED BY GRS DATA) 11X11X33 KM 2.7 GM/CM3 5.27 HR ROTATION NASA/NEAR SHOEMAKER/APL OTHER ASTEROIDS • D-TYPE CARBONACEOUS CHONDRITE (BEYOND MAIN BELT ASTEROIDS) – TAGISH -

Photometry of Asteroids: Lightcurves of 24 Asteroids Obtained in 1993–2005
ARTICLE IN PRESS Planetary and Space Science 55 (2007) 986–997 www.elsevier.com/locate/pss Photometry of asteroids: Lightcurves of 24 asteroids obtained in 1993–2005 V.G. Chiornya,b,Ã, V.G. Shevchenkoa, Yu.N. Kruglya,b, F.P. Velichkoa, N.M. Gaftonyukc aInstitute of Astronomy of Kharkiv National University, Sumska str. 35, 61022 Kharkiv, Ukraine bMain Astronomical Observatory, NASU, Zabolotny str. 27, Kyiv 03680, Ukraine cCrimean Astrophysical Observatory, Crimea, 98680 Simeiz, Ukraine Received 19 May 2006; received in revised form 23 December 2006; accepted 10 January 2007 Available online 21 January 2007 Abstract The results of 1993–2005 photometric observations for 24 main-belt asteroids: 24 Themis, 51 Nemausa, 89 Julia, 205 Martha, 225 Henrietta, 387 Aquitania, 423 Diotima, 505 Cava, 522 Helga, 543 Charlotte, 663 Gerlinde, 670 Ottegebe, 693 Zerbinetta, 694 Ekard, 713 Luscinia, 800 Kressmania, 1251 Hedera, 1369 Ostanina, 1427 Ruvuma, 1796 Riga, 2771 Polzunov, 4908 Ward, 6587 Brassens and 16541 1991 PW18 are presented. The rotation periods of nine of these asteroids have been determined for the first time and others have been improved. r 2007 Elsevier Ltd. All rights reserved. Keywords: Asteroids; Photometry; Lightcurve; Rotational period; Amplitude 1. Introduction telescope of the Crimean Astrophysics Observatory in Simeiz. Ground-based observations are the main source of knowledge about the physical properties of the asteroid 2. Observations and their reduction population. The photometric lightcurves are used to determine rotation periods, pole coordinates, sizes and Photometric observations of the asteroids were carried shapes of asteroids, as well as to study the magnitude-phase out in 1993–1994 using one-channel photoelectric photo- relation of different type asteroids. -

The Minor Planet Bulletin
THE MINOR PLANET BULLETIN OF THE MINOR PLANETS SECTION OF THE BULLETIN ASSOCIATION OF LUNAR AND PLANETARY OBSERVERS VOLUME 36, NUMBER 3, A.D. 2009 JULY-SEPTEMBER 77. PHOTOMETRIC MEASUREMENTS OF 343 OSTARA Our data can be obtained from http://www.uwec.edu/physics/ AND OTHER ASTEROIDS AT HOBBS OBSERVATORY asteroid/. Lyle Ford, George Stecher, Kayla Lorenzen, and Cole Cook Acknowledgements Department of Physics and Astronomy University of Wisconsin-Eau Claire We thank the Theodore Dunham Fund for Astrophysics, the Eau Claire, WI 54702-4004 National Science Foundation (award number 0519006), the [email protected] University of Wisconsin-Eau Claire Office of Research and Sponsored Programs, and the University of Wisconsin-Eau Claire (Received: 2009 Feb 11) Blugold Fellow and McNair programs for financial support. References We observed 343 Ostara on 2008 October 4 and obtained R and V standard magnitudes. The period was Binzel, R.P. (1987). “A Photoelectric Survey of 130 Asteroids”, found to be significantly greater than the previously Icarus 72, 135-208. reported value of 6.42 hours. Measurements of 2660 Wasserman and (17010) 1999 CQ72 made on 2008 Stecher, G.J., Ford, L.A., and Elbert, J.D. (1999). “Equipping a March 25 are also reported. 0.6 Meter Alt-Azimuth Telescope for Photometry”, IAPPP Comm, 76, 68-74. We made R band and V band photometric measurements of 343 Warner, B.D. (2006). A Practical Guide to Lightcurve Photometry Ostara on 2008 October 4 using the 0.6 m “Air Force” Telescope and Analysis. Springer, New York, NY. located at Hobbs Observatory (MPC code 750) near Fall Creek, Wisconsin. -

Dynamical Evolution of the Cybele Asteroids
MNRAS 451, 244–256 (2015) doi:10.1093/mnras/stv997 Dynamical evolution of the Cybele asteroids Downloaded from https://academic.oup.com/mnras/article-abstract/451/1/244/1381346 by Universidade Estadual Paulista J�lio de Mesquita Filho user on 22 April 2019 V. Carruba,1‹ D. Nesvorny,´ 2 S. Aljbaae1 andM.E.Huaman1 1UNESP, Univ. Estadual Paulista, Grupo de dinamicaˆ Orbital e Planetologia, 12516-410 Guaratingueta,´ SP, Brazil 2Department of Space Studies, Southwest Research Institute, Boulder, CO 80302, USA Accepted 2015 May 1. Received 2015 May 1; in original form 2015 April 1 ABSTRACT The Cybele region, located between the 2J:-1A and 5J:-3A mean-motion resonances, is ad- jacent and exterior to the asteroid main belt. An increasing density of three-body resonances makes the region between the Cybele and Hilda populations dynamically unstable, so that the Cybele zone could be considered the last outpost of an extended main belt. The presence of binary asteroids with large primaries and small secondaries suggested that asteroid families should be found in this region, but only relatively recently the first dynamical groups were identified in this area. Among these, the Sylvia group has been proposed to be one of the oldest families in the extended main belt. In this work we identify families in the Cybele region in the context of the local dynamics and non-gravitational forces such as the Yarkovsky and stochastic Yarkovsky–O’Keefe–Radzievskii–Paddack (YORP) effects. We confirm the detec- tion of the new Helga group at 3.65 au, which could extend the outer boundary of the Cybele region up to the 5J:-3A mean-motion resonance. -

Observations from Orbiting Platforms 219
Dotto et al.: Observations from Orbiting Platforms 219 Observations from Orbiting Platforms E. Dotto Istituto Nazionale di Astrofisica Osservatorio Astronomico di Torino M. A. Barucci Observatoire de Paris T. G. Müller Max-Planck-Institut für Extraterrestrische Physik and ISO Data Centre A. D. Storrs Towson University P. Tanga Istituto Nazionale di Astrofisica Osservatorio Astronomico di Torino and Observatoire de Nice Orbiting platforms provide the opportunity to observe asteroids without limitation by Earth’s atmosphere. Several Earth-orbiting observatories have been successfully operated in the last decade, obtaining unique results on asteroid physical properties. These include the high-resolu- tion mapping of the surface of 4 Vesta and the first spectra of asteroids in the far-infrared wave- length range. In the near future other space platforms and orbiting observatories are planned. Some of them are particularly promising for asteroid science and should considerably improve our knowledge of the dynamical and physical properties of asteroids. 1. INTRODUCTION 1800 asteroids. The results have been widely presented and discussed in the IRAS Minor Planet Survey (Tedesco et al., In the last few decades the use of space platforms has 1992) and the Supplemental IRAS Minor Planet Survey opened up new frontiers in the study of physical properties (Tedesco et al., 2002). This survey has been very important of asteroids by overcoming the limits imposed by Earth’s in the new assessment of the asteroid population: The aster- atmosphere and taking advantage of the use of new tech- oid taxonomy by Barucci et al. (1987), its recent extension nologies. (Fulchignoni et al., 2000), and an extended study of the size Earth-orbiting satellites have the advantage of observing distribution of main-belt asteroids (Cellino et al., 1991) are out of the terrestrial atmosphere; this allows them to be in just a few examples of the impact factor of this survey. -

Asteroid Retrieval Feasibility Study
Asteroid Retrieval Feasibility Study 2 April 2012 Prepared for the: Keck Institute for Space Studies California Institute of Technology Jet Propulsion Laboratory Pasadena, California 1 2 Authors and Study Participants NAME Organization E-Mail Signature John Brophy Co-Leader / NASA JPL / Caltech [email protected] Fred Culick Co-Leader / Caltech [email protected] Co -Leader / The Planetary Louis Friedman [email protected] Society Carlton Allen NASA JSC [email protected] David Baughman Naval Postgraduate School [email protected] NASA ARC/Carnegie Mellon Julie Bellerose [email protected] University Bruce Betts The Planetary Society [email protected] Mike Brown Caltech [email protected] Michael Busch UCLA [email protected] John Casani NASA JPL [email protected] Marcello Coradini ESA [email protected] John Dankanich NASA GRC [email protected] Paul Dimotakis Caltech [email protected] Harvard -Smithsonian Center for Martin Elvis [email protected] Astrophysics Ian Garrick-Bethel UCSC [email protected] Bob Gershman NASA JPL [email protected] Florida Institute for Human and Tom Jones [email protected] Machine Cognition Damon Landau NASA JPL [email protected] Chris Lewicki Arkyd Astronautics [email protected] John Lewis University of Arizona [email protected] Pedro Llanos USC [email protected] Mark Lupisella NASA GSFC [email protected] Dan Mazanek NASA LaRC [email protected] Prakhar Mehrotra Caltech [email protected] -

CURRICULUM VITAE, ALAN W. HARRIS Personal: Born
CURRICULUM VITAE, ALAN W. HARRIS Personal: Born: August 3, 1944, Portland, OR Married: August 22, 1970, Rose Marie Children: W. Donald (b. 1974), David (b. 1976), Catherine (b 1981) Education: B.S. (1966) Caltech, Geophysics M.S. (1967) UCLA, Earth and Space Science PhD. (1975) UCLA, Earth and Space Science Dissertation: Dynamical Studies of Satellite Origin. Advisor: W.M. Kaula Employment: 1966-1967 Graduate Research Assistant, UCLA 1968-1970 Member of Tech. Staff, Space Division Rockwell International 1970-1971 Physics instructor, Santa Monica College 1970-1973 Physics Teacher, Immaculate Heart High School, Hollywood, CA 1973-1975 Graduate Research Assistant, UCLA 1974-1991 Member of Technical Staff, Jet Propulsion Laboratory 1991-1998 Senior Member of Technical Staff, Jet Propulsion Laboratory 1998-2002 Senior Research Scientist, Jet Propulsion Laboratory 2002-present Senior Research Scientist, Space Science Institute Appointments: 1976 Member of Faculty of NATO Advanced Study Institute on Origin of the Solar System, Newcastle upon Tyne 1977-1978 Guest Investigator, Hale Observatories 1978 Visiting Assoc. Prof. of Physics, University of Calif. at Santa Barbara 1978-1980 Executive Committee, Division on Dynamical Astronomy of AAS 1979 Visiting Assoc. Prof. of Earth and Space Science, UCLA 1980 Guest Investigator, Hale Observatories 1983-1984 Guest Investigator, Lowell Observatory 1983-1985 Lunar and Planetary Review Panel (NASA) 1983-1992 Supervisor, Earth and Planetary Physics Group, JPL 1984 Science W.G. for Voyager II Uranus/Neptune Encounters (JPL/NASA) 1984-present Advisor of students in Caltech Summer Undergraduate Research Fellowship Program 1984-1985 ESA/NASA Science Advisory Group for Primitive Bodies Missions 1985-1993 ESA/NASA Comet Nucleus Sample Return Science Definition Team (Deputy Chairman, U.S. -

Jupitor's Great Red Spot
GREAT RED SPOT appears somewhat orange in this remarkably ly ranged from '.'full gray" and "pinkish" to "brick red" and "car· detailed photograph made at the Lunar and Planetary Laboratory mine." The photograph was made on December 23, 1966, by Alika of the University of Arizona. During the century or so that Jupiter's Herring and John Fountain, who used a 61·inch reflecting tele· great red spot bas been closely observed its color has reported. scope. The exposure was one second on High Speed Ektachrome. © 1968 SCIENTIFIC AMERICAN, INC JUPITER'S GREAT RED SPOT There is evidence to suggest that this peculiar Inarking is the top of a "Taylor cohunn": a stagnant region above a bll111p 01' depression at the botton1 of a circulating fluid by Haymond Hide he surface markings of the plan To explain the fluctuations in the red tals suspended in an atmosphere that is Tets have always had a special fas spot's period of rotation one must assume mainly hydrogen admixed with water cination, and no single marking that there are forces acting on the solid and perhaps methane and helium. Other has been more fascinating and puzzling planet capable of causing an equivalent lines of evidence, particularly the fact than the great red spot of Jupiter. Un change in its rotation period. In other that Jupiter's density is only 1.3 times like the elusive "canals" of Mars, the red words, the fluctuations in the rotation the density of water, suggest that the spot unmistakably exists. Although it has period of the red spot are to be regarded main constituents of the planet are hy been known to fade and change color, it as a true reflection of the rotation period drogen and helium. -

Asteroid Regolith Weathering: a Large-Scale Observational Investigation
University of Tennessee, Knoxville TRACE: Tennessee Research and Creative Exchange Doctoral Dissertations Graduate School 5-2019 Asteroid Regolith Weathering: A Large-Scale Observational Investigation Eric Michael MacLennan University of Tennessee, [email protected] Follow this and additional works at: https://trace.tennessee.edu/utk_graddiss Recommended Citation MacLennan, Eric Michael, "Asteroid Regolith Weathering: A Large-Scale Observational Investigation. " PhD diss., University of Tennessee, 2019. https://trace.tennessee.edu/utk_graddiss/5467 This Dissertation is brought to you for free and open access by the Graduate School at TRACE: Tennessee Research and Creative Exchange. It has been accepted for inclusion in Doctoral Dissertations by an authorized administrator of TRACE: Tennessee Research and Creative Exchange. For more information, please contact [email protected]. To the Graduate Council: I am submitting herewith a dissertation written by Eric Michael MacLennan entitled "Asteroid Regolith Weathering: A Large-Scale Observational Investigation." I have examined the final electronic copy of this dissertation for form and content and recommend that it be accepted in partial fulfillment of the equirr ements for the degree of Doctor of Philosophy, with a major in Geology. Joshua P. Emery, Major Professor We have read this dissertation and recommend its acceptance: Jeffrey E. Moersch, Harry Y. McSween Jr., Liem T. Tran Accepted for the Council: Dixie L. Thompson Vice Provost and Dean of the Graduate School (Original signatures are on file with official studentecor r ds.) Asteroid Regolith Weathering: A Large-Scale Observational Investigation A Dissertation Presented for the Doctor of Philosophy Degree The University of Tennessee, Knoxville Eric Michael MacLennan May 2019 © by Eric Michael MacLennan, 2019 All Rights Reserved. -

SPITZER SPACE TELESCOPE MID-IR LIGHT CURVES of NEPTUNE John Stauffer1, Mark S
The Astronomical Journal, 152:142 (8pp), 2016 November doi:10.3847/0004-6256/152/5/142 © 2016. The American Astronomical Society. All rights reserved. SPITZER SPACE TELESCOPE MID-IR LIGHT CURVES OF NEPTUNE John Stauffer1, Mark S. Marley2, John E. Gizis3, Luisa Rebull1,4, Sean J. Carey1, Jessica Krick1, James G. Ingalls1, Patrick Lowrance1, William Glaccum1, J. Davy Kirkpatrick5, Amy A. Simon6, and Michael H. Wong7 1 Spitzer Science Center (SSC), California Institute of Technology, Pasadena, CA 91125, USA 2 NASA Ames Research Center, Space Sciences and Astrobiology Division, MS245-3, Moffett Field, CA 94035, USA 3 Department of Physics and Astronomy, University of Delaware, Newark, DE 19716, USA 4 Infrared Science Archive (IRSA), 1200 E. California Boulevard, MS 314-6, California Institute of Technology, Pasadena, CA 91125, USA 5 Infrared Processing and Analysis Center, MS 100-22, California Institute of Technology, Pasadena, CA 91125, USA 6 NASA Goddard Space Flight Center, Solar System Exploration Division (690.0), 8800 Greenbelt Road, Greenbelt, MD 20771, USA 7 University of California, Department of Astronomy, Berkeley CA 94720-3411, USA Received 2016 July 13; revised 2016 August 12; accepted 2016 August 15; published 2016 October 27 ABSTRACT We have used the Spitzer Space Telescope in 2016 February to obtain high cadence, high signal-to-noise, 17 hr duration light curves of Neptune at 3.6 and 4.5 μm. The light curve duration was chosen to correspond to the rotation period of Neptune. Both light curves are slowly varying with time, with full amplitudes of 1.1 mag at 3.6 μm and 0.6 mag at 4.5 μm. -

Mercury Friday, February 23
ASTRONOMY 161 Introduction to Solar System Astronomy Class 18 Mercury Friday, February 23 Mercury: Basic characteristics Mass = 3.302×1023 kg (0.055 Earth) Radius = 2,440 km (0.383 Earth) Density = 5,427 kg/m³ Sidereal rotation period = 58.6462 d Albedo = 0.11 (Earth = 0.39) Average distance from Sun = 0.387 A.U. Mercury: Key Concepts (1) Mercury has a 3-to-2 spin-orbit coupling (not synchronous rotation). (2) Mercury has no permanent atmosphere because it is too hot. (3) Like the Moon, Mercury has cratered highlands and smooth plains. (4) Mercury has an extremely large iron-rich core. (1) Mercury has a 3-to-2 spin-orbit coupling (not synchronous rotation). Mercury is hard to observe from the Earth (because it is so close to the Sun). Its rotation speed can be found from Doppler shift of radar signals. Mercury’s unusual orbit Orbital period = 87.969 days Rotation period = 58.646 days = (2/3) x 87.969 days Mercury is NOT in synchronous rotation (1 rotation per orbit). Instead, it has 3-to-2 spin-orbit coupling (3 rotations for 2 orbits). Synchronous rotation (WRONG!) 3-to-2 spin-orbit coupling (RIGHT!) Time between one noon and the next is 176 days. Sun is above the horizon for 88 days at the time. Daytime temperatures reach as high as: 700 Kelvin (800 degrees F). Nighttime temperatures drops as low as: 100 Kelvin (-270 degrees F). (2) Mercury has no permanent atmosphere because it is too hot (and has low escape speed). Temperature is a measure of the 3kT v = random speed of m atoms (or v typical speed of atom molecules).