DOCSLIB.ORG

Basic Digital Audio Effects

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Basic Digital Audio Effects Digital Audio Effects Having learned to make basic waveforms and basic filtering lets CM0268 see how we can add some digital audio effects. These may be applied: MATLAB DSP GRAPHICS As part of the audio creation/synthesis stage — to be subsequently 332 • filtered, (re)synthesised At the end of the audio chain — as part of the production/mastering • phase. Effects can be applied in different orders and sometimes in a • parallel audio chain. The order of applying the same effects can have drastic differences 1 • in the output audio. Selection of effects and the ordering is a matter for the sound you JJ • wish to create. There is no absolute rule for the ordering. II J I Back Close Effect Types and Parameters Effect Types and Parameters IPATCH LEVEL Typical Guitar (and other) Effects Pipeline PATCH LEVEL (Prm) illustration below. You can use all effect Determines the overall volume level of the patch. SomeLinking ordering Effects is standard for some audiomodule processing,s together or seE.glecti:vely set certain 2 1 0 Sets the patch level in the range from 2 – 98, 1.0. A setting of 80 corresponds to unity gain (input level Compression Distortion EQ modulesNoise to on Redux or off. Amp Sim and output level are equal). The patches of the! G1/G1X consist of! eight ! ! ! Modulation Delay Reverb CM0268 serially linked effect modules, as shown in the MATLAB ! ! DSP ICOMP/EFX (Compressor/EFX) module GRAPHICS Common for some guitar effects pedal: This module comprises the effects that control the level dynamics such as compressor, and Effect modules 333 modulation effects such as tremolo and phaser. COMP/EFX DRIVE EQ ZNR AMP MODULATION DELAY REVERB COMP/EFX (Type&Prm) Compressor FD Clean ZNR AMP Sim. Chorus Delay Hall Auto Wah VX Clean Ensemble Tape Echo Room Adjusts the COMP/EFX module effect type and intensity. Booster HW Clean Flanger Analog Spring Delay Compressor Tremolo US Blues Step Arena Ping Pong C 1 C 9 This is an MXR Dynacomp type compressor. It attenuates high-level signal components and boosts Phaser BG Crunch Pitch Shift Delay Tiled Room low-level signal components, to keep the overall signal level within a certain range. Higher setting values result in higher sensitivity. Effect types Auto Wah A 1 A 9 This effect varies wah in accordance with picking intensity. Higher setting values result in higher * Manufacturer names and product names mentioned in this listing are trademarks or 1 sensitivity. registered trademarks of their respective owners. The names are used only to illustrate sonic B 1 B 9 Booster characteristics and do not indicate any affiliation with ZOOM CORPORATION. Raises signal level and creates a dynamic sound. Higher setting values result in higher gain. JJ T 1 T 9 Tremolo For some effect modules, you can select an effect type from several possible choices. For example, the II This effect periodically varies the volume. Higher setting values result in faster modulation rate. MODULATION module comprises Chorus, Flanger, and other effect types. The REVERB module J Phaser comprises Hall, Room, and other effect types from which you can choose one. P 1 P 9 This effect produces sound with a pulsating character. Higher setting values result in faster modulation Note: Other Effects Units allow for a completely reconfigurable I rate. effects pipeline. E.g. Boss GT-8 Back Ring Mod (Ring Modulator) R 1 R 9 This effect produces a metallic ringing sound. Higher setting values result in higher modulation G Tap Close frequency. Explanation of symbols A [TAP] icon in the listing Slow Attack TAP indicates a parameter that can be S 1 S 9 This effect reduces the attack rate of each individual note, producing a violin playing style sound. Higher setting values result in slower attack times. G Module selector set with the [BANK UP•TAP] Vox Wah The Module selector symbol key. V 1 V 9 This effect simulates a half-open vintage VOX wah pedal. Higher setting values result in higher shows the position of the knob at emphasized frequency. When the respective module/effect type is which this module/parameter is Cry Wah selected in edit mode and the [BANK UP•TAP] called up. 1 9 This effect simulates a half-open vintage Crybaby wah pedal. Higher setting values result in higher key is pressed repeatedly, the parameter (such as emphasized frequency. G Expression pedal modulation rate or delay time) will be set according to the interval in which the key is A pedal icon in the listing IDRIVE module pressed. indicates a parameter that can be This module includes 20 types of distortion and an acoustic simulator. For this module, the two controlled with the built-in or an items DRIVE and GAIN can be adjusted separately. external expression pedal. DRIVE (Type) Selects the effect type for the DRIVE module. When this item is selected, the parameter in the module can then be controlled in real time with a FD Clean VX Clean connected expression pedal. Clean sound of a Fender Twin Reverb ('65 F D V Clean sound of the combo amp VOX AC- model) favored by guitarists of many 30 operating in class A. music styles. 18 ZOOM G1/G1X ZOOM G1/G1X 19 Classifying Effects Audio effects can be classified by the way do their processing: CM0268 MATLAB DSP Basic Filtering — Lowpass, Highpass filter etc,, Equaliser GRAPHICS Time Varying Filters — Wah-wah, Phaser 334 Delays — Vibrato, Flanger, Chorus, Echo Modulators — Ring modulation, Tremolo, Vibrato Non-linear Processing — Compression, Limiters, Distortion, Exciters/Enhancers Spacial Effects — Panning, Reverb, Surround Sound 1 JJ II J I Back Close Basic Digital Audio Filtering Effects: Equalisers CM0268 MATLAB DSP GRAPHICS Filters by definition remove/attenuate audio from the spectrum 335 above or below some cut-off frequency. For many audio applications this a little too restrictive • Equalisers, by contrast, enhance/diminish certain frequency bands whilst leaving others unchanged: 1 Built using a series of shelving and peak filters • First or second-order filters usually employed. • JJ II J I Back Close Shelving and Peak Filters Shelving Filter — Boost or cut the low or high frequency bands with CM0268 a cut-off frequency, Fc and gain G MATLAB DSP GRAPHICS 336 Peak Filter — Boost or cut mid-frequency bands with a cut-off frequency, Fc, a bandwidth, fb and gain G 1 JJ II J I Back Close Shelving Filters A first-order shelving filter may be described by the transfer function: CM0268 MATLAB DSP H0 GRAPHICS H(z) = 1 + (1 A(z)) where LF=HF + = 2 ± − 337 where A(z) is a first-order allpass filter — passes all frequencies but modifies phase: 1 z− + a A z B=C ( ) = 1 B=Boost, C=Cut 1 + aB=Cz− which leads the following algorithm/difference equation: 1 y (n) = a x(n) + x(n 1) a y (n 1) 1 B=C − − B=C 1 − JJ H0 II y(n) = (x(n) y (n)) + x(n) 2 ± 1 J I Back Close Shelving Filters (Cont.) The gain, G, in dB can be adjusted accordingly: CM0268 G=20 MATLAB H = V 1 where V = 10 DSP 0 0 − 0 GRAPHICS 338 and the cut-off frequency for boost, aB, or cut, aC are given by: tan(2πfc=fs) 1 aB = − tan(2πfc=fs) + 1 1 tan(2πfc=fs) V0 aC = − tan(2πfc=fs) V0 − JJ II J I Back Close Shelving Filters Signal Flow Graph H0/2 x(n) A(z) y (n) y(n) CM0268 1 + MATLAB DSP ±× GRAPHICS 339 where A(z) is given by: x(n 1) x(n) T − aB/C 1 ×× y(n) 1 ++ JJ aB/C × − II J T y (n 1) I 1 − Back Close 1 1 Peak Filters A first-order shelving filter may be described by the transfer function: CM0268 MATLAB DSP H0 GRAPHICS H(z) = 1 + (1 A2(z)) 2 − 340 where A2(z) is a second-order allpass filter: 1 2 a + (d da )z− + z− A(z) = − B − B 1 + (d da )z 1 + a z 2 − B − B − which leads the following algorithm/difference equation: 1 y (n) = 1a x(n) + d(1 a )x(n 1) + x(n 2) 1 B=C − B=C − − d(1 aB=C)y1(n 1) + aB=Cy1(n 2) JJ − − − − H II y(n) = 0 (x(n) y (n)) + x(n) 2 − 1 J I Back Close Peak Filters (Cont.) The center/cut-off frequency, d, is given by: d = cos(2πf =f ) c s CM0268 − MATLAB DSP GRAPHICS The H0 by relation to the gain, G, as before: 341 H = V 1 where V = 10G=20 0 0 − 0 and the bandwidth, fb is given by the limits for boost, aB, or cut, aC are given by: 1 tan(2πfb=fs) 1 aB = − JJ tan(2πf =f ) + 1 b s II tan(2πfb=fs) V0 aC = − J tan(2πfb=fs) V0 I − Back Close Peak Filters Signal Flow Graph 1 H0/2 − x(n) A(z) y1(n) y(n) CM0268 + + MATLAB DSP ×× GRAPHICS 342 where A(z) is given by: x(n) x(n 1) x(n 2) − − TT aB/C d(1 aB/C ) 1 ×××− − y(n) 1 +++ aB/C d(1 aB/C ) JJ ××− − II J TT y (n 2) y (n 1) 1 − 1 − I Back Close 1 1 Shelving Filter EQ MATLAB Example The following function, shelving.m performs a shelving filter: CM0268 MATLAB function [b, a] = shelving(G, fc, fs, Q, type) DSP % GRAPHICS % Derive coefficients for a shelving filter with a given amplitude 343 % and cutoff frequency. All coefficients are calculated as % described in Zolzer’s DAFX book (p.
Load more

Recommended publications
  • Gemini Chorus User's Guide
    Gemini Chorus User’s Guide Welcome Thank you for purchasing the Gemini Chorus. This powerful stereo effects pedal features a collection of meticulously crafted chorus sounds ranging from classic dual-voice sounds to lush quad-voice ensembles. With a simple control set, the Gemini can work in a wide variety of musical settings, and the powerful MIDI and Neuro control options under the hood provide access to a vast array of additional tonal possibilities. The Gemini is housed in a durable, lightweight aluminum housing, packing rack mount power and flexibility into a compact, easy-to-use stompbox. SA242 Gemini Chorus User’s Guide 1 The USB and Neuro ports transform the Gemini from a simple chorus pedal into a powerful multi- effects unit. Using the free Neuro App (iOS and Android), a wide range of additional control parameters and effect types (phaser, flanger, resonator) are accessible. When used together with the Neuro Hub, the Gemini is fully MIDI-controllable and 128 multi-pedal presets, or “scenes,” can be saved for instant recall on the stage or in the studio. The Gemini can also connect directly to a passive expression pedal or the Hot Hand for expressive control of any parameter. The Quick Start guide will help you with the basics. For more in-depth information about the Gemini Chorus, move on to the following sections, starting with Connections. Enjoy! - The Source Audio Team Overview Diverse Chorus Sounds – Choose from traditional chorus tones such as Dual, Classic, and Quad, or delve deeper into unique sounds cooked up in the Source Audio lab.
    [Show full text]
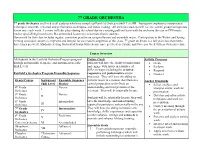
  • 7Th GRADE ORCHESTRA 7Th Grade Orchestra Is Offered to All Students Who Have Completed Fairfield Orchestra Skill Level III
    7th GRADE ORCHESTRA 7th grade Orchestra is offered to all students who have completed Fairfield Orchestra Skill Level III. Instruction emphasizes instrumental techniques, ensemble rehearsal and performance techniques, and music reading. All orchestra students will receive a small group homogenous lesson once each week. Lessons will take place during the school day on a rotating pull-out basis with the orchestra director or FPS music teacher specializing in orchestra. Recommended lesson size is no more than 6 students. Homework for this class includes regular, consistent practice on assigned lesson and ensemble music. Participation in the Winter and Spring evening curricular concerts is expected and integral for successful completion of this class. 7th grade orchestra is a full year class that meets three times per week. Students electing Orchestra/Chorus will rehearse once per week in Chorus, and twice per week with an Orchestra class. Course Overview All students in the Fairfield Orchestra Program progress Course Goals Artistic Processes through an Ensemble Sequence and instrument specific Students will have the ability to understand • Create Skill Levels. and engage with music in a number of • Perform different ways, including the creative, • Respond Fairfield’s Orchestra Program Ensemble Sequence responsive and performative artistic • Connect processes. They will have the ability to Grade/Course Instrument Ensemble Sequence perform music in a manner that illustrates Anchor Standards Skill Level Marker careful preparation and reflects an • Select, analyze, and 4th Grade Novice understanding and interpretation of the I interpret artistic work for Orchestra selection. They will be musically literate. presentation. 5th Grade Novice II • Develop and refine artistic Orchestra Students will be artistically literate: they will techniques and work for th 6 Grade Intermediate have the knowledge and understanding presentation.
    [Show full text]
  • UC Riverside UC Riverside Electronic Theses and Dissertations
    UC Riverside UC Riverside Electronic Theses and Dissertations Title Sonic Retro-Futures: Musical Nostalgia as Revolution in Post-1960s American Literature, Film and Technoculture Permalink https://escholarship.org/uc/item/65f2825x Author Young, Mark Thomas Publication Date 2015 Peer reviewed|Thesis/dissertation eScholarship.org Powered by the California Digital Library University of California UNIVERSITY OF CALIFORNIA RIVERSIDE Sonic Retro-Futures: Musical Nostalgia as Revolution in Post-1960s American Literature, Film and Technoculture A Dissertation submitted in partial satisfaction of the requirements for the degree of Doctor of Philosophy in English by Mark Thomas Young June 2015 Dissertation Committee: Dr. Sherryl Vint, Chairperson Dr. Steven Gould Axelrod Dr. Tom Lutz Copyright by Mark Thomas Young 2015 The Dissertation of Mark Thomas Young is approved: Committee Chairperson University of California, Riverside ACKNOWLEDGEMENTS As there are many midwives to an “individual” success, I’d like to thank the various mentors, colleagues, organizations, friends, and family members who have supported me through the stages of conception, drafting, revision, and completion of this project. Perhaps the most important influences on my early thinking about this topic came from Paweł Frelik and Larry McCaffery, with whom I shared a rousing desert hike in the foothills of Borrego Springs. After an evening of food, drink, and lively exchange, I had the long-overdue epiphany to channel my training in musical performance more directly into my academic pursuits. The early support, friendship, and collegiality of these two had a tremendously positive effect on the arc of my scholarship; knowing they believed in the project helped me pencil its first sketchy contours—and ultimately see it through to the end.
    [Show full text]
  • Frank Zappa and His Conception of Civilization Phaze Iii
    University of Kentucky UKnowledge Theses and Dissertations--Music Music 2018 FRANK ZAPPA AND HIS CONCEPTION OF CIVILIZATION PHAZE III Jeffrey Daniel Jones University of Kentucky, [email protected] Digital Object Identifier: https://doi.org/10.13023/ETD.2018.031 Right click to open a feedback form in a new tab to let us know how this document benefits ou.y Recommended Citation Jones, Jeffrey Daniel, "FRANK ZAPPA AND HIS CONCEPTION OF CIVILIZATION PHAZE III" (2018). Theses and Dissertations--Music. 108. https://uknowledge.uky.edu/music_etds/108 This Doctoral Dissertation is brought to you for free and open access by the Music at UKnowledge. It has been accepted for inclusion in Theses and Dissertations--Music by an authorized administrator of UKnowledge. For more information, please contact [email protected]. STUDENT AGREEMENT: I represent that my thesis or dissertation and abstract are my original work. Proper attribution has been given to all outside sources. I understand that I am solely responsible for obtaining any needed copyright permissions. I have obtained needed written permission statement(s) from the owner(s) of each third-party copyrighted matter to be included in my work, allowing electronic distribution (if such use is not permitted by the fair use doctrine) which will be submitted to UKnowledge as Additional File. I hereby grant to The University of Kentucky and its agents the irrevocable, non-exclusive, and royalty-free license to archive and make accessible my work in whole or in part in all forms of media, now or hereafter known. I agree that the document mentioned above may be made available immediately for worldwide access unless an embargo applies.
    [Show full text]
  • Metaflanger Table of Contents
    MetaFlanger Table of Contents Chapter 1 Introduction 2 Chapter 2 Quick Start 3 Flanger effects 5 Chorus effects 5 Producing a phaser effect 5 Chapter 3 More About Flanging 7 Chapter 4 Controls & Displa ys 11 Section 1: Mix, Feedback and Filter controls 11 Section 2: Delay, Rate and Depth controls 14 Section 3: Waveform, Modulation Display and Stereo controls 16 Section 4: Output level 18 Chapter 5 Frequently Asked Questions 19 Chapter 6 Block Diagram 20 Chapter 7.........................................................Tempo Sync in V5.0.............22 MetaFlanger Manual 1 Chapter 1 - Introduction Thanks for buying Waves processors. MetaFlanger is an audio plug-in that can be used to produce a variety of classic tape flanging, vintage phas- er emulation, chorusing, and some unexpected effects. It can emulate traditional analog flangers,fill out a simple sound, create intricate harmonic textures and even generate small rough reverbs and effects. The following pages explain how to use MetaFlanger. MetaFlanger’s Graphic Interface 2 MetaFlanger Manual Chapter 2 - Quick Start For mixing, you can use MetaFlanger as a direct insert and control the amount of flanging with the Mix control. Some applications also offer sends and returns; either way works quite well. 1 When you insert MetaFlanger, it will open with the default settings (click on the Reset button to reload these!). These settings produce a basic classic flanging effect that’s easily tweaked. 2 Preview your audio signal by clicking the Preview button. If you are using a real-time system (such as TDM, VST, or MAS), press ‘play’. You’ll hear the flanged signal.
    [Show full text]
  • Neural Modelling of Periodically Modulated Time-Varying Effects
    Proceedings of the 23rd International Conference on Digital Audio Effects (DAFx2020),(DAFx-20), Vienna, Vienna, Austria, Austria, September September 8–12, 2020-21 2020 NEURAL MODELLING OF PERIODICALLY MODULATED TIME-VARYING EFFECTS Alec Wright and Vesa Välimäki ∗ Acoustics Lab, Dept. of Signal Processing and Acoustics Aalto University Espoo, Finland [email protected] ABSTRACT In recent years, numerous studies on virtual analog modelling of guitar amplifiers [11, 12, 13, 14, 4, 15] and other nonlinear sys- This paper proposes a grey-box neural network based approach tems [16, 17] using neural networks have been published. Neural to modelling LFO modulated time-varying effects. The neural network modelling of time-varying audio effects has received less network model receives both the unprocessed audio, as well as attention, with the first publications being published over the past the LFO signal, as input. This allows complete control over the year [18, 3]. Whilst Martínez et al. report that accurate emulations model’s LFO frequency and shape. The neural networks are trained of several time-varying effects were achieved, the model utilises using guitar audio, which has to be processed by the target effect bi-directional Long Short Term Memory (LSTM) and is therefore and also annotated with the predicted LFO signal before training. non-causal and unsuitable for real-time applications. A measurement signal based on regularly spaced chirps was used In this paper we present a general approach for real-time mod- to accurately predict the LFO signal. The model architecture has elling of audio effects with parameters that are modulated by a been previously shown to be capable of running in real-time on a Low Frequency Oscillator (LFO) signal.
    [Show full text]
  • Zoom Handy Recorder App Operations Manual (13 MB Pdf)
    ver. 2.0 Operation Manual © 2014 ZOOM CORPORATION Copying or reproduction of this document in whole or in part without permission is prohibited. Contents Introduction‥ ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥ 3 Copyrights‥ ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥ 3 Main Screen ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥ 4 Landscape mode (new in ver. 2.0)‥ ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥ 5 Recording‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥ 6 Pausing recording‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥ 6 Adjusting the recording level‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥ 7 Setting the recording format‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥ 7 Muting the input‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥ 8 Adding recordings (landscape mode only) (new in ver. 2.0)‥ ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥ 9 Using mid-side recording ( series MS mic only feature)‥ ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥ 11 Setting mid-side monitoring‥ ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥ 11 Playback‥ ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥ 12 Selecting‥and‥playing‥files‥ ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥ 12 Pausing playback‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥ 13 Playing‥files‥from‥the‥FILE‥screen‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥ 13 Adjusting the playback level‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥ 14 Repeating playback of an interval (new in ver. 2.0) ‥ ‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥ 14 Editing‥and‥deleting‥files‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥ 15 Dividing‥files‥(landscape‥mode‥only)‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥
    [Show full text]
  • Pipa by Moshe Denburg.Pdf
    Pipa • Pipa [ Picture of Pipa ] Description A pear shaped lute with 4 strings and 19 to 30 frets, it was introduced into China in the 4th century AD. The Pipa has become a prominent Chinese instrument used for instrumental music as well as accompaniment to a variety of song genres. It has a ringing ('bass-banjo' like) sound which articulates melodies and rhythms wonderfully and is capable of a wide variety of techniques and ornaments. Tuning The pipa is tuned, from highest (string #1) to lowest (string #4): a - e - d - A. In piano notation these notes correspond to: A37 - E 32 - D30 - A25 (where A37 is the A below middle C). Scordatura As with many stringed instruments, scordatura may be possible, but one needs to consult with the musician about it. Use of a capo is not part of the pipa tradition, though one may inquire as to its efficacy. Pipa Notation One can utilize western notation or Chinese. If western notation is utilized, many, if not all, Chinese musicians will annotate the music in Chinese notation, since this is their first choice. It may work well for the composer to notate in the western 5 line staff and add the Chinese numbers to it for them. This may be laborious, and it is not necessary for Chinese musicians, who are quite adept at both systems. In western notation one writes for the Pipa at pitch, utilizing the bass and treble clefs. In Chinese notation one utilizes the French Chevé number system (see entry: Chinese Notation). In traditional pipa notation there are many symbols that are utilized to call for specific techniques.
    [Show full text]
  • Estimation of Direction of Arrival of Acoustic Signals Using Microphone
    Time-Delay-Estimate Based Direction-of-Arrival Estimation for Speech in Reverberant Environments by Krishnaraj Varma Thesis submitted to the Faculty of The Bradley Department of Electrical and Computer Engineering Virginia Polytechnic Institute and State University in partial fulfillment of the requirements for the degree of Master of Science in Electrical Engineering APPROVED Dr. A. A. (Louis) Beex, Chairman Dr. Ira Jacobs Dr. Douglas K. Lindner October 2002 Blacksburg, VA KEYWORDS: Microphone array processing, Beamformer, MUSIC, GCC, PHAT, SRP-PHAT, TDE, Least squares estimate © 2002 by Krishnaraj Varma Time-Delay-Estimate Based Direction-of-Arrival Estimation for Speech in Reverberant Environments by Krishnaraj Varma Dr. A. A. (Louis) Beex, Chairman The Bradley Department of Electrical and Computer Engineering (Abstract) Time delay estimation (TDE)-based algorithms for estimation of direction of arrival (DOA) have been most popular for use with speech signals. This is due to their simplicity and low computational requirements. Though other algorithms, like the steered response power with phase transform (SRP-PHAT), are available that perform better than TDE based algorithms, the huge computational load required for this algorithm makes it unsuitable for applications that require fast refresh rates using short frames. In addition, the estimation errors that do occur with SRP-PHAT tend to be large. This kind of performance is unsuitable for an application such as video camera steering, which is much less tolerant to large errors than it is to small errors. We propose an improved TDE-based DOA estimation algorithm called time delay selection (TIDES) based on either minimizing the weighted least squares error (MWLSE) or minimizing the time delay separation (MWTDS).
    [Show full text]
  • 21065L Audio Tutorial
    a Using The Low-Cost, High Performance ADSP-21065L Digital Signal Processor For Digital Audio Applications Revision 1.0 - 12/4/98 dB +12 0 -12 Left Right Left EQ Right EQ Pan L R L R L R L R L R L R L R L R 1 2 3 4 5 6 7 8 Mic High Line L R Mid Play Back Bass CNTR 0 0 3 4 Input Gain P F R Master Vol. 1 2 3 4 5 6 7 8 Authors: John Tomarakos Dan Ledger Analog Devices DSP Applications 1 Using The Low Cost, High Performance ADSP-21065L Digital Signal Processor For Digital Audio Applications Dan Ledger and John Tomarakos DSP Applications Group, Analog Devices, Norwood, MA 02062, USA This document examines desirable DSP features to consider for implementation of real time audio applications, and also offers programming techniques to create DSP algorithms found in today's professional and consumer audio equipment. Part One will begin with a discussion of important audio processor-specific characteristics such as speed, cost, data word length, floating-point vs. fixed-point arithmetic, double-precision vs. single-precision data, I/O capabilities, and dynamic range/SNR capabilities. Comparisions between DSP's and audio decoders that are targeted for consumer/professional audio applications will be shown. Part Two will cover example algorithmic building blocks that can be used to implement many DSP audio algorithms using the ADSP-21065L including: Basic audio signal manipulation, filtering/digital parametric equalization, digital audio effects and sound synthesis techniques. TABLE OF CONTENTS 0. INTRODUCTION ................................................................................................................................................................4 1.
    [Show full text]
  • TA-1VP Vocal Processor
    D01141720C TA-1VP Vocal Processor OWNER'S MANUAL IMPORTANT SAFETY PRECAUTIONS ªª For European Customers CE Marking Information a) Applicable electromagnetic environment: E4 b) Peak inrush current: 5 A CAUTION: TO REDUCE THE RISK OF ELECTRIC SHOCK, DO NOT REMOVE COVER (OR BACK). NO USER- Disposal of electrical and electronic equipment SERVICEABLE PARTS INSIDE. REFER SERVICING TO (a) All electrical and electronic equipment should be QUALIFIED SERVICE PERSONNEL. disposed of separately from the municipal waste stream via collection facilities designated by the government or local authorities. The lightning flash with arrowhead symbol, within equilateral triangle, is intended to (b) By disposing of electrical and electronic equipment alert the user to the presence of uninsulated correctly, you will help save valuable resources and “dangerous voltage” within the product’s prevent any potential negative effects on human enclosure that may be of sufficient health and the environment. magnitude to constitute a risk of electric (c) Improper disposal of waste electrical and electronic shock to persons. equipment can have serious effects on the The exclamation point within an equilateral environment and human health because of the triangle is intended to alert the user to presence of hazardous substances in the equipment. the presence of important operating and (d) The Waste Electrical and Electronic Equipment (WEEE) maintenance (servicing) instructions in the literature accompanying the appliance. symbol, which shows a wheeled bin that has been crossed out, indicates that electrical and electronic equipment must be collected and disposed of WARNING: TO PREVENT FIRE OR SHOCK separately from household waste. HAZARD, DO NOT EXPOSE THIS APPLIANCE TO RAIN OR MOISTURE.
    [Show full text]
  • Common Tape Manipulation Techniques and How They Relate to Modern Electronic Music
    Common Tape Manipulation Techniques and How They Relate to Modern Electronic Music Matthew A. Bardin Experimental Music & Digital Media Center for Computation & Technology Louisiana State University Baton Rouge, Louisiana 70803 [email protected] ABSTRACT the 'play head' was utilized to reverse the process and gen- The purpose of this paper is to provide a historical context erate the output's audio signal [8]. Looking at figure 1, from to some of the common schools of thought in regards to museumofmagneticsoundrecording.org (Accessed: 03/20/2020), tape composition present in the later half of the 20th cen- the locations of the heads can be noticed beneath the rect- tury. Following this, the author then discusses a variety of angular protective cover showing the machine's model in the more common techniques utilized to create these and the middle of the hardware. Previous to the development other styles of music in detail as well as provides examples of the reel-to-reel machine, electronic music was only achiev- of various tracks in order to show each technique in process. able through live performances on instruments such as the In the following sections, the author then discusses some of Theremin and other early predecessors to the modern syn- the limitations of tape composition technologies and prac- thesizer. [11, p. 173] tices. Finally, the author puts the concepts discussed into a modern historical context by comparing the aspects of tape composition of the 20th century discussed previous to the composition done in Digital Audio recording and manipu- lation practices of the 21st century. Author Keywords tape, manipulation, history, hardware, software, music, ex- amples, analog, digital 1.
    [Show full text]