A Multiscale Diffuse-Interface Model for Two-Phase Flow in Porous Media
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Wettability As Related to Capillary Action in Porous Media
Wettability as Related to Capillary Action in Porous l\1edia SOCONY MOBIL OIL CO. JAMES C. MELROSE DALLAS, TEX. ABSTRACT interpreted with the aid of a model employing the concept of a cylindrical capillary tube. This The contact angle is one of the boundary approach has enjoyed a certain degree of success Downloaded from http://onepetro.org/spejournal/article-pdf/5/03/259/2153830/spe-1085-pa.pdf by guest on 26 September 2021 conditions for the differential equation specifying in correlating experimental results. 13 The general the configuration of fluid-fluid interfaces. Hence, ization of this model, however, to situations which applying knowledge concerning the wettability of a involve varying wettability, has not been established solid surface to problems of fluid distribution in and, in fact, is likely to be unsuccessful. porous solids, it is important to consider the In this paper another approach to this problem complexity of the geometrical shapes of the indi will be discussed. A considerable literature relating vidual, interconnected pores. to this approach exists in the field of soil science, As an approach to this problem, the ideal soil where it is referred to as the ideal soil model. model introduced by soil physicists is discussed Certain features of this model have also been in detail. This model predicts that the pore structure discussed by Purcell14 in relation to variable of typical porous solids will lead to hysteresis wettability. The application of this model, however, effects in capillary pressure, even if a zero value to studying the role of wettability in capillary of the contact angle is maintained. -

Capillary Action in Celery Carpet Again and See If You Can the Leaf Is in the Sun
Walking Water: Set aside the supplies you will need which are the 5 plastic cups (or 5 glasses or Go deeper and get scientific and test the differences between jars you may have), the three vials of food coloring (red, yellow & blue) and 4 the different types of paper towels you have in your kit (3), sheets of the same type of paper towel. You will also need time for this demo to the different food colorings and different levels of water in develop. your glass. Follow the directions here to wrap up your Fold each of the 4 paper towels lengthwise about 4 times so that you have nice understanding of capillary action: long strips. Line your five cups, glasses or jars up in a line or an arc or a circle. Fill the 1st, 3rd, and 5th cup about 1/3 to ½ full with tap water. Leave the in-between https://www.whsd.k12.pa.us/userfiles/1587/Classes/74249/c cups empty. Add just a couple or a few drops of food color to the cups with water appilary%20action.pdf – no mixing colors, yet. Put your strips of paper towel into the cups so that one end goes from a wet cup Leaf Transpiration to a dry cup and that all cups are linked by paper towel bridges. Watch the water Bending Water Does water really leave the plant start to wick up the paper. This is capillary action which involves adhesion and Find the balloons in the bags? through the leaves? cohesion properties of water. -

Surface Tension Bernoulli Principle Fluid Flow Pressure
Lecture 9. Fluid flow Pressure Bernoulli Principle Surface Tension Fluid flow Speed of a fluid in a pipe is not the same as the flow rate Depends on the radius of the pipe. example: Low speed Same low speed Large flow rate Small flow rate Relating: Fluid flow rate to Average speed L v is the average speed = L/t A v Volume V =AL A is the area Flow rate Q is the volume flowing per unit time (V/t) Q = (V/t) Q = AL/t = A v Q = A v Flow rate Q is the area times the average speed Fluid flow -- Pressure Pressure in a moving fluid with low viscosity and laminar flow Bernoulli Principle Relates the speed of the fluid to the pressure Speed of a fluid is high—pressure is low Speed of a fluid is low—pressure is high Daniel Bernoulli (Swiss Scientist 1700-1782) Bernoulli Equation 1 Prr v2 gh constant 2 Fluid flow -- Pressure Bernoulli Equation 11 Pr v22 r gh P r v r gh 122 1 1 2 2 2 Fluid flow -- Pressure Bernoulli Principle P1 P2 Fluid v2 v1 if h12 h 11 Prr v22 P v 122 1 2 2 1122 P11r v22 r gh P r v r gh 1rrv 1 v 1 P 2 P 2 2 22222 1 1 2 if v22 is higher then P is lower Fluid flow Venturi Effect –constricted tube enhances the Bernoulli effect P1 P3 P2 A A v1 1 v2 3 v3 A2 If fluid is incompressible flow rate Q is the same everywhere along tube Q = A v A v 1 therefore A1v 1 = A2 2 v2 = v1 A2 Continuity of flow Since A2 < A1 v2 > v1 Thus from Bernoulli’s principle P1 > P2 Fluid flow Bernoulli’s principle: Explanation P1 P2 Fluid Speed increases in smaller tube Therefore kinetic energy increases. -

On the Numerical Study of Capillary-Driven Flow in a 3-D Microchannel Model
Copyright © 2015 Tech Science Press CMES, vol.104, no.4, pp.375-403, 2015 On the Numerical Study of Capillary-driven Flow in a 3-D Microchannel Model C.T. Lee1 and C.C. Lee2 Abstract: In this article, we demonstrate a numerical 3-D chip, and studied the capillary dynamics inside the microchannel. We applied the level set method on the Navier-Stokes equation which incorporates the surface tension and two-phase flow characteristics. We analyzed the capillary dynamics near the junction of two microchannels. Such a highlighting point is important that it not only can provide the information of interface behavior when fluids are made into a head-on collision, but also emphasize the idea for the design of the chip. In addition, we study the pressure distribution of the fluids at the junction. It is shown that the model can produce nearly 2000 Pa pressure difference to help push the water through the microchannel against the air. The nonlinear interaction between capillary flows is recorded. Such a nonlinear phenomenon, to our knowledge, occurs due to the surface tension takes action with the wetted wall boundaries in the channel and the nonlinear governing equations for capillary flow. Keywords: Microchannel, Navier-Stokes equation, Capillary flow, Finite ele- ment analysis, two-phase flow. 1 Introduction Microfluidics system saw the importance of development of the bio-chip, which essentially is a miniaturized laboratory that can perform hundreds or thousands of simultaneous biochemical reactions. However, it is almost impossible to find any instrument to measure or detect the model, in particular, to comprehend the internal flow dynamics for the microchannel model, due to the model has been downsizing to a micro/nano- meter scale. -

Numerical Modeling of Capillary-Driven Flow in Open Microchannels: an Implication of Optimized Wicking Fabric Design
Scholars' Mine Masters Theses Student Theses and Dissertations Summer 2018 Numerical modeling of capillary-driven flow in open microchannels: An implication of optimized wicking fabric design Mehrad Gholizadeh Ansari Follow this and additional works at: https://scholarsmine.mst.edu/masters_theses Part of the Environmental Engineering Commons, Mathematics Commons, and the Mechanical Engineering Commons Department: Recommended Citation Ansari, Mehrad Gholizadeh, "Numerical modeling of capillary-driven flow in open microchannels: An implication of optimized wicking fabric design" (2018). Masters Theses. 7792. https://scholarsmine.mst.edu/masters_theses/7792 This thesis is brought to you by Scholars' Mine, a service of the Missouri S&T Library and Learning Resources. This work is protected by U. S. Copyright Law. Unauthorized use including reproduction for redistribution requires the permission of the copyright holder. For more information, please contact [email protected]. NUMERICAL MODELING OF CAPILLARY-DRIVEN FLOW IN OPEN MICROCHANNELS: AN IMPLICATION OF OPTIMIZED WICKING FABRIC DESIGN by MEHRAD GHOLIZADEH ANSARI A THESIS Presented to the Faculty of the Graduate School of the MISSOURI UNIVERSITY OF SCIENCE AND TECHNOLOGY In Partial Fulfillment of the Requirements for the Degree MASTER OF SCIENCE IN ENVIRONMENTAL ENGINEERING 2018 Approved by Dr. Wen Deng, Advisor Dr. Joseph Smith Dr. Jianmin Wang Dr. Xiong Zhang 2018 Mehrad Gholizadeh Ansari All Rights Reserved iii PUBLICATION THESIS OPTION This thesis has been formatted using the publication option: Paper I, pages 16-52, are intended for submission to the Journal of Computational Physics. iv ABSTRACT The use of microfluidics to transfer fluids without applying any exterior energy source is a promising technology in different fields of science and engineering due to their compactness, simplicity and cost-effective design. -

Capillary Action
UNIT ONE • LESSON EIGHT Pert. 2 Group Discussion • Did you get similar results for the celery and Whet. IP? carnations? • Were there different results for different lengths Ask students: If you could change one thing about Maving Cln Up: of carnations or celery? this investigation to learn something new, what •Where do you think the water goes once it gets would you try? When we change one part of an r===Capillary J\cliian I to the top of the plant? experiment to see how it affects our results, this • What did you learn about water from this ex change is known as a variable. Use the chart in periment? be drawn through the your journal to record your ideas about what might Have you ever wondered • Did everyone have the same results? how water gets from narrow capillary tubes happen if you change some of the variables. Some •What did you like about this investigation? 1.eerning the roots of a tree to inside the plant. For possibilities are: • What variables did you try? capillary action to occur, • Will you get the same results if you use different Clbjecliive& its leaves, or why pa per •What surprised you? towels are able to soak up the attraction between the quantities of water or different amounts of food a soggy spill? It has to do water molecules and the coloring? Students will: The "Why" and The "How" tree molecules (adhesion) • What if you use soapy water? Salty water? Cold with the property of water This investigation illustrates the property of water known as capillary adion. -

A Similarity Parameter for Capillary Flows
INSTITUTE OF PHYSICS PUBLISHING JOURNAL OF PHYSICS D: APPLIED PHYSICS J. Phys. D: Appl. Phys. 36 (2003) 3156–3167 PII: S0022-3727(03)65940-1 A similarity parameter for capillary flows K A Polzin and E Y Choueiri Electric Propulsion and Plasma Dynamics Laboratory (EPPDyL), Mechanical and Aerospace Engineering Department, Princeton University, Princeton, New Jersey 08544, USA E-mail: [email protected] Received 11 July 2003 Published 25 November 2003 Online at stacks.iop.org/JPhysD/36/3156 Abstract A similarity parameter for quasi-steady fluid flows advancing into horizontal capillary channels is presented. This parameter can be interpreted as the ratio of the average fluid velocity in the capillary channel to a characteristic velocity of quasi-steady capillary flows. It allows collapsing a large data set of previously published and recent measurements spanning five orders of magnitude in the fluid velocity, 14 different fluids, and four different geometries onto a single curve and indicates the existence of a universal prescription for such flows. On timescales longer than the characteristic time it takes for the flow to become quasi-steady, the one-dimensional momentum equation leads to a non-dimensional relationship between the similarity parameter and the penetration depth that agrees well with most measurements. Departures from that prescription can be attributed to effects that are not accounted for in the one-dimensional theory. This work is dedicated to Professor Harvey Lam on the occasion of his recovery. 1. Introduction At the beginning of the 20th century, there were several works concerned with the dynamics of fluid penetration into 1.1. -

Capillary Action Experiment
Discover How Capillary Action Works with the Walking Water Experiment Grades: K - 6 Time: 20 mins set-up; view results the next day Lesson summary: Students will learn about capillary action. What’s the big idea? Outcomes or purpose: Water can move through tubes or Capillary action is when a liquid, like water, moves porous materials through a process up something solid, like a tube or into a material called capillary action. with a lot of small holes. Capillary action works against gravity because of three special forces called cohesion, adhesion and surface tension. Teacher background: Capillary action is at work in LGT gardens every day. Can you name three examples? If you said: Growboxes, peat pellets and GrowEase capillary mat trays then you’re right! You get bonus points if you said plants too! So what is capillary action anyway? Capillary action is when a liquid, like water, moves up something solid, like a tube or into a material with a lot of small holes. Capillary action works against gravity because of three special forces called cohesion, adhesion and surface tension. Tiny particles of water - also called water molecules - are like a group of good friends. They like to stick together! So when one molecule meets other molecules they tend to stick together in a group. This is called cohesion. Water molecules also like to stick to solid things. Sticking to solid things is called adhesion. Some examples of solids are: paper towels, the sides of a hollow tube or growing medium. All of these things have one thing in common: they are porous. -
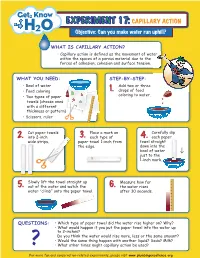
EXPERIMENT 17: CAPILLARY ACTION Objective: Can You Make Water Run Uphill?
EXPERIMENT 17: CAPILLARY ACTION Objective: Can you make water run uphill? WHAT IS CAPILLARY ACTION? • Capillary action is defined as the movement of water within the spaces of a porous material due to the forces of adhesion, cohesion and surface tension. WHAT YOU NEED: STEP-BY-STEP: • Bowl of water 1. Add two or three • Food coloring drops of food • Two types of paper coloring to water. towels (choose ones with a different thickness or pattern) • Scissors, ruler 2. Cut paper towels 3. Place a mark on 4. Carefully dip into 2-inch each type of each paper wide strips. paper towel 1-inch from towel straight the edge. down into the bowl of water just to the 1-inch mark. 5. Slowly lift the towel straight up 6. Measure how far out of the water and watch the the water rises water “climb” onto the paper towel. after 30 seconds. QUESTIONS: • Which type of paper towel did the water rise higher on? Why? • What would happen if you put the paper towel into the water up to 2-inches? Do you think the water would rise more, less or the same amount? ? • Would the same thing happen with another liquid? Soda? Milk? • What other times might capillary action be used? For more fun and conservation-related experiments, please visit www.plumbingexcellence.org EXPERIMENT 17: CAPILLARY ACTION Instructor’s Guide ALIGNMENT WITH ILLINOIS STATE BOARD OF EDUCATION GOALS State Goal 11: State Goal 12: State Goal 13: Section A: 2a, 2b, 2c, Section D: 2b Section A: 2b and 2c 2d, 2e and 2f WHAT’S HAPPENING? Everyone knows that moving water tends to flow downhill and standing water will seek its own level, but sometimes water can run uphill. -

Understanding Moisture Penetration of the Drainage Plane: a Building Science Principle Use Font Size 40
Ralph E. Moon, Ph.D. CHMM, CIAQP, MRSA GHD, Inc. [email protected] 813-971-3882 (office) 813-257-0838 (desk) Understanding Moisture Penetration of the Drainage Plane: A Building Science Principle Use Font size 40 2019 IAQA Annual Meeting Why is this relevant to the IAQ professional? • The fundamental role of any structure is to keep water out • The drainage plane constitutes the elements that protect the structure and prevent water penetration • Understanding how water penetrates a structure is necessary to identify why indoor air quality may be impaired 2019 IAQA Annual Meeting The Four Basic Rules of Water Damage • Porous materials “suck” via capillary action • Water vapor diffuses from a higher to a lower concentration gradient • Air carrying water vapor moves from high pressure to low pressure • Water runs downhill by gravity 2019 IAQA Annual Meeting Basic Rule of Water Damage No. 4 • Water runs downhill by gravity (i.e., roof and flashing leaks, attic condensation) 2019 IAQA Annual Meeting Five Forces of Rainwater Penetration • Gravity • Surface Tension • Capillary Action • Momentum (Kinetic Energy) • Air Pressure Differences 2019 IAQA Annual Meeting 2019 IAQA Annual Meeting Which forces of drainage are shown? 1. Drip 2. Stucco Cracks 3. Failed vent cover Edge Gravity Surface Tension QUIZ Capillary Action Question Momentum (Kinetic Energy) Air Pressure Differences 2019 IAQA Annual Meeting Four Strategies to Prevent Rainwater Penetration: 4 D’s • Deflection • Drainage • Drying • Durable Materials Stave Church at Urnes, Norway – Norway’s oldest stave church that dates back to the early 12th century in its present form. Wooden components of an even older church were used to build it. -

The Lost Chromatography Lesson
The Lost Chromatography Lesson Background Science Summary: The wonder of the chromatography experiment, whether on earth or in the zero-G heavens, is the capillary action of water movement in the filter paper strip. Defying both the force of gravity and the expected inertia of the water drop, the liquid advances toward the ink spot. Were it not for an understanding of capillary action, the gradual soaking toward the ink spot would be a mystery. Indeed, what is the process which separates various colors of ink from the ink spot? How it works: Though ink appears to be composed of one color, it is not. Actually, several colored pigments blend together to make the color. This is known as a mixture. Artists mix different paint colors, like red, blue and green, to achieve a desired color which is a combination of the three basic colors. Because of chromatography, ink becomes soaked in the water drop so that the different pigments begin to separate or “bleed” apart. This results in the true colors being discovered. For Christa, one of the true colors in the black ink spot separated out by chromatography was blue. But more discussion of the science is needed. Why does one ink separate apart from another, and why does the water move toward the ink spot in the filter paper strip? The first question’s answer is: When a substance dissolves in a liquid like water, it is said to be soluble. Since this quality of being soluble differs in substances, each color will dissolve at a different rate so ink color separation occurs as the water soaks into the black ink spot. -

Surface Tension, Viscosity, and Capillary Action Vaporization And
Chapter 11 Liquids, Solids, and Intermolecular Forces 435 11.60 (a) This will form a homogeneous solution. There will only be dispersion forces present. (b) This will not form a homogeneous solution, since one is polar and one is nonpolar. (c) This will form a homogeneous solution. There will be ion-dipole interactions between the Li+ and NO3~ ions and the water molecules. There will also be dispersion forces, dipole-dipole forces, and hydrogen bonding between the water molecules. (d) This will not form a homogeneous solution, since one is polar and one is nonpolar. Surface Tension, Viscosity, and Capillary Action 11.61 Water will have the higher surface tension since it exhibits hydrogen bonding, a strong intermolecular force. Acetone cannot form hydrogen bonds. 11.62 (a) Water "wets" surfaces that are capable of dipole-dipole interactions. The water will form strong adhesive forces with the surface when these dipole-dipole forces are present and so the water will spread to cover as much of the surface as possible. Water does not experience strong intermolecular forces with oil and other nonpolar surfaces. The water will bead up, maximizing the cohesive inter- actions, which involve strong hydrogen bonds. So water will bead up on surfaces that can only exhibit dispersion forces. (b) Mercury will bead up on surfaces since it is not capable of forming strong intermolecular interactions (only dispersion forces). 11.63 Compound A will have the higher viscosity since it can interact with other molecules along the entire mol- ecule. The more branched isomer has a smaller surface area allowing for fewer interactions.