Sand, Semivariogram, Ordinary Kriging
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

PBAPP Seeks Another Cloud Seeding Move to Fill Penang Dams
PBAPP seeks another cloud seeding move to fill Penang dams (File pic) The Penang Water Supply Corporation (PBAPP) is seeking for a second series of six additional cloud seeding operations next month to replenish two dams. -NSTP/MIKAIL ONG By Audrey Dermawan - May 28, 2020 @ 6:36pm GEORGE TOWN: The Penang Water Supply Corporation (PBAPP) is seeking for a second series of six additional cloud seeding operations next month to replenish two dams that were still below the 50 per cent capacity mark. The two dams are the Air Itam Dam and Teluk Bahang Dam. Cloud seeding operations conducted between April 25 and yesterday have helped to increase the effective capacities of both dams, but these were still not enough to boost the water levels. The maximum effective capacity of the Air Itam Dam is 2.16 billion litres, while the maximum effective capacity of the Teluk Bahang Dam is 18.24 billion litres. The effective capacity of the Teluk Bahang Dam is 8.4 times more than the effective capacity of the Air Itam Dam. PBAPP chief executive officer Datuk Jaseni Maidinsa said while there had been improvements following the earlier cloud seeding operations, the effective capacities of both dams were still below normal levels. https://www.nst.com.my/news/nation/2020/05/596030/pbapp-seeks-another-cloud-seeding-move-fill-penang-dams "In March, the Penang government approved a first series of 10 cloud seeding operations over Penang and Kedah. To date, six cloud seeding operations have been carried out with four more to go. "PBAPP is requesting for a second series of six additional cloud seeding operations in June to maximise potential rainfall yield and refill the Air Itam Dam and Teluk Bahang Dam as much as possible," he said today. -

Pa International Property Consultants
PA INTERNATIONAL PROPERTY CONSULTANTS (PENANG) SDN BHD REAL ESTATE (PENANG) SDN BHD PA international Property Consultants Sdn Bhd formed in June 1980, is a full service real estate company registered with the board of valuers, appraisers & estate agents under the valuers, appraisers and estate agents act 1981. Our Network Offices: Our Professional Services: 1. Johor Bahru, Johor 1. Property Valuation 2. Kluang, Johor 2. Compulsory Land 3. Kuala Lumpur/ Petaling Acquisition and Jaya Compensation 4. Klang, Selangor 3. Property Selling & Leasing 5. Penang 4. Property Investment 6. Ipoh, Perak Consultancy 7. Seremban, Negeri 5. Project Marketing Sembilan 6. Property Management 8. Sungai Petani, Kedah 7. Corporate & Advisory 9. Ho Chi Minh City, Vietnam 8. Property Market Research (Representative Office) & Consultancy PA INTERNATIONAL PROPERTY CONSULTANTS (PENANG) SDN BHD PA international Property Consultants (Penang) Sdn Bhd was established in year 2014, head by Sr. Michael Loo as Executive Director. The company have undertaken valuations and related assignments for a number of Public listed and other established corporate entities, among which are: Tambun Indah Land Berhad Tah Wah Group Sdn Bhd Hai Hong Development Sdn Bhd Ivory Properties Group Berhad VST Group Sdn Bhd United Oil Palm Industries Sdn Bhd LBI Capital Berhad Sunrise Manner Sdn Bhd Hwa Huat Livestock Industries Sdn Bhd Hua Yang Berhad Metro Jelata Sdn Bhd Jeenhuat Foodstuffs Industries Sdn Tatt Giap Group Berhad Sunway Properties Berhad Bhd Wing Tai Malaysia Berhad Asia Plywood Company SL Airmas Development Sdn Bhd Heng Huat Resources Group Berhad Berhad Chye Seng Sdn Bhd Boon Koon Group Berhad VST Group Sdn Bhd The Light Hotel (M) Sdn Bhd B. -

Penang: Where to Stay to Make the Most of Your Holiday
Select Page a Penang: Where to Stay to Make the Most of Your Holiday When you are planning your trip to Penang, where to stay is the most crucial feature that can make or break your holiday. There are so many hotels in Penang, Malaysia. And a lot of blogs list them off like Trip Advisor. But the ones I’ve picked for you below are special. Most of these hotels, especially the ones in Georgetown, are unique to Penang. You can always find a cheap hotel in Penang. Some hostels are only RM20 a night. I haven’t chosen by cheap, I’ve chosen by awesome! Some are affordable, some are expensive, choose your poison. It’s almost impossible to choose the best hotel in Penang. So I’ve chosen my faves… all 17 of them, across six neighborhoods. Each neighborhood I review is vastly different and not for everyone. I hope it helps because this blog was a whopper to write. If you’re not sure where to stay in Penang, you are in the right place. I’m an insider who knows this island like the back of my hand. Grab a glass of wine, settle in, and take notes. I’ve got you covered. Let’s dig in. But first… a map. Penang: Where to Stay Map data ©2020 Google Terms 5 km Contents: 1. Georgetown or George Town? It depends 1.1. Georgetown is for you if you are a: 1.2. Georgetown is NOT for you if you are a: 1.3. What to see and do in Georgetown: 2. -

Penang Travel Tale
Penang Travel Tale The northern gateway to Malaysia, Penang’s the oldest British settlement in the country. Also known as Pulau Pinang, the state capital, Georgetown, is a UNESCO listed World Heritage Site with a collection of over 12,000 surviving pre-war shop houses. Its best known as a giant beach resort with soft, sandy beaches and plenty of upscale hotels but locals will tell you that the island is the country’s unofficial food capital. SIM CARDS AND DIALING PREFIXES Malaysia’s three main cell phone service providers are Celcom, Digi and WEATHER Maxis. You can obtain prepaid SIM cards almost anywhere – especially Penang enjoys a warm equatorial climate. Average temperatures range inside large-scale shopping malls. Digi and Maxis are the most popular between 29°C - 35 during the day and 26°C - 29°C during the night; services, although Celcom has the most widespread coverage in Sabah however, being an island, temperatures here are often higher than the and Sarawak. Each state has its own area code; to make a call to a mainland and sometimes reaches as high as 35°C during the day. It’s best landline in Penang, dial 04 followed by the seven-digit number. Calls to not to forget your sun block – the higher the SPF, the better. It’s mostly mobile phones require a three-digit prefix, (Digi = 016, Maxis = 012 and sunny throughout the day except during the monsoon seasons when the Celcom = 019) followed by the seven digit subscriber number. island experiences rainfall in the evenings. http://www.penang.ws /penang-info/clim ate.htm CURRENCY GETTING AROUND Malaysia coinage is known as the Ringgit Malaysia (MYR). -

PCEB Destination Brochure.Pdf
CONTENT PENANG FACTOR 2 LAND OF HERITAGE 4 FACTS ABOUT PENANG 6 GLOBAL CONNECTIVITY 8 EXPERIENCES UNFILTERED 10 RADIANT CULTURE 12 MELODIOUS HARMONY 14 PRIZED HERITAGE 16 VIBRANT FESTIVALS 18 LUSTROUS NATURE 20 VENUES ABOUND 22 COLONIAL SPLENDOUR 24 GARDEN EXTRAVAGANZA 26 HERITAGE CHARM 28 RESORT LUXURY 30 CONVENTION CONVERGENCE 32 URBAN ELEGANCE 34 ABOUT PCEB 36 Cheong Fatt Tze Mansion © Sherwynd Rylan Kessler 1 PENANG FACTOR The Northern Malaysian state of Penang is a magical place steeped in rich history and heritage set amidst the backdrop of a thriving and modern city. The captivating fusion of old and new has cultivated one of Southeast Asia’s most vibrant cities and one of the world’s must visit places. With its bold gastronomical culture, charming colonial architecture, and beautiful nature hotspots, Penang offers the best of Asia to the world. Penang’s incomparable architecture, inspiring cuisine, colourful culture and sincere hospitality offers visitors an authentic and exceptional Asian experience. Wisma Yeap Chor Ee © Norlman Lo 3 LAND OF HERITAGE NIO M O UN IM D R T IA A L • P • W L O A I R D L D N H O E M R I E TA IN G O E • PATRIM George Town is a living testimony of the multi-cultural heritage and traditions of Asia, where diverse cultures and religion met and have coexisted in harmony for generations. In 2008, George Town was recognised for its outstanding universal value by UNESCO’s World Heritage Convention. The heritage enclave, according to UNESCO, represents a remarkable example of the historic colonial towns on the Straits of Malacca. -

(Emeer 2008) State: Pulau Pinang
LIST OF INSTALLATIONS AFFECTED UNDER EFFICIENT MANAGEMENT OF ELECTRICAL ENERGY REGULATIONS 2008 (EMEER 2008) STATE: PULAU PINANG No. Installation Name Address BADAN PENGURUSAN BERSAMA PRANGIN MALL, PEJABAT 1 PRANGIN MALL PENGURUSAN, TINGKAT 5, PRANGIN MALL, NO.33, JALAN DR. LIM CHWEE LEONG, 10100 PULAU PINANG 161,KAWASAN INDUSTRI,11900 BAYAN LEPAS FTZ,BAYAN LEPAS, PULAU 2 RAPID PRECISION PINANG 3 TECO INDUSTRY (MALAYSIA) 535/539,LRG PERUSAHAAN BARU,13600 PERAI,PULAU PINANG 4 MEGAMALL PENANG 2828, JALAN BARU, BANDAR PERAI JAYA, 13600 PERAI, PULAU PINANG PLOT 17A,JLN PERUSAHAAN,13600 KAWASAN PERINDUSTRIAN PRAI 5 METECH ALUMINIUM SDN BHD IV,PRAI, PULAU PINANG ALLIANCE RUBBER PRODUCTS SDN 2714, LRG INDUSTRI 15, KAWASAN PERINDUSTRIAN BKT PANCHOR, 6 BHD NIBONG TEBAL, 14300, PULAU PINANG BENCHMARK ELECTRONICS (M) SDN PLOT 17A & B, TECHNOPLEX, MEDAN BAYAN LEPAS, BAYAN LEPAS 7 BHD - PRECISION TECHNOLOGIES INDUSTRIAL PARK, PHASE 4, 11900 BAYAN LEPAS, PULAU PINANG NO. 2515, TINGKAT PERUSAHAAN 4A, PERAI FREE TRADE ZONE, 13600 8 TONG HEER FASTENERS CO. SDN BHD PERAI, PULAU PINANG 9 NI MALAYSIA SDN BHD NO. 8, LEBUH BATU MAUNG 1, 11960 BAYAN LEPAS, PULAU PINANG 10 EPPOR-PACK SDN BHD 2263, PERMATANG KLING, 14300 NIBONG TEBAL, PULAU PINANG FLEXTRONICS SYSTEMS (PENANG) PMT 719, LINGKARAN CASSIA SELATAN, 14100 SIMPANG AMPAT, PULAU 11 SDN BHD PINANG 12 GURNEY PARAGON MALL 163-D, PERSIARAN GURNEY, 10250, PULAU PINANG BENCHMARK ELECTRONICS (M) SDN BAYAN LEPAS FREE INDUSTRIAL ZONE PHASE 1, 11900 BAYAN LEPAS, 13 BHD - ELECTRONIC MANUFACTURING PULAU PINANG SERVICES -
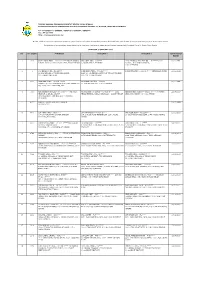
Fax : 04-2613453 Http : // BIL NO
TABUNG AMANAH PINJAMAN PENUNTUT NEGERI PULAU PINANG PEJABAT SETIAUSAHA KERAJAAN NEGERI PULAU PINANG TINGKAT 25, KOMTAR, 10503 PULAU PINANG Tel : 04-6505541 / 6505599 / 6505165 / 6505391 / 6505627 Fax : 04-2613453 Http : //www.penang.gov.my Berikut adalah senarai nama peminjam-peminjam yang telah menyelesaikan keseluruhan pinjaman dan tidak lagi terikat dengan perjanjian pinjaman penuntut Negeri Pulau Pinang Pentadbiran ini mengucapkan terima kasih di atas komitmen tuan/puan di dalam menyelesaikan bayaran balik Pinjaman Penuntut Negeri Pulau Pinang SEHINGGA 31 JANUARI 2020 BIL NO AKAUN PEMINJAM PENJAMIN 1 PENJAMIN 2 TAHUN TAMAT BAYAR 1 371 QUAH LEONG HOOI – 62121707**** NO.14 LORONG ONG LOKE JOOI – 183**** TENG EE OO @ TENG EWE OO – 095**** 4, 6TH 12/07/1995 SUNGAI BATU 3, 11920 BAYAN LEPAS, PULAU PINANG. 6, SOLOK JONES, P PINANG AVENUE, RESERVOIR GARDEN , 11500 P PINANG 2 8 LAU PENG KHUEN – 51062707 KHOR BOON TEIK – 47081207**** CHOW PENG POY – 09110207**** MENINGGAL DUNIA 31/12/1995 62 LRG NANGKA 3, TAMAN DESA DAMAI, BLOK 100-2A MEWAH COURT, JLN TAN SRI TEH EWE 14000 BUKIT MERTAJAM LIM, 11600 PULAU PINANG 3 1111 SOO POOI HUNG – 66121407**** IVY KHOO GUAT KIM – 56**** - 22/07/1996 BLOCK 1 # 1-7-2, PUNCAK NUSA KELANA CONDO JLN 10 TMN GREENVIEW 1, 11600 P PINANG PJU 1A/48, 47200 PETALING JAYA 4 343 ROHANI BINTI KHALIB – 64010307**** NO 9 JLN MAHMUD BIN HJ. AHMAD – 41071305**** 1962, NOORDIN BIN HASHIM – 45120107**** 64 TAMAN 22/07/1997 JEJARUM 2, SEC BS 2 BUKIT TERAS JERNANG, BANGI, SELANGOR. - SUDAH PINDAH DESA JAYA, KEDAH, 08000 SG.PETANI SENTOSA, BUKIT SENTOSA, 48300 RAWANG, SELANGOR 5 8231 KHAIRIL TAHRIRI BIN ABDUL KHALIM – - - 16/03/1999 80022907**** 6 7700 LIM YONG HOOI – A345**** LIM YONG PENG – 74081402**** GOH KIEN SENG – 73112507**** 11/11/1999 104 18-A JALAN TAN SRI TEH, EWE LIM, 104 18-A JLN T.SRI TEH EWE LIM, 11600 PULAU 18-I JLN MUNSHI ABDULLAH, 10460 PULAU PINANG 11600 PULAU PINANG PINANG 7 6605 CHEAH KHING FOOK – 73061107**** NO. -

Penang Travel Guide
PENANG TRAVEL GUIDE ___________________________________________________________________________________________________________________________________________________ 4D3N ITINERARY By 1Step1Footprint.com Penang 4D3N Itinerary DAY 1 1300 hrs Check in to 24 Merican Road Airbnb 1430 hrs Lunch at Siam Road Yan Yam Café, Georgetown Recommend: Penang Fried Laksa 1530 hrs Penang Road Famous Teo Chew Chendul 1630 hrs Batu Ferringhi Beach Take Bus 101 from KOMTAR Interchange to Batu Ferringhi 1900 hrs Dinner at Kimberley Street, Georgetown Recommend: Duck Kuey Chap at Restoran Kimberly & various desserts (四果汤) 2100 hrs Return to Airbnb and rest DAY 2 0700 hrs Depart for Penang Hill (Bukit Bendera) Take Bus 204 from the bus stop across Jln. Dato’ Keramat and alight at Penang Hill Terminal 1130 hrs Lunch at Pasar Air Itam Recommend: The famous Air Itam Laksa 1300 hrs Kek Lok Si Temple 1730 hrs Dinner at Siam Road Charcoal Char Kuey Teow, Georgetown 1930 hrs Shopping at Prangin Mall 2100 hrs Supper at New Lane Night Hawker Recommend: Eng Kee Fried Oyster Omelette Penang 4D3N Itinerary DAY 3 0900 hrs Breakfast at Timesway or Kuantan Road Hawker 1100 hrs Visit the Sleeping Buddha of Wat Chayamangkalaram Temple at Burma Road. 1230 hrs Lunch at Lebuh Campbell’s Hong Kee Wan Thun Mee, Georgetown 1400 hrs Visit Georgetown’s heritage buildings such as Khoo Kongsi & Cheah Kongsi Mansions 1500 hrs Visit the Pinang Peranakan Mansion (Filming location of popular Singapore drama series “Little Nyonya” 1600 hrs Street art hunting at Lebuh Armenian where the most famous “Little Children on a Bicycle” street art is located 1730 hrs Clan Jetties – local neighbourhood on stilts over the sea 1900 hrs Dinner at China House 2030 hrs Supper at New Lane or return to Airbnb and rest DAY 4 0930 hrs Breakfast at Ah Leng Char Kuey Tow Recommend: The Special with fried duck egg 1200 hrs Check out from 24 Merican Road - End of Trip - PENANG FOOD A trip to Penang will not be fruitful without savouring its local delicacies. -

The State of Penang, Malaysia
Please cite this paper as: National Higher Education Research Institute (2010), “The State of Penang, Malaysia: Self-Evaluation Report”, OECD Reviews of Higher Education in Regional and City Development, IMHE, http://www.oecd.org/edu/imhe/regionaldevelopment OECD Reviews of Higher Education in Regional and City Development The State of Penang, Malaysia SELF-EVALUATION REPORT Morshidi SIRAT, Clarene TAN and Thanam SUBRAMANIAM (eds.) Directorate for Education Programme on Institutional Management in Higher Education (IMHE) This report was prepared by the National Higher Education Research Institute (IPPTN), Penang, Malaysia in collaboration with a number of institutions in the State of Penang as an input to the OECD Review of Higher Education in Regional and City Development. It was prepared in response to guidelines provided by the OECD to all participating regions. The guidelines encouraged constructive and critical evaluation of the policies, practices and strategies in HEIs’ regional engagement. The opinions expressed are not necessarily those of the National Higher Education Research Institute, the OECD or its Member countries. Penang, Malaysia Self-Evaluation Report Reviews of Higher Education Institutions in Regional and City Development Date: 16 June 2010 Editors Morshidi Sirat, Clarene Tan & Thanam Subramaniam PREPARED BY Universiti Sains Malaysia, Penang Regional Coordinator Morshidi Sirat Ph.D., National Higher Education Research Institute, Universiti Sains Malaysia Working Group Members Ahmad Imran Kamis, Research Centre and -
Chapter 4: Environment
Penang Economic and Development Report 153 2019/2020 4. Environment Environmental quality is considered to be a public levels of up to 50 are considered good, between 51 good. It affects the public and the community in and 100 moderate, 101 and 200 unhealthy, 201 and terms of economic, social welfare, and quality of 300 very unhealthy, and 300 and above hazardous. life. Ecological sustainability is a key factor for An API system includes the major air pollutants sustainable economic and social development. which may cause potential harm to human health if The most pressing environmental issues in Penang they reach unsafe levels. The air pollutants included are air and water pollution, flash floods, waste in Malaysia’s API are ozone (O3), carbon monoxide management, and landslides. Short-term action is (CO), nitrogen dioxide (NO2), sulphur dioxide (SO2), needed while maintaining a long-term perspective. suspended particulate matter of less than 10 microns in size (PM10) and suspended particulate matter of less than 2.5 microns in size (PM2.5) (Department of 4.1 Pollution Environment Malaysia, 2018). Different types of environmental pollution have The air quality of Penang is monitored at four been reported in Penang, the major ones being open stations, Seberang Jaya, Seberang Perai, Balik burning, air pollution, and water pollution. These Pulau, and Minden. In 2019, the overall air quality in pose serious risks to the environment, public health, Penang worsened as the number of days with good and even the economy. API levels decreased and the number of unhealthy days increased compared with 2018 (Table 4.1). -

Pulau Pinang 6,776.2 Foreign Direct Investment Foreign Directinvestment 3
4. Be aware of 1. Practise 3. Wash hands regularly Covid-19 physical distancing 2. Wear face masks with soap and sanitiser pandemic AUGUST 16 – 31, 2020 Super start to 2020 State records almost RM6.8 billion in approved manufacturing Remaining 4% (RM321.1m) is approved manufacturing FDI for the period of January to March this year. domestic direct investments (DDI). Top manufacturing FDI from Switzerland, the Last year Penang top in terms of approved United States and Singapore. manufacturing FDI with RM15 billion. State’s approved manufacturing FDI accounts for 96% of State attracts 32 manufacturing projects which are Penang’s manufacturing investment inflows in 1Q2020. expected to create 4,035 new job opportunities. * See P2 for full story Kedah Sarawak 651.7 822.9 Selangor Johor 984.3 Pulau Pinang 1,068.0 PENANG again 6,776.2 We are thankful for Foreign Direct Investment the strong confidence tops list of approved (RM million) manufacturing placed in us by the multinational corporations foreign direct – Chief Minister investments for 1Q2020 Chow Kon Yeow 2 NEWS AUGUST 16 – 31, 2020 BULETIN MUTIARA Story by Christopher Tan Pix by Law Suun Ting ESPITE the dark clouds of Covid-19 hanging over Penang tops Dthe whole world, Penang has something to cheer about. The state has again topped the list of approved manufactur- ing foreign direct investments (FDI) for the first quarter of this FDI chart year (1Q2020) - after taking pole position with RM15 billion for manufacturing FDI for the first Penang expects 2020’s invest- the whole of last year. quarter of this year were from ment inflow to the state to be For the period of January to Switzerland, the United States lower than the 2019 all-time- March this year, Penang record- and Singapore. -

SENARAI PREMIS PENGINAPAN PELANCONG : P.PINANG 1 Berjaya Penang Hotel 1-Stop Midlands Park,Burmah Road,Timur Laut 10350 Timur La
SENARAI PREMIS PENGINAPAN PELANCONG : P.PINANG BIL. NAMA PREMIS ALAMAT POSKOD DAERAH 1 Berjaya Penang Hotel 1-Stop Midlands Park,Burmah Road,Timur Laut 10350 Timur Laut 2 The Bayview Beach Resort 25-B,Lebuh Farquha, Timur Laut 10200 Timur Laut 3 Evergreen Laurel Hotel 53, Persiaran Gurney 10250 Georgetown 4 CITITEL PENANG 66,Jln Penang 10000 Georgetown 5 Oriental Hotel 105, Jln Penang 10000 Georgetown 6 Sunway Hotel Georgetown 33, Lorong Baru, Off Jln Macalister 10400 Georgetown 7 Sunway Hotel Seberang Jaya No.11, Lebuh Tenggiri 2, Pusat Bandar Seberang Jaya 13700 Seberang Jaya 8 Hotel Neo + Penang No.68 Jalan Gudwara, Town Pulau Pinang 10300 Georgetown 9 Golden Sand Resort Penang By Shangri-La 10th Mile, Batu Ferringhi, Timur Laut 11100 Batu Ferringhi 10 Bayview Hotel Georgetown Penang 25-A, Farquhar Street 10200 Georgetown 11 Park Royal Penang Resort Batu Ferringhi 11100 Batu Ferringhi 12 Hotel Sri Malaysia Penang No.7,Jln Mayang Pasir 2 11950 Bandar Bayan Baru 13 Rainbow Paradise Beach Resort 527,Jln Tanjung Bungah 11200 Tanjung Bungah 14 Equatorial Hotel Penang No.1,Jln Bukit Jambul 11900 Bayan Lepas 15 Shangri-La's Rasa Sayang Resort & Spa Batu Ferringhi Beach 11100 Batu Ferringhi 16 Hotel Continental No.5, Jln Penang 10000 Georgetown 17 Hotel Noble 36,Lorong Pasar 10200 Georgetown 18 Pearl View Hotel 2933, Jln Baru 13600 Butterworth 19 Eastern and Oriental Hotel 10, Leboh Farquhar 10200 Georgetown 20 Modern Hotel 179-C, Labuh Muntri 10200 Georgetown 21 Garden Inn 41, Anson Road 10400 Georgetown 22 Pin Seng Hotel 82, Lorong Cinta 10200 Georgetown 23 Hotel Eng Loh 48, Church Street 10200 Georgetown 24 Hotel Apollo 4475, Jln Kg.