Working Group Report: a Brief History of Trigonometry for Mathematics Educators
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

A Genetic Context for Understanding the Trigonometric Functions Danny Otero Xavier University, [email protected]
Ursinus College Digital Commons @ Ursinus College Transforming Instruction in Undergraduate Pre-calculus and Trigonometry Mathematics via Primary Historical Sources (TRIUMPHS) Spring 3-2017 A Genetic Context for Understanding the Trigonometric Functions Danny Otero Xavier University, [email protected] Follow this and additional works at: https://digitalcommons.ursinus.edu/triumphs_precalc Part of the Curriculum and Instruction Commons, Educational Methods Commons, Higher Education Commons, and the Science and Mathematics Education Commons Click here to let us know how access to this document benefits oy u. Recommended Citation Otero, Danny, "A Genetic Context for Understanding the Trigonometric Functions" (2017). Pre-calculus and Trigonometry. 1. https://digitalcommons.ursinus.edu/triumphs_precalc/1 This Course Materials is brought to you for free and open access by the Transforming Instruction in Undergraduate Mathematics via Primary Historical Sources (TRIUMPHS) at Digital Commons @ Ursinus College. It has been accepted for inclusion in Pre-calculus and Trigonometry by an authorized administrator of Digital Commons @ Ursinus College. For more information, please contact [email protected]. A Genetic Context for Understanding the Trigonometric Functions Daniel E. Otero∗ July 22, 2019 Trigonometry is concerned with the measurements of angles about a central point (or of arcs of circles centered at that point) and quantities, geometrical and otherwise, that depend on the sizes of such angles (or the lengths of the corresponding arcs). It is one of those subjects that has become a standard part of the toolbox of every scientist and applied mathematician. It is the goal of this project to impart to students some of the story of where and how its central ideas first emerged, in an attempt to provide context for a modern study of this mathematical theory. -

Refresher Course Content
Calculus I Refresher Course Content 4. Exponential and Logarithmic Functions Section 4.1: Exponential Functions Section 4.2: Logarithmic Functions Section 4.3: Properties of Logarithms Section 4.4: Exponential and Logarithmic Equations Section 4.5: Exponential Growth and Decay; Modeling Data 5. Trigonometric Functions Section 5.1: Angles and Radian Measure Section 5.2: Right Triangle Trigonometry Section 5.3: Trigonometric Functions of Any Angle Section 5.4: Trigonometric Functions of Real Numbers; Periodic Functions Section 5.5: Graphs of Sine and Cosine Functions Section 5.6: Graphs of Other Trigonometric Functions Section 5.7: Inverse Trigonometric Functions Section 5.8: Applications of Trigonometric Functions 6. Analytic Trigonometry Section 6.1: Verifying Trigonometric Identities Section 6.2: Sum and Difference Formulas Section 6.3: Double-Angle, Power-Reducing, and Half-Angle Formulas Section 6.4: Product-to-Sum and Sum-to-Product Formulas Section 6.5: Trigonometric Equations 7. Additional Topics in Trigonometry Section 7.1: The Law of Sines Section 7.2: The Law of Cosines Section 7.3: Polar Coordinates Section 7.4: Graphs of Polar Equations Section 7.5: Complex Numbers in Polar Form; DeMoivre’s Theorem Section 7.6: Vectors Section 7.7: The Dot Product 8. Systems of Equations and Inequalities (partially included) Section 8.1: Systems of Linear Equations in Two Variables Section 8.2: Systems of Linear Equations in Three Variables Section 8.3: Partial Fractions Section 8.4: Systems of Nonlinear Equations in Two Variables Section 8.5: Systems of Inequalities Section 8.6: Linear Programming 10. Conic Sections and Analytic Geometry (partially included) Section 10.1: The Ellipse Section 10.2: The Hyperbola Section 10.3: The Parabola Section 10.4: Rotation of Axes Section 10.5: Parametric Equations Section 10.6: Conic Sections in Polar Coordinates 11. -

International Journal for Scientific Research & Development| Vol. 5, Issue 12, 2018 | ISSN (Online): 2321-0613
IJSRD - International Journal for Scientific Research & Development| Vol. 5, Issue 12, 2018 | ISSN (online): 2321-0613 A Case Study on Applications of Trigonometry in Oceanography Suvitha M.1 Kalaivani M.2 1,2Student 1,2Department of Mathematics 1,2Sri Krishna Arts and Science College, Coimbatore, Tamil Nadu, India Abstract— This article introduces a trigonometric field that bisected to create two right-angle triangles, most problems extends in the field of real numbers adding two elements: sin can be reduced to calculations on right-angle triangles. Thus and cos satisfying an axiom sin²+cos²=1.It is shown that the majority of applications relate to right-angle triangles. assigning meaningful names to particular elements to the One exception to this is spherical trigonometry, the study of field, All know trigonometric identities may be introduced triangles on spheres, surfaces of constant positive curvature, and proved. The main objective of this study is about in elliptic geometry (a fundamental part of astronomy and oceanography how the oceanographers guide everyone with navigation). Trigonometry on surfaces of negative curvature the awareness of the Tsunami waves and protect the marine is part of hyperbolic geometry. animals hitting the ships and cliffs. Key words: Trigonometric Identities, Trigonometric Ratios, II. HISTORY OF TRIGONOMETRY Trigonometric Functions I. INTRODUCTION A. Trigonometry Fig. 2: Hipparchus, credited with compiling the first trigonometric, is known as "the father of trigonometry". A thick ring-like shell object found at the Indus Fig. 1: Valley Civilization site of Lothal, with four slits each in two All of the trigonometric functions of an angle θ can be margins served as a compass to measure angles on plane constructed geometrically in terms of a unit circle centered at surfaces or in the horizon in multiples of 40degrees,upto 360 O. -
Algebra/Geometry/Trigonometry App Samples
Algebra/Geometry/Trigonometry App Samples Holt McDougal Algebra 1 HMH Fuse: Algebra 1- HMH Fuse is the first core K-12 education solution developed exclusively for the iPad. The portability of a complete classroom course on an iPad enables students to learn in the classroom, on the bus, or at home—anytime, anywhere—with engaging content that provides an individually-tailored learning experience. Students and educators using HMH Fuse: will benefit from: •Instructional videos that teach or re-teach all key concepts •Math Motion is a step-by-step interactive demonstration that displays the process to solve complex equations •Homework Help provides at-home support for intricate problems by providing hints for each step in the solution •Vocabulary support throughout with links to a complete glossary that includes audio definitions •Tips, hints, and links that enable students to acquire the help they need to understand the lessons every step of the way •Quizzes that assess student’s skills before they begin a concept and at strategic points throughout the chapters. Instant, automatic grading of quizzes lets students know exactly how they have performed •Immediate assessment results sent to teachers so they can better differentiate instruction. Sample- Cost is Free, Complete App price- $59.99 Holt McDougal HMH Fuse: Geometry- Following our popular HMH Fuse: Algebra 1 app, HMH Fuse: Geometry is the newest offering in the HMH Fuse series. HMH Fuse: Geometry will allow you a sneak peek at the future of mobile geometry curriculum and includes a FREE sample chapter. HMH Fuse is the first core K-12 education solution developed exclusively for the iPad. -
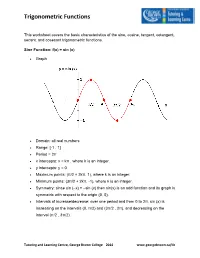
Trigonometric Functions
Trigonometric Functions This worksheet covers the basic characteristics of the sine, cosine, tangent, cotangent, secant, and cosecant trigonometric functions. Sine Function: f(x) = sin (x) • Graph • Domain: all real numbers • Range: [-1 , 1] • Period = 2π • x intercepts: x = kπ , where k is an integer. • y intercepts: y = 0 • Maximum points: (π/2 + 2kπ, 1), where k is an integer. • Minimum points: (3π/2 + 2kπ, -1), where k is an integer. • Symmetry: since sin (–x) = –sin (x) then sin(x) is an odd function and its graph is symmetric with respect to the origin (0, 0). • Intervals of increase/decrease: over one period and from 0 to 2π, sin (x) is increasing on the intervals (0, π/2) and (3π/2 , 2π), and decreasing on the interval (π/2 , 3π/2). Tutoring and Learning Centre, George Brown College 2014 www.georgebrown.ca/tlc Trigonometric Functions Cosine Function: f(x) = cos (x) • Graph • Domain: all real numbers • Range: [–1 , 1] • Period = 2π • x intercepts: x = π/2 + k π , where k is an integer. • y intercepts: y = 1 • Maximum points: (2 k π , 1) , where k is an integer. • Minimum points: (π + 2 k π , –1) , where k is an integer. • Symmetry: since cos(–x) = cos(x) then cos (x) is an even function and its graph is symmetric with respect to the y axis. • Intervals of increase/decrease: over one period and from 0 to 2π, cos (x) is decreasing on (0 , π) increasing on (π , 2π). Tutoring and Learning Centre, George Brown College 2014 www.georgebrown.ca/tlc Trigonometric Functions Tangent Function : f(x) = tan (x) • Graph • Domain: all real numbers except π/2 + k π, k is an integer. -

Lecture 5: Complex Logarithm and Trigonometric Functions
LECTURE 5: COMPLEX LOGARITHM AND TRIGONOMETRIC FUNCTIONS Let C∗ = C \{0}. Recall that exp : C → C∗ is surjective (onto), that is, given w ∈ C∗ with w = ρ(cos φ + i sin φ), ρ = |w|, φ = Arg w we have ez = w where z = ln ρ + iφ (ln stands for the real log) Since exponential is not injective (one one) it does not make sense to talk about the inverse of this function. However, we also know that exp : H → C∗ is bijective. So, what is the inverse of this function? Well, that is the logarithm. We start with a general definition Definition 1. For z ∈ C∗ we define log z = ln |z| + i argz. Here ln |z| stands for the real logarithm of |z|. Since argz = Argz + 2kπ, k ∈ Z it follows that log z is not well defined as a function (it is multivalued), which is something we find difficult to handle. It is time for another definition. Definition 2. For z ∈ C∗ the principal value of the logarithm is defined as Log z = ln |z| + i Argz. Thus the connection between the two definitions is Log z + 2kπ = log z for some k ∈ Z. Also note that Log : C∗ → H is well defined (now it is single valued). Remark: We have the following observations to make, (1) If z 6= 0 then eLog z = eln |z|+i Argz = z (What about Log (ez)?). (2) Suppose x is a positive real number then Log x = ln x + i Argx = ln x (for positive real numbers we do not get anything new). -

Elementary Functions: Towards Automatically Generated, Efficient
Elementary functions : towards automatically generated, efficient, and vectorizable implementations Hugues De Lassus Saint-Genies To cite this version: Hugues De Lassus Saint-Genies. Elementary functions : towards automatically generated, efficient, and vectorizable implementations. Other [cs.OH]. Université de Perpignan, 2018. English. NNT : 2018PERP0010. tel-01841424 HAL Id: tel-01841424 https://tel.archives-ouvertes.fr/tel-01841424 Submitted on 17 Jul 2018 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Délivré par l’Université de Perpignan Via Domitia Préparée au sein de l’école doctorale 305 – Énergie et Environnement Et de l’unité de recherche DALI – LIRMM – CNRS UMR 5506 Spécialité: Informatique Présentée par Hugues de Lassus Saint-Geniès [email protected] Elementary functions: towards automatically generated, efficient, and vectorizable implementations Version soumise aux rapporteurs. Jury composé de : M. Florent de Dinechin Pr. INSA Lyon Rapporteur Mme Fabienne Jézéquel MC, HDR UParis 2 Rapporteur M. Marc Daumas Pr. UPVD Examinateur M. Lionel Lacassagne Pr. UParis 6 Examinateur M. Daniel Menard Pr. INSA Rennes Examinateur M. Éric Petit Ph.D. Intel Examinateur M. David Defour MC, HDR UPVD Directeur M. Guillaume Revy MC UPVD Codirecteur À la mémoire de ma grand-mère Françoise Lapergue et de Jos Perrot, marin-pêcheur bigouden. -

Two Editions of Ibn Al-Haytham's Completion of the Conics
Historia Mathematica 29 (2002), 247–265 doi:10.1006/hmat.2002.2352 Two Editions of Ibn al-Haytham’s Completion of the Conics View metadata, citation and similar papers at core.ac.uk brought to you by CORE Jan P. Hogendijk provided by Elsevier - Publisher Connector Mathematics Department, University of Utrecht, P.O. Box 80.010, 3508 TA Utrecht, Netherlands E-mail: [email protected] The lost Book VIII of the Conics of Apollonius of Perga (ca. 200 B.C.) was reconstructed by the Islamic mathematician Ibn al-Haytham (ca. A.D. 965–1041) in his Completion of the Conics. The Arabic text of this reconstruction with English translation and commentary was published as J. P. Hogendijk, Ibn al-Haytham’s Completion of the Conics (New York: Springer-Verlag, 1985). In a new Arabic edition with French translation and commentary (R. Rashed, Les mathematiques´ infinitesimales´ du IXe au XIe siecle.´ Vol. 3., London: Al-Furqan Foundation, 2000), it was claimed that my edition is faulty. In this paper the similarities and differences between the two editions, translations, and commentaries are discussed, with due consideration for readers who do not know Arabic. The facts will speak for themselves. C 2002 Elsevier Science (USA) C 2002 Elsevier Science (USA) C 2002 Elsevier Science (USA) 247 0315-0860/02 $35.00 C 2002 Elsevier Science (USA) All rights reserved. 248 JAN P. HOGENDIJK HMAT 29 AMS subject classifications: 01A20, 01A30. Key Words: Ibn al-Haytham; conic sections; multiple editions; Rashed. 1. INTRODUCTION The Conics of Apollonius of Perga (ca. 200 B.C.) is one of the fundamental texts of ancient Greek geometry. -

History of Mathematics in Mathematics Education. Recent Developments Kathy Clark, Tinne Kjeldsen, Sebastian Schorcht, Constantinos Tzanakis, Xiaoqin Wang
History of mathematics in mathematics education. Recent developments Kathy Clark, Tinne Kjeldsen, Sebastian Schorcht, Constantinos Tzanakis, Xiaoqin Wang To cite this version: Kathy Clark, Tinne Kjeldsen, Sebastian Schorcht, Constantinos Tzanakis, Xiaoqin Wang. History of mathematics in mathematics education. Recent developments. History and Pedagogy of Mathematics, Jul 2016, Montpellier, France. hal-01349230 HAL Id: hal-01349230 https://hal.archives-ouvertes.fr/hal-01349230 Submitted on 27 Jul 2016 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. HISTORY OF MATHEMATICS IN MATHEMATICS EDUCATION Recent developments Kathleen CLARK, Tinne Hoff KJELDSEN, Sebastian SCHORCHT, Constantinos TZANAKIS, Xiaoqin WANG School of Teacher Education, Florida State University, Tallahassee, FL 32306-4459, USA [email protected] Department of Mathematical Sciences, University of Copenhagen, Denmark [email protected] Justus Liebig University Giessen, Germany [email protected] Department of Education, University of Crete, Rethymnon 74100, Greece [email protected] Department of Mathematics, East China Normal University, China [email protected] ABSTRACT This is a survey on the recent developments (since 2000) concerning research on the relations between History and Pedagogy of Mathematics (the HPM domain). Section 1 explains the rationale of the study and formulates the key issues. -

Asian Contributions to Mathematics
PORTLAND PUBLIC SCHOOLS GEOCULTURAL BASELINE ESSAY SERIES Asian Contributions to Mathematics By Ramesh Gangolli Ramesh Gangolli Dr. Ramesh Gangolli was born in India, and educated at the University of Bombay, Cambridge University and MIT. He held the Cambridge Society of India Scholarship while at Cambridge University, and was a College Scholar at Peterhouse. During 1966-68 he was a Sloan Foundation Fellow. In 1967, he was awarded the Paul Levy Prize by a Committee of the French Academy of Sciences. At present he is a Professor of Mathematics at the University of Washington, Seattle. He has been active in mathematical research as well as in mathematics education, and has held visiting positions at many universities in the U.S. and abroad. He has served professionally in several capacities: as Chair of the mathematics of the Committee on Education of the American Mathematical Society, and as a member of several committees of the U.S. National Academy of Sciences and the National Research Council. He is also a musician specializing in the Classical Music of India, and is an Adjunct Professor of Music in the School of Music at the University of Washington. Version: 1999-12-22 PPS Geocultural Baseline Essay Series AUTHOR: Gangolli SUBJECT: Math Contents 1. INTRODUCTION. 1 1.1 Purpose of this essay. 1 1.2 Scope. 2 1.3 Acknowledgments. 3 2. SOME VIEWS OF THE DEVELOPMENT OF MATHEMATICS. 5 3. THE PLACE OF MATHEMATICS IN ANCIENT CULTURES. 10 3.1 Agriculture, commerce, etc. 11 3.2 Ritual, worship, etc. 12 3.3 Intellectual curiosity and amusement. -

By the Persian Mathematician and Engineer Abubakr
1 2 The millennium old hydrogeology textbook “The Extraction of Hidden Waters” by the Persian 3 mathematician and engineer Abubakr Mohammad Karaji (c. 953 – c. 1029) 4 5 Behzad Ataie-Ashtiania,b, Craig T. Simmonsa 6 7 a National Centre for Groundwater Research and Training and College of Science & Engineering, 8 Flinders University, Adelaide, South Australia, Australia 9 b Department of Civil Engineering, Sharif University of Technology, Tehran, Iran, 10 [email protected] (B. Ataie-Ashtiani) 11 [email protected] (C. T. Simmons) 12 13 14 15 Hydrology and Earth System Sciences (HESS) 16 Special issue ‘History of Hydrology’ 17 18 Guest Editors: Okke Batelaan, Keith Beven, Chantal Gascuel-Odoux, Laurent Pfister, and Roberto Ranzi 19 20 1 21 22 Abstract 23 We revisit and shed light on the millennium old hydrogeology textbook “The Extraction of Hidden Waters” by the 24 Persian mathematician and engineer Karaji. Despite the nature of the understanding and conceptualization of the 25 world by the people of that time, ground-breaking ideas and descriptions of hydrological and hydrogeological 26 perceptions such as components of hydrological cycle, groundwater quality and even driving factors for 27 groundwater flow were presented in the book. Although some of these ideas may have been presented elsewhere, 28 to the best of our knowledge, this is the first time that a whole book was focused on different aspects of hydrology 29 and hydrogeology. More importantly, we are impressed that the book is composed in a way that covered all aspects 30 that are related to an engineering project including technical and construction issues, guidelines for maintenance, 31 and final delivery of the project when the development and construction was over. -

Generating Highly Accurate Values for All Trigonometric Functions
GENERATING HIGHLY ACCURATE VALUES FOR ALL TRIGONOMETRIC FUNCTIONS INTRODUCTION: Although hand calculators and electronic computers have pretty much eliminated the need for trigonometric tables starting about sixty years ago, this was not the case back during WWII when highly accurate trigonometric tables were vital for the calculation of projectile trajectories. At that time a good deal of the war effort in mathematics was devoted to building ever more accurate trig tables some ranging up to twenty digit numerical accuracy. Today such efforts can be considered to have been a waste of time, although they were not so at the time. It is our purpose in this note to demonstrate a new approach for quickly obtaining values for all trigonometric functions exceeding anything your hand calculator can achieve. BASIC TRIGNOMETRIC FUNCTIONS: We begin by defining all six basic trigonometric functions by looking at the following right triangle- The sides a,b, and c of this triangle satisfy the Pythagorean Theorem- a2+b2=c2 we define the six trig functions in terms of this triangle as- sin()=b/c cos( )=a/c tan()=b/a csc()=c/b sec()=c/a) cot()=b/a From Pythagorous we also have at once that – 1 sin( )2 cos( )2 1 and [1 tan( )2 ] . cos( )2 It was the ancient Egyptian pyramid builders who first realized that the most important of these trigonometric functions is tan(). Their measure of this tangent was given in terms of sekels, where 1 sekhel=7. Converting each of the above trig functions into functions of tan() yields- tan( ) 1 sin( ) cos( ) tan( ) tan( ) 1 tan( )2 1 tan( )2 1 tan( )2 1 csc( ) sec( ) 1 tan( )2 cot( ) tan( ) tan( ) In using these equivalent definitions one must be careful of signs and infinities appearing in the approximations to tan().