Elements of Vector Calculus : Divergence and Curl of a Vector Field Lecture 3: Electromagnetic Theory Professor D
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Vector Calculus and Multiple Integrals Rob Fender, HT 2018
Vector Calculus and Multiple Integrals Rob Fender, HT 2018 COURSE SYNOPSIS, RECOMMENDED BOOKS Course syllabus (on which exams are based): Double integrals and their evaluation by repeated integration in Cartesian, plane polar and other specified coordinate systems. Jacobians. Line, surface and volume integrals, evaluation by change of variables (Cartesian, plane polar, spherical polar coordinates and cylindrical coordinates only unless the transformation to be used is specified). Integrals around closed curves and exact differentials. Scalar and vector fields. The operations of grad, div and curl and understanding and use of identities involving these. The statements of the theorems of Gauss and Stokes with simple applications. Conservative fields. Recommended Books: Mathematical Methods for Physics and Engineering (Riley, Hobson and Bence) This book is lazily referred to as “Riley” throughout these notes (sorry, Drs H and B) You will all have this book, and it covers all of the maths of this course. However it is rather terse at times and you will benefit from looking at one or both of these: Introduction to Electrodynamics (Griffiths) You will buy this next year if you haven’t already, and the chapter on vector calculus is very clear Div grad curl and all that (Schey) A nice discussion of the subject, although topics are ordered differently to most courses NB: the latest version of this book uses the opposite convention to polar coordinates to this course (and indeed most of physics), but older versions can often be found in libraries 1 Week One A review of vectors, rotation of coordinate systems, vector vs scalar fields, integrals in more than one variable, first steps in vector differentiation, the Frenet-Serret coordinate system Lecture 1 Vectors A vector has direction and magnitude and is written in these notes in bold e.g. -

A Brief Tour of Vector Calculus
A BRIEF TOUR OF VECTOR CALCULUS A. HAVENS Contents 0 Prelude ii 1 Directional Derivatives, the Gradient and the Del Operator 1 1.1 Conceptual Review: Directional Derivatives and the Gradient........... 1 1.2 The Gradient as a Vector Field............................ 5 1.3 The Gradient Flow and Critical Points ....................... 10 1.4 The Del Operator and the Gradient in Other Coordinates*............ 17 1.5 Problems........................................ 21 2 Vector Fields in Low Dimensions 26 2 3 2.1 General Vector Fields in Domains of R and R . 26 2.2 Flows and Integral Curves .............................. 31 2.3 Conservative Vector Fields and Potentials...................... 32 2.4 Vector Fields from Frames*.............................. 37 2.5 Divergence, Curl, Jacobians, and the Laplacian................... 41 2.6 Parametrized Surfaces and Coordinate Vector Fields*............... 48 2.7 Tangent Vectors, Normal Vectors, and Orientations*................ 52 2.8 Problems........................................ 58 3 Line Integrals 66 3.1 Defining Scalar Line Integrals............................. 66 3.2 Line Integrals in Vector Fields ............................ 75 3.3 Work in a Force Field................................. 78 3.4 The Fundamental Theorem of Line Integrals .................... 79 3.5 Motion in Conservative Force Fields Conserves Energy .............. 81 3.6 Path Independence and Corollaries of the Fundamental Theorem......... 82 3.7 Green's Theorem.................................... 84 3.8 Problems........................................ 89 4 Surface Integrals, Flux, and Fundamental Theorems 93 4.1 Surface Integrals of Scalar Fields........................... 93 4.2 Flux........................................... 96 4.3 The Gradient, Divergence, and Curl Operators Via Limits* . 103 4.4 The Stokes-Kelvin Theorem..............................108 4.5 The Divergence Theorem ...............................112 4.6 Problems........................................114 List of Figures 117 i 11/14/19 Multivariate Calculus: Vector Calculus Havens 0. -

Multivariable and Vector Calculus
Multivariable and Vector Calculus Lecture Notes for MATH 0200 (Spring 2015) Frederick Tsz-Ho Fong Department of Mathematics Brown University Contents 1 Three-Dimensional Space ....................................5 1.1 Rectangular Coordinates in R3 5 1.2 Dot Product7 1.3 Cross Product9 1.4 Lines and Planes 11 1.5 Parametric Curves 13 2 Partial Differentiations ....................................... 19 2.1 Functions of Several Variables 19 2.2 Partial Derivatives 22 2.3 Chain Rule 26 2.4 Directional Derivatives 30 2.5 Tangent Planes 34 2.6 Local Extrema 36 2.7 Lagrange’s Multiplier 41 2.8 Optimizations 46 3 Multiple Integrations ........................................ 49 3.1 Double Integrals in Rectangular Coordinates 49 3.2 Fubini’s Theorem for General Regions 53 3.3 Double Integrals in Polar Coordinates 57 3.4 Triple Integrals in Rectangular Coordinates 62 3.5 Triple Integrals in Cylindrical Coordinates 67 3.6 Triple Integrals in Spherical Coordinates 70 4 Vector Calculus ............................................ 75 4.1 Vector Fields on R2 and R3 75 4.2 Line Integrals of Vector Fields 83 4.3 Conservative Vector Fields 88 4.4 Green’s Theorem 98 4.5 Parametric Surfaces 105 4.6 Stokes’ Theorem 120 4.7 Divergence Theorem 127 5 Topics in Physics and Engineering .......................... 133 5.1 Coulomb’s Law 133 5.2 Introduction to Maxwell’s Equations 137 5.3 Heat Diffusion 141 5.4 Dirac Delta Functions 144 1 — Three-Dimensional Space 1.1 Rectangular Coordinates in R3 Throughout the course, we will use an ordered triple (x, y, z) to represent a point in the three dimensional space. -

Calculus Terminology
AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential -

Part IA — Vector Calculus
Part IA | Vector Calculus Based on lectures by B. Allanach Notes taken by Dexter Chua Lent 2015 These notes are not endorsed by the lecturers, and I have modified them (often significantly) after lectures. They are nowhere near accurate representations of what was actually lectured, and in particular, all errors are almost surely mine. 3 Curves in R 3 Parameterised curves and arc length, tangents and normals to curves in R , the radius of curvature. [1] 2 3 Integration in R and R Line integrals. Surface and volume integrals: definitions, examples using Cartesian, cylindrical and spherical coordinates; change of variables. [4] Vector operators Directional derivatives. The gradient of a real-valued function: definition; interpretation as normal to level surfaces; examples including the use of cylindrical, spherical *and general orthogonal curvilinear* coordinates. Divergence, curl and r2 in Cartesian coordinates, examples; formulae for these oper- ators (statement only) in cylindrical, spherical *and general orthogonal curvilinear* coordinates. Solenoidal fields, irrotational fields and conservative fields; scalar potentials. Vector derivative identities. [5] Integration theorems Divergence theorem, Green's theorem, Stokes's theorem, Green's second theorem: statements; informal proofs; examples; application to fluid dynamics, and to electro- magnetism including statement of Maxwell's equations. [5] Laplace's equation 2 3 Laplace's equation in R and R : uniqueness theorem and maximum principle. Solution of Poisson's equation by Gauss's method (for spherical and cylindrical symmetry) and as an integral. [4] 3 Cartesian tensors in R Tensor transformation laws, addition, multiplication, contraction, with emphasis on tensors of second rank. Isotropic second and third rank tensors. -

Chap. 8. Vector Differential Calculus. Grad. Div. Curl
Chap. 8. Vector Differential Calculus. Grad. Div. Curl 8.1. Vector Algebra in 2-Space and 3-Space - Scalar: a quantity only with its magnitude; temperature, speed, mass, volume, … - Vector: a quantity with its magnitude and its direction; velocity, acceleration, force, … (arrow & directed line segment) Initial and termination point Norm of a: length of a vector a. IaI =1: unit vector Equality of a Vectors: a=b: same length and direction. Components of a Vector: P(x1,y1,z1) Q(x2,y2,z2) in Cartesian coordinates. = = []− − − = a PQ x 2 x1, y2 y1,z2 z1 [a1,a 2 ,a3 ] = 2 + 2 + 2 Length in Terms of Components: a a1 a 2 a3 Position Vector: from origin (0,0,0) point A (x,y,z): r=[x,y,z] Vector Addition, Scalar Multiplication b (1) Addition: a + b = []a + b ,a + b ,a + b 1 1 2 2 3 3 a a+b a+ b= b+ a (u+ v) + w= u+ (v+ w) a+ 0= 0+ a= a a+ (-a) = 0 = [] (2) Multiplication: c a c a 1 , c a 2 ,ca3 c(a + b) = ca + cb (c + k) a = ca + ka c(ka) = cka 1a = a 0a = 0 (-1)a = -a = []= + + Unit Vectors: i, j, k a a1,a 2 ,a 3 a1i a 2 j a3 k i = [1,0,0], j=[0,1,0], k=[0,0,1] 8.2. Inner Product (Dot Product) Definition: a ⋅ b = a b cosγ if a ≠ 0, b ≠ 0 a ⋅ b = 0 if a = 0 or b = 0; cosγ = 0 3 ⋅ = + + = a b a1b1 a 2b2 a3b3 aibi i=1 a ⋅ b = 0 (a is orthogonal to b; a, b=orthogonal vectors) Theorem 1: The inner product of two nonzero vectors is zero iff these vectors are perpendicular. -

General Vector Calculus*
GENERALVECTOR CALCULUS* BY JAMES BYRNIE SHAW Introduction This paper presents results from various papers read before the Society during a period of several years. These are indicated in the footnotes. The calculus is independent of the number of dimensions of the space in which the vectors are supposed to be placed. Indeed the vectors are for the most part supposed to be imbedded in a space of an infinity of dimensions, this infinity being denumerable sometimes but more often non-denumerable. In the sense in which the term is used every vector is an infinite vector as regards its dimen- sionality. The reader may always make the development concrete by thinking of a vector as a function of one or more variables, usually one, and involving a parameter whose values determine the " dimensionality " of the space. The values the parameter can assume constitute its "spectrum." It must be emphasized however that no one concrete representation is all that is meant, for the vector is in reality an abstract entity given by its definition, that is to say, postulationally. The case is analogous to that of " group " in which the "operators" are generally not operators at all, since they have nothing to operate upon, but are abstract entities, defined by postulates. Always to interpret vectors as directed line-segments or as expansions of functions is to limit the generality of the subject to no purpose, and actually to interfere with some of the processes. It is sufficient to notice that in any case the theorems may be tested out in any concrete representation. -

Calculus III Refresher for Vector Calculus
Calculus III Refresher for Vector Calculus Jiˇr´ıLebl August 21, 2019 This class, Vector Calculus, is really the vector calculus that you haven't really gotten to in Calculus III. We will be using the book: H. M. Schey, Div, Grad, Curl, and All That: An Informal Text on Vector Calculus (Fourth Edition) Let us start with a very quick review of the concepts from Calculus III that we will need and that are not covered in Schey|a crash course if you will. We won't cover nearly everything that you may have seen in Calculus III in this quick overview, just the very basics. We will also go over a couple of things that you may not have seen in Calculus III, but that we will need for this class. You should look back at your Calculus III textbook. If you no longer have that or need another source, there is a wonderful free textbook: Gregory Hartman, APEX Calculus, http://www.apexcalculus.com. You can download a PDF online, or buy a very cheap printed copy. Especially Volume 3, that is, chapters 9{14. 1 Vectors In basic calculus, one deals with R, the real numbers, a one-dimensional space, or the line. In 2 vector calculus, we consider the two dimensional cartesian space R , the plane; three dimensional 3 n 2 3 n space R ; and in general the n-dimensional cartesian space R .A point in R ; R , or R is simply a tuple, a 3-tuple, or an n-tuple (respectively) of real numbers. For example, the following are points 2 in R (1; −2); (0; 1); (−1; 10); etc. -
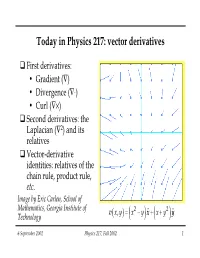
Today in Physics 217: Vector Derivatives
Today in Physics 217: vector derivatives First derivatives: • Gradient (—) • Divergence (—◊) •Curl (—¥) Second derivatives: the Laplacian (—2) and its relatives Vector-derivative identities: relatives of the chain rule, product rule, etc. Image by Eric Carlen, School of Mathematics, Georgia Institute of 22 vxyxy, =−++ x yˆˆ x y Technology ()()() 6 September 2002 Physics 217, Fall 2002 1 Differential vector calculus df/dx provides us with information on how quickly a function of one variable, f(x), changes. For instance, when the argument changes by an infinitesimal amount, from x to x+dx, f changes by df, given by df df= dx dx In three dimensions, the function f will in general be a function of x, y, and z: f(x, y, z). The change in f is equal to ∂∂∂fff df=++ dx dy dz ∂∂∂xyz ∂∂∂fff =++⋅++ˆˆˆˆˆˆ xyzxyz ()()dx() dy() dz ∂∂∂xyz ≡⋅∇fdl 6 September 2002 Physics 217, Fall 2002 2 Differential vector calculus (continued) The vector derivative operator — (“del”) ∂∂∂ ∇ =++xyzˆˆˆ ∂∂∂xyz produces a vector when it operates on scalar function f(x,y,z). — is a vector, as we can see from its behavior under coordinate rotations: I ′ ()∇∇ff=⋅R but its magnitude is not a number: it is an operator. 6 September 2002 Physics 217, Fall 2002 3 Differential vector calculus (continued) There are three kinds of vector derivatives, corresponding to the three kinds of multiplication possible with vectors: Gradient, the analogue of multiplication by a scalar. ∇f Divergence, like the scalar (dot) product. ∇⋅v Curl, which corresponds to the vector (cross) product. ∇×v 6 September 2002 Physics 217, Fall 2002 4 Gradient The result of applying the vector derivative operator on a scalar function f is called the gradient of f: ∂∂∂fff ∇f =++xyzˆˆˆ ∂∂∂xyz The direction of the gradient points in the direction of maximum increase of f (i.e. -

Supersymmetric Quantum Mechanics and Morse Theory
Supersymmetric Quantum Mechanics and Morse Theory by Vyacheslav Lysov Okinawa Institute for Science and Technology Homework 3: d = 0 Ssupersymmetry Due date: July 13 1 Linking number Introduction: For pair of loops (curve with no boundary) C1 and C2, given in parametric form 1 3 i 1 3 i C1 = S ! R : t 7! γ1(t);C2 = S ! R : t 7! γ2(t) (1.1) the formula for the linking number is well known Z 2π Z 2π i j k 1 X ijkγ_ 1(t1)_γ2(t2)(γ1(t1) − γ2(t2)) lk(C1;C2) = dt1 dt2 3 : (1.2) 4π jγ1(t1) − γ2(t2)j 0 0 ijk On the lecture we briefly discussed the relation between the linking number and intersection number. The goal of this problem is to derive the formula above from the intersection theory. Construction: The Poincare lemma for R3 implies that 3 1 3 H1(R ) = H (R ) = 0; (1.3) so for any loop C ⊂ R3 there exists a surface S ⊂ R3 such that @S = C: (1.4) 3 For two loops C1 and C2 in R we can define linking number via the intersection number lk(C1;C2) = C1 · S; (1.5) where S is surface, homotopic to a disc, such that @S = C2. We can use the integral formula for the intersection number Z C · S = ηC ^ ηS: (1.6) R3 The 1-form ηC is defined via Z Z 1 3 ! = ηC ^ !; 8! 2 Ω (R ): (1.7) C R3 The Poincare dual form ηC for loop C is trivial in cohomology 2 3 [ηC ] = 0 2 H (R ) = 0; (1.8) 1 hence we can write it as ηC = dηS: (1.9) Formally, the 1-form ηS is given by −1 ηS = d ηC ; (1.10) but the inverse of external derivative is not a differential operator on forms. -

Chapter 1 Vector Calculus
Chapter 1 vector calculus Vector calculus is the study of vector fields and related scalar functions. For the most part we focus our attention on two or three dimensions in this study. However, certain theorems are easily n extended to R . We explore these concepts in both Cartesian and the standard curvelinear coor- diante systems. I also discuss the dictionary between the notations popular in math and physics 1 The importance of vector calculus is nicely exhibited by the concept of a force field in mechanics. For example, the gravitational field is a field of vectors which fills space and somehow communi- cates the force of gravity between massive bodies. Or, in electrostatics, the electric field fills space and somehow communicates the influence between charges; like charges repel and unlike charges attract all through the mechanism propagated by the electric field. In magnetostatics constant magnetic fields fill space and communicate the magnetic force between various steady currents. All the examples above are in an important sense static. The source charges2 are fixed in space and they cause a motion for some test particle immersed in the field. This is an idealization. In truth, the influence of the test particle on the source particle cannot be neglected, but those sort of interactions are far too complicated to discuss in elementary courses. Often in applications the vector fields also have some time-dependence. The differential and inte- gral calculus of time-dependent vector fields is not much different than that of static fields. The main difference is that what was once a constant is now some function of time. -

Corral's Vector Calculus
1 0.8 0.6 0.4 0.2 z 0 -0.2 -10 -0.4 -5 -10 0 -5 x 0 5 5 y 10 10 CORRAL’S VECTOR CALCULUS Michael Corral and Anton Petrunin Corral’s Vector Calculus Michael Corral and Anton Petrunin About the author: Michael Corral is an Adjunct Faculty member of the Department of Mathematics at Schoolcraft College. He received a B.A. in Mathematics from the University of California at Berkeley, and received an M.A. in Mathematics and an M.S. in Industrial & Operations Engineering from the University of Michigan. This text was typeset in LATEX2ε with the KOMA-Script bundle, using the GNU Emacs text editor on a Fedora Linux system. The graphics were created using MetaPost, PGF, and Gnuplot. Copyright ©2016 Anton Petrunin. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version published by the Free Software Foundation; with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts. A copy of the license is included in the section entitled “GNU Free Documentation License”. Preface This book covers calculus in two and three variables. It is suitable for a one-semester course, normally known as “Vector Calculus”, “Multivariable Calculus”, or simply “Calculus III”. The prerequisites are the standard courses in single-variable calculus (also known as Cal- culus I and II). The exercises are divided into three categories: A, B and C. The A exercises are mostly of a routine computational nature, the B exercises are slightly more involved, and the C exercises usually require some effort or insight to solve.