Comparing and Forecasting Performances in Different Events of Athletics Using a Probabilistic Model
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Lausanne 2016: Long Jump W
Women's Long Jump Diamond Race 25.08.2016 Start list Long Jump Time: 21:00 Records Order Athlete Nat NR PB SB 1 Blessing OKAGBARE-IGHOTEGUONOR NGR 7.12 7.00 6.73 WR 7.52 Galina CHISTYAKOVA URS Leningrad 11.06.88 2 Christabel NETTEY CAN 6.99 6.99 6.75 AR 7.52 Galina CHISTYAKOVA URS Leningrad 11.06.88 NR 6.84 Irene PUSTERLA SUI Chiasso 20.08.11 3 Akela JONES BAR 6.75 6.75 6.75 WJR 7.14 Heike DRECHSLER GDR Bratislava 04.06.83 4 Lorraine UGEN GBR 7.07 6.92 6.76 MR 7.48 Heike DRECHSLER GER 08.07.92 5 Shara PROCTOR GBR 7.07 7.07 6.80 DLR 7.25 Brittney REESE USA Doha 10.05.13 6 Darya KLISHINA RUS 7.52 7.05 6.84 SB 7.31 Brittney REESE USA Eugene 02.07.16 7 Ivana SPANOVIĆ SRB 7.08 7.08 7.08 8 Tianna BARTOLETTA USA 7.49 7.17 7.17 2016 World Outdoor list 7.31 +1.7 Brittney REESE USA Eugene 02.07.16 7.17 +0.6 Tianna BARTOLETTA USA Rio de Janeiro 17.08.16 Medal Winners Diamond Race 7.16 +1.6 Sosthene MOGUENARA GER Weinheim 29.05.16 1 Ivana SPANOVIĆ (SRB) 36 7.08 +0.6 Ivana SPANOVIĆ SRB Rio de Janeiro 17.08.16 2016 - Rio de Janeiro Olympic Games 2 Brittney REESE (USA) 16 7.05 +2.0 Brooke STRATTON AUS Perth 12.03.16 1. Tianna BARTOLETTA (USA) 7.17 3 Christabel NETTEY (CAN) 15 6.95 +0.6 Malaika MIHAMBO GER Rio de Janeiro 17.08.16 2. -
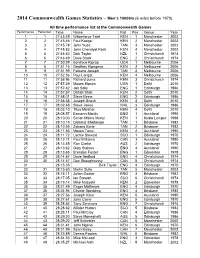
2014 Commonwealth Games Statistics – Men's
2014 Commonwealth Games Statistics – Men’s 10000m (6 miles before 1970) All time performance list at the Commonwealth Games Performance Performer Time Name Nat Pos Venue Year 1 1 27:45.39 Wilberforce Talel KEN 1 Manchester 2002 2 2 27:45.46 Paul Kosgei KEN 2 Manchester 2002 3 3 27:45.78 John Yuda TAN 3 Manchester 2002 4 4 27:45.83 John Cheruiyot Korir KEN 4 Manchester 2002 5 5 27:46.40 Dick Taylor NZL 1 Christchurch 1974 6 6 27:48.49 Dave Black ENG 2 Christchurch 1974 7 7 27:50.99 Boniface Kiprop UGA 1 Melbourne 2006 8 8 27:51.16 Geoffrey Kipngeno KEN 2 Melbourne 2006 9 9 27:51.99 Fabiano Joseph TAN 3 Melbourne 2006 10 10 27:52.36 Paul Langat KEN 4 Melbourne 2006 11 11 27:56.96 Richard Juma KEN 3 Christchurch 1974 12 12 27:57.39 Moses Kipsiro UGA 1 Delhi 2010 13 13 27:57.42 Jon Solly ENG 1 Edinburgh 1986 14 14 27:57.57 Daniel Salel KEN 2 Delhi 2010 15 15 27:58.01 Steve Binns ENG 2 Edinburgh 1986 16 16 27:58.58 Joseph Birech KEN 3 Delhi 2010 17 17 28:02.48 Steve Jones WAL 3 Edinburgh 1986 18 18 28:03.10 Titus Mbishei KEN 4 Delhi 2010 19 19 28:08.57 Eamonn Martin ENG 1 Auckland 1990 20 20 28:10.00 Simon Maina Munyi KEN 1 Kuala Lumpur 1998 21 21 28:10.15 Gidamis Shahanga TAN 1 Brisbane 1982 22 22 28:10.55 Zakaria Barie TAN 2 Brisbane 1982 23 23 28:11.56 Moses Tanui KEN 2 Auckland 1990 24 24 28:11.72 Lachie Stewart SCO 1 Edinburgh 1970 25 25 28:12.71 Paul Williams CAN 3 Auckland 1990 25 26 28:13.45 Ron Clarke AUS 2 Edinburgh 1970 27 27 28:13.62 Gary Staines ENG 4 Auckland 1990 28 28 28:13.65 Brendan Foster ENG 1 Edmonton 1978 29 29 28:14.67 -

Women's 3000M Steeplechase
Games of the XXXII Olympiad • Biographical Entry List • Women Women’s 3000m Steeplechase Entrants: 47 Event starts: August 1 Age (Days) Born SB PB 1003 GEGA Luiza ALB 32y 266d 1988 9:29.93 9:19.93 -19 NR Holder of all Albanian records from 800m to Marathon, plus the Steeplechase 5000 pb: 15:36.62 -19 (15:54.24 -21). 800 pb: 2:01.31 -14. 1500 pb: 4:02.63 -15. 3000 pb: 8:52.53i -17, 8:53.78 -16. 10,000 pb: 32:16.25 -21. Half Mar pb: 73:11 -17; Marathon pb: 2:35:34 -20 ht EIC 800 2011/2013; 1 Balkan 1500 2011/1500; 1 Balkan indoor 1500 2012/2013/2014/2016 & 3000 2018/2020; ht ECH 800/1500 2012; 2 WSG 1500 2013; sf WCH 1500 2013 (2015-ht); 6 WIC 1500 2014 (2016/2018-ht); 2 ECH 3000SC 2016 (2018-4); ht OLY 3000SC 2016; 5 EIC 1500 2017; 9 WCH 3000SC 2019. Coach-Taulant Stermasi Marathon (1): 1 Skopje 2020 In 2021: 1 Albanian winter 3000; 1 Albanian Cup 3000SC; 1 Albanian 3000/5000; 11 Doha Diamond 3000SC; 6 ECP 10,000; 1 ETCh 3rd League 3000SC; She was the Albanian flagbearer at the opening ceremony in Tokyo (along with weightlifter Briken Calja) 1025 CASETTA Belén ARG 26y 307d 1994 9:45.79 9:25.99 -17 Full name-Belén Adaluz Casetta South American record holder. 2017 World Championship finalist 5000 pb: 16:23.61 -16. 1500 pb: 4:19.21 -17. 10 World Youth 2011; ht WJC 2012; 1 Ibero-American 2016; ht OLY 2016; 1 South American 2017 (2013-6, 2015-3, 2019-2, 2021-3); 2 South American 5000 2017; 11 WCH 2017 (2019-ht); 3 WSG 2019 (2017-6); 3 Pan-Am Games 2019. -

Anti-Black Racism and the Foreign Black Other: Constructing Blackness and the Sporting Migrant
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Illinois Digital Environment for Access to Learning and Scholarship Repository ANTI-BLACK RACISM AND THE FOREIGN BLACK OTHER: CONSTRUCTING BLACKNESS AND THE SPORTING MIGRANT BY MUNENE FRANJO MWANIKI DISSERTATION Submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Sociology in the Graduate College of the University of Illinois at Urbana-Champaign, 2014 Urbana, Illinois Doctoral Committee: Associate Professor Margaret Kelley, Chair Professor Tim Liao Associate Professor Moon-Kie Jung Associate Professor Monica McDermott ABSTRACT The popularity and globalization of sport has led to an ever-increasing black athletic labor migration from the global South to, primarily, the U.S. and Western European countries. While the hegemonic ideology surrounding sport is that it brings different people together and ameliorates social boundaries, sociologists of sport have shown this to be a gross simplification. Instead, sport is often seen to reinforce and recreate social stereotypes and boundaries, especially as it regards race and the black athlete in body and culture. At best we can think of sport as a contested terrain for both maintaining and challenging racial norms and boundaries. The mediated black athlete has thus always, for better or worse, impacted popular white perceptions of blackness broadly and globally. While much work has been done to expose the workings of race and racism in sport, studies have tended to homogenize black populations and have not taken into account the varying histories and complexities of, specifically, black African migrant athletes. -

Pole Vault Promotional 04.07.2019
Women's Pole Vault Promotional 04.07.2019 Start list Pole Vault Time: 18:30 Records Order Athlete Nat NR PB SB 1 Nicole BÜCHLER SUI 4.78 4.78 4.41 WR 5.06 Yelena ISINBAYEVA RUS Zürich 28.08.09 2 Angelica MOSER SUI 4.78 4.61 4.55 AR 5.06 Yelena ISINBAYEVA RUS Zürich 28.08.09 3 Holly BRADSHAW GBR 4.81 4.81 4.57 NR 4.78 Nicole BÜCHLER SUI Doha 06.05.16 WJR 4.71 Wilma MURTO FIN Zweibrücken 31.01.16 4 Robeilys PEINADO VEN 4.70 4.70 4.67 MR 4.93 Yelena ISINBAYEVA RUS 05.07.05 5 Katie NAGEOTTE USA 5.00 4.80 4.67 DLR 5.00 Sandi MORRIS USA Bruxelles 09.09.16 6 Yarisley SILVA CUB 4.91 4.91 4.67 SB 4.91 Jennifer SUHR USA Austin, TX 30.03.19 7 Michaela MEIJER SWE 4.76 4.71 4.70 8 Katerina STEFANIDI GRE 4.91 4.91 4.72 9 Alysha NEWMAN CAN 4.76 4.76 4.76 2019 World Outdoor list 10 Anzhelika SIDOROVA ANA 4.85 4.77 4.91 Jennifer SUHR USA Austin, TX 30.03.19 4.85 Eliza MCCARTNEY NZL Hastings 26.01.19 Progression: 4.22 - 4.37 - 4.47 - 4.57 - 4.67 - 4.72 - 4.77 - 4.82 - 4.87 4.82 Sandi MORRIS USA Rabat 16.06.19 4.77 Anzhelika SIDOROVA ANA Rabat 16.06.19 4.76 Angelica BENGTSSON SWE Roma 06.06.19 4.76 Alysha NEWMAN CAN Guelph 07.06.19 4.73 Olivia GRUVER USA Palo Alto, CA 29.03.19 Medal Winners Lausanne previous 4.72 Katerina STEFANIDI GRE Shanghai 18.05.19 Winners 4.72 Ling LI CHN Shanghai 18.05.19 2018 - Berlin European Ch. -

Sebastian Coe IAAF President * Paris Staged the ‘World Indoor Games’ in 1985 2
President’s Message IAAF World Indoor Championships Global support for IAAF World Indoor health, the environment, Portland 2016 Championships, Portland social inclusion and peace. 2016 The IAAF World Indoor Powered by Championships are the most important IAAF World Athletics Series competition after the outdoor world championships. Progress Report to IAAF Council Portland marks a welcome November 2015 return of the world indoors to the United States of America. In 1987 Indianapolis, USA played host to the inaugural edition of the IAAF World Indoor Championships*. Since then there have been non- stadia events (race walking and cross country) and a wonderful world juniors in 2014. The IAAF World Indoor Championships, Portland 2016 therefore represent the most significant IAAF World Athletics Series competition to be hosted in the USA in three decades. The USA is historically the strongest athletics nation as measured by overall participation and the medals won by its athletes. Many of the legends of our sport are American. USA, the world’s first economic power, is a heartland of our sport yet general public perception of track and field athletics is low. The IAAF World Indoor Championships, Portland 2016 (17-20 March 2016) in the Oregon Convention Center will do much to raise awareness in America. Aside from the Rio Olympic Games these championships are the most important athletics event in 2016. I look forward with great anticipation to joining the athletes, coaches, officials, media and fans from around 150 nations in Portland. Sebastian -

List of All Olympics Winners in Ethiopia
Location Year Player Sport Medals Event Results London 2012 Tariku BEKELE Athletics Bronze 10000m 27:31.4 London 2012 Tirunesh DIBABA Athletics Gold 10000m 30:20.8 London 2012 Sofia ASSEFA Athletics Bronze 3000m steeplechase 09:09.8 London 2012 Tirunesh DIBABA Athletics Bronze 5000m 15:05.2 London 2012 Meseret DEFAR Athletics Gold 5000m 15:04.3 London 2012 Dejen GEBREMESKEL Athletics Silver 5000m 13:42.0 London 2012 Tiki GELANA Athletics Gold marathon 02:23:07 Beijing 2008 Sileshi SIHINE Athletics Silver 10000m 27:02.77 Beijing 2008 Tirunesh DIBABA Athletics Gold 10000m 29:54.66 Beijing 2008 Kenenisa BEKELE Athletics Gold 10000m 27:01.17 Beijing 2008 Meseret DEFAR Athletics Bronze 5000m 15:44.1 Beijing 2008 Tirunesh DIBABA Athletics Gold 5000m 15:41.4 Beijing 2008 Kenenisa BEKELE Athletics Gold 5000m 12:57.82 Beijing 2008 Tsegay KEBEDE Athletics Bronze marathon 2h10:00 Athens 2004 Sileshi SIHINE Athletics Silver 10000m 27:09.4 Athens 2004 Derartu TULU Athletics Bronze 10000m 30:26.4 Athens 2004 Kenenisa BEKELE Athletics Gold 10000m 27:05.1 Athens 2004 Ejegayehu DIBABA Athletics Silver 10000m 30:25.0 Athens 2004 Tirunesh DIBABA Athletics Bronze 5000m 14:51.8 Athens 2004 Meseret DEFAR Athletics Gold 5000m 14:45.7 Athens 2004 Kenenisa BEKELE Athletics Silver 5000m 13:14.6 Sydney 2000 Gete WAMI Athletics Silver 10000m 30:22.5 Sydney 2000 Haile GEBRSELASSIE Athletics Gold 10000m 27:18.2 Sydney 2000 Derartu TULU Athletics Gold 10000m 30:17.5 Sydney 2000 Assefa MEZGEBU Athletics Bronze 10000m 27:19.7 Sydney 2000 Millon WOLDE Athletics Gold 5000m -

2016 Olympic Games Statistics – Men's 10000M
2016 Olympic Games Statistics – Men’s 10000m by K Ken Nakamura Record to look for in Rio de Janeiro: 1) Last time KEN won gold at 10000m is back in 1968. Can Kamworor, Tanui or Karoki change that? 2) Can Mo Farah become sixth runner to win back to back gold? Summary Page: All time Performance List at the Olympic Games Performance Performer Time Name Nat Pos Venue Year 1 1 27:01.17 Kenenisa Bekele ETH 1 Beijing 2008 2 2 27:02.77 Sileshi Sihine ETH 2 Beijing 2008 3 3 27:04.11 Micah Kogo KEN 3 Beijing 2008 4 4 27:04.11 Moses Masai KEN 4 Beijing 2008 5 27:05.10 Kenenisa Bekele 1 Athinai 2004 6 5 27:05.11 Zersenay Tadese ERI 5 Beijing 2008 7 6 27:06.68 Haile Gebrselassie ETH 6 Beijing 2008 8 27:07.34 Haile Gebrselassie 1 Atlanta 1996 Slowest winning time since 1972: 27:47.54 by Alberto Cova (ITA) in 1984 Margin of Victory Difference Winning time Name Nat Venue Year Max 47.8 29:59.6 Emil Zatopek TCH London 1948 18.68 27:47.54 Alberto Cova ITA Los Angeles 1984 Min 0.09 27:18.20 Haile Gebrselassie ETH Sydney 2000 Second line is largest margin since 1952 Best Marks for Places in the Olympics Pos Time Name Nat Venue Year 1 27:01.17 Kenenisa Bekele ETH Beijing 2008 2 27:02.77 Sileshi Sihine ETH Beijing 2008 3 27:04.11 Micah Kogo KEN Beijing 2008 4 27:04.11 Moses Masai KEN Beijing 2008 5 27:05.11 Zersenay Tadese ERI Beijing 2008 6 27:06.68 Haile Gebrselassie ETH Beijing 2008 7 27:08.25 Martin Mathathi KEN Beijing 2008 Multiple Gold Medalists: Kenenisa Bekele (ETH): 2004, 2008 Haile Gebrselassie (ETH): 1996, 2000 Lasse Viren (FIN): 1972, 1976 Emil -

3D Biomechanical Analysis of Women's High Jump Technique
STUDY VIEWPOINT© by IAAF 3D Biomechanical Analysis 27:3; 31-44, 2012 of Women’s High Jump Technique by Vassilios Panoutsakopoulos and Iraklis A. Kollias ABSTRACT AUTHORS The purpose of the present study was to in- Vassilios Panoutsakopoulos is a PhD Can- vestigate the three-dimensional kinemat- didate in Biomechanics. He teaches Track ics of contemporary high jump technique and Field in the Department of Physical during competition and to compare the re- Education & Sports Science, Aristotle Uni- sults with findings from previous elite-level versity of Thessaloniki, Greece. events. The participants in the women’s high jump event of the European Athlet- Prof. Dr. Iraklis A. Kollias is the Director of ics Premium Meeting “Thessaloniki 2009” the Biomechanics Laboratory of the De- served as subjects. The jumps were re- partment of Physical Education & Sports corded using three stationary digital video Science, Aristotle University of Thessalon- cameras, operating at a sampling frequen- iki, Greece. His major fields of research are cy of 50fields/sec. The kinematic param- the 3D analysis of sports technique and the eters of the last two strides, the take-off development of specific instrumentation and the bar clearance were extracted for for sport analysis. analysis through software. The results in- dicated that the kinematic parameters of the approach (i.e. horizontal velocity, stride length, stride angle, height of body centre Introduction of mass) were similar to those reported in the past. However, a poor transformation urrently, most top high jumpers use of horizontal approach velocity to vertical one of the versions of the Fosbury take-off velocity was observed as a greater C Flop technique1. -

Yelena Isinbayeva
www.FAMOUS PEOPLE LESSONS.com YELENA ISINBAYEVA http://www.famouspeoplelessons.com/y/yelena_isinbayeva.html CONTENTS: The Reading / Tapescript 2 Synonym Match and Phrase Match 3 Listening Gap Fill 4 Choose the Correct Word 5 Spelling 6 Put the Text Back Together 7 Scrambled Sentences 8 Discussion 9 Student Survey 10 Writing 11 Homework 12 Answers 13 YELENA ISINBAYEVA THE READING / TAPESCRIPT Yelena Isinbayeva is the greatest female pole vaulter ever. She won the 2004 and 2008 Olympic Gold Medal and has twice been the IAAF’s Female Athlete of the Year. In 2005, she became the first woman to clear five metres and is the current world record holder. Isinbayeva is also an avid reader of Russian history and a collector of dolphins – both model and real. Isinbayeva was born in Volgograd, Russia in 1982. From the age of five, she trained as a gymnast. However, she quit the sport when she was 15 because at 1.74 metres she was too tall. She loved competition and switched to pole vaulting. Her first big competition was the 1998 World Junior Championships, where she finished ten centimeters outside the medals. Isinbayeva showed her true potential in 1999 at the World Youth Games in Poland. She cleared 4.10m to take her very first gold medal. She would improve by nearly one metre over the next decade. In 2000, she won gold again at the Youth Games and the European Junior Championships In 2003, Yelena burst onto the world stage when she broke the world record, clearing 4.82m at a meeting in England. -

Olympic Games Day 1 Olympics Summer Winter Aniket Pawar Special/Paralympics Youth the Original Greek Games
Olympic Games Day 1 Olympics Summer Winter Aniket Pawar Special/Paralympics Youth The Original Greek Games began in ancient Greece took place every fourth year for several hundred years. The earliest record of the Olympic Games goes back to776 BC. The Original Olympics The only event was a foot race of about 183 meters. They also included competitions in music, oratory and theatre performances. The 18-th Olympics Included wrestling and pentathlon, later Games – chariot races and other sports. In 394 A.D. the games were ended by the Roman emperor Theodosius. Pierre de Coubertin Brought the Olympic Games back to life in 1896. SPORTS IN SUMMER OLYMPICS • The current categories are: ▫ Category A: athletics, aquatics, gymnastics.3 ▫ Category B: basketball, cycling, football, tennis, and volleyball.5 ▫ Category C: archery, badminton, boxing, judo, rowing, shooting, table tennis, and weightlifting.8 ▫ Category D: canoe/kayaking, equestrian, fencing, handball, field hockey, sailing, taekwondo, triathlon, and wrestling.9 ▫ Category E: modern pentathlon, golf, and rugby.3 WINTER OLYMPIC GAMES • held every four years. • The athletes compete in 20 different disciplines (including 5 Paralympics' disciplines). Founder & Beginning • The foundation for the Winter Olympics are Nordic games. • Gustav Viktor Balck - organizer of the Nordic games and a member of the IOC. • The first Summer Olympics with winter sport were in London, in 1908. The first ‘winter sports week’ was planned in 1916, in Berlin, but the Olympics were cancelled because of the outbreak of the World War I. The first true Winter Olympics were in 1924, in Chamonix, France. • In 1986, the IOC decided to separate the Summer and Winter Games on separate years. -

10000 Meters
2020 Olympic Games Statistics - Women’s 10000m by K Ken Nakamura The records to look for in Tokyo: 1) Kenyan woman never won the W10000m in the OG. Will H Obiri be the first? 2) Showdown between Hassan & Gidey. Can Hassan become first from NED to win the Olympic 10000m? 3) Can Tsehay Gemechu become second (after Tulu) All African Games champion to win the Olympics. 4) Can Gezahegne win first medal for BRN? 5) Can Eilish McColgan become second GBR runner (after Liz, her mother) to win an Olympic medal? Summary Page: All time Performance List at the Olympic Games Performance Performer Time Name Nat Pos Venue Year 1 1 29:17.45 Almaz Ayana ETH 1 Rio de Janeiro 2016 2 2 29:32.53 Vivian Cheruiyot KEN 2 Rio de Jane iro 2016 3 3 29:42.56 Tirunesh Dibaba ETH 3 Rio de Janeiro 2016 4 4 29:53.51 Al ice Aprot Nawowuna KEN 4 Rio de Janeiro 2016 5 29:54.66 Tirunesh Dibaba ETH 1 Beijing 2008 6 5 30:07.78 Betsy Sa ina KE N 5 Rio de Jane iro 2016 7 6 30 :13.17 Molly Huddle USA 6 Rio de Jan eiro 2016 8 7 30:17.49 Derartu Tulu ETH 1 Sydney 2000 Slowest winning time: 31:06.02 by Derartu Tulu (ETH) in 1992 Margin of Victory Difference Winning time Name Nat Venue Year Max 15.08 29:17.45 Alm az Ayana ETH Rio de Janeiro 2016 5.73 31:06.02 Derartu Tulu ETH Barcelona 1992 Min 0.62 30:24.36 Xing Huina CHN Athinai 2004 Best Marks for Places in the Olympics Pos Time Name Nat Venue Year 1 29:17.45 Almaz Ayana ETH Rio de Janeiro 2016 29:54.66 Ti runesh Dibaba ETH Beijing 2008 2 29:32.53 Vivian Cheruiyot KEN Rio de Janeiro 2016 30:22.22 Shalane Flanagan USA Beijing 2008