DOCSLIB.ORG

Optical Cloaking of a Cylindrical Shape

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Optical Cloaking of a Cylindrical Shape Optical Cloaking of a Spherical Shape Creating an Illusion of Invisibility using Metamaterials April 1, 2010 Optical Cloaking Authors: Amanda Booth David Dror Daniel Frasquillo Jaron Gubernick With thanks to Dr. Gabitov for his help. Our goal: To explore mathematical methods that have been previously constructed that successfully model the cloaking of objects, otherwise known as invisibility. To do this the use of metamaterials is necessary; therefore an understanding of metamaterials is required to convert our mathematical model back into English for practical applications. We also wish to explore other applications for metamaterials, such as optical black holes. Why should we care? Invisibility has been the realm of myth for so long that it would be a clear triumph of science to be able to make something macroscopic invisible. Military applications would include avoiding detection through radar or from regular visible light. The better we understand how to control light, the better telescopes, detectors, and other optical instruments we can create. Some materials and records decay in the presence of light. Making these objects ‘invisible’ would shield them from the light and preserve them. What has been done? Dr. John Pendry, a physicist, has developed mathematical methods using metamaterials to produce cloaking devices. Graduate students at the University of Arizona have also worked on the theory presented by Pendry. Previous Work Metamaterials are artificially engineered materials that produce unusual optical properties, Metamaterials namely negative refractive indices. At the moment, most of the success at making these materials are for radio waves or individual wavelengths of visible light. It is interesting to note that metamaterials do not occur anywhere in nature!! Scanning electron microscope image of a metamaterial developed for microwaves Where did the idea for metamaterials originate? Scientists first observed materials reflecting light in a unique way in nature. The Blue Morpho Butterfly utilizes iridescence in its wings to reflect blue light from its surroundings. For years, people were trying to extract dye from these butterflies until they realized the stunning color exists from microscopic scales in the wings that reflect incident light in successive layers. Observations like this may have lead to an increased study in light wave refraction. Interpretation of Metamaterials Mathematicians observed that for a material with an index of refraction, n may be represented by the term n2 = εμ, where ε is the dielectric constant, and μ is the magnetic permeability. Solving for n yields two solutions, one positive and one negative. Scientists wanted to create a material that has a negative n solution. It was only by knowing such a solution was possible and then attempting to recreate it through experimenting with various ε and μ’s that metamaterials were actually discovered. Snell’s Law η1sinθI= η2sinθT This is the formula for the angle of refraction of light (using the symbols in the image to the right). η1, η2 are the refractive indices of the two materials and θI, θT are the angles between the ray of light and the normal . Negative Refractive Index The ‘rays’ in the 4th quadrant give examples of how common materials affect light. The 3rd quadrant provides an illustration of how metamaterials refract the light. The deflection of the incoming light ray is given by Snell’s law : η1sinθI= η2sinθT . It is fairly straightforward to see that if η2 is negative, then the angle of refraction will be the opposite of conventional refraction. Negative Refractive Index Another effect of negative http://people.ee.duke.edu/~drsmit refractive index is that is makes h/negative_index_about.htm the waves inside of a pulse flow in the opposite direction from the pulse itself. The math for this can be seen from the formula for the speed of light in a medium: v = c / n . V is speed of light in the medium, c is speed of light in vacuum, and n is index of refraction. It is clear that if n is negative, v is negative too. We are using metamaterials to make rays of light refract around the object and then convene to their original course once on the other side. Maxwell’s Equations It is important to understand the significance of Maxwell’s equations relating to the problem at hand. Since the equations are applicable under ×E=-μ(r)μ0∂H/∂t coordinate transformations, × any shape can be modeled as ∇ H=+ε(r)ε0∂E/∂t long as the proper coordinate ∇where μ(r) represents transformation can be the magnetic determined: permeability and ε(r) is the electrical permittivity. One way to look at the How did we effects of refraction is by using coordinate model invisibility? transformations instead of refraction explicitly. As you can see on the left, as the light passes through a different set of coordinates it continues to travel in a straight line, but what looks straight inside the local coordinates looks bent from the outside. Why do we need metamaterials for invisibility? We need an index of refraction that changes in a continuous controlled manner, and our only understanding of how to do this is through the use of metamaterials. What we did: The paper we used (Pendry et al), actually explicitly states a straightforward coordinate transformation to cloak a sphere. If the new coordinates are r’, θ’ and φ’ , and the sphere we are trying to cloak has a radius R1, and the cloak surrounding the sphere has a radius R2 the coordinate transformation to cloak a sphere is: r’ = (R2-R1)*r/R2 + R1 θ’ = θ φ’ = φ We applied this transformation to simulated rays of light (3-D ‘straight’ lines) in a specific situation where R1 = .5 and R2 =1, and found that it worked as claimed; the sphere almost never got touched by the light. Pictures! Transforming these equations under spherical coordinates yields: r′ r′ 2 ε′ = μ′ = [R2/(R2-R1)][(r′-R1)/r′] , (9) for R1 > r′> R2 Or, for our specific case: ε′r′= μ′r′= 2(.5r/(.5r+.5))^2 θ′ θ′ ϕ′ ϕ′ ε′ = μ′ = ε′ = μ′ = R2/(R2-R1) = 2 (10) where R1 is the inner radius and contains the object and R2 is the outer radius. The waves must only distort the coordinate grid where R1 < r < R2, so this is the only region affected by the different μ and ε values described in equations 9 and 10. By determining the values for μ(r) and ε(r), the properties for designing a metamaterial may be specified. What we learned: The rays actually did not get bent if the were coming in straight through the center of the sphere. The reason for this is that the angle of the light (both θ and φ) would not change over the course of this transformation, and so all the transformation would do is effect the rate at which the light gets to the center. The above effect does not actually matter in practice because the percentage of light that is coming in perfectly through the center in real life is infinitely small, and therefore would not be visible. Difficulties for Invisibility in Real Applications Manipulating the previous set of equations, in order to achieve invisibility we need a index of refraction varying continuously between 2/9 and 1/2. The issue is, even though metamaterials are produced in the lab, those that effect visible light only effect a narrow portion of the wavelengths in the correct way. This means the object might become invisible to green light but not to red or blue. Work is still being done from the practical end to make what we modeled possible. A lot of shapes in real life are not spheres. The coordinate transformations and therefore the configuration of the materials for non-spherical shapes in much more difficult. Where do we go from here? Modeling non-spherical shapes, particularly something that might be able to cover a human being: say a cylinder with a half sphere on top. Figuring out how to focus light at a specific point (used in lensing, various instruments, and potentially even a way to make solar power more efficient.) Determining, from observing model behavior, where some difficulties might arise putting this into practice. Where do we go from here? We plan on expanding the idea we have of cloaking a sphere and making it into a shape similar to that of a cylinder/hemisphere combination Optical Black Holes This is an example of redirection of light rays due to a negative index of refraction may present possibilities for optical black holes Optical black holes redirect all incoming light to a single point, causing potential for highly effective generation of light energy into solar energy, for example Work in progress References: Pendry,John.Taking the wraps off cloaking. The Blackett Laboratory, Department of Physics, Imperial College London, London SW7 2AZ, UK. Physics 2, 95 (2009). http://www.dailymotion.com/video/x6jvnm_lecture-john- pendry-invisibility-cl_tech Crosskey M., Nixon A., & Schick L. Invisibility in Metamaterials: Transformations and Ray Tracing. June 26, 2009..
Load more

Recommended publications
  • Glossary Physics (I-Introduction)
    1 Glossary Physics (I-introduction) - Efficiency: The percent of the work put into a machine that is converted into useful work output; = work done / energy used [-]. = eta In machines: The work output of any machine cannot exceed the work input (<=100%); in an ideal machine, where no energy is transformed into heat: work(input) = work(output), =100%. Energy: The property of a system that enables it to do work. Conservation o. E.: Energy cannot be created or destroyed; it may be transformed from one form into another, but the total amount of energy never changes. Equilibrium: The state of an object when not acted upon by a net force or net torque; an object in equilibrium may be at rest or moving at uniform velocity - not accelerating. Mechanical E.: The state of an object or system of objects for which any impressed forces cancels to zero and no acceleration occurs. Dynamic E.: Object is moving without experiencing acceleration. Static E.: Object is at rest.F Force: The influence that can cause an object to be accelerated or retarded; is always in the direction of the net force, hence a vector quantity; the four elementary forces are: Electromagnetic F.: Is an attraction or repulsion G, gravit. const.6.672E-11[Nm2/kg2] between electric charges: d, distance [m] 2 2 2 2 F = 1/(40) (q1q2/d ) [(CC/m )(Nm /C )] = [N] m,M, mass [kg] Gravitational F.: Is a mutual attraction between all masses: q, charge [As] [C] 2 2 2 2 F = GmM/d [Nm /kg kg 1/m ] = [N] 0, dielectric constant Strong F.: (nuclear force) Acts within the nuclei of atoms: 8.854E-12 [C2/Nm2] [F/m] 2 2 2 2 2 F = 1/(40) (e /d ) [(CC/m )(Nm /C )] = [N] , 3.14 [-] Weak F.: Manifests itself in special reactions among elementary e, 1.60210 E-19 [As] [C] particles, such as the reaction that occur in radioactive decay.
    [Show full text]
  • EMT UNIT 1 (Laws of Reflection and Refraction, Total Internal Reflection).Pdf
    Electromagnetic Theory II (EMT II); Online Unit 1. REFLECTION AND TRANSMISSION AT OBLIQUE INCIDENCE (Laws of Reflection and Refraction and Total Internal Reflection) (Introduction to Electrodynamics Chap 9) Instructor: Shah Haidar Khan University of Peshawar. Suppose an incident wave makes an angle θI with the normal to the xy-plane at z=0 (in medium 1) as shown in Figure 1. Suppose the wave splits into parts partially reflecting back in medium 1 and partially transmitting into medium 2 making angles θR and θT, respectively, with the normal. Figure 1. To understand the phenomenon at the boundary at z=0, we should apply the appropriate boundary conditions as discussed in the earlier lectures. Let us first write the equations of the waves in terms of electric and magnetic fields depending upon the wave vector κ and the frequency ω. MEDIUM 1: Where EI and BI is the instantaneous magnitudes of the electric and magnetic vector, respectively, of the incident wave. Other symbols have their usual meanings. For the reflected wave, Similarly, MEDIUM 2: Where ET and BT are the electric and magnetic instantaneous vectors of the transmitted part in medium 2. BOUNDARY CONDITIONS (at z=0) As the free charge on the surface is zero, the perpendicular component of the displacement vector is continuous across the surface. (DIꓕ + DRꓕ ) (In Medium 1) = DTꓕ (In Medium 2) Where Ds represent the perpendicular components of the displacement vector in both the media. Converting D to E, we get, ε1 EIꓕ + ε1 ERꓕ = ε2 ETꓕ ε1 ꓕ +ε1 ꓕ= ε2 ꓕ Since the equation is valid for all x and y at z=0, and the coefficients of the exponentials are constants, only the exponentials will determine any change that is occurring.
    [Show full text]
  • Chapter 22 Reflection and Refraction of Light
    Chapter 22 Reflection and Refraction of Light Problem Solutions 22.1 The total distance the light travels is d2 Dcenter to R Earth R Moon center 2 3.84 108 6.38 10 6 1.76 10 6 m 7.52 10 8 m d 7.52 108 m Therefore, v 3.00 108 m s t 2.51 s 22.2 (a) The energy of a photon is sinc nair n prism 1.00 n prism , where Planck’ s constant is 1.00 8 sinc sin 45 and the speed of light in vacuum is c 3.00 10 m s . If nprism 1.00 1010 m , 6.63 1034 J s 3.00 10 8 m s E 1.99 1015 J 1.00 10-10 m 1 eV (b) E 1.99 1015 J 1.24 10 4 eV 1.602 10-19 J (c) and (d) For the X-rays to be more penetrating, the photons should be more energetic. Since the energy of a photon is directly proportional to the frequency and inversely proportional to the wavelength, the wavelength should decrease , which is the same as saying the frequency should increase . 1 eV 22.3 (a) E hf 6.63 1034 J s 5.00 10 17 Hz 2.07 10 3 eV 1.60 1019 J 355 356 CHAPTER 22 34 8 hc 6.63 10 J s 3.00 10 m s 1 nm (b) E hf 6.63 1019 J 3.00 1029 nm 10 m 1 eV E 6.63 1019 J 4.14 eV 1.60 1019 J c 3.00 108 m s 22.4 (a) 5.50 107 m 0 f 5.45 1014 Hz (b) From Table 22.1 the index of refraction for benzene is n 1.501.
    [Show full text]
  • 9.2 Refraction and Total Internal Reflection
    9.2 refraction and total internal reflection When a light wave strikes a transparent material such as glass or water, some of the light is reflected from the surface (as described in Section 9.1). The rest of the light passes through (transmits) the material. Figure 1 shows a ray that has entered a glass block that has two parallel sides. The part of the original ray that travels into the glass is called the refracted ray, and the part of the original ray that is reflected is called the reflected ray. normal incident ray reflected ray ␪ ␪i r ␪r ϭ ␪i air glass ␪2 refracted ray Figure 1 A light ray that strikes a glass surface is both reflected and refracted. Refracted and reflected rays of light account for many things that we encounter in our everyday lives. For example, the water in a pool can look shallower than it really is. A stick can look as if it bends at the point where it enters the water. On a hot day, the road ahead can appear to have a puddle of water, which turns out to be a mirage. These effects are all caused by the refraction and reflection of light. refraction The direction of the refracted ray is different from the direction of the incident refraction the bending of light as it ray, an effect called refraction. As with reflection, you can measure the direction of travels at an angle from one medium the refracted ray using the angle that it makes with the normal. In Figure 1, this to another angle is labelled θ2.
    [Show full text]
  • Descartes' Optics
    Descartes’ Optics Jeffrey K. McDonough Descartes’ work on optics spanned his entire career and represents a fascinating area of inquiry. His interest in the study of light is already on display in an intriguing study of refraction from his early notebook, known as the Cogitationes privatae, dating from 1619 to 1621 (AT X 242-3). Optics figures centrally in Descartes’ The World, or Treatise on Light, written between 1629 and 1633, as well as, of course, in his Dioptrics published in 1637. It also, however, plays important roles in the three essays published together with the Dioptrics, namely, the Discourse on Method, the Geometry, and the Meteorology, and many of Descartes’ conclusions concerning light from these earlier works persist with little substantive modification into the Principles of Philosophy published in 1644. In what follows, we will look in a brief and general way at Descartes’ understanding of light, his derivations of the two central laws of geometrical optics, and a sampling of the optical phenomena he sought to explain. We will conclude by noting a few of the many ways in which Descartes’ efforts in optics prompted – both through agreement and dissent – further developments in the history of optics. Descartes was a famously systematic philosopher and his thinking about optics is deeply enmeshed with his more general mechanistic physics and cosmology. In the sixth chapter of The Treatise on Light, he asks his readers to imagine a new world “very easy to know, but nevertheless similar to ours” consisting of an indefinite space filled everywhere with “real, perfectly solid” matter, divisible “into as many parts and shapes as we can imagine” (AT XI ix; G 21, fn 40) (AT XI 33-34; G 22-23).
    [Show full text]
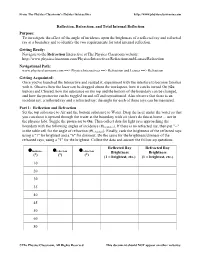
  • Reflection, Refraction, and Total Internal Reflection
    From The Physics Classroom's Physics Interactives http://www.physicsclassroom.com Reflection, Refraction, and Total Internal Reflection Purpose: To investigate the effect of the angle of incidence upon the brightness of a reflected ray and refracted ray at a boundary and to identify the two requirements for total internal reflection. Getting Ready: Navigate to the Refraction Interactive at The Physics Classroom website: http://www.physicsclassroom.com/Physics-Interactives/Refraction-and-Lenses/Refraction Navigational Path: www.physicsclassroom.com ==> Physics Interactives ==> Refraction and Lenses ==> Refraction Getting Acquainted: Once you've launched the Interactive and resized it, experiment with the interface to become familiar with it. Observe how the laser can be dragged about the workspace, how it can be turned On (Go button) and Cleared, how the substance on the top and the bottom of the boundary can be changed, and how the protractor can be toggled on and off and repositioned. Also observe that there is an incident ray, a reflected ray and a refracted ray; the angle for each of these rays can be measured. Part 1: Reflection and Refraction Set the top substance to Air and the bottom substance to Water. Drag the laser under the water so that you can shoot it upward through the water at the boundary with air (don't do this at home ... nor in the physics lab). Toggle the protractor to On. Then collect data for light rays approaching the boundary with the following angles of incidence (Θincidence). If there is no refracted ray, then put "--" in the table cell for the angle of refraction (Θrefraction).
    [Show full text]
  • Physics 30 Lesson 8 Refraction of Light
    Physics 30 Lesson 8 Refraction of Light Refer to Pearson pages 666 to 674. I. Reflection and refraction of light At any interface between two different mediums, some light will be reflected and some will be refracted, except in certain cases which we will soon discover. When problem solving for refraction, we usually ignore the reflected ray. Glass prism II. Index of refraction The fastest that light can travel is in a vacuum (c = 3.00 x 108 m/s). In other substances, the speed of light is always slower. The index of refraction is a ratio of the speed of light in vacuum with the speed of light in the medium: speed in vacuum (c) index of refraction (n) speed in medium (v) c n= v Some common indices of refraction are: Substance Index of refraction (n) vacuum 1.0000 Notice that the index of refraction (n) air 1.0003 is always greater than or equal to 1 water 1.33 ethyl alcohol 1.36 and that it has no units. quartz (fused) 1.46 glycerine 1.47 Lucite or Plexiglas 1.51 glass (crown) 1.52 sodium chloride 1.53 glass (crystal) 1.54 ruby 1.54 glass (flint) 1.65 zircon 1.92 diamond 2.42 Dr. Ron Licht 8 – 1 www.structuredindependentlearning.com Example 1 The index of refraction for crown glass was measured to be 1.52. What is the speed of light in crown glass? c n v c v n 3.00 108 m v s 1.52 8 m v 1.97 ×10 s III.
    [Show full text]
  • Chapter 22 Reflection and Refraction of Light Wavelength the Distance Between Any Two Crests of the Wave Is Defined As the Wavel
    Chapter 22 Reflection and Refraction of Light Wavelength Dual Nature of Light The distance between any two crests of the • Experiments can be devised that will wave is defined as the wavelength display either the wave nature or the particle nature of light • Nature prevents testing both qualities at the same time Geometric Optics – Using a Ray The Nature of Light Approximation • “Particles” of light are called photons • Light travels in a straight-line path in a • Each photon has a particular energy homogeneous medium until it –E = h ƒ encounters a boundary between two – h is Planck’s constant different media • h = 6.63 x 10-34 J s •The ray approximation is used to – Encompasses both natures of light represent beams of light • Interacts like a particle •A ray of light is an imaginary line drawn • Has a given frequency like a wave along the direction of travel of the light beams Ray Approximation Geometric Optics •A wave front is a surface passing through points of a wave that have the same phase and amplitude • The rays, corresponding to the direction of the wave motion, are perpendicular to the wave fronts Reflection QUICK QUIZ 22.1 Diffuse refection: The objects has irregularities that spread out an initially parallel beam of Which part of the figure below shows specular reflection of light in all directions to produce light from the roadway? diffuse reflection Specular reflection (mirror): When a parallel beam of light is directed at a smooth surface, it is specularly reflected in only one direction. The color of an object we see depends on two things: Law of Reflection The angle of incidence = the angle of reflection The kind of light falling on it and nature of its surface For instance, if white light is used to illuminate an object that absorbs all color other than red, the object will appear red.
    [Show full text]
  • Light Refraction with Dispersion Steven Cropp & Eric Zhang
    Light Refraction with Dispersion Steven Cropp & Eric Zhang 1. Abstract In this paper we present ray tracing and photon mapping methods to model light refraction, caustics, and multi colored light dispersion. We cover the solution to multiple common implementation difficulties, and mention ways to extend implementations in the future. 2. Introduction Refraction is when light rays bend at the boundaries of two different mediums. The amount light bends depends on the change in the speed of the light between the two mediums, which itself is dependent on a property of the materials. Every material has an index of refraction, a dimensionless number that describes how light (or any radiation) travels through that material. For example, water has an index of refraction of 1.33, which means light travels 33 percent slower in water than in a vacuum (which has the defining index of refraction of 1). Refraction is described by Snell’s Law, which calculates the new direction of the light ray based on the ray’s initial direction, as well as the two mediums it is exiting and entering. Chromatic dispersion occurs when a material’s index of refraction is not a constant, but a function of the wavelength of light. This causes different wavelengths, or colors, to refract at slightly different angles even when crossing the same material border. This slight variation splits the light into bands based on wavelength, creating a rainbow. This phenomena can be recreated by using a Cauchy approximation of an object’s index of refraction. 3. Related Work A “composite spectral model” was proposed by Sun et al.
    [Show full text]
  • 8 Reflection and Refraction
    Physics 212 Lab Lab 8 Reflection and Refraction What You Need To Know: The Physics Now that you have completed all of the labs dealing with circuits, you will move on to the next area of physics, light and optics. In this lab you will be exploring the first part of optics, the reflection and refraction of light at a plane (flat) surface and a curved surface. NORMAL INCIDENT RAY REFLECTED RAY I R MIRROR FIGURE 1 - Reflection off of a mirror Reflection occurs when an incident ray of light bounces off of a smooth flat surface like a mirror. See Figure 1. Refraction occurs when a ray of light that is traveling in one medium, let’s say air, enters a different medium, let’s say glass, and changes the direction of its path. See Figure 2. In order to describe reflection or refraction at a plane surface you need to measure angles with respect to a common reference line. The reference line that is used is called a normal. A normal is a line that is perpendicular to a surface. In Figure 1 you see a ray of light that is incident on a plane surface. The angle of incidence, I, of a ray of light is defined as the angle between the incident ray and the normal. If the surface is a mirror, then the angle of reflection, R, of a ray of light is defined as the angle between the reflected ray and the normal. In order to describe reflection or refraction at a plane surface you need to measure angles with respect to a common reference line.
    [Show full text]
  • Refractive Index and Dispersion of Liquid Hydrogen
    &1 Bureau of Standards .ifcrary, M.W. Bldg OCT 11 B65 ^ecknlcciL ^iote 9?©. 323 REFRACTIVE INDEX AND DISPERSION OF LIQUID HYDROGEN R. J. CORRUCCINI U. S. DEPARTMENT OF COMMERCE NATIONAL BUREAU OF STANDARDS THE NATIONAL BUREAU OF STANDARDS The National Bureau of Standards is a principal focal point in the Federal Government for assuring maximum application of the physical and engineering sciences to the advancement of technology in industry and commerce. Its responsibilities include development and maintenance of the national stand- ards of measurement, and the provisions of means for making measurements consistent with those standards; determination of physical constants and properties of materials; development of methods for testing materials, mechanisms, and structures, and making such tests as may be necessary, particu- larly for government agencies; cooperation in the establishment of standard practices for incorpora- tion in codes and specifications; advisory service to government agencies on scientific and technical problems; invention and development of devices to serve special needs of the Government; assistance to industry, business, and consumers in the development and acceptance of commercial standards and simplified trade practice recommendations; administration of programs in cooperation with United States business groups and standards organizations for the development of international standards of practice; and maintenance of a clearinghouse for the collection and dissemination of scientific, tech- nical, and engineering information. The scope of the Bureau's activities is suggested in the following listing of its four Institutes and their organizational units. Institute for Basic Standards. Applied Mathematics. Electricity. Metrology. Mechanics. Heat. Atomic Physics. Physical Chemistry. Laboratory Astrophysics.* Radiation Physics. Radio Standards Laboratory:* Radio Standards Physics; Radio Standards Engineering.
    [Show full text]
  • Reflections and Refractions in Ray Tracing
    Reflections and Refractions in Ray Tracing Bram de Greve ([email protected]) November 13, 2006 Abstract materials could be air (η ≈ 1), water (20◦C: η ≈ 1.33), glass (crown glass: η ≈ 1.5), ... It does not matter which refractive index is the greatest. All that counts is that η is the refractive When writing a ray tracer, sooner or later you’ll stumble 1 index of the material you come from, and η of the material on the problem of reflection and transmission. To visualize 2 you go to. This (very important) concept is sometimes misun- mirror-like objects, you need to reflect your viewing rays. To derstood. simulate a lens, you need refraction. While most people have heard of the law of reflection and Snell’s law, they often have The direction vector of the incident ray (= incoming ray) is i, difficulties with actually calculating the direction vectors of and we assume this vector is normalized. The direction vec- the reflected and refracted rays. In the following pages, ex- tors of the reflected and transmitted rays are r and t and will actly this problem will be addressed. As a bonus, some Fres- be calculated. These vectors are (or will be) normalized as nel equations will be added to the mix, so you can actually well. We also have the normal vector n, orthogonal to the in- calculate how much light is reflected or transmitted (yes, it’s terface and pointing towards the first material η1. Again, n is possible). At the end, you’ll have some usable formulas to use normalized.
    [Show full text]