DOCSLIB.ORG

A Non-Hohmann Method for Orbital Element Database Pre-Processing

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Non-Hohmann Method for Orbital Element Database Pre-Processing SSC20-WKI-09 A Non-Hohmann Method for Orbital Element Database Pre-Processing William O. S. Hudnut, Cameron P. Mehlman, Kurt S. Anderson Department of Mechanical, Aerospace, and Nuclear Engineering Rensselaer Polytechnic Institute JEC 2049 Jonsson Engineering Center 110 8th Street Troy, NY 12180 USA 802-356-0329 [email protected] May 2020 ABSTRACT One major obstacle to successful orbital debris remediation is the determination of which pieces of debris are the most viable targets for capture and de-orbit. The viability of a target is deter- mined by some combination of the debris’ risk factor (a combination of its size, composition, and the orbit it occupies), the anticipated resource cost to find and capture the debris, and the un- derlying probability of successful intercept and capture of that target. The problem of selecting debris for capture by a multi-capture capable spacecraft is fundamentally a traveling salesman problem in which the traveler only has the resources to reach a very limited subset of the available destinations. Therefore, rapidly identifying the sets of destinations (i.e. pieces of debris) which are either too expensive to reach or insufficiently valuable to justify targeting will reduce the tar- get destination set; this would significantly enhance the efficiency of the solution. This problem of intelligently reducing the space of possible solutions can be partially solved by performing a preliminary filtering and sorting of orbital debris database entries using known spacecraft or- bital parameters and maneuvering ∆V-budget to reduce the number of possible destinations for an optimizer to those which are in fact accessible from the spacecraft’s initial orbit. The chosen algorithm for analyzing and filtering the data is a two-burn node-to-node non-Hohmann transfer, which was used to estimate the ∆V-cost for transfer from the capture spacecraft’s initial orbit to an orbit near the target piece of debris. Once the ∆V-cost was calculated for each transfer orbit, entries with excessive fuel costs were removed from consideration, and the fuel cost to access each remaining orbit was appended to its entry. This method was capable of reducing a 10,400- item list of debris to less than 100 accessible targets in under 3 seconds on an ordinary laptop computer. This reduction in database size brought the number of targets down to a practical size for processing by a more computationally expensive optimization algorithm suitable for selecting final targets for a multi-capture spacecraft. Hudnut1 34th Annual Small Satellite Conference INTRODUCTION (each OSCaR is equipped with only 3 to 4 nets depending on the CubeSat configuration). The In 1958, the United States’ Vanguard I satel- ephemeris data of cataloged pieces of debris in lite became the first man-made object to en- orbit around the earth is recorded by organiza- ter orbit around earth without reentering the tions such as NORAD, and can be obtained in atmosphere. Since then, due to the increase the form of two-line elements [10]. To facilitate of man made objects in orbit as well as satel- the greatest probability of success of the mis- lite collisions, the amount of detritus in orbit sion, this list must be reduced to those pieces around earth has increased exponentially. The of debris that require acceptable quantities of ESA estimates over 100 million pieces of debris propellant to find, capture, and deorbit given orbit Earth at every moment, most are smaller an OSCaR’s initial orbit. The first step in nar- than 10 cm [7]. Debris of this size creates huge rowing this list to the final target set is to use risks for any space endeavor within Earth’s an algorithm that can remove pieces of debris orbit because they are difficult to avoid and that cannot be obtained without exceeding a travel at hypersonic speeds (up to 7.8 km/s). given ∆V budget. A collision at these speeds can cause severe damage to a spacecraft; even flecks of paint The purpose of this algorithm is to conduct a have been known to crater and crack windows. preliminary search, such that the reduced list The most imminent threat from space debris is is of a manageable size for a more accurate and that with increasing numbers of debris in orbit, computationally expensive optimizer that will there is an increasing chance of debris perpet- determine the final targets. The sorter esti- ually colliding and breaking down into smaller mates the amount of fuel required to complete pieces. As a result, vast regions of low-earth or- a two-burn node-to-node non-Hohmann trans- bit (LEO) space could be deemed unusable due fer from the satellite’s orbit to the debris’ orbit. to fields of small yet highly dangerous parti- Debris that required more ∆V than the prede- cles. This hypothesized cascading of collisions termined limit are removed from the list. The yielding an exponential growth in the number algorithm described herein does not currently of pieces of fragmented debris is also known as consider additional propellant required for any Kessler’s Syndrome [20]. phasing burns required to realize the subse- quent OSCaR-debris rendezvous once OSCaR In the past, there has been little to no effort has placed itself in the debris piece orbit. The to actively reduce the amount of debris in or- sorter returns a final sorted list of all debris bit around Earth, and most proposals only tar- within an optimal ∆V range of the satellite. get larger intact spacecraft. OSCaR (Obsolete Spacecraft Capture and Removal) is a 3-unit METHOD CubeSat satellite system designed to target, capture, and de-orbit smaller debris in LEO The overall goal of the sorter program was (of approximately 1 to 20 cm in size). OSCaR to produce a reduced list of accessible ren- is being developed to pursue individual pieces dezvous targets from a database file of debris of debris and then, capture its target using targets, an initial set of orbital parameters for a weighted net. The debris and net is slowly the spacecraft, and an onboard fuel budget for pulled into the atmosphere, through the use the spacecraft. In order to achieve this goal, of electromagnetic tethers [19], where they will four steps needed to be undertaken. First, burn up upon re-entry. The final piece of de- a suitable target set had to be obtained from bris captured by OSCaR is deorbited along with existing databases. Second, the data thus the spacecraft as OSCaR uses its remaining obtained needed to be manipulated in order fuel reserve to place itself into an eliptical orbit to produce classical orbital parameters in a which dips into the atmosphere and decays. convenient format for large-scale processing. Third, an algorithmic method of calculating the OSCaR’s target set is received from a grounded delta-V required to reach a target orbit needed station where thousands of known pieces of to be implemented. Finally, the data set needed debris are taken into consideration, evaluated to be cleared of impractical targets and pro- and the final debris target set is selected. Be- vided in a convenient format for later process- cause of the size of CubeSat satellites, OSCaR ing. has both substantial limits on fuel and nets Hudnut2 34th Annual Small Satellite Conference Orbital ephemeris data can be retrieved from transfer orbit is usually optimal for co-planar several sources, including the European Space initial and final orbits, in the case of orbital de- Agency [7] and Space-Track.org [16]. These bris rendezvous it is likely that the debris will databases usually store the ephemeris data for be out-of-plane with respect to the initial orbit observed satellites and debris in the two-line of the spacecraft, and will have randomly ori- element (TLE) format. In order to achieve the ented apse lines. first step of the process, the acquisition of or- bital data for debris, the team turned to a M.S. In most cases for a non-Hohmann orbital thesis by Philip Hoddinott associated with the transfer, time-optimal transfers are preferred. OSCaR project. This thesis was on the devel- These transfer maneuvers are usually calcu- opment of a method for retrieving open-source lated by a method which iteratively solves Lam- orbital data in a program usable by anyone fa- bert’s problem [18]. However, while these so- miliar with basic orbital mechanics and MAT- lutions are good for exact intercepts between LAB coding [10]. This program scanned the spacecraft, they are computationally intensive Space-Track.org TLE database for orbiting bod- due to their iterative nature [5]. Therefore, an ies categorized as "debris" appearing after a analytical method of trajectory and ∆V calcula- given date, and then generated a MATLAB data tion was derived in order to save computational file and populated it with the TLE data thus re- time for the purposes of the initial filtering al- trieved. gorithm. Wrapper The following derivation is a method to cal- culate the ∆V required for a two-burn non- The second and fourth steps of the process are Hohmann transfer between two inclined ellip- handled in the wrapper script, which intakes tical orbits, called orbits 1 and 2, where these the TLE data file, processes it into a useful orbits have arbitrarily oriented apse lines. The format, passes it to the calculation algorithm, departure burn occurs at a point on the line and then cleans the resultant data of target or- of nodes on the initial orbit, and the insertion bits which the spacecraft cannot reach. It also burn occurs at a point on the line of nodes on contains the user-input orbital parameters and the other orbit, nominally the final orbit, op- ∆V budget of the OSCaR spacecraft.
Load more

Recommended publications
  • The Utilization of Halo Orbit§ in Advanced Lunar Operation§
    NASA TECHNICAL NOTE NASA TN 0-6365 VI *o M *o d a THE UTILIZATION OF HALO ORBIT§ IN ADVANCED LUNAR OPERATION§ by Robert W. Fmqcbar Godddrd Spctce Flight Center P Greenbelt, Md. 20771 NATIONAL AERONAUTICS AND SPACE ADMINISTRATION WASHINGTON, D. C. JULY 1971 1. Report No. 2. Government Accession No. 3. Recipient's Catalog No. NASA TN D-6365 5. Report Date Jul;v 1971. 6. Performing Organization Code 8. Performing Organization Report No, G-1025 10. Work Unit No. Goddard Space Flight Center 11. Contract or Grant No. Greenbelt, Maryland 20 771 13. Type of Report and Period Covered 2. Sponsoring Agency Name and Address Technical Note J National Aeronautics and Space Administration Washington, D. C. 20546 14. Sponsoring Agency Code 5. Supplementary Notes 6. Abstract Flight mechanics and control problems associated with the stationing of space- craft in halo orbits about the translunar libration point are discussed in some detail. Practical procedures for the implementation of the control techniques are described, and it is shown that these procedures can be carried out with very small AV costs. The possibility of using a relay satellite in.a halo orbit to obtain a continuous com- munications link between the earth and the far side of the moon is also discussed. Several advantages of this type of lunar far-side data link over more conventional relay-satellite systems are cited. It is shown that, with a halo relay satellite, it would be possible to continuously control an unmanned lunar roving vehicle on the moon's far side. Backside tracking of lunar orbiters could also be realized.
    [Show full text]
  • AAS 13-250 Hohmann Spiral Transfer with Inclination Change Performed
    AAS 13-250 Hohmann Spiral Transfer With Inclination Change Performed By Low-Thrust System Steven Owens1 and Malcolm Macdonald2 This paper investigates the Hohmann Spiral Transfer (HST), an orbit transfer method previously developed by the authors incorporating both high and low- thrust propulsion systems, using the low-thrust system to perform an inclination change as well as orbit transfer. The HST is similar to the bi-elliptic transfer as the high-thrust system is first used to propel the spacecraft beyond the target where it is used again to circularize at an intermediate orbit. The low-thrust system is then activated and, while maintaining this orbit altitude, used to change the orbit inclination to suit the mission specification. The low-thrust system is then used again to reduce the spacecraft altitude by spiraling in-toward the target orbit. An analytical analysis of the HST utilizing the low-thrust system for the inclination change is performed which allows a critical specific impulse ratio to be derived determining the point at which the HST consumes the same amount of fuel as the Hohmann transfer. A critical ratio is found for both a circular and elliptical initial orbit. These equations are validated by a numerical approach before being compared to the HST utilizing the high-thrust system to perform the inclination change. An additional critical ratio comparing the HST utilizing the low-thrust system for the inclination change with its high-thrust counterpart is derived and by using these three critical ratios together, it can be determined when each transfer offers the lowest fuel mass consumption.
    [Show full text]
  • Low-Energy Lunar Trajectory Design
    LOW-ENERGY LUNAR TRAJECTORY DESIGN Jeffrey S. Parker and Rodney L. Anderson Jet Propulsion Laboratory Pasadena, California July 2013 ii DEEP SPACE COMMUNICATIONS AND NAVIGATION SERIES Issued by the Deep Space Communications and Navigation Systems Center of Excellence Jet Propulsion Laboratory California Institute of Technology Joseph H. Yuen, Editor-in-Chief Published Titles in this Series Radiometric Tracking Techniques for Deep-Space Navigation Catherine L. Thornton and James S. Border Formulation for Observed and Computed Values of Deep Space Network Data Types for Navigation Theodore D. Moyer Bandwidth-Efficient Digital Modulation with Application to Deep-Space Communication Marvin K. Simon Large Antennas of the Deep Space Network William A. Imbriale Antenna Arraying Techniques in the Deep Space Network David H. Rogstad, Alexander Mileant, and Timothy T. Pham Radio Occultations Using Earth Satellites: A Wave Theory Treatment William G. Melbourne Deep Space Optical Communications Hamid Hemmati, Editor Spaceborne Antennas for Planetary Exploration William A. Imbriale, Editor Autonomous Software-Defined Radio Receivers for Deep Space Applications Jon Hamkins and Marvin K. Simon, Editors Low-Noise Systems in the Deep Space Network Macgregor S. Reid, Editor Coupled-Oscillator Based Active-Array Antennas Ronald J. Pogorzelski and Apostolos Georgiadis Low-Energy Lunar Trajectory Design Jeffrey S. Parker and Rodney L. Anderson LOW-ENERGY LUNAR TRAJECTORY DESIGN Jeffrey S. Parker and Rodney L. Anderson Jet Propulsion Laboratory Pasadena, California July 2013 iv Low-Energy Lunar Trajectory Design July 2013 Jeffrey Parker: I dedicate the majority of this book to my wife Jen, my best friend and greatest support throughout the development of this book and always.
    [Show full text]
  • Analysis of Perturbations and Station-Keeping Requirements in Highly-Inclined Geosynchronous Orbits
    ANALYSIS OF PERTURBATIONS AND STATION-KEEPING REQUIREMENTS IN HIGHLY-INCLINED GEOSYNCHRONOUS ORBITS Elena Fantino(1), Roberto Flores(2), Alessio Di Salvo(3), and Marilena Di Carlo(4) (1)Space Studies Institute of Catalonia (IEEC), Polytechnic University of Catalonia (UPC), E.T.S.E.I.A.T., Colom 11, 08222 Terrassa (Spain), [email protected] (2)International Center for Numerical Methods in Engineering (CIMNE), Polytechnic University of Catalonia (UPC), Building C1, Campus Norte, UPC, Gran Capitan,´ s/n, 08034 Barcelona (Spain) (3)NEXT Ingegneria dei Sistemi S.p.A., Space Innovation System Unit, Via A. Noale 345/b, 00155 Roma (Italy), [email protected] (4)Department of Mechanical and Aerospace Engineering, University of Strathclyde, 75 Montrose Street, Glasgow G1 1XJ (United Kingdom), [email protected] Abstract: There is a demand for communications services at high latitudes that is not well served by conventional geostationary satellites. Alternatives using low-altitude orbits require too large constellations. Other options are the Molniya and Tundra families (critically-inclined, eccentric orbits with the apogee at high latitudes). In this work we have considered derivatives of the Tundra type with different inclinations and eccentricities. By means of a high-precision model of the terrestrial gravity field and the most relevant environmental perturbations, we have studied the evolution of these orbits during a period of two years. The effects of the different perturbations on the constellation ground track (which is more important for coverage than the orbital elements themselves) have been identified. We show that, in order to maintain the ground track unchanged, the most important parameters are the orbital period and the argument of the perigee.
    [Show full text]
  • Appendix a Orbits
    Appendix A Orbits As discussed in the Introduction, a good ¯rst approximation for satellite motion is obtained by assuming the spacecraft is a point mass or spherical body moving in the gravitational ¯eld of a spherical planet. This leads to the classical two-body problem. Since we use the term body to refer to a spacecraft of ¯nite size (as in rigid body), it may be more appropriate to call this the two-particle problem, but I will use the term two-body problem in its classical sense. The basic elements of orbital dynamics are captured in Kepler's three laws which he published in the 17th century. His laws were for the orbital motion of the planets about the Sun, but are also applicable to the motion of satellites about planets. The three laws are: 1. The orbit of each planet is an ellipse with the Sun at one focus. 2. The line joining the planet to the Sun sweeps out equal areas in equal times. 3. The square of the period of a planet is proportional to the cube of its mean distance to the sun. The ¯rst law applies to most spacecraft, but it is also possible for spacecraft to travel in parabolic and hyperbolic orbits, in which case the period is in¯nite and the 3rd law does not apply. However, the 2nd law applies to all two-body motion. Newton's 2nd law and his law of universal gravitation provide the tools for generalizing Kepler's laws to non-elliptical orbits, as well as for proving Kepler's laws.
    [Show full text]
  • Astrodynamics
    Politecnico di Torino SEEDS SpacE Exploration and Development Systems Astrodynamics II Edition 2006 - 07 - Ver. 2.0.1 Author: Guido Colasurdo Dipartimento di Energetica Teacher: Giulio Avanzini Dipartimento di Ingegneria Aeronautica e Spaziale e-mail: [email protected] Contents 1 Two–Body Orbital Mechanics 1 1.1 BirthofAstrodynamics: Kepler’sLaws. ......... 1 1.2 Newton’sLawsofMotion ............................ ... 2 1.3 Newton’s Law of Universal Gravitation . ......... 3 1.4 The n–BodyProblem ................................. 4 1.5 Equation of Motion in the Two-Body Problem . ....... 5 1.6 PotentialEnergy ................................. ... 6 1.7 ConstantsoftheMotion . .. .. .. .. .. .. .. .. .... 7 1.8 TrajectoryEquation .............................. .... 8 1.9 ConicSections ................................... 8 1.10 Relating Energy and Semi-major Axis . ........ 9 2 Two-Dimensional Analysis of Motion 11 2.1 ReferenceFrames................................. 11 2.2 Velocity and acceleration components . ......... 12 2.3 First-Order Scalar Equations of Motion . ......... 12 2.4 PerifocalReferenceFrame . ...... 13 2.5 FlightPathAngle ................................. 14 2.6 EllipticalOrbits................................ ..... 15 2.6.1 Geometry of an Elliptical Orbit . ..... 15 2.6.2 Period of an Elliptical Orbit . ..... 16 2.7 Time–of–Flight on the Elliptical Orbit . .......... 16 2.8 Extensiontohyperbolaandparabola. ........ 18 2.9 Circular and Escape Velocity, Hyperbolic Excess Speed . .............. 18 2.10 CosmicVelocities
    [Show full text]
  • A Hot Subdwarf-White Dwarf Super-Chandrasekhar Candidate
    A hot subdwarf–white dwarf super-Chandrasekhar candidate supernova Ia progenitor Ingrid Pelisoli1,2*, P. Neunteufel3, S. Geier1, T. Kupfer4,5, U. Heber6, A. Irrgang6, D. Schneider6, A. Bastian1, J. van Roestel7, V. Schaffenroth1, and B. N. Barlow8 1Institut fur¨ Physik und Astronomie, Universitat¨ Potsdam, Haus 28, Karl-Liebknecht-Str. 24/25, D-14476 Potsdam-Golm, Germany 2Department of Physics, University of Warwick, Coventry, CV4 7AL, UK 3Max Planck Institut fur¨ Astrophysik, Karl-Schwarzschild-Straße 1, 85748 Garching bei Munchen¨ 4Kavli Institute for Theoretical Physics, University of California, Santa Barbara, CA 93106, USA 5Texas Tech University, Department of Physics & Astronomy, Box 41051, 79409, Lubbock, TX, USA 6Dr. Karl Remeis-Observatory & ECAP, Astronomical Institute, Friedrich-Alexander University Erlangen-Nuremberg (FAU), Sternwartstr. 7, 96049 Bamberg, Germany 7Division of Physics, Mathematics and Astronomy, California Institute of Technology, Pasadena, CA 91125, USA 8Department of Physics and Astronomy, High Point University, High Point, NC 27268, USA *[email protected] ABSTRACT Supernova Ia are bright explosive events that can be used to estimate cosmological distances, allowing us to study the expansion of the Universe. They are understood to result from a thermonuclear detonation in a white dwarf that formed from the exhausted core of a star more massive than the Sun. However, the possible progenitor channels leading to an explosion are a long-standing debate, limiting the precision and accuracy of supernova Ia as distance indicators. Here we present HD 265435, a binary system with an orbital period of less than a hundred minutes, consisting of a white dwarf and a hot subdwarf — a stripped core-helium burning star.
    [Show full text]
  • Electric Propulsion System Scaling for Asteroid Capture-And-Return Missions
    Electric propulsion system scaling for asteroid capture-and-return missions Justin M. Little⇤ and Edgar Y. Choueiri† Electric Propulsion and Plasma Dynamics Laboratory, Princeton University, Princeton, NJ, 08544 The requirements for an electric propulsion system needed to maximize the return mass of asteroid capture-and-return (ACR) missions are investigated in detail. An analytical model is presented for the mission time and mass balance of an ACR mission based on the propellant requirements of each mission phase. Edelbaum’s approximation is used for the Earth-escape phase. The asteroid rendezvous and return phases of the mission are modeled as a low-thrust optimal control problem with a lunar assist. The numerical solution to this problem is used to derive scaling laws for the propellant requirements based on the maneuver time, asteroid orbit, and propulsion system parameters. Constraining the rendezvous and return phases by the synodic period of the target asteroid, a semi- empirical equation is obtained for the optimum specific impulse and power supply. It was found analytically that the optimum power supply is one such that the mass of the propulsion system and power supply are approximately equal to the total mass of propellant used during the entire mission. Finally, it is shown that ACR missions, in general, are optimized using propulsion systems capable of processing 100 kW – 1 MW of power with specific impulses in the range 5,000 – 10,000 s, and have the potential to return asteroids on the order of 103 104 tons. − Nomenclature
    [Show full text]
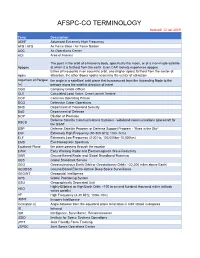
  • AFSPC-CO TERMINOLOGY Revised: 12 Jan 2019
    AFSPC-CO TERMINOLOGY Revised: 12 Jan 2019 Term Description AEHF Advanced Extremely High Frequency AFB / AFS Air Force Base / Air Force Station AOC Air Operations Center AOI Area of Interest The point in the orbit of a heavenly body, specifically the moon, or of a man-made satellite Apogee at which it is farthest from the earth. Even CAP rockets experience apogee. Either of two points in an eccentric orbit, one (higher apsis) farthest from the center of Apsis attraction, the other (lower apsis) nearest to the center of attraction Argument of Perigee the angle in a satellites' orbit plane that is measured from the Ascending Node to the (ω) perigee along the satellite direction of travel CGO Company Grade Officer CLV Calculated Load Value, Crew Launch Vehicle COP Common Operating Picture DCO Defensive Cyber Operations DHS Department of Homeland Security DoD Department of Defense DOP Dilution of Precision Defense Satellite Communications Systems - wideband communications spacecraft for DSCS the USAF DSP Defense Satellite Program or Defense Support Program - "Eyes in the Sky" EHF Extremely High Frequency (30-300 GHz; 1mm-1cm) ELF Extremely Low Frequency (3-30 Hz; 100,000km-10,000km) EMS Electromagnetic Spectrum Equitorial Plane the plane passing through the equator EWR Early Warning Radar and Electromagnetic Wave Resistivity GBR Ground-Based Radar and Global Broadband Roaming GBS Global Broadcast Service GEO Geosynchronous Earth Orbit or Geostationary Orbit ( ~22,300 miles above Earth) GEODSS Ground-Based Electro-Optical Deep Space Surveillance
    [Show full text]
  • Optimisation of Propellant Consumption for Power Limited Rockets
    Delft University of Technology Faculty Electrical Engineering, Mathematics and Computer Science Delft Institute of Applied Mathematics Optimisation of Propellant Consumption for Power Limited Rockets. What Role do Power Limited Rockets have in Future Spaceflight Missions? (Dutch title: Optimaliseren van brandstofverbruik voor vermogen gelimiteerde raketten. De rol van deze raketten in toekomstige ruimtevlucht missies. ) A thesis submitted to the Delft Institute of Applied Mathematics as part to obtain the degree of BACHELOR OF SCIENCE in APPLIED MATHEMATICS by NATHALIE OUDHOF Delft, the Netherlands December 2017 Copyright c 2017 by Nathalie Oudhof. All rights reserved. BSc thesis APPLIED MATHEMATICS \ Optimisation of Propellant Consumption for Power Limited Rockets What Role do Power Limite Rockets have in Future Spaceflight Missions?" (Dutch title: \Optimaliseren van brandstofverbruik voor vermogen gelimiteerde raketten De rol van deze raketten in toekomstige ruimtevlucht missies.)" NATHALIE OUDHOF Delft University of Technology Supervisor Dr. P.M. Visser Other members of the committee Dr.ir. W.G.M. Groenevelt Drs. E.M. van Elderen 21 December, 2017 Delft Abstract In this thesis we look at the most cost-effective trajectory for power limited rockets, i.e. the trajectory which costs the least amount of propellant. First some background information as well as the differences between thrust limited and power limited rockets will be discussed. Then the optimal trajectory for thrust limited rockets, the Hohmann Transfer Orbit, will be explained. Using Optimal Control Theory, the optimal trajectory for power limited rockets can be found. Three trajectories will be discussed: Low Earth Orbit to Geostationary Earth Orbit, Earth to Mars and Earth to Saturn. After this we compare the propellant use of the thrust limited rockets for these trajectories with the power limited rockets.
    [Show full text]
  • Use of MESSENGER Radioscience Data to Improve Planetary Ephemeris and to Test General Relativity
    A&A 561, A115 (2014) Astronomy DOI: 10.1051/0004-6361/201322124 & © ESO 2014 Astrophysics Use of MESSENGER radioscience data to improve planetary ephemeris and to test general relativity A. K. Verma1;2, A. Fienga3;4, J. Laskar4, H. Manche4, and M. Gastineau4 1 Observatoire de Besançon, UTINAM-CNRS UMR6213, 41bis avenue de l’Observatoire, 25000 Besançon, France e-mail: [email protected] 2 Centre National d’Études Spatiales, 18 avenue Édouard Belin, 31400 Toulouse, France 3 Observatoire de la Côte d’Azur, GéoAzur-CNRS UMR7329, 250 avenue Albert Einstein, 06560 Valbonne, France 4 Astronomie et Systèmes Dynamiques, IMCCE-CNRS UMR8028, 77 Av. Denfert-Rochereau, 75014 Paris, France Received 24 June 2013 / Accepted 7 November 2013 ABSTRACT The current knowledge of Mercury’s orbit has mainly been gained by direct radar ranging obtained from the 60s to 1998 and by five Mercury flybys made with Mariner 10 in the 70s, and with MESSENGER made in 2008 and 2009. On March 18, 2011, MESSENGER became the first spacecraft to orbit Mercury. The radioscience observations acquired during the orbital phase of MESSENGER drastically improved our knowledge of the orbit of Mercury. An accurate MESSENGER orbit is obtained by fitting one-and-half years of tracking data using GINS orbit determination software. The systematic error in the Earth-Mercury geometric positions, also called range bias, obtained from GINS are then used to fit the INPOP dynamical modeling of the planet motions. An improved ephemeris of the planets is then obtained, INPOP13a, and used to perform general relativity tests of the parametrized post-Newtonian (PPN) formalism.
    [Show full text]
  • Up, Up, and Away by James J
    www.astrosociety.org/uitc No. 34 - Spring 1996 © 1996, Astronomical Society of the Pacific, 390 Ashton Avenue, San Francisco, CA 94112. Up, Up, and Away by James J. Secosky, Bloomfield Central School and George Musser, Astronomical Society of the Pacific Want to take a tour of space? Then just flip around the channels on cable TV. Weather Channel forecasts, CNN newscasts, ESPN sportscasts: They all depend on satellites in Earth orbit. Or call your friends on Mauritius, Madagascar, or Maui: A satellite will relay your voice. Worried about the ozone hole over Antarctica or mass graves in Bosnia? Orbital outposts are keeping watch. The challenge these days is finding something that doesn't involve satellites in one way or other. And satellites are just one perk of the Space Age. Farther afield, robotic space probes have examined all the planets except Pluto, leading to a revolution in the Earth sciences -- from studies of plate tectonics to models of global warming -- now that scientists can compare our world to its planetary siblings. Over 300 people from 26 countries have gone into space, including the 24 astronauts who went on or near the Moon. Who knows how many will go in the next hundred years? In short, space travel has become a part of our lives. But what goes on behind the scenes? It turns out that satellites and spaceships depend on some of the most basic concepts of physics. So space travel isn't just fun to think about; it is a firm grounding in many of the principles that govern our world and our universe.
    [Show full text]