DOCSLIB.ORG

4.2 Stellar Evolution After the Giant Branch

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text

Load more

I*M*P*R*S on ASTROPHYSICS at LMU Munich Astrophysics Introductory Course Lecture given by: Ralf Bender and Roberto Saglia in collaboration with: Chris Botzler, Andre Crusius-Wätzel, Niv Drory, Georg Feulner, Armin Gabasch, Ulrich Hopp, Claudia Maraston, Michael Matthias, Jan Snigula, Daniel Thomas Powerpoint version with the help of Hanna Kotarba Fall 2007 IMPRS Astrophysics Introductory Course Fall 2007 1 Chapter 4 Stellar Evolution IMPRS Astrophysics Introductory Course Fall 2007 2 4.1 Stellar evolution from the main sequence to the giant branch Immediately after the contraction phase during stellar formation (before nuclear burning sets in) stars have a homogeneous chemical composition. The location of the stars in the HRD where they for the first time start with nuclear fusion in hydrostatic equilibrium is called Zero Age Main Sequence (ZAMS) For the period of central hydrogen burning the stars remain on the main sequence near the ZAMS. As the chemical composition changes slowly, the main sequence is not a line but a strip. Massive metal rich stars (M > 20MΘ) in addition loose a significant fraction of their mass due to stellar winds, which moves them a large distance away from the ZAMS even during the hydrogen burning phase. (Lower mass stars also develop winds but only in the later phases of their evolution.) How does a star move ’inside’ the main sequence? As shown above we have: IMPRS Astrophysics Introductory Course Fall 2007 3 Evolutionary paths in the HRD up to the point where He burning sets in (from Iben 1967, ARAA 5). The shade of the line segments indicates the time spent in the corresponding phases. MS (1-3) life-times: 1.0·MΘ: 9.0E9 yrs 2.2·MΘ: 5.0E8 yrs 15·MΘ: 1E7 yrs GB (5-6) life-times: 1.0·MΘ: 1.0E9 yrs 2.2·MΘ: 3.8E7 yrs 15·MΘ: 1.5E6 yrs (6-10) IMPRS Astrophysics Introductory Course Fall 2007 4 Hydrogen fusion leads to: Therefore, following our simple model, the luminosity and the temperatures during hydrogen burning should rise for both pp–chain and CNO–cycle. In reality temperature rises for the pp-chain while it decreases for the CNO-chain (where the core is convective and not radiative as assumed in the model). Once almost all of the core hydrogen is used up, hydrogen shell burning in a thick shell around the (He-) core starts. The star moves to cooler temperatures to the sub–giant branch with approximately constant luminosity. For M > 1.4MΘ the core is convective and XH so small that contraction has to set in before hydrogen shell burning can start. The hydrogen burning shell moves outward with time, whereas the helium core slowly contracts and increases its binding energy. The released gravitational energy heats the hydrogen burning shell from below, which increases the fusion (ε ~ T5..17) and forces the star out of equilibrium: The situation is analogous to the scale height of a planetary atmosphere H = kT/µmpg which is dependent on the temperature. The star expands and its temperature decreases as the energy transport is too inefficient to keep Teff constant. IMPRS Astrophysics Introductory Course Fall 2007 5 IMPRS Astrophysics Introductory Course Fall 2007 6 IMPRS Astrophysics Introductory Course Fall 2007 7 At the Hayashi–limit the star gets fully convective and the smallest possible temperature is reached. On the way from the main sequence to the Hayashi–limit the luminosity of the 4 2 −1/2 star changes only slightly: L ~ const. ~ Teff · R → Teff ~ R , i.e. R ↑ → Teff ↓. The transition from the main sequence to the Hayashi–limit is determined by the Kelvin– Helmholtz time scale (≈ 107 years — short!). The most massive stars now remain at the Hayashi–limit with constant luminosity. With the onset of helium burning they increase the temperature and move again to the left in the HRD. Less massive stars keep increasing their radius at approximate constant temperature thus increasing their luminosity ~ R2, they move upwards along the Hayashi line (→ giant branch stars!). The sun for example will expand up to the radius of the earth: Teff ≈ 3500 K, L ≈ 300 LΘ. IMPRS Astrophysics Introductory Course Fall 2007 8 Evolutionary paths in the HRD up to the point where He burning sets in (from Iben 1967, ARAA 5). The shade of the line segments indicates the time spent in the corresponding phases. MS (1-3) life-times: 1.0·MΘ: 9.0E9 yrs 2.2·MΘ: 5.0E8 yrs 15·MΘ: 1E7 yrs GB (5-6) life-times: 1.0·MΘ: 1.0E9 yrs 2.2·MΘ: 3.8E7 yrs 15·MΘ: 1.5E6 yrs (6-10) IMPRS Astrophysics Introductory Course Fall 2007 9 4.2 Stellar evolution after the giant branch The post giant branch evolution is dependent on the mass: M ≤ 0.5MΘ The pressure of the degenerated electron gas stops the contraction of the helium core 8 before Tc ≈ 10 K is reached. → no helium burning. H shell burning slowly stops, the star cools out. 0.5MΘ ≤ M ≤ 2.5MΘ The H shell burning puts more and more He onto the core, which keeps contracting. The core is supported by the pressure of the degenerate electron gas, while the pressure from the He nuclei is negligible. When the temperature has reached ~ 108 K, He–burning 30 suddenly starts (because of ε3α ~ Tc ). Because the pressure from the He nuclei is still negligible relative to the pressure of the degenerate electrons, the nuclear burning can 30 not be moderated via expansion. Again, because of ε3α ~ Tc , the energy production increases dramatically and a large fraction of the He is burned into C and O. → thermonuclear runaway! Only once the temperature of the nuclei is high enough to contribute significantly to the pressure, the core expands and the reaction is slowed down. The star expands on a hydrostatic time scale and reaches its highest luminosity at the tip of the giant branch: IMPRS Astrophysics Introductory Course Fall 2007 10 Helium flash Note: As helium burning sets in at the same core mass, all mass poor stars have the same luminosity at the tip of the giant branch. IMPRS Astrophysics Introductory Course Fall 2007 11 After the helium flash, the star is on the horizontal branch. The position on the horizontal branch depends on mass and metallicity. On the horizontal branch we have He → C burning in the core and H → He burning in a shell. In addition we have the following reactions: 12C + 4He → 16O + γ + 7.161 MeV 16O + 4He → 20Ne + γ + 4.730 MeV The result is a mixture of C and O (≈ 50 : 50) in the stars center. C/O sinks down to the core and replaces He which is driven out of the core. If the He is driven out of the core, helium burning shifts to shell burning. → same procedure as with hydrogen burning. The star expands again to the Hayashi line and then moves to higher luminosities along the asymptotic giant branch (AGB). IMPRS Astrophysics Introductory Course Fall 2007 12 Evolution of low mass stars with 0.7 and 0.8 solar masses. Times up to the giant branch are in billion years. From Iben 1971, in Boehm-Vitense: Stellar Astrophsics. IMPRS Astrophysics Introductory Course Fall 2007 13 Massive stars with M > 2.5MΘ Mostly the same evolution as for less massive stars. But, before ignition of helium burning the electron gas is not degenerated, thus we have a continous transition to helium burning. The star performs loops in the HRD at nearly constant luminosity. Evolution of a 5 solar mass star (Kippenhahn/Weigert). IMPRS Astrophysics Introductory Course Fall 2007 14 IMPRS Astrophysics Introductory Course Fall 2007 15 An important test for the theory of stellar structure and evolution is the analysis of HRD’s and color–luminosity–diagrams of open star clusters and globular clusters. These represent groups of stars of similar age and chemical composition but different mass and, therefore, the number of stars in the different parts of the HRD can directly be compared with the predictions of the theory. (diagram from Maeder et al., stars from galactic clusters) IMPRS Astrophysics Introductory Course Fall 2007 16 MS = main sequence TO = turn-off RGB = red giant branch HB = horizontal branch AGB = asymptotic giant b. P-AGB = post-AGB BS = blue stragglers IMPRS Astrophysics Introductory Course Fall 2007 17 IMPRS Astrophysics Introductory Course Fall 2007 18 4.3 Special effects 4.3.1 The Eddington luminosity The Eddington luminosity is the maximum luminosity a object of given mass can emit. At higher luminosities, radiation pressure wins over gravitational acceleration. The Eddington luminosity is an upper limit to the luminosity of stars (but also other objects, like accretion disks or active galactic nuclei, see below). Close to the Eddington luminosity, stars will start loosing their outer layers. For simplicity we work in spherical approximation. We assume we have an object of mass Mc which emits a luminosity L through a spherical surface with Radius R. The flux then is: resulting in the radiation pressure: (explanation: a single photon has a momentum of hν/c, summing over all photons and deviding by the area gives the pressure exerted by the photons if absorbed). If the gas is strongly ionized, the interaction between matter and photons can be approximated by the IMPRS Astrophysics Introductory Course Fall 2007 19 Thomson cross-section of e− and p: Therefore, the radiation pressure only works on the e− (but the protons get also accelerated because of electromagnetic coupling). A star will start disintegrating, if the accelerating force of the radiation is bigger than the force of gravitation: This defines the Eddington-Luminosity: or: IMPRS Astrophysics Introductory Course Fall 2007 20 4.3.2 Special Effects I: Winds and Thermal Pulses During the post main sequence phase stars loose a major part of their mass via winds and thermal pulses: main sequence 1 MΘ → tip of AGB 0.6 MΘ main sequence 8 MΘ → tip of AGB 0.8 MΘ The expelled gas is given back to the interstellar medium.
Recommended publications
  • The Evolution of Helium White Dwarfs: Applications to Millisecond

    The Evolution of Helium White Dwarfs: Applications to Millisecond

    Pulsar Astronomy — 2000 and Beyond ASP Conference Series, Vol. 3 × 108, 1999 M. Kramer, N. Wex, and R. Wielebinski, eds. The evolution of helium white dwarfs: Applications for millisecond pulsars T. Driebe and T. Bl¨ocker Max-Planck-Institut f¨ur Radioastronomie, Bonn, Germany D. Sch¨onberner Astrophysikalisches Institut Potsdam, Potsdam, Germany 1. White Dwarf Evolution Low-mass white dwarfs with helium cores (He-WDs) are known to result from mass loss and/or exchange events in binary systems where the donor is a low mass star evolving along the red giant branch (RGB). Therefore, He-WDs are common components in binary systems with either two white dwarfs or with a white dwarf and a millisecond pulsar (MSP). If the cooling behaviour of He- WDs is known from theoretical studies (see Driebe et al. 1998, and references therein) the ages of MSP systems can be calculated independently of the pulsar properties provided the He-WD mass is known from spectroscopy. Driebe et al. (1998, 1999) investigated the evolution of He-WDs in the mass range 0.18 < MWD/M⊙ < 0.45 using the code of Bl¨ocker (1995). The evolution of a 1 M⊙-model was calculated up to the tip of the RGB. High mass loss termi- nated the RGB evolution at appropriate positions depending on the desired final white dwarf mass. When the model started to leave the RGB, mass loss was virtually switched off and the models evolved towards the white dwarf cooling branch. The applied procedure mimicks the mass transfer in binary systems. Contrary to the more massive C/O-WDs (MWD ∼> 0.5 M⊙, carbon/oxygen core), whose progenitors have also evolved through the asymptotic giant branch phase, He-WDs can continue to burn hydrogen via the pp cycle along the cooling branch arXiv:astro-ph/9910230v1 13 Oct 1999 down to very low effective temperatures, resulting in cooling ages of the order of Gyr, i.
  • POSTERS SESSION I: Atmospheres of Massive Stars

    POSTERS SESSION I: Atmospheres of Massive Stars

    Abstracts of Posters 25 POSTERS (Grouped by sessions in alphabetical order by first author) SESSION I: Atmospheres of Massive Stars I-1. Pulsational Seeding of Structure in a Line-Driven Stellar Wind Nurdan Anilmis & Stan Owocki, University of Delaware Massive stars often exhibit signatures of radial or non-radial pulsation, and in principal these can play a key role in seeding structure in their radiatively driven stellar wind. We have been carrying out time-dependent hydrodynamical simulations of such winds with time-variable surface brightness and lower boundary condi- tions that are intended to mimic the forms expected from stellar pulsation. We present sample results for a strong radial pulsation, using also an SEI (Sobolev with Exact Integration) line-transfer code to derive characteristic line-profile signatures of the resulting wind structure. Future work will compare these with observed signatures in a variety of specific stars known to be radial and non-radial pulsators. I-2. Wind and Photospheric Variability in Late-B Supergiants Matt Austin, University College London (UCL); Nevyana Markova, National Astronomical Observatory, Bulgaria; Raman Prinja, UCL There is currently a growing realisation that the time-variable properties of massive stars can have a funda- mental influence in the determination of key parameters. Specifically, the fact that the winds may be highly clumped and structured can lead to significant downward revision in the mass-loss rates of OB stars. While wind clumping is generally well studied in O-type stars, it is by contrast poorly understood in B stars. In this study we present the analysis of optical data of the B8 Iae star HD 199478.
  • Arxiv:1910.04776V2 [Astro-Ph.SR] 2 Dec 2019 Lion Years

    Arxiv:1910.04776V2 [Astro-Ph.SR] 2 Dec 2019 Lion Years

    Astronomy & Astrophysics manuscript no. smsmax c ESO 2019 December 3, 2019 Letter to the Editor Maximally accreting supermassive stars: a fundamental limit imposed by hydrostatic equilibrium L. Haemmerle´1, G. Meynet1, L. Mayer2, R. S. Klessen3;4, T. E. Woods5, A. Heger6;7 1 Departement´ d’Astronomie, Universite´ de Geneve,` chemin des Maillettes 51, CH-1290 Versoix, Switzerland 2 Center for Theoretical Astrophysics and Cosmology, Institute for Computational Science, University of Zurich, Winterthurerstrasse 190, CH-8057 Zurich, Switzerland 3 Universitat¨ Heidelberg, Zentrum fur¨ Astronomie, Institut fur¨ Theoretische Astrophysik, Albert-Ueberle-Str. 2, D-69120 Heidelberg, Germany 4 Universitat¨ Heidelberg, Interdisziplinares¨ Zentrum fur¨ Wissenschaftliches Rechnen, Im Neuenheimer Feld 205, D-69120 Heidelberg, Germany 5 National Research Council of Canada, Herzberg Astronomy & Astrophysics Research Centre, 5071 West Saanich Road, Victoria, BC V9E 2E7, Canada 6 School of Physics and Astronomy, Monash University, VIC 3800, Australia 7 Tsung-Dao Lee Institute, Shanghai 200240, China Received ; accepted ABSTRACT Context. Major mergers of gas-rich galaxies provide promising conditions for the formation of supermassive black holes (SMBHs; 5 4 5 −1 & 10 M ) by direct collapse because they can trigger mass inflows as high as 10 − 10 M yr on sub-parsec scales. However, the channel of SMBH formation in this case, either dark collapse (direct collapse without prior stellar phase) or supermassive star (SMS; 4 & 10 M ), remains unknown. Aims. Here, we investigate the limit in accretion rate up to which stars can maintain hydrostatic equilibrium. −1 Methods. We compute hydrostatic models of SMSs accreting at 1 – 1000 M yr , and estimate the departures from equilibrium a posteriori by taking into account the finite speed of sound.
  • The Deaths of Stars

    The Deaths of Stars

    The Deaths of Stars 1 Guiding Questions 1. What kinds of nuclear reactions occur within a star like the Sun as it ages? 2. Where did the carbon atoms in our bodies come from? 3. What is a planetary nebula, and what does it have to do with planets? 4. What is a white dwarf star? 5. Why do high-mass stars go through more evolutionary stages than low-mass stars? 6. What happens within a high-mass star to turn it into a supernova? 7. Why was SN 1987A an unusual supernova? 8. What was learned by detecting neutrinos from SN 1987A? 9. How can a white dwarf star give rise to a type of supernova? 10.What remains after a supernova explosion? 2 Pathways of Stellar Evolution GOOD TO KNOW 3 Low-mass stars go through two distinct red-giant stages • A low-mass star becomes – a red giant when shell hydrogen fusion begins – a horizontal-branch star when core helium fusion begins – an asymptotic giant branch (AGB) star when the helium in the core is exhausted and shell helium fusion begins 4 5 6 7 Bringing the products of nuclear fusion to a giant star’s surface • As a low-mass star ages, convection occurs over a larger portion of its volume • This takes heavy elements formed in the star’s interior and distributes them throughout the star 8 9 Low-mass stars die by gently ejecting their outer layers, creating planetary nebulae • Helium shell flashes in an old, low-mass star produce thermal pulses during which more than half the star’s mass may be ejected into space • This exposes the hot carbon-oxygen core of the star • Ultraviolet radiation from the exposed
  • EVOLVED STARS a Vision of the Future Astron

    EVOLVED STARS a Vision of the Future Astron

    PUBLISHED: 04 JANUARY 2017 | VOLUME: 1 | ARTICLE NUMBER: 0021 research highlights EVOLVED STARS A vision of the future Astron. Astrophys. 596, A92 (2016) Loop Plume A B EDPS A nearby red giant star potentially hosts a planet with a mass of up to 12 times that of Jupiter. L2 Puppis, a solar analogue five billion years more evolved than the Sun, could give a hint to the future of the Solar System’s planets. Using ALMA, Pierre Kervella has observed L2 Puppis in molecular lines and continuum emission, finding a secondary source that is roughly 2 au away from the primary. This secondary source could be a giant planet or, alternatively, a brown dwarf as massive as 28 Jupiter masses. Further observations in ALMA bands 9 or 10 (λ ≈ 0.3–0.5 mm) can help to constrain the companion’s mass. If confirmed as a planet, it would be the first planet around an asymptotic giant branch star. L2 Puppis (A in the figure) is encircled by an edge-on circumstellar dust disk (inner disk shown in blue; surrounding dust in orange), which raises the question of whether the companion body is pre-existing, or if it has formed recently due to accretion processes within the disk. If pre-existing, the putative planet would have had an orbit similar in extent to that of Mars. Evolutionary models show that eventually this planet will be pulled inside the convective envelope of L2 Puppis by tidal forces. The companion’s interaction with the star’s circumstellar disk has invoked pronounced features above the disk: an extended loop of warm dusty material, and a visible plume, potentially launched by accretion onto a disk of material around the planet itself (B in the figure).
  • Jsolated Stars of Low Metallicity

    Jsolated Stars of Low Metallicity

    galaxies Article Jsolated Stars of Low Metallicity Efrat Sabach Department of Physics, Technion—Israel Institute of Technology, Haifa 32000, Israel; [email protected] Received: 15 July 2018; Accepted: 9 August 2018; Published: 15 August 2018 Abstract: We study the effects of a reduced mass-loss rate on the evolution of low metallicity Jsolated stars, following our earlier classification for angular momentum (J) isolated stars. By using the stellar evolution code MESA we study the evolution with different mass-loss rate efficiencies for stars with low metallicities of Z = 0.001 and Z = 0.004, and compare with the evolution with solar metallicity, Z = 0.02. We further study the possibility for late asymptomatic giant branch (AGB)—planet interaction and its possible effects on the properties of the planetary nebula (PN). We find for all metallicities that only with a reduced mass-loss rate an interaction with a low mass companion might take place during the AGB phase of the star. The interaction will most likely shape an elliptical PN. The maximum post-AGB luminosities obtained, both for solar metallicity and low metallicities, reach high values corresponding to the enigmatic finding of the PN luminosity function. Keywords: late stage stellar evolution; planetary nebulae; binarity; stellar evolution 1. Introduction Jsolated stars are stars that do not gain much angular momentum along their post main sequence evolution from a companion, either stellar or substellar, thus resulting with a lower mass-loss rate compared to non-Jsolated stars [1]. As previously stated in Sabach and Soker [1,2], the fitting formulae of the mass-loss rates for red giant branch (RGB) and asymptotic giant branch (AGB) single stars are set empirically by contaminated samples of stars that are classified as “single stars” but underwent an interaction with a companion early on, increasing the mass-loss rate to the observed rates.
  • Evolution of Thermally Pulsing Asymptotic Giant Branch Stars

    Evolution of Thermally Pulsing Asymptotic Giant Branch Stars

    The Astrophysical Journal, 822:73 (15pp), 2016 May 10 doi:10.3847/0004-637X/822/2/73 © 2016. The American Astronomical Society. All rights reserved. EVOLUTION OF THERMALLY PULSING ASYMPTOTIC GIANT BRANCH STARS. V. CONSTRAINING THE MASS LOSS AND LIFETIMES OF INTERMEDIATE-MASS, LOW-METALLICITY AGB STARS* Philip Rosenfield1,2,7, Paola Marigo2, Léo Girardi3, Julianne J. Dalcanton4, Alessandro Bressan5, Benjamin F. Williams4, and Andrew Dolphin6 1 Harvard-Smithsonian Center for Astrophysics, 60 Garden St., Cambridge, MA 02138, USA 2 Department of Physics and Astronomy G. Galilei, University of Padova, Vicolo dell’Osservatorio 3, I-35122 Padova, Italy 3 Osservatorio Astronomico di Padova—INAF, Vicolo dell’Osservatorio 5, I-35122 Padova, Italy 4 Department of Astronomy, University of Washington, Box 351580, Seattle, WA 98195, USA 5 Astrophysics Sector, SISSA, Via Bonomea 265, I-34136 Trieste, Italy 6 Raytheon Company, 1151 East Hermans Road, Tucson, AZ 85756, USA Received 2016 January 1; accepted 2016 March 14; published 2016 May 6 ABSTRACT Thermally pulsing asymptotic giant branch (TP-AGB) stars are relatively short lived (less than a few Myr), yet their cool effective temperatures, high luminosities, efficient mass loss, and dust production can dramatically affect the chemical enrichment histories and the spectral energy distributions of their host galaxies. The ability to accurately model TP-AGB stars is critical to the interpretation of the integrated light of distant galaxies, especially in redder wavelengths. We continue previous efforts to constrain the evolution and lifetimes of TP-AGB stars by modeling their underlying stellar populations. Using Hubble Space Telescope (HST) optical and near-infrared photometry taken of 12 fields of 10 nearby galaxies imaged via the Advanced Camera for Surveys Nearby Galaxy Survey Treasury and the near-infrared HST/SNAP follow-up campaign, we compare the model and observed TP- AGB luminosity functions as well as the ratio of TP-AGB to red giant branch stars.
  • Isotopic Imprints of Super-Agb Stars and Their Supernovae in the Solar System

    Isotopic Imprints of Super-Agb Stars and Their Supernovae in the Solar System

    82nd Annual Meeting of The Meteoritical Society 2019 (LPI Contrib. No. 2157) 6424.pdf ISOTOPIC IMPRINTS OF SUPER-AGB STARS AND THEIR SUPERNOVAE IN THE SOLAR SYSTEM. L. R. Nittler, Dept. of Terrestrial Magnetism, Carnegie Institution of Washington, 5241 Broad Branch Rd NW, Washington DC 20015, USA ([email protected]) Introduction: In studies of the origin of presolar grains and bulk nucleosynthetic isotopic anomalies in meteorites, little attention has been paid to the potential importance of stars in the mass range of ~8-10 solar masses. These stars lie in a middle-ground between low- and intermediate mass asymptotic giant branch (AGB) stars that end their lives as white dwarfs and massive stars whose cores burn all the way to Fe before collapsing and exploding as supernovae (SNII), leaving behind neutron stars or black holes. They evolve through a “super-AGB” phase, undergoing thousands of thermal pulses and losing most of their mass in strong winds [1]. However, their final fates (e.g., as white dwarfs versus neutron stars following core-collapse supernovae) depend on highly uncertain physics and diagnostic observable signatures of both super-AGB stars and their possible supernovae are controversial [1, 2]. Here we discuss possible ways super-AGB stars and their supernovae may have left nucleosynthetic imprints in the solar system. Super-AGB stars: Although most presolar SiC, silicate and oxide stardust grains are inferred to have originated in AGB stars [3], the isotopic signatures largely point to relatively low-mass (~1-3 M) progenitors. Until recently, intermediate-mass (4-8M) AGB stars have largely been ruled out as parent stars because their predicted O isotopic ratios are not observed.
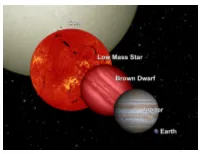
  • The Coolest Brown Dwarfs

    The Coolest Brown Dwarfs

    ClassY - The Coolest Brown Dwarfs CFBDS J005910.90-011401.3 – T9/Y0 - first class Y, 30 light-years distance, Temp 620K, Mass 15-30 M_Jup WISE 0855−0714 – Y2 - coolest at Temp ~ 250K, 7.3 light-years distance, Mass 3-10 M_Jup ClassY - The Coolest Brown Dwarfs CFBDS J005910.90-011401.3 – T9/Y0 - first class Y, 30 light-years distance, Temp 620K, Mass 15-30 M_Jup WISE 0855−0714 – Y2 - coolest at Temp ~ 250K, 7.3 light-years distance, Mass 3-10 M_Jup Why are all brown dwarf stars about the same size, even if the mass ranges from 10-500 M_Jup? Stellar evolution so far Different energy sources during different stages in the star's evolution Protostar phase (KH contraction) MS phase H->He RGB phase (shell H->He) And remember: more massive stars evolve faster during all stages What is this Plot Showing? globular cluster Announcements • Today – More low mass stellar evolution • Thursday – High mass stellar evolution and HW#4 is due • Tuesday Feb 25 – Review • Thursday Feb 27 – Exam#1 Intrinsic variability • Those that vary in brightness as a result of conditions within the star itself. • Found in the instability strip. Any star within these portions of the H-R diagram will become unstable to pulsations. • The different regions produce different kinds of observed phenomena. • Stars may go through these stages several times during their lives. Cause of pulsations • Stars are variable because they are unstable in one way or another: they lack hydrostatic equilibrium beneath surface. • Miras are not well understood, but other, more periodically varying stars are better understood, like the Cepheids: • The ionization zone of He lies at a distance from the center of the star, close to the surface.
  • Variability Morphologies in the Color-Magnitude Diagram

    Variability Morphologies in the Color-Magnitude Diagram

    Variability Morphologies In The Color‐Magnitude Diagram Searching For Secular Variability Maxime Spano, Nami Mowlavi, Laurent Eyer, Gilbert Burki Geneva Observatory, University of Geneva, 51 Chemin des Maillettes, CH-1290 Sauverny, Switzerland Abstract. This work is part of an effort to detect secular variable objects in large scale surveys by analysing their path in color‐magnitude diagrams. To this aim, we first present the variability morphologies in the V/V‐I diagram of several types of variable stars. They comprise both periodic and non periodic variable stars from the Large Magellanic Cloud, such as classical Cepheids, long period variables or Be and R Coronae Borealis stars, as well as two of the detected secular variable stars in the Galaxy, FG Sge and V4334 Sgr. The study of the different variability morphologies allows the identification of regions in the color‐magnitude diagram where those secular variable stars could be detected. We also estimate the number of such secular variable stars expected in the Large Magellanic Cloud. Keywords: color-magnitude diagram; individual: FG Sge, V4334 Sgr, LMC. PACS: 97.10.Zr; 97.10.Sw; 98.56.Si. INTRODUCTION nearby galaxies are thus favored. OGLE‐II and III surveys of the LMC, providing BVI photometry for At some evolutionary phases, the stellar evolution resp. 7 and 35 millions stars (Udalski et al. 1997, timescale becomes comparable to the human lifetime. Udalski et al. 2000, Szymański 2005, Udalski et al. The evolution of these stars, called secular variable 2008) have been chosen here. All the variable stars stars, then becomes detectable in real time, providing a identified so far in the OGLE database are plotted in unique way to directly compare observations with the V/V‐I CMD shown in Fig.
  • U Antliae — a Dying Carbon Star

    U Antliae — a Dying Carbon Star

    THE BIGGEST, BADDEST, COOLEST STARS ASP Conference Series, Vol. 412, c 2009 Donald G. Luttermoser, Beverly J. Smith, and Robert E. Stencel, eds. U Antliae — A Dying Carbon Star William P. Bidelman,1 Charles R. Cowley,2 and Donald G. Luttermoser3 Abstract. U Antliae is one of the brightest carbon stars in the southern sky. It is classified as an N0 carbon star and an Lb irregular variable. This star has a very unique spectrum and is thought to be in a transition stage from an asymptotic giant branch star to a planetary nebula. This paper discusses possi- ble atomic and molecular line identifications for features seen in high-dispersion spectra of this star at wavelengths from 4975 A˚ through 8780 A.˚ 1. Introduction U Antliae (U Ant = HR 4153 = HD 91793) is classified as an N0 carbon star with a visual magnitude of 5.38 and B−V of +2.88 (Hoffleit 1982). It also is classified as an Lb irregular variable with small scale light variations. Scattered light optical images for U Ant have been made and these observations are consistent the existence of a geometrically thin (∼3 arcsec) spherically symmetric shell of radius ∼43 arcsec. The size of this shell agrees very well with that of the detached shell seen in CO radio line emission. These observations also show the presence of at least one, possibly two, shells inside the 43 arcsec shell (Gonz´alez Delgado et al. 2001). In this paper, absorption lines in the optical spectrum of U Ant are tentatively identified for this bright cool carbon star.
  • ASTR3007/4007/6007, Class 10: Low Mass Stellar Evolution 24 March

    ASTR3007/4007/6007, Class 10: Low Mass Stellar Evolution 24 March

    ASTR3007/4007/6007, Class 10: Low Mass Stellar Evolution 24 March Our topic for today is the first of three classes about post-main sequence evolution. Today the topic is low mass stars, with the line between low and high mass to be discussed in a bit. I. Leaving the Main Sequence A. Main Sequence Lifetime Stars remain on the main sequence as long as their hydrogen fuel lasts. While on the main sequence, their properties do not change much, but they do change some due to the gradual conversion of H into He. As a result of this conversion, the hydrogen mass fraction X decreases, while the helium mass fraction Y increases. As a result, the mean atomic weight changes. Recall that 1 1 1 − X − Y ≈ X + Y + (1) µI 4 hAi 1 1 ≈ (1 + X) (2) µe 2 1 1 1 = + : (3) µ µI µe Insterstellar gas out of which stars forms has roughly X = 0:74 and Y = 0:24 (in contrast to X = 0:707 and Y = 0:274 in the Sun, which has processed some of its H into He), which gives µ = 0:60. In contrast, once all the H has been turned into He, X = 0 and Y = 0:98, which gives µ = 1:34. In stars like the Sun that are radiative in their cores, the changes occur shell by shell, so different shells have different compositions depending on their rate of burning. In stars that are convective in their cores, convection homogenises the composition of the different shells, so the entire convective core has a uniform composition.