Semi Empirical Formula for Neutrinoless Double Beta Decay
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Rticulars of Organization, Function and Duties of Passport Office, Kozhikode
PASSPORT OFFICE, KOZHIKODE RIGHT TO INFORMATION Disclosure of Information under Section 4(1)(b) of the Right to Information Act, 2005 in respect of Passport Office, Kozhikode. Section (4) (1) (b) (i): Particulars of organization, function and duties of Passport Office, Kozhikode. HISTORICAL BACKGROUND The Regional Passport Office, Kozhikode started functioning in June, 1978 to facilitate expeditious issue of passport to the applicants belonging to the Malabar region of Kerala, residing in the districts of Palakkad, Malappuram, Kozhikode, Wayanad, Kannur, Kasaragod and Mahe district of Puducherry. This office was subsequently bifurcated and created a new Passport Office at Malappuram with effect from 28th August, 2006, taking away Palakkad and Malappuram districts. Subsequently the Palakkad district was merged with RPO, Cochin. Later, the Passport Office, Malappuram was merged with this office. Thus, this office now caters to the applicants from the five northern districts of Kerala, viz., Malappuram, Kozhikode, Wayanad, Kannur, Kasaragod and Mahe region of Puducherry (Union Territory). Consequent on implementation of the Passport Seva Project, passport applications are being accepted at Passport Seva Kendra (PSK) and Post Office Passport Seva Kenda (POPSK). Five PSK and one POPSK are functioning under the jurisdiction of this office as depicted below. No. PSK / POPSK Place 1 PSK No.1 Kannur 2 PSK No.2 Kozhikode (West Hill) 3 PSK No.3 Vatakara 4 PSK No.4 Payyanur 5 PSK No.5 Malappuram 6 POPSK Kasaragod (HPO) Passport applicants can log on to website: www.passportindia.gov.in for online registration of passport applications. ORGANISATION CHART The Regional Passport Office, Kozhikode has a total of 80 staff as depicted below: Sl.No. -

SFD Report Kannur India
SFD Report Kannur India Final Report This SFD Report was created through field-based research by Centre for Science and Environment (CSE) as part of the SFD Promotion Initiative Date of production: 29/11/2016 Last update: 29/11/2016 Kannur Executive Summary Produced by: CSE India SFD Report Kannur, India, 2017 Produced by: Suresh Kumar Rohilla, CSE Bhitush Luthra, CSE Anil Yadav, CSE Bhavik Gupta, CSE ©Copyright The tools and methods for SFD production were developed by the SFD Promotion Initiative and are available from: www.sfd.susana.org. All SFD materials are freely available following the open-source concept for capacity development and non-profit use, so long as proper acknowledgement of the source is made when used. Users should always give credit in citations to the original author, source and copyright holder. Last Update: 29/12/2016 I Kannur Executive Summary Produced by: CSE India 1. The graphic 2. Diagram information 3. General city information Desk or field based: Kannur, also known by its English name Cannanore, is a city in Kannur district, state of Comprehensive Kerala, India. It is the administrative headquarters Produced by: of the Kannur district and situated 518 km north of the state capital Thiruvananthapuram. Kannur is Centre for Science and Environment (CSE), New famous for its pristine beaches, Theyyam, (its Delhi native performing art), and its handloom industry. Status: Kannur Municipal Corporation (KMC) is the largest urban local body of the north Malabar region. This is a final SFD On 1st November 2015, the ‘Kannur Municipality’ Date of production: was combined with five adjacent gram panchayats (Pallikkunnu, Puzhathi, Elayavoor, Edakkad & 02/01/2017 Chelora) and became KMC. -

Accused Persons Arrested in Kannur District from 12.03.2017 to 18.03.2017
Accused Persons arrested in Kannur district from 12.03.2017 to 18.03.2017 Name of the Name of Name of the Place at Date & Court at Sl. Name of the Age & Cr. No & Sec Police Arresting father of Address of Accused which Time of which No. Accused Sex of Law Station Officer, Rank Accused Arrested Arrest accused & Designation produced 1 2 3 4 5 6 7 8 9 10 11 POOKOTHNAD 12.03.17 AT 405/17 118(a) 1 SURESH K GOPALAN 33/17 KOLIYATTU VALAPPIL Taliparamba VINEESH VR BAILED A 00.25 KP ACT POOKOTHNAD 12.03.17 AT 406/17 279,IPC 2 KALESH VV RAJAN 20/17 PUZHAKKULANGARA Taliparamba BINUMOHAN BAILED A 10.25 185 M V ACT 407/17 U/S 279 12.03.17 AT 3 VIPIN K NARAYANAN 33/17 KUTTIKKOL CHIRAVAKKU IPC 185 OF MV TALIPARAMBA PREMARAJAN BAILED 18.05 ACT 408/18 U/S 279 ANEESH 12.03.17 AT 4 KRISHNAN 44/17 CHAVANAPPUZHA EZHAM MILE IPC 185 OF MV TALIPARAMBA MOHANAN BAILED KUMAR 18.40 ACT 409/17 U/S 279 12.03.17 AT 5 RATHEESH RAJAN 36/17 THALORA NEWS KORNAR IPC 185 OF MV TALIPARAMBA BINUMOHAN BAILED 19.45 ACT 410/17 U/S 12.03.17 AT 6 RINAS MUSTAFA 26/17 MANNA NEWS KORNAR 279IPC 118 e of TALIPARAMBA BINUMOHAN BAILED 21.00 KP ACT 411/17 U/S 15 C 12.03.17 AT 7 MUKUNDAN GOPALAN 38/17 CHAVANAPPUZHA KAKKATHODE R/W 63 OF TALIPARAMBA BINUMOHAN BAILED 21.30 ABKARI ACT 411/17 U/S 15 C RAMAKRISHNA 12.03.17 AT 8 AKHIL 24/17 THADIKKADAVU KAKKATHODE R/W 63 OF TALIPARAMBA BINUMOHAN BAILED N 21.30 ABKARI ACT 411/17 U/S 15 C ABDUL 12.03.17 AT 9 MOLDU 37/17 THADIKKADAVU KAKKATHODE R/W 63 OF TALIPARAMBA BINUMOHAN BAILED RASAQUE 21.30 ABKARI ACT 411/17 U/S 15 C 12.03.17 AT 10 ANSAR KV -

Requiring Body SIA Unit
SOCIAL IMPACT ASSESSMENT STUDY FINAL REPORT LAND ACQUISITION FOR THE CONSTRUCTION OF OIL DEPOT &APPROACH ROAD FOR HPCL/BPCL AT PAYYANUR VILLAGE IN KANNUR DISTRICT 15th JANUARY 2019 Requiring Body SIA Unit RAJAGIRI outREACH HINDUSTAN PETROLEUM Rajagiri College of Social Sciences CORPORATION LTD. Rajagiri P.O, Kalamassery SOUTHZONE Pin: 683104 Phone no: 0484-2550785, 2911332 www.rajagiri.edu 1 CONTENTS CHAPTER 1 EXECUTIVE SUMMARY 1.1 Project and Public Purpose 1.2 Location 1.3 Size and Attributes of Land Acquisition 1.4 Alternatives Considered 1.5 Social Impacts 1.6. Mitigation Measures CHAPTER 2 DETAILED PROJECT DESCRIPTION 2.1. Background of the Project including Developers background 2.2. Rationale for the Project 2.3. Details of Project –Size, Location, Production Targets, Costs and Risks 2.4. Examination of Alternatives 2.5. Phases of the Project Construction 2.6.Core Design Features and Size and Type of Facilities 2.7. Need for Ancillary Infrastructural Facilities 2.8.Work force requirements 2.9. Details of Studies Conducted Earlier 2.10 Applicable Legislations and Policies CHAPTER 3 TEAM COMPOSITION, STUDY APPROACH AND METHODOLOGY 3.1 Details of the Study Team 3.2 Methodology and Tools Used 3.3 Sampling Methodology Used 3.4. Schedule of Consultations with Key Stakeholders 3.5. Limitation of the Study CHAPTER 4 LAND ASSESSMENT 4.1 Entire area of impact under the influence of the project 4.2 Total Land Requirement for the Project 4.3 Present use of any Public Utilized land in the Vicinity of the Project Area 2 4.4 Land Already Purchased, Alienated, Leased and Intended use for Each Plot of Land 4.5. -

Kannur School Code Sub District Name of School School Type 13001 Govt H S Pulingome G 13002 St. Marys H S Cherupuzha a 13003 St
Kannur School Code Sub District Name of School School Type 13001 Govt H S Pulingome G 13002 St. Marys H S Cherupuzha A 13003 St. Josephs English High School P 13004 Govt V H S S for Girls Kannur G 13005 Govt V H S S Kannur G 13006 ST TERESAS AIHSS KANNUR A 13007 ST MICHAELS AIHSS KANNUR A 13008 TOWN GHSS KANNUR G 13009 Govt. City High School, Kannur G 13010 DIS GIRLS HSS KANNUR CITY A 13011 Deenul Islam Sabha E M H S P 13012 GHSS PALLIKUNNU G 13013 CHOVVA HSS, CHOVVA A 13014 CHM HSS ELAYAVOOR A 13015 Govt. H S S Muzhappilangad G 13016 GHSS THOTTADA G 13017 Azhikode High School, Azhikode A 13018 Govt. High School Azhikode G 13019 Govt. Regional Fisheries Technical H S G 13020 CHMS GOVT. H S S VALAPATTANAM G 13021 Rajas High School Chirakkal A 13022 Govt. High School Puzhathi G 13023 Seethi Sahib H S S Taliparamba A 13024 Moothedath H S Taliparamba A 13025 Tagore Vidyanikethan Govt. H S S G 13026 GHSS KOYYAM G 13027 GHSS CHUZHALI G 13028 Govt. Boys H S Cherukunnu G 13029 Govt. Girls V H S S Cherukunnu G 13030 C H M K S G H S S Mattool G 13032 Najath Girls H S Mattool North P.O P 13033 Govt. Boys High School Madayi G 13034 Govt. H S S Kottila G 13035 Govt. Higher Secondary School Cheruthazham G 13036 Govt. Girls High School Madayi G 13037 Jama-Ath H S Puthiyangadi A 13038 Cresent E M H S Mattambram P 13039 Govt. -

District Functionaries
DISTRICT FUNCTIONARIES KANNUR . DT (STD CODE- 0497 ) SLNO DESIGNATION OFFICE PHONE/FAX MOBILE(CUG) E-MAIL ID 1DISTRICT COLLECTOR 4972700243 / 04972700243 9447029015 [email protected] 2 DISTRICT POLICE CHIEF 4972763330 / 04972763330 9497996973 [email protected] 3 DY. COLLECTOR(ELECTION) 04972709140 / 04972709140 8547616032 [email protected] 4 JS (ELECTION) 04972709140 / 04972709140 [email protected] 5 ELECTION ASSISTANT 04972709140 / 04972709140 [email protected] MUNICIPAL CORPORATION - KANNUR NAME OF OFFICE PHONE MOBILE SLNO DETAILS DESIGNATION EMAIL ID CORPORATION NO /FAX (CUG) District Officer, Scheduled Caste Development , 1 KANNUR NAME OF RO1 Kannur 0497-2 700596 [email protected] General Manager, NAME OF RO2 DIC, Kannur 4972700928 [email protected] NAME OF ERO Radhakrishnan P Corporation Secretary 4972700234 9447964037 [email protected] MUNICIPALITIES - KANNUR NAME OF OFFICE PHONE MOBILE DETAILS DESIGNATION EMAIL ID MUNICIPALITY NO /FAX (CUG) EXECUTIVE ENGINEER- 1 THALASSERY NAME OF RO1 PAZHZSSI SULAIKHA A M IRRIGATION 0490-2700487 9846975483 [email protected] DT. REGISTRAR NAME OF RO2 MADHU R (GENERAL) 0490-2321330 9447318559 [email protected] NAME OF ERO SUBHAGAN A S SECRETARY 0490-2342052 9447458432 [email protected] Deputy conservator of 2 MATTANNUR NAME OF RO1 SUNEEL PAMIDI forest 0497-2704808 [email protected] NAME OF RO2 Assistant Conservator A.P.IMTHYAS of forest Kannur 4972709105 [email protected] NAME OF ERO SURESHAN.M SECRETARY 0490-2471226 -

15 -ാം േകരള നിയമസഭ 1 -ാം സേ ളനം ന ചി ം ഇ ാ േചാദ ം നം . 138 07-06
15 -ാം േകരള നിയമസഭ 1 -ാം സേളനം ന ചിം ഇാ േചാദം നം. 138 07-06-2021 - ൽ മപടി് ളയിൽ തകർ േറാകൾ േചാദം ഉരം Shri M. V. Govindan Master ീ . സി േജാസഫ് (തേശസയംഭരണം ാമവികസനം എൈം വ് മി) (എ) (എ) 2018, 2019 വർഷിൽ ഉായ ളയിൽ 2018, 2019 വർഷളിൽ ഉായ ളയിൽ തകർ കർ ജിയിെല േറാകെട എം തകർ ാമീണ േറാകൾ എ; അവ 877 ആണ്. േറാകൾ് 109.236 േകാടി ഏെതാെ; എ േകാടിെട നാശനളാണ് പെട നാശനളാണ് ഉായിത്. േറാകൾ് ഉായിത്; ത ത േറാകൾക് 76.289181 േകാടി പ േറാകൾ് ഫ് അവദിിോ; ഉെിൽ അവദിി്. ത േറാകെടം എ ക ഏെതാം േറാകൾെ് അവദി കെടം വിശദാംശൾ യഥാമം വിശദമാേമാ; അബം I, II എിവയിൽ കാണാതാണ് . (ബി) ളയിൽ തകർ പല ാമീണ േറാകം (ബി) നവീകരിതിന് ഫ് അവദിാത് ളയിൽ തകർ ാമീണ േറാകൾ യിൽെിോ: ആയ നവീകരിതിനാവശമായ നടപടികൾ സീകരി നവീകരിതിനാവശമായ നടപടി വരികയാണ്. സീകരിേമാ? െസൻ ഓഫീസർ 1 of 1 LSGD DIVISION, KANNUR LSGD SUB DIVISION, TALIPARAMBA BLOCK PANCHAYATH LIST OF ROADS, CULVERTS & BRIDGES DAMAGED DURING FLOOD 2018 Name of Width of Road Name of Block Length of Road Width of Carriage way Sl No Name of Constituency Panchayath/Muncipality/C Name of Road, Bridge, Culvert, Building (in m) Amount Remarks Panchayath (in km) (in m) orporation RoW=Right of Way 0 1 2 3 4 5 6 7 ₹8 12 300 m concrere drain is proposed since there is no RoW greater than 3.0m & 1 Irikkoor Thaliparamba Udayagiri GP Anakkuzhi-Kappimala 0.3 3.00m ₹10,00,000 outlet available retarring less than 5.5m works are also to be arranged One culvert is to be constructed in the given RoW greater than 3.0m & chainage and road work for 2 Irikkoor Thaliparamba Udayagiri GP Mampoyil - Kanayankalpadi 1 3.00m ₹11,46,810 less than 5.5m the completely destroyed portions were arranged by GP Densily populated region RoW greater than 3.0m & majority of the dwellers 3 Irikkoor Thaliparamba Udayagiri GP Munderithatt - Thalathanni Road 1 3.00m ₹10,00,000 less than 5.5m belongs to Backward Community Concrete Drains,side RoW greater than 3.0m & protections works and pipe 4 Irikkoor Thaliparamba Udayagiri GP Kattappalli-Sreegiri-Mukkuzhi road 1.3 3.00m ₹5,00,000 less than 5.5m culverts are to be constructed. -

Annur, a Village Which Plays Chef
A village which plays chef www.bekaltourism.com www.bekaltourism.com TAnnurhe vegetarian and non-vegetarian dishes of north Kerala are world famous, and among them the most sought-after are the traditionally prepared vegetarian dishes of the village of Annur in north Malabar. Annur is situated in the small town of Payyanur in Kannur district. The cooks of the region are so talented that they can send foodies to peaks of gustatory delight with their indigenous methods of preparation. www.bekaltourism.com The most mouth-watering dish on offer at Annur is green gram pudding. The main ingredients are green gram, high quality jaggery and ghee [clarified butter]. The culinary artist works his ultimate magic when he adds dry ginger powder, cardamom powder and golden, ghee-roasted cashews. Unlike other parts of Kerala, Annur village does not add raisins in this pudding. This is to prevent the sourness of raisins to upset the delicate taste of the pudding as it cools. www.bekaltourism.com Koottu kari is a sure item in any traditional feast in north Malabar. Of all the varieties prepared across Kerala, the Annur version is easily the best. It is as though yam and raw banana, the chief vegetables used in Koottu kari, yield their special flavours only to the Annur chefs. Annur village in north Malabar waits patiently for connoisseurs who wander in search of dishes that will pamper their palates. Green gram pudding and Koottu kari are not the only items that woo such gustatory nomads. There is a mind-boggling variety that has the power to send every gourmet into a virtual journey of taste-experiences. -

REPORT of FIELD VISIT Submitted by Shijina.K Multi Tasking Personnel
REPORT OF FIELD VISIT Submitted by Shijina.K Multi tasking personnel- NULM Mattanur Municipality .Kannur I visited different functional areas of Kudumbasree mission including CDS, Kudumbasree NHG unit, micro enterprises, Asraya benefiaciary, JLG group and had a discussion with the unit authorities. The general information was collected by me with the help of unstructured questionnaire and observation. The data was collected regarding number of unit members, source of income, their activities etc. Details are mentioned below., Orma Kudumbasree Orma Kudumbasree unit was started its functioning in the year 2014 in Maruthayi, under Mattannur Municipality.There are 20 members in the unit. 5 members are selected for undertaking various activities including health infrastructure etc.Meetings are convened on a weekly basis in the houses of Kudumbasree members. In the weekly meeting all the members are bring their thrift which will be collected. In the meeting various problems faced by the group members are discussed along with suggestions to improve the situations.Oruma kudumbasree linked with Porora Cooperative bank, Maruthayi. Members are allowed to take loan from their thrift. Asraya Pallikara Mathu one of the Asraya beneficiary of Mattannur Municipality lives in Payyeparamb. There are 3 members in her family.All are females.They are economically backward. She gets food grains, medical care and support from Asraya project. She looked so happy when she saw me. I always grateful to CDS member Mrs.Roja for her continuous support to see clear change in the lives of that family. She works as a mediator between CDS and Asraya beneficiary. She give full support and care for this women. -
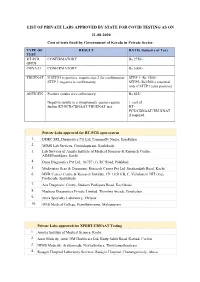
LIST of PRIVATE LABS APPROVED by STATE for COVID TESTING AS on 21-08-2020 Cost of Tests Fixed by Government of Kerala in Private Sector
LIST OF PRIVATE LABS APPROVED BY STATE FOR COVID TESTING AS ON 21-08-2020 Cost of tests fixed by Government of Kerala in Private Sector. TYPE OF RESULT RATE( Inclusive of Tax) TEST RT-PCR CONFIRMATORY Rs 2750/- OPEN CBNAAT CONFIRMATORY Rs 3000/- TRUENAT If STEP1 is positive, require step 2 for confirmation STEP 1- Rs 1500/- STEP 1 negative is confirmatory STEP2- Rs1500/-( required only if STEP1 turns positive) ANTIGEN Positive results are confirmatory. Rs 625/- Negative results in a symptomatic person require + cost of further RT-PCR/CBNAAT/TRUENAT test RT- PCR/CBNAAT/TRUENAT if required Private Labs approved for RT-PCR open system 1. DDRC SRL Diagnostics Pvt Ltd, Panampilly Nagar, Ernakulam 2. MIMS Lab Services, Govindapuram, Kozhikode 3. Lab Services of Amrita Institute of Medical Sciences & Research Centre, AIMSPonekkara, Kochi 4. Dane Diagnostics Pvt Ltd, 18/757 (1), RC Road, Palakkad 5. Medivision Scan & Diagnostic Research Centre Pvt Ltd, Sreekandath Road, Kochi 6. MVR Cancer Centre & Research Institute, CP 13/516 B, C, Vellalaserri NIT (via), Poolacode, Kozhikode 7. Aza Diagnostic Centre, Stadium Puthiyara Road, Kozhikode 8. Neuberg Diagnostics Private Limited, Thombra Arcade, Ernakulam 9. Jeeva Specialty Laboratory, Thrissur 10. MES Medical College, Perinthalmanna, Malappuram Private Labs approved for XPERT/CBNAAT Testing 1. Amrita Institute of Medical Science, Kochi 2. Aster Medcity, Aster DM Healthcare Ltd, Kutty Sahib Road, Kothad, Cochin 3. NIMS Medicity, Aralumoodu, Neyyattinkara, Thiruvananthapuram 4. Rajagiri Hospital Laboratory Services, Rajagiri Hospital, Chunangamvely, Aluva 5. Micro Health LAbs, MPS Tower, Kozhikode 6. Believers Church Medical College Laboratory, St Thomas Nagar, Kuttapuzha P.O., Thiruvalla 7. -

Accused Persons Arrested in Kannur District from 16.06.2019To22.06.2019
Accused Persons arrested in Kannur district from 16.06.2019to22.06.2019 Name of Name of the Name of the Place at Date & Arresting Court at Sl. Name of the Age & Cr. No & Sec Police father of Address of Accused which Time of Officer, which No. Accused Sex of Law Station Accused Arrested Arrest Rank & accused Designation produced 1 2 3 4 5 6 7 8 9 10 11 Manoj.V.V, Pappinisseri Cr.No.583/19 Inspector of 22/19 V.V.House, 16.06.2019 Valapattana Released on 1 Abijitj Anil Anil Kumar Amsom, U/s.118(a) of Police, Male Pappinisseri at 19.34 hrs m bail Kattilepalli KP Act. Valapattanam PS Valapttanam Cr.No.581/19 Vijayakumar, SI 23/19 Madakkudiyan House, 16.06.2019 Valapattana Released on 2 Jishnu.P Damodaran Amsom, U/s. 279 IPC & of Police, male Pappinisseri at 18.17 hrs m bail Kalarivathukkal 185 of MV Act. Valapattanam Madathil Thayyil Chirakkal Cr.No. 580/19 Vijayakumar, SI Shaji Madathil 36/19 16.06.2019 Valapattana Released on 3 Janardhanan House, Chalil, Amsom, U/s. 279 IPC & of Police, Thayyil male at 16.50 hrs m bail Azheekode Kottakkunnu 185 of MV Act Valapattanam Nr Cr no 470/19 Sujith kumar c 45/19,M Sangam quarters, 2019-06- Santhosh k, Si Bailed By 4 Aravindan gurusannidhi, u/s 279 ipc & Panur k ale muliyil nada, kodiyeri 16T21:45 panoor ps Police Vallangad 185 of kp act Cr no 469/19 19/19, Kuttikkattil house, Nr kkvm hss, 2019-06- Santhosh k, Si Bailed By 5 Abhishek t Babu thilakan u/s 279 ipc & Panur Male champad po panoor 16T20:45 panoor ps Police 185 of kp act Saif mahal, Pannyannur Cr no 468/19 Munavar Basheer 27/19, 2019-06- -

SALT SATYAGRAHA in MALABAR - a HISTORICAL ANALYSIS Vimal Kumar.C.L
SALT SATYAGRAHA IN MALABAR - A HISTORICAL ANALYSIS Vimal Kumar.C.L. Assistant Professor, Department of History, K.N.M. Government College, Kanjiramulam Abstract The Salt Satyagraha was started under the leadership of Mahatma Gandhi in March 1930 had its repercussions in Malabar also. Payyanur was the primary setting of Salt Satyagraha in Malabar. A few bunches of Satyagrahis from Kozhikode, Palakkad and different parts of Kerala walked to Payyanur to partake in the battle. Many best pioneers like K.Kelappan, Muhammad Abdur Rahiman, and K. Madhavan Nair captured for infringing upon salt-law and condemned them to thorough detainment. Salt March Kerala was composed under the flag of Kerala Pradesh Congress Committees. It was an impression of the Civil Disobedience Movement in India. The salt Satyagraha in Malabar brought a feeling of solidarity of among the general population in Malabar as well as in Travancore-Cochin. It supported the general population in their battle for the opportunity. Daily papers likewise assumed a noticeable part to spread the thoughts of the satyagrhis towards the ordinary citizens. Satyagraha additionally made a feeling of oneness among the general population. It got a brilliant age the historical backdrop of Kerala. Key Words; Poorna Swaraj, Jatha, Yuvak Sangh, Agraharam, Ashram Introduction The Indian National Congress becomes a movement of the people. There was a considerable measure of disturbance in the nation when the Simon commission went to India. The general population of India boycotted the commission turn out to be every one of its individuals were British. Despite the noncooperation of the Indians; the commission proceeded with its work and presented the report.