Identification of Taxon Through Fuzzy Classification
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Disaggregation of Bird Families Listed on Cms Appendix Ii
Convention on the Conservation of Migratory Species of Wild Animals 2nd Meeting of the Sessional Committee of the CMS Scientific Council (ScC-SC2) Bonn, Germany, 10 – 14 July 2017 UNEP/CMS/ScC-SC2/Inf.3 DISAGGREGATION OF BIRD FAMILIES LISTED ON CMS APPENDIX II (Prepared by the Appointed Councillors for Birds) Summary: The first meeting of the Sessional Committee of the Scientific Council identified the adoption of a new standard reference for avian taxonomy as an opportunity to disaggregate the higher-level taxa listed on Appendix II and to identify those that are considered to be migratory species and that have an unfavourable conservation status. The current paper presents an initial analysis of the higher-level disaggregation using the Handbook of the Birds of the World/BirdLife International Illustrated Checklist of the Birds of the World Volumes 1 and 2 taxonomy, and identifies the challenges in completing the analysis to identify all of the migratory species and the corresponding Range States. The document has been prepared by the COP Appointed Scientific Councilors for Birds. This is a supplementary paper to COP document UNEP/CMS/COP12/Doc.25.3 on Taxonomy and Nomenclature UNEP/CMS/ScC-Sc2/Inf.3 DISAGGREGATION OF BIRD FAMILIES LISTED ON CMS APPENDIX II 1. Through Resolution 11.19, the Conference of Parties adopted as the standard reference for bird taxonomy and nomenclature for Non-Passerine species the Handbook of the Birds of the World/BirdLife International Illustrated Checklist of the Birds of the World, Volume 1: Non-Passerines, by Josep del Hoyo and Nigel J. Collar (2014); 2. -

Dieter Thomas Tietze Editor How They Arise, Modify and Vanish
Fascinating Life Sciences Dieter Thomas Tietze Editor Bird Species How They Arise, Modify and Vanish Fascinating Life Sciences This interdisciplinary series brings together the most essential and captivating topics in the life sciences. They range from the plant sciences to zoology, from the microbiome to macrobiome, and from basic biology to biotechnology. The series not only highlights fascinating research; it also discusses major challenges associated with the life sciences and related disciplines and outlines future research directions. Individual volumes provide in-depth information, are richly illustrated with photographs, illustrations, and maps, and feature suggestions for further reading or glossaries where appropriate. Interested researchers in all areas of the life sciences, as well as biology enthusiasts, will find the series’ interdisciplinary focus and highly readable volumes especially appealing. More information about this series at http://www.springer.com/series/15408 Dieter Thomas Tietze Editor Bird Species How They Arise, Modify and Vanish Editor Dieter Thomas Tietze Natural History Museum Basel Basel, Switzerland ISSN 2509-6745 ISSN 2509-6753 (electronic) Fascinating Life Sciences ISBN 978-3-319-91688-0 ISBN 978-3-319-91689-7 (eBook) https://doi.org/10.1007/978-3-319-91689-7 Library of Congress Control Number: 2018948152 © The Editor(s) (if applicable) and The Author(s) 2018. This book is an open access publication. Open Access This book is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made. -

FIRST OCCURRENCE of the PADDYFIELD WARBLER ACROCEPHALUS AGRICOLA in the Society: Valletta, ,'!Alta
IL-MERILL No. 25 1988 IL-MERILL No. 25 1988 Sultana,J. & Gauci,C. 1982. A New Guide to the Birds of Malta. lhe Ornithological FIRST OCCURRENCE OF THE PADDYFIELD WARBLER ACROCEPHALUS AGRICOLA IN THE Society: Valletta, ,'!alta. MALTESE ISLANDS Sultana,J., Gauci,C. & Beaman M. 1975. A Guide to the Birds of Malta, Malta While ringing in a maize-field at Lunzjata, Gozo on 5 September 1986, an unfamiliar Ornithological Society: Valletta, Malta. Acxocephalus warbler was found in one of the mist-nets. lhe bird's upperparts were similar to those of a Reed Warbler Acrocephalus scirpaceus but with a slightly pale rufous rump. It had a conspicuous whitish supercilium which was well marked behind the Nataline Fenech & Saviour Balzan eye. lhe underparts were whitish with a very pale tinge of buff on the throat, breast N.F. - 35 Main Street, Attard, Malta and belly. lhe flanks had a light olive-brown wash. lhe legs were pinkish with yellow soLes, and the iris was olive brown. It was identified as a Paddyfield Warbler S.B. - 6/7 Mdina Road, Naxxar, Malta. Acrocephalus agricola. Biometrics, taken in mm., were: wing- 55; tail- 49 (outer rectrice 42); bill (from skull)- 14.5 (from feathering)- 9.5; and tarsus 21.5. Wing point was 3rd=4th and it had emarginated 3rd and 4th, and slightly on 5th, primaries (counted ascendantlyl. lhe bird was retrapped in the same area the following day. When released it was heard calling 'gish- gish'. FIRST BREEDING RECORDS OF THE MOORHEN GALLINULA CHLOROPUS IN GOZO lhe Paddyfield Warbler breeds in S.Russia and Asia and is vagrant to Europe. -

Thick-Billed Warbler (Iduna Aedon) at Gambell, Alaska: First Record for North America Gary H
NOTES THICK-BILLED WARBLER (IDUNA AEDON) AT GAMBELL, ALASKA: FIRST RECORD FOR NORTH AMERICA GARY H. ROSENBERG, 8101 North Wheatfield Dr., Tucson, Arizona 85741; [email protected] PAUL E. LEHMAN, 11192 Portobelo Dr., San Diego, California 92124; [email protected] AARON J. LANG, 40208 Alpenglow Circle, Homer, Alaska 99603; [email protected] VICTOR AND RUBEN STOLL, 899 Miller Rd., Centerville, Tennessee 37033; [email protected] In the evening on 8 September 2017, in the “far boneyard” at Gambell, St. Law- rence Island, Alaska (63.78° N, 171.74° W), Victor and Ruben Stoll flushed a pas- serine they could not immediately identify. The “boneyards” are large pits excavated by the resident Yupik Natives seeking buried ivory and artifacts, a result of several thousand years of sea-mammal hunting from this island’s Northwest Cape. Working these pits turns the soil, which has resulted in the growth of relatively lush vegetation consisting of two species of Artemisia, known locally as “wormwood.” The combina- tion of lush vegetation (reaching 0.5–1 m in height) and deep depressions that offer protection from the wind is attractive to migrant and vagrant landbirds in the otherwise flat, gravelly landscape. Soon thereafter, we, along with Greg Scyphers, Monte Taylor, and other birders then at Gambell, converged at the far boneyard in search of the bird. It was soon relocated and seen on the ground briefly by Lang, who suggested it was a Thick-billed Warbler (Iduna aedon), a bird he was familiar with from southeastern Asia and a species not previously recorded in Alaska or North America. -

Molecular Phylogeny and Phylogeography of Reed Warblers and Allies (Aves: Acrocephalidae)
Dissertation submitted to the Combined Faculties for the Natural Sciences and for Mathematics of the Ruperto-Carola University of Heidelberg, Germany for the degree of Doctor of Natural Sciences presented by Tayebeh Arbabi Born in Mashhad, Iran Oral examination: 26 June 2014 Molecular Phylogeny and Phylogeography of Reed Warblers and Allies (Aves: Acrocephalidae) Referees: Prof. Dr. Michael Wink Prof. Dr. Marcus Koch i Table of contents Zusammenfassung..................................................................................................................... v Summary .................................................................................................................................. vi Abbreviations ......................................................................................................................... vii Publications ........................................................................................................................... viii 1 Introduction ............................................................................................................................ 1 1.1 General introduction ......................................................................................................... 1 1.1.1 Avian taxonomy ......................................................................................................... 1 1.1.2 Phylogeny and phylogeography ................................................................................. 2 1.1.3 Molecular markers .................................................................................................... -
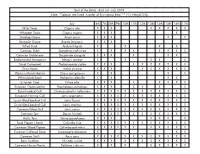
Best of the Baltic - Bird List - July 2019 Note: *Species Are Listed in Order of First Seeing Them ** H = Heard Only
Best of the Baltic - Bird List - July 2019 Note: *Species are listed in order of first seeing them ** H = Heard Only July 6th 7th 8th 9th 10th 11th 12th 13th 14th 15th 16th 17th Mute Swan Cygnus olor X X X X X X X X Whopper Swan Cygnus cygnus X X X X Greylag Goose Anser anser X X X X X Barnacle Goose Branta leucopsis X X X Tufted Duck Aythya fuligula X X X X Common Eider Somateria mollissima X X X X X X X X Common Goldeneye Bucephala clangula X X X X X X Red-breasted Merganser Mergus serrator X X X X X Great Cormorant Phalacrocorax carbo X X X X X X X X X X Grey Heron Ardea cinerea X X X X X X X X X Western Marsh Harrier Circus aeruginosus X X X X White-tailed Eagle Haliaeetus albicilla X X X X Eurasian Coot Fulica atra X X X X X X X X Eurasian Oystercatcher Haematopus ostralegus X X X X X X X Black-headed Gull Chroicocephalus ridibundus X X X X X X X X X X X X European Herring Gull Larus argentatus X X X X X X X X X X X X Lesser Black-backed Gull Larus fuscus X X X X X X X X X X X X Great Black-backed Gull Larus marinus X X X X X X X X X X X X Common/Mew Gull Larus canus X X X X X X X X X X X X Common Tern Sterna hirundo X X X X X X X X X X X X Arctic Tern Sterna paradisaea X X X X X X X Feral Pigeon ( Rock) Columba livia X X X X X X X X X X X X Common Wood Pigeon Columba palumbus X X X X X X X X X X X Eurasian Collared Dove Streptopelia decaocto X X X Common Swift Apus apus X X X X X X X X X X X X Barn Swallow Hirundo rustica X X X X X X X X X X X Common House Martin Delichon urbicum X X X X X X X X White Wagtail Motacilla alba X X -

Egg-Spot Matching in Common Cuckoo Parasitism of the Oriental Reed
Li et al. Avian Res (2016) 7:21 DOI 10.1186/s40657-016-0057-y Avian Research RESEARCH Open Access Egg‑spot matching in common cuckoo parasitism of the oriental reed warbler: effects of host nest availability and egg rejection Donglai Li1†, Yanan Ruan1†, Ying Wang1, Alan K. Chang1, Dongmei Wan1* and Zhengwang Zhang2 Abstract Background: The success of cuckoo parasitism is thought to depend largely on the extent of egg matching between cuckoo and host eggs, since poor-matching cuckoo egg would lead to more frequent egg rejection by the host. In this study, we investigated how egg-spot matching between the Common Cuckoo (Cuculus canorus) and its host, the Oriental Reed Warbler (Acrocephalus orientalis) is affected by the local parasitism rate, nest availability in breeding synchronization and egg rejection. Methods: We used the paired design of parasitized and their nearest non-parasitized nests where breeding occurred simultaneously to compare egg-spot matching. The image analysis was used to compare four eggshell pattern vari- ables, namely spot size, density, coverage on the different areas of egg surface, and the distribution on the whole egg surface. Egg recognition experiments were conducted to test the effect of egg spots on egg rejection by the host. Results: Our results show that much better matching in almost all spot parameters tested on the side of the egg and the spot distribution on the whole egg occurred in parasitized nests than in non-parasitized nests. Matching of spot density between cuckoo and host eggs in parasitized nests increased with the synchronization between temporal availability of nests and the egg-laying period of female cuckoos. -

Songs of the Wild: Temporal and Geographical Distinctions in the Acoustic Properties of the Songs of the Yellow-Breasted Chat
University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln Theses and Dissertations in Animal Science Animal Science Department 12-3-2007 Songs of the Wild: Temporal and Geographical Distinctions in the Acoustic Properties of the Songs of the Yellow-Breasted Chat Jackie L. Canterbury University of Nebraska - Lincoln, [email protected] Follow this and additional works at: https://digitalcommons.unl.edu/animalscidiss Part of the Animal Sciences Commons Canterbury, Jackie L., "Songs of the Wild: Temporal and Geographical Distinctions in the Acoustic Properties of the Songs of the Yellow-Breasted Chat" (2007). Theses and Dissertations in Animal Science. 4. https://digitalcommons.unl.edu/animalscidiss/4 This Article is brought to you for free and open access by the Animal Science Department at DigitalCommons@University of Nebraska - Lincoln. It has been accepted for inclusion in Theses and Dissertations in Animal Science by an authorized administrator of DigitalCommons@University of Nebraska - Lincoln. SONGS OF THE WILD: TEMPORAL AND GEOGRAPHICAL DISTINCTIONS IN THE ACOUSTIC PROPERTIES OF THE SONGS OF THE YELLOW-BREASTED CHAT by Jacqueline Lee Canterbury A DISSERTATION Presented to the Faculty of The Graduate College at the University of Nebraska In Partial Fulfillment of Requirements For the Degree of Doctor of Philosophy Major: Animal Science Under the Supervision of Professors Dr. Mary M. Beck and Dr. Sheila E. Scheideler Lincoln, Nebraska November, 2007 SONGS OF THE WILD: TEMPORAL AND GEOGRAPHICAL DISTINCTIONS IN ACOUSTIC PROPERTIES OF SONG IN THE YELLOW-BREASTED CHAT Jacqueline Lee Canterbury, PhD. University of Nebraska, 2007 Advisors: Mary M. Beck and Sheila E. Scheideler The Yellow-breasted Chat, Icteria virens, is a member of the wood-warbler family, Parulidae, and exists as eastern I. -

Distribution, Ecology, and Life History of the Pearly-Eyed Thrasher (Margarops Fuscatus)
Adaptations of An Avian Supertramp: Distribution, Ecology, and Life History of the Pearly-Eyed Thrasher (Margarops fuscatus) Chapter 6: Survival and Dispersal The pearly-eyed thrasher has a wide geographical distribution, obtains regional and local abundance, and undergoes morphological plasticity on islands, especially at different elevations. It readily adapts to diverse habitats in noncompetitive situations. Its status as an avian supertramp becomes even more evident when one considers its proficiency in dispersing to and colonizing small, often sparsely The pearly-eye is a inhabited islands and disturbed habitats. long-lived species, Although rare in nature, an additional attribute of a supertramp would be a even for a tropical protracted lifetime once colonists become established. The pearly-eye possesses passerine. such an attribute. It is a long-lived species, even for a tropical passerine. This chapter treats adult thrasher survival, longevity, short- and long-range natal dispersal of the young, including the intrinsic and extrinsic characteristics of natal dispersers, and a comparison of the field techniques used in monitoring the spatiotemporal aspects of dispersal, e.g., observations, biotelemetry, and banding. Rounding out the chapter are some of the inherent and ecological factors influencing immature thrashers’ survival and dispersal, e.g., preferred habitat, diet, season, ectoparasites, and the effects of two major hurricanes, which resulted in food shortages following both disturbances. Annual Survival Rates (Rain-Forest Population) In the early 1990s, the tenet that tropical birds survive much longer than their north temperate counterparts, many of which are migratory, came into question (Karr et al. 1990). Whether or not the dogma can survive, however, awaits further empirical evidence from additional studies. -

Diet of Houbara Bustard Chlamydotis Undulata in Punjab, Pakistan
Forktail 20 (2004) SHORT NOTES 91 belly and underwing, with a striking white lower belly. ACKNOWLEDGEMENTS It was clearly an adult. At least one female Great Frigatebird was identified in the group. Several females Fieldwork in East Timor, undertaken on behalf of BirdLife with white spurs on the axillary feathers were also International Asia Programme, was supported by the Asia Bird Fund observed, however I could not determine whether they of BirdLife International, with principal support from The Garfield were Lesser Frigatebird Fregata ariel or Christmas Foundation and the BirdLife Rare Bird Club. Island Frigatebird (possibly both were present). Frigatebirds are regular along the coast near Dili with observations of small numbers every few days in REFERENCES the period March–May 2003. A large group of up to 150 BirdLife International (2001) Threatened birds of Asia: the BirdLife individuals was frequently seen at Manatutu. The only International Red Data Book. Cambridge, U.K.: BirdLife other record of Christmas Island Frigatebird for Timor International. was also of a single adult male, observed along the coast Coates, B. J. and Bishop, K. D. (1997) A guide to the birds of Wallacea. near Kupang on 26 June 1986 (McKean 1987). Alderley, Australia: Dove Publications. The Christmas Island Frigatebird is considered a Johnstone, R. E., van Balen, S., Dekker, R. W. R. J. (1993) New vagrant to the Lesser Sundas (BirdLife International bird records for the island of Lombok. Kukila 6: 124–127. 2001). However it should be emphasised that limited McKean, J. L. (1987). A first record of Christmas Island Frigatebird Fregata andrewsi on Timor. -
![Explorer Research Article [Tripathi Et Al., 6(3): March, 2015:4304-4316] CODEN (USA): IJPLCP ISSN: 0976-7126 INTERNATIONAL JOURNAL of PHARMACY & LIFE SCIENCES (Int](https://docslib.b-cdn.net/cover/4638/explorer-research-article-tripathi-et-al-6-3-march-2015-4304-4316-coden-usa-ijplcp-issn-0976-7126-international-journal-of-pharmacy-life-sciences-int-1074638.webp)
Explorer Research Article [Tripathi Et Al., 6(3): March, 2015:4304-4316] CODEN (USA): IJPLCP ISSN: 0976-7126 INTERNATIONAL JOURNAL of PHARMACY & LIFE SCIENCES (Int
Explorer Research Article [Tripathi et al., 6(3): March, 2015:4304-4316] CODEN (USA): IJPLCP ISSN: 0976-7126 INTERNATIONAL JOURNAL OF PHARMACY & LIFE SCIENCES (Int. J. of Pharm. Life Sci.) Study on Bird Diversity of Chuhiya Forest, District Rewa, Madhya Pradesh, India Praneeta Tripathi1*, Amit Tiwari2, Shivesh Pratap Singh1 and Shirish Agnihotri3 1, Department of Zoology, Govt. P.G. College, Satna, (MP) - India 2, Department of Zoology, Govt. T.R.S. College, Rewa, (MP) - India 3, Research Officer, Fishermen Welfare and Fisheries Development Department, Bhopal, (MP) - India Abstract One hundred and twenty two species of birds belonging to 19 orders, 53 families and 101 genera were recorded at Chuhiya Forest, Rewa, Madhya Pradesh, India from all the three seasons. Out of these as per IUCN red list status 1 species is Critically Endangered, 3 each are Vulnerable and Near Threatened and rest are under Least concern category. Bird species, Gyps bengalensis, which is comes under Falconiformes order and Accipitridae family are critically endangered. The study area provide diverse habitat in the form of dense forest and agricultural land. Rose- ringed Parakeets, Alexandrine Parakeets, Common Babblers, Common Myna, Jungle Myna, Baya Weavers, House Sparrows, Paddyfield Pipit, White-throated Munia, White-bellied Drongo, House crows, Philippine Crows, Paddyfield Warbler etc. were prominent bird species of the study area, which are adapted to diversified habitat of Chuhiya Forest. Human impacts such as Installation of industrial units, cutting of trees, use of insecticides in agricultural practices are major threats to bird communities. Key-Words: Bird, Chuhiya Forest, IUCN, Endangered Introduction Birds (class-Aves) are feathered, winged, two-legged, Birds are ideal bio-indicators and useful models for warm-blooded, egg-laying vertebrates. -

A New Subspecies of Eurasian Reed Warbler Acrocephalus Scirpaceus in Egypt
Jens Hering et al. 101 Bull. B.O.C. 2016 136(2) A new subspecies of Eurasian Reed Warbler Acrocephalus scirpaceus in Egypt by Jens Hering, Hans Winkler & Frank D. Steinheimer Received 4 December 2015 Summary.—A new subspecies of European Reed Warbler Acrocephalus scirpaceus is described from the Egypt / Libya border region in the northern Sahara. Intensive studies revealed the new form to be clearly diagnosable within the Eurasian / African Reed Warbler superspecies, especially in biometrics, habitat, breeding biology and behaviour. The range of this sedentary form lies entirely below sea level, in the large depressions of the eastern Libyan Desert, in Qattara, Siwa, Sitra and Al Jaghbub. The most important field characters are the short wings and tarsi, which are significantly different from closely related A. s. scirpaceus, A. s. fuscus and A. s. avicenniae, less so from A. baeticatus cinnamomeus, which is more clearly separated by behaviour / nest sites and toe length. Molecular genetic analyses determined that uncorrected distances to A. s. scirpaceus are 1.0–1.3%, to avicenniae 1.1–1.5% and to fuscus 0.3–1.2%. The song is similar to that of other Eurasian Reed Warbler taxa as well as that of African Reed Warbler A. baeticatus, but the succession of individual elements appears slower than in A. s. scirpaceus and therefore shows more resemblance to A. s. avicenniae. Among the new subspecies’ unique traits are that its preferred breeding habitat in the Siwa Oasis complex, besides stands of reed, is date palms and olive trees. A breeding density of 107 territories per 10 ha was recorded in the cultivated area.