Mercury's Resonant Rotation from Secular Orbital Elements
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
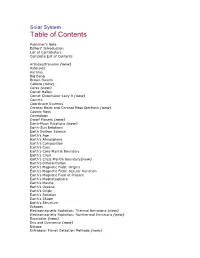
Table of Contents
Solar System Table of Contents Publisher's Note Editors' Introduction List of Contributors Complete List of Contents Archeaostronomy (new) Asteroids Auroras Big Bang Brown Dwarfs Callisto (new) Ceres (new) Comet Halley Comet Shoemaker-Levy 9 (new) Comets Coordinate Systems Coronal Holes and Coronal Mass Ejections (new) Cosmic Rays Cosmology Dwarf Planets (new) Earth-Moon Relations (new) Earth-Sun Relations Earth System Science Earth's Age Earth's Atmosphere Earth's Composition Earth's Core Earth's Core-Mantle Boundary Earth's Crust Earth's Crust-Mantle Boundary(new) Earth's Differentiation Earth's Magnetic Field: Origins Earth's Magnetic Field: Secular Variation Earth's Magnetic Field at Present Earth's Magnetosphere Earth's Mantle Earth's Oceans Earth's Origin Earth's Rotation Earth's Shape Earth's Structure Eclipses Electromagnetic Radiation: Thermal Emissions (new) Electromagnetic Radiation: Nonthermal Emissions (new) Enceladus (new) Eris and Dysnomia (new) Europa Extrasolar Planet Detection Methods (new) Extrasolar Planetary Systems Extraterrestrial Life in the Solar System Gamma-Ray Bursters Ganymede (new) General Relativity Gravity Measurement Greenhouse Effect Habitable Zones (new) Hertzsprung-Russell Diagram Iapetus (new) Impact Cratering Infrared Astronomy Interstellar Clouds and the Interstellar Medium Interplanetary Environment (new) Io Jovian Planets Jupiter's Atmosphere Jupiter's Great Red Spot Jupiter's Interior (new) Jupiter's Magnetic Field and Radiation Belts Jupiter's Ring System (new) Jupiter's Satellites Kuiper Belt -

Astrodynamics
Politecnico di Torino SEEDS SpacE Exploration and Development Systems Astrodynamics II Edition 2006 - 07 - Ver. 2.0.1 Author: Guido Colasurdo Dipartimento di Energetica Teacher: Giulio Avanzini Dipartimento di Ingegneria Aeronautica e Spaziale e-mail: [email protected] Contents 1 Two–Body Orbital Mechanics 1 1.1 BirthofAstrodynamics: Kepler’sLaws. ......... 1 1.2 Newton’sLawsofMotion ............................ ... 2 1.3 Newton’s Law of Universal Gravitation . ......... 3 1.4 The n–BodyProblem ................................. 4 1.5 Equation of Motion in the Two-Body Problem . ....... 5 1.6 PotentialEnergy ................................. ... 6 1.7 ConstantsoftheMotion . .. .. .. .. .. .. .. .. .... 7 1.8 TrajectoryEquation .............................. .... 8 1.9 ConicSections ................................... 8 1.10 Relating Energy and Semi-major Axis . ........ 9 2 Two-Dimensional Analysis of Motion 11 2.1 ReferenceFrames................................. 11 2.2 Velocity and acceleration components . ......... 12 2.3 First-Order Scalar Equations of Motion . ......... 12 2.4 PerifocalReferenceFrame . ...... 13 2.5 FlightPathAngle ................................. 14 2.6 EllipticalOrbits................................ ..... 15 2.6.1 Geometry of an Elliptical Orbit . ..... 15 2.6.2 Period of an Elliptical Orbit . ..... 16 2.7 Time–of–Flight on the Elliptical Orbit . .......... 16 2.8 Extensiontohyperbolaandparabola. ........ 18 2.9 Circular and Escape Velocity, Hyperbolic Excess Speed . .............. 18 2.10 CosmicVelocities -

Flight and Orbital Mechanics
Flight and Orbital Mechanics Lecture slides Challenge the future 1 Flight and Orbital Mechanics AE2-104, lecture hours 21-24: Interplanetary flight Ron Noomen October 25, 2012 AE2104 Flight and Orbital Mechanics 1 | Example: Galileo VEEGA trajectory Questions: • what is the purpose of this mission? • what propulsion technique(s) are used? • why this Venus- Earth-Earth sequence? • …. [NASA, 2010] AE2104 Flight and Orbital Mechanics 2 | Overview • Solar System • Hohmann transfer orbits • Synodic period • Launch, arrival dates • Fast transfer orbits • Round trip travel times • Gravity Assists AE2104 Flight and Orbital Mechanics 3 | Learning goals The student should be able to: • describe and explain the concept of an interplanetary transfer, including that of patched conics; • compute the main parameters of a Hohmann transfer between arbitrary planets (including the required ΔV); • compute the main parameters of a fast transfer between arbitrary planets (including the required ΔV); • derive the equation for the synodic period of an arbitrary pair of planets, and compute its numerical value; • derive the equations for launch and arrival epochs, for a Hohmann transfer between arbitrary planets; • derive the equations for the length of the main mission phases of a round trip mission, using Hohmann transfers; and • describe the mechanics of a Gravity Assist, and compute the changes in velocity and energy. Lecture material: • these slides (incl. footnotes) AE2104 Flight and Orbital Mechanics 4 | Introduction The Solar System (not to scale): [Aerospace -

Habitability of Planets on Eccentric Orbits: Limits of the Mean Flux Approximation
A&A 591, A106 (2016) Astronomy DOI: 10.1051/0004-6361/201628073 & c ESO 2016 Astrophysics Habitability of planets on eccentric orbits: Limits of the mean flux approximation Emeline Bolmont1, Anne-Sophie Libert1, Jeremy Leconte2; 3; 4, and Franck Selsis5; 6 1 NaXys, Department of Mathematics, University of Namur, 8 Rempart de la Vierge, 5000 Namur, Belgium e-mail: [email protected] 2 Canadian Institute for Theoretical Astrophysics, 60st St George Street, University of Toronto, Toronto, ON, M5S3H8, Canada 3 Banting Fellow 4 Center for Planetary Sciences, Department of Physical & Environmental Sciences, University of Toronto Scarborough, Toronto, ON, M1C 1A4, Canada 5 Univ. Bordeaux, LAB, UMR 5804, 33270 Floirac, France 6 CNRS, LAB, UMR 5804, 33270 Floirac, France Received 4 January 2016 / Accepted 28 April 2016 ABSTRACT Unlike the Earth, which has a small orbital eccentricity, some exoplanets discovered in the insolation habitable zone (HZ) have high orbital eccentricities (e.g., up to an eccentricity of ∼0.97 for HD 20782 b). This raises the question of whether these planets have surface conditions favorable to liquid water. In order to assess the habitability of an eccentric planet, the mean flux approximation is often used. It states that a planet on an eccentric orbit is called habitable if it receives on average a flux compatible with the presence of surface liquid water. However, because the planets experience important insolation variations over one orbit and even spend some time outside the HZ for high eccentricities, the question of their habitability might not be as straightforward. We performed a set of simulations using the global climate model LMDZ to explore the limits of the mean flux approximation when varying the luminosity of the host star and the eccentricity of the planet. -

Four Centuries of Geomagnetic Secular Variation from Historical Records
Fourcenturies of geomagnetic secular variationfrom historical records ByAndrewJackson 1,ArtR.T. Jonkers 2 andMatthewR.W alker 1 1School ofEarth Sciences, Leeds University,Leeds LS29JT, UK 2Departmentof History, V rijeUniversiteit, Amsterdam, The Netherlands Wepresent anewmodel of the magnetic eld at the core{mantle boundary for the interval 1590{1990. Themodel, called gufm1,is based on amassive newcompilation of historical observations of the magnetic eld. The greater part of the newdataset originates from unpublished observations taken by mariners engaged in merchant and naval shipping. Considerable attention is given to both correction of data for possible mislocation (originating from poor knowledge of longitude) and to proper allocation of error in the data. Weadopt astochastic model for uncorrected positional errors that properly accounts for the nature of the noise process based on aBrownian motion model. Thevariability of navigational errors as afunction of the duration of the voyages that wehave analysed isconsistent with this model. For the period before 1800, more than 83 000 individual observations of magnetic declination wererecorded at more than 64 000 locations; more than 8000 new observations are for the 17th century alone. Thetime-dependent eld model that weconstruct from the dataset is parametrized spatially in terms of spherical harmonics and temporally in B-splines, using atotal of 36 512 parameters. Themodel has improved the resolution of the core eld, and represents the longest continuous model of the eld available. However, full exploitation of the database may demand anew modelling methodology. Keywords: Earth’score; geom agneticsec ularvariation ; magnetic¯ eld;m aritimehistory 1.Intro duction TheEarth has possessed amagnetic eld for more than 4billion years, generated in the ®uid core. -

Effects of Planetesimals' Random Velocity on Tempo
42nd Lunar and Planetary Science Conference (2011) 1154.pdf EFFECTS OF PLANETESIMALS’ RANDOM VELOCITY ON TEMPO- RARY CAPTURE BY A PLANET Ryo Suetsugu1, Keiji Ohtsuki1;2;3, Takayuki Tanigawa2;4. 1Department of Earth and Planetary Sciences, Kobe University, Kobe 657-8501, Japan; 2Center for Planetary Science, Kobe University, Kobe 657-8501, Japan; 3Laboratory for Atmospheric and Space Physics, University of Colorado, Boulder, CO 80309-0392; 4Institute of Low Temperature Science, Hokkaido University, Sapporo 060-0819, Japan Introduction: When planetesimals encounter with a of large orbital eccentricities were not examined in detail. planet, the typical duration of close encounter during Moreover, the above calculations assumed that planetesi- which they pass within or near the planet’s Hill sphere is mals and a planet were initially in the same orbital plane, smaller than or comparable to the planet’s orbital period. and effects of orbital inclination were not studied. However, in some cases, planetesimals are captured by In the present work, we examine temporary capture the planet’s gravity and orbit about the planet for an ex- of planetesimals initially on eccentric and inclined orbits tended period of time, before they escape from the vicin- about the Sun. ity of the planet. This phenomenon is called temporary capture. Temporary capture may play an important role Numerical Method: We examine temporary capture us- in the origin and dynamical evolution of various kinds of ing three-body orbital integration (i.e. the Sun, a planet, a small bodies in the Solar System, such as short-period planetesimal). When the masses of planetesimals and the comets and irregular satellites. -

Perturbation Theory in Celestial Mechanics
Perturbation Theory in Celestial Mechanics Alessandra Celletti Dipartimento di Matematica Universit`adi Roma Tor Vergata Via della Ricerca Scientifica 1, I-00133 Roma (Italy) ([email protected]) December 8, 2007 Contents 1 Glossary 2 2 Definition 2 3 Introduction 2 4 Classical perturbation theory 4 4.1 The classical theory . 4 4.2 The precession of the perihelion of Mercury . 6 4.2.1 Delaunay action–angle variables . 6 4.2.2 The restricted, planar, circular, three–body problem . 7 4.2.3 Expansion of the perturbing function . 7 4.2.4 Computation of the precession of the perihelion . 8 5 Resonant perturbation theory 9 5.1 The resonant theory . 9 5.2 Three–body resonance . 10 5.3 Degenerate perturbation theory . 11 5.4 The precession of the equinoxes . 12 6 Invariant tori 14 6.1 Invariant KAM surfaces . 14 6.2 Rotational tori for the spin–orbit problem . 15 6.3 Librational tori for the spin–orbit problem . 16 6.4 Rotational tori for the restricted three–body problem . 17 6.5 Planetary problem . 18 7 Periodic orbits 18 7.1 Construction of periodic orbits . 18 7.2 The libration in longitude of the Moon . 20 1 8 Future directions 20 9 Bibliography 21 9.1 Books and Reviews . 21 9.2 Primary Literature . 22 1 Glossary KAM theory: it provides the persistence of quasi–periodic motions under a small perturbation of an integrable system. KAM theory can be applied under quite general assumptions, i.e. a non– degeneracy of the integrable system and a diophantine condition of the frequency of motion. -

Session 6:Analytical Approximations for Low Thrust Maneuvers
Session 6: Analytical Approximations for Low Thrust Maneuvers As mentioned in the previous lecture, solving non-Keplerian problems in general requires the use of perturbation methods and many are only solvable through numerical integration. However, there are a few examples of low-thrust space propulsion maneuvers for which we can find approximate analytical expressions. In this lecture, we explore a couple of these maneuvers, both of which are useful because of their precision and practical value: i) climb or descent from a circular orbit with continuous thrust, and ii) in-orbit repositioning, or walking. Spiral Climb/Descent We start by writing the equations of motion in polar coordinates, 2 d2r �dθ � µ − r + = a (1) 2 2 r dt dt r 2 d θ 2 dr dθ aθ + = (2) 2 dt r dt dt r We assume continuous thrust in the angular direction, therefore ar = 0. If the acceleration force along θ is small, then we can safely assume the orbit will remain nearly circular and the semi-major axis will be just slightly different after one orbital period. Of course, small and slightly are vague words. To make the analysis rigorous, we need to be more precise. Let us say that for this approximation to be valid, the angular acceleration has to be much smaller than the corresponding centrifugal or gravitational forces (the last two terms in the LHS of Eq. (1)) and that the radial acceleration (the first term in the LHS in the same equation) is negligible. Given these assumptions, from Eq. (1), dθ r µ d2θ 3 r µ dr ≈ ! ≈ − (3) 3 2 5 dt r dt 2 r dt Substituting into Eq. -

Jupitor's Great Red Spot
GREAT RED SPOT appears somewhat orange in this remarkably ly ranged from '.'full gray" and "pinkish" to "brick red" and "car· detailed photograph made at the Lunar and Planetary Laboratory mine." The photograph was made on December 23, 1966, by Alika of the University of Arizona. During the century or so that Jupiter's Herring and John Fountain, who used a 61·inch reflecting tele· great red spot bas been closely observed its color has reported. scope. The exposure was one second on High Speed Ektachrome. © 1968 SCIENTIFIC AMERICAN, INC JUPITER'S GREAT RED SPOT There is evidence to suggest that this peculiar Inarking is the top of a "Taylor cohunn": a stagnant region above a bll111p 01' depression at the botton1 of a circulating fluid by Haymond Hide he surface markings of the plan To explain the fluctuations in the red tals suspended in an atmosphere that is Tets have always had a special fas spot's period of rotation one must assume mainly hydrogen admixed with water cination, and no single marking that there are forces acting on the solid and perhaps methane and helium. Other has been more fascinating and puzzling planet capable of causing an equivalent lines of evidence, particularly the fact than the great red spot of Jupiter. Un change in its rotation period. In other that Jupiter's density is only 1.3 times like the elusive "canals" of Mars, the red words, the fluctuations in the rotation the density of water, suggest that the spot unmistakably exists. Although it has period of the red spot are to be regarded main constituents of the planet are hy been known to fade and change color, it as a true reflection of the rotation period drogen and helium. -

New Closed-Form Solutions for Optimal Impulsive Control of Spacecraft Relative Motion
New Closed-Form Solutions for Optimal Impulsive Control of Spacecraft Relative Motion Michelle Chernick∗ and Simone D'Amicoy Aeronautics and Astronautics, Stanford University, Stanford, California, 94305, USA This paper addresses the fuel-optimal guidance and control of the relative motion for formation-flying and rendezvous using impulsive maneuvers. To meet the requirements of future multi-satellite missions, closed-form solutions of the inverse relative dynamics are sought in arbitrary orbits. Time constraints dictated by mission operations and relevant perturbations acting on the formation are taken into account by splitting the optimal recon- figuration in a guidance (long-term) and control (short-term) layer. Both problems are cast in relative orbit element space which allows the simple inclusion of secular and long-periodic perturbations through a state transition matrix and the translation of the fuel-optimal optimization into a minimum-length path-planning problem. Due to the proper choice of state variables, both guidance and control problems can be solved (semi-)analytically leading to optimal, predictable maneuvering schemes for simple on-board implementation. Besides generalizing previous work, this paper finds four new in-plane and out-of-plane (semi-)analytical solutions to the optimal control problem in the cases of unperturbed ec- centric and perturbed near-circular orbits. A general delta-v lower bound is formulated which provides insight into the optimality of the control solutions, and a strong analogy between elliptic Hohmann transfers and formation-flying control is established. Finally, the functionality, performance, and benefits of the new impulsive maneuvering schemes are rigorously assessed through numerical integration of the equations of motion and a systematic comparison with primer vector optimal control. -

Coordinate Systems in Geodesy
COORDINATE SYSTEMS IN GEODESY E. J. KRAKIWSKY D. E. WELLS May 1971 TECHNICALLECTURE NOTES REPORT NO.NO. 21716 COORDINATE SYSTElVIS IN GEODESY E.J. Krakiwsky D.E. \Vells Department of Geodesy and Geomatics Engineering University of New Brunswick P.O. Box 4400 Fredericton, N .B. Canada E3B 5A3 May 1971 Latest Reprinting January 1998 PREFACE In order to make our extensive series of lecture notes more readily available, we have scanned the old master copies and produced electronic versions in Portable Document Format. The quality of the images varies depending on the quality of the originals. The images have not been converted to searchable text. TABLE OF CONTENTS page LIST OF ILLUSTRATIONS iv LIST OF TABLES . vi l. INTRODUCTION l 1.1 Poles~ Planes and -~es 4 1.2 Universal and Sidereal Time 6 1.3 Coordinate Systems in Geodesy . 7 2. TERRESTRIAL COORDINATE SYSTEMS 9 2.1 Terrestrial Geocentric Systems • . 9 2.1.1 Polar Motion and Irregular Rotation of the Earth • . • • . • • • • . 10 2.1.2 Average and Instantaneous Terrestrial Systems • 12 2.1. 3 Geodetic Systems • • • • • • • • • • . 1 17 2.2 Relationship between Cartesian and Curvilinear Coordinates • • • • • • • . • • 19 2.2.1 Cartesian and Curvilinear Coordinates of a Point on the Reference Ellipsoid • • • • • 19 2.2.2 The Position Vector in Terms of the Geodetic Latitude • • • • • • • • • • • • • • • • • • • 22 2.2.3 Th~ Position Vector in Terms of the Geocentric and Reduced Latitudes . • • • • • • • • • • • 27 2.2.4 Relationships between Geodetic, Geocentric and Reduced Latitudes • . • • • • • • • • • • 28 2.2.5 The Position Vector of a Point Above the Reference Ellipsoid . • • . • • • • • • . .• 28 2.2.6 Transformation from Average Terrestrial Cartesian to Geodetic Coordinates • 31 2.3 Geodetic Datums 33 2.3.1 Datum Position Parameters . -

SPITZER SPACE TELESCOPE MID-IR LIGHT CURVES of NEPTUNE John Stauffer1, Mark S
The Astronomical Journal, 152:142 (8pp), 2016 November doi:10.3847/0004-6256/152/5/142 © 2016. The American Astronomical Society. All rights reserved. SPITZER SPACE TELESCOPE MID-IR LIGHT CURVES OF NEPTUNE John Stauffer1, Mark S. Marley2, John E. Gizis3, Luisa Rebull1,4, Sean J. Carey1, Jessica Krick1, James G. Ingalls1, Patrick Lowrance1, William Glaccum1, J. Davy Kirkpatrick5, Amy A. Simon6, and Michael H. Wong7 1 Spitzer Science Center (SSC), California Institute of Technology, Pasadena, CA 91125, USA 2 NASA Ames Research Center, Space Sciences and Astrobiology Division, MS245-3, Moffett Field, CA 94035, USA 3 Department of Physics and Astronomy, University of Delaware, Newark, DE 19716, USA 4 Infrared Science Archive (IRSA), 1200 E. California Boulevard, MS 314-6, California Institute of Technology, Pasadena, CA 91125, USA 5 Infrared Processing and Analysis Center, MS 100-22, California Institute of Technology, Pasadena, CA 91125, USA 6 NASA Goddard Space Flight Center, Solar System Exploration Division (690.0), 8800 Greenbelt Road, Greenbelt, MD 20771, USA 7 University of California, Department of Astronomy, Berkeley CA 94720-3411, USA Received 2016 July 13; revised 2016 August 12; accepted 2016 August 15; published 2016 October 27 ABSTRACT We have used the Spitzer Space Telescope in 2016 February to obtain high cadence, high signal-to-noise, 17 hr duration light curves of Neptune at 3.6 and 4.5 μm. The light curve duration was chosen to correspond to the rotation period of Neptune. Both light curves are slowly varying with time, with full amplitudes of 1.1 mag at 3.6 μm and 0.6 mag at 4.5 μm.