A Search for Champion Boxers
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Mike Tyson Brings His Undisputed: Round 2 Tour to Four Winds New Buffalo’S Silver Creek Event Center on Friday, July 10
FOR IMMEDIATE RELEASE MIKE TYSON BRINGS HIS UNDISPUTED: ROUND 2 TOUR TO FOUR WINDS NEW BUFFALO’S SILVER CREEK EVENT CENTER ON FRIDAY, JULY 10 Tickets go on sale on Friday, April 10 NEW BUFFALO, Mich. – April 8, 2020 – The Pokagon Band of Potawatomi’s Four Winds® Casinos are pleased to announce that Mike Tyson will bring his Undisputed Truth: Round 2 tour to Four Winds New Buffalo’s Silver Creek® Event Center on Friday, July 10, at 9 p.m. The one-man show features the world’s most illustrious heavyweight boxing champion, who returns to the stage with real life untold stories, focusing on the ups and downs of his tumultuous and ultimately triumphant, post-boxing life and career. In an up-close-and-personal setting featuring images and videos, Tyson delivers captivating vignettes from his life, experiences as a professional athlete and controversies in between. It’s truly raw and electric theater, in its purest form. Ticket prices for the show range from $55 to $85, plus applicable fees, and can be purchased online at www.fourwindscasino.com beginning on Friday, April 10 at 10 a.m. Eastern. Mike Tyson is a larger-than-life legend – both in and out of the ring. Tenacious, talented, and thrilling to watch, Tyson embodies the grit and electrifying excitement of the sport. With nicknames such as Iron Mike, Kid Dynamite, and The Baddest Man on the Planet, it’s no surprise that Tyson’s legacy is the stuff of a legend. Tyson was one of the most feared boxers in the ring, and one look at his resume proves he is one of boxing’s greats. -

Recapturing Our Identity Through Arts and Crafts" Event to Make Sure That Doesn't Occur
Rez Car Show Teaching Hammock Youth Conference “Looking Back at the Seminole Trail” Page 3 Page 13 Page 14 Presort Standard U.S. Postage Paid S. Florida, FL Permit No. 1624 “Voice of the Unconquered” 50¢ www.seminoletribe.com Volume XXIV • Number 11 August 15, 2003 2003-2004 Seminole Princesses Hollywood Youth Conference Visits Historical Sites “Looking Back at the Seminole Trail” ORLANDO — Members of the Hollywood Youth Conference journeyed back in time, visiting the historic grounds of Fort King, Castillo de San Marcos, and the infamous Dade Battlefield. "Looking Back at the Seminole Trail" offered Seminoles a look into their distinguished past. From July 7 through 11, Children and adults learned about the brave warriors who refused to relin- quish their land, their homes, and their way of life. The Seminoles fought back against the U.S. Army and never signed a treaty, which is why the Seminoles are known as "The Unconquered." On Tuesday July 8, Chairman Mitchell Cypress, President Moses B. Osceola, Hollywood Council Representative Max B. Osceola, and Michael Kelly Hollywood Board Representative David DeHass Dan Osceola prefers using cypress wood for his carvings. spoke to everyone in attendance. They stressed the importance of the Youth Conference and wanted each and everyone to get something out of it. "As a youth, we didn't get much of a chance to see all these historic sites. We only read about Recapturing Our them. You all have the opportunity to see history," said Mitchell Cypress. Moses Osceola stated, "The staff has planned Identity Through some great things for you this week. -

Dec 2004 Current List
Fighter Opponent Result / RoundsUnless specifiedDate fights / Time are not ESPN NetworkClassic, Superbouts. Comments Ali Al "Blue" Lewis TKO 11 Superbouts Ali fights his old sparring partner Ali Alfredo Evangelista W 15 Post-fight footage - Ali not in great shape Ali Archie Moore TKO 4 10 min Classic Sports Hi-Lites Only Ali Bob Foster KO 8 21-Nov-1972 ABC Commentary by Cossell - Some break up in picture Ali Bob Foster KO 8 21-Nov-1972 British CC Ali gets cut Ali Brian London TKO 3 B&W Ali in his prime Ali Buster Mathis W 12 Commentary by Cossell - post-fight footage Ali Chuck Wepner KO 15 Classic Sports Ali Cleveland Williams TKO 3 14-Nov-1966 B&W Commentary by Don Dunphy - Ali in his prime Ali Cleveland Williams TKO 3 14-Nov-1966 Classic Sports Ali in his prime Ali Doug Jones W 10 Jones knows how to fight - a tough test for Cassius Ali Earnie Shavers W 15 Brutal battle - Shavers rocks Ali with right hand bombs Ali Ernie Terrell W 15 Feb, 1967 Classic Sports Commentary by Cossell Ali Floyd Patterson i TKO 12 22-Nov-1965 B&W Ali tortures Floyd Ali Floyd Patterson ii TKO 7 Superbouts Commentary by Cossell Ali George Chuvalo i W 15 Classic Sports Ali has his hands full with legendary tough Canadian Ali George Chuvalo ii W 12 Superbouts In shape Ali battles in shape Chuvalo Ali George Foreman KO 8 Pre- & post-fight footage Ali Gorilla Monsoon Wrestling Ali having fun Ali Henry Cooper i TKO 5 Classic Sports Hi-Lites Only Ali Henry Cooper ii TKO 6 Classic Sports Hi-Lites Only - extensive pre-fight Ali Ingemar Johansson Sparring 5 min B&W Silent audio - Sparring footage Ali Jean Pierre Coopman KO 5 Rumor has it happy Pierre drank before the bout Ali Jerry Quarry ii TKO 7 British CC Pre- & post-fight footage Ali Jerry Quarry ii TKO 7 Superbouts Ali at his relaxed best Ali Jerry Quarry i TKO 3 Ali cuts up Quarry Ali Jerry Quarry ii TKO 7 British CC Pre- & post-fight footage Ali Jimmy Ellis TKO 12 Ali beats his old friend and sparring partner Ali Jimmy Young W 15 Ali is out of shape and gets a surprise from Young Ali Joe Bugner i W 12 Incomplete - Missing Rds. -

ANNUAL UCLA FOOTBALL AWARDS Henry R
2005 UCLA FOOTBALL MEDIA GUIDE NON-PUBLISHED SUPPLEMENT UCLA CAREER LEADERS RUSHING PASSING Years TCB TYG YL NYG Avg Years Att Comp TD Yds Pct 1. Gaston Green 1984-87 708 3,884 153 3,731 5.27 1. Cade McNown 1995-98 1,250 694 68 10,708 .555 2. Freeman McNeil 1977-80 605 3,297 102 3,195 5.28 2. Tom Ramsey 1979-82 751 441 50 6,168 .587 3. DeShaun Foster 1998-01 722 3,454 260 3,194 4.42 3. Cory Paus 1999-02 816 439 42 6,877 .538 4. Karim Abdul-Jabbar 1992-95 608 3,341 159 3,182 5.23 4. Drew Olson 2002- 770 422 33 5,334 .548 5. Wendell Tyler 1973-76 526 3,240 59 3,181 6.04 5. Troy Aikman 1987-88 627 406 41 5,298 .648 6. Skip Hicks 1993-94, 96-97 638 3,373 233 3,140 4.92 6. Tommy Maddox 1990-91 670 391 33 5,363 .584 7. Theotis Brown 1976-78 526 2,954 40 2,914 5.54 7. Wayne Cook 1991-94 612 352 34 4,723 .575 8. Kevin Nelson 1980-83 574 2,687 104 2,583 4.50 8. Dennis Dummit 1969-70 552 289 29 4,356 .524 9. Kermit Johnson 1971-73 370 2,551 56 2,495 6.74 9. Gary Beban 1965-67 465 243 23 4,087 .522 10. Kevin Williams 1989-92 418 2,348 133 2,215 5.30 10. Matt Stevens 1983-86 431 231 16 2,931 .536 11. -

Behind the Mask: My Autobiography
Contents 1. List of Illustrations 2. Prologue 3. Introduction 4. 1 King for a Day 5. 2 Destiny’s Child 6. 3 Paris 7. 4 Vested Interests 8. 5 School of Hard Knocks 9. 6 Rolling with the Punches 10. 7 Finding Klitschko 11. 8 The Dark 12. 9 Into the Light 13. 10 Fat Chance 14. 11 Wild Ambition 15. 12 Drawing Power 16. 13 Family Values 17. 14 A New Dawn 18. 15 Bigger than Boxing 19. Illustrations 20. Useful Mental Health Contacts 21. Professional Boxing Record 22. Index About the Author Tyson Fury is the undefeated lineal heavyweight champion of the world. Born and raised in Manchester, Fury weighed just 1lb at birth after being born three months premature. His father John named him after Mike Tyson. From Irish traveller heritage, the“Gypsy King” is undefeated in 28 professional fights, winning 27 with 19 knockouts, and drawing once. His most famous victory came in 2015, when he stunned longtime champion Wladimir Klitschko to win the WBA, IBF and WBO world heavyweight titles. He was forced to vacate the belts because of issues with drugs, alcohol and mental health, and did not fight again for more than two years. Most thought he was done with boxing forever. Until an amazing comeback fight with Deontay Wilder in December 2018. It was an instant classic, ending in a split decision tie. Outside of the ring, Tyson Fury is a mental health ambassador. He donated his million dollar purse from the Deontay Wilder fight to the homeless. This book is dedicated to the cause of mental health awareness. -

World Boxing Association Gilberto Mendoza President Official Ratings As of February 2000
WORLD BOXING ASSOCIATION GILBERTO MENDOZA PRESIDENT OFFICIAL RATINGS AS OF FEBRUARY 2000 CHAIRMAN GILBERTO MENDOZA FAX: (58-44) 633177 P.O. BOX 377 MARACAY 2101-A VICE CHAIRMAN MEMBERS EDO. ARAGUA - VENEZUELA JORGE H. KLEE FAX: (57-3) 58-0621 PHONE:(44) 63-1584 STANLEY CHRISTODOLOU CBA (SOUTH AFRICA) 63-3347 JOSE EMILIO GRAGLIA FEDELATIN (ARGENTINA) FAX: (44) 63-3177 ANIBAL MIRAMONTES NABA (USA) 63-8576 ALAN KIM PABA (KOREA) E-mail: [email protected] SHIGERU KOJIMA JBC (JAPAN) http://www.wbaonline.com/ HEAVYWEIGHT (Over 190 Lbs / Over 86.18 Kgs) CRUISERWEIGHT (190 Lbs / 86.18 Kgs) LIGHT HEAVYWEIGHT (175 Lbs / 79.38 Kgs) World Champion: LENNOX LEWIS G.B World Champion: FABRICE TIOZZO FRA World Champion: ROY JONES USA Won Title: 11-13-99 Won Title: 11-08-97 Won Title: 07-18- 98 Last Mandatory: Last Mandatory: 11-14-98 Last Mandatory: Last Defense: Last Defense: 11-13-99 Last Defense: 01-15-2000 WBC: LENNOX LEWIS - IBF: LENNOX LEWIS WBC: JUAN C. GOMEZ - IBF: VASILI JIROV WBC ROY JONES - IBF: ROY JONES WBO: VITALI KLITSCHKO WBO: JOHNNY NELSON WBO: DARIUSZ MICHALCZEWSKY 1. JOHN RUIZ (WBANA) USA 1. VIRGIL HILL USA 1. RICHARD HALL INTERIM CHAMP USA 2. EVANDER HOLYFIELD USA 2. VALERY VIKHOR (PABA) LAT 2. LOUIS DEL VALLE USA 3. WLADIMIR KLITSCHKO (WBAI-EBU) UKR 3. ALEXANDER GUROV (WBAI) UKR 3. FRANK LILES USA 4. MIKE TYSON USA 4. JAMES TONEY USA 4. DERRICK HARMON (USBA) USA 5. MICHAEL GRANT (NABF) USA 5. IMAMU MAYFIELD USA 5. ERIC HARDIN USA 6. DAVID TUA (USBA) N.Z 6. -

Low-Blows-Stephen-Glass.Pdf
http://www.lexisnexis.com.leo.lib.unomaha.edu/lnacui2api/deli... 89 of 127 DOCUMENTS The New Republic AUGUST 4, 1997 Low blows BYLINE: STEPHEN GLASS SECTION: Pg. 42 LENGTH: 1685 words HIGHLIGHT: Washington Diarist If you watched nothing but talk shows, you would think that the most common job in America is being an "expert." Every hour, a different expert hosts some form of guerrilla counseling on TV. It's because of all this competition that daytime- television experts now resemble academics in specialization. On the talk shows, there aren't just adultery experts, there are commentators for every form of illicit intercourse. This year alone I've seen two men and a woman who specialize in my-wife-slept-with-my-daughter's-boyfriend-who-is-a- high-school-quarterback cases. I've always assumed these pundits chose their fields for some autobiographical reason. So, a few days after Mike Tyson was disqualified for biting Evander Holyfield, I offered a half-dozen talk shows my services as a "biting expert." I'm someone who knows a lot, I said on their voice mail, about "chomping on flesh under extreme stress." Anxious for a cannibal, three panting producers called me back within two hours. I shared with them the story of how, in an unfortunate incident at summer camp when I was 11, the other cabin nerd tried to push my head into a toilet. With my forehead just inches from the water, I did the only thing I could think of: I lifted my head up and bit him on the cheek. -

The Epic 1975 Boxing Match Between Muhammad Ali and Smokin' Joe
D o c u men t : 1 00 8 CC MUHAMMAD ALI - RVUSJ The epic 1975 boxing match between Muhammad Ali and Smokin’ Joe Frazier – the Thriller in Manila – was -1- 0 famously brutal both inside and outside the ring, as a neW 911 documentary shows. Neither man truly recovered, and nor 0 did their friendship. At 64, Frazier shows no signs of forgetting 8- A – but can he ever forgive? 00 8 WORDS ADAM HIGGINBOTHAM PORTRAIT STEFAN RUIZ C - XX COLD AND DARK,THE BIG BUILDING ON of the world, like that of Ali – born Cassius Clay .pdf North Broad Street in Philadelphia is closed now, the in Kentucky – began in the segregated heartland battered blue canvas ring inside empty and unused of the Deep South. Born in 1944, Frazier grew ; for the first time in more than 40 years. On the up on 10 acres of unyielding farmland in rural Pa outside, the boxing glove motifs and the black letters South Carolina, the 11th of 12 children raised in ge that spell out the words ‘Joe Frazier’s Gym’ in cast a six-room house with a tin roof and no running : concrete are partly covered by a ‘For Sale’ banner. water.As a boy, he played dice and cards and taught 1 ‘It’s shut down,’ Frazier tells me,‘and I’m going himself to box, dreaming of being the next Joe ; T to sell it.The highest bidder’s got it.’The gym is Louis. In 1961, at 17, he moved to Philadelphia. r where Frazier trained before becoming World Frazier was taken in by an aunt, and talked im Heavyweight Champion in 1970; later, it would also his way into a job at Cross Brothers, a kosher s be his home: for 23 years he lived alone, upstairs, in slaughterhouse.There, he worked on the killing i z a three-storey loft apartment. -
Boxing Edition
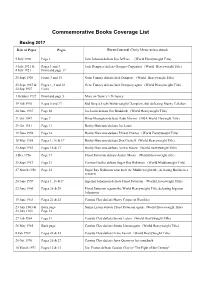
Commemorative Books Coverage List Boxing 2017 Date of Paper Pages Event Covered (Daily Mirror unless stated) 5 July 1910 Page 3 Jack Johnson defeats Jim Jeffries (World Heavyweight Title) 3 July 1921 & Pages 1 and 3 Jack Dempsey defeats Georges Carpentier (World Heavyweight Title) 4 July 1921 Front and page 17 25 Sept 1926 Front, 3 and 15 Gene Tunney defeats Jack Dempsey (World Heavyweight Title) 23 Sept 1927 & Pages 1, 3 and 18 Gene Tunney defeats Jack Dempsey again (World Heavyweight Title) 24 Sep 1927 Front 1 October 1927 Front and page 5 More on Tunney v Dempsey 19 Feb 1930 Pages 5 and 22 Kid Berg is Light Welterweight Champion after defeating Mushy Callahan 24 June 1937 Page 30 Joe Louis defeats Jim Braddock (World Heavyweight Title) 21 Oct 1947 Page 7 Rinty Monaghan defeats Dado Marino (NBA World Flyweight Title) 29 Oct 1951 Page 11 Rocky Marciano defeats Joe Louis 19 June 1954 Page 14 Rocky Marciano defeats Ezzard Charles (World Heavyweight Title) 18 May 1955 Pages 1, 16 & 17 Rocky Marciano defeats Don Cockell (World Heavyweight Title) 23 Sept 1955 Pages 16 & 17 Rocky Marciano defeats Archie Moore (World Heavyweight Title) 3 Dec 1956 Page 17 Floyd Patterson defeats Archie Moore (World Heavyweight title) 25 Sept 1957 Page 23 Carmen Basilio defeats Sugar Ray Robinson (World Middleweight Title) 27 March 1958 Page 23 Sugar Ray Robinson wins back the Middleweight title, defeating Basilio in a rematch 28 June 1959 Pages 1, 16 &17 Ingemar Johansson defeats Floyd Patterson (World Heavyweight Title) 22 June 1960 Pages 28 & 29 Floyd Patterson -

Welc Me Roxanne Soileau Assistant Mgr
101 Westwood Drive Lafayette, Louisiana 70506 (337) 233-4428 A P A R T M E N T S Bayou Shadows Staff November 2014 Martha Carver Community Mgr. Welc me Roxanne Soileau Assistant Mgr. Margeaux Graham Assistant Mgr. New Residents Bonnie Labbie Assistant Mgr. Kishment McClosky Assistant Mgr. Fred Begnaud Maint. Engineer We are so happy that you chose George Moreau Maint. Supervisor to stay with us at Bayou Shadows. Eddie Sanders Maint. Engineer Harold Morrison Maint. Tech. James Nolan Maintenance Tech. Rodrick Gary Maintenance Tech. Nicholas Parfait Maintenance Tech. Darnell Sonnier General Maint. James Meche General Maint. Nicholas Menard General Maint. Happy birthday to all of our Patricia Vallier Janitorial Staff residents celebrating a birthday Genevieve Leopaul Janitorial Staff this month!! Mary Collins Janitorial Staff OFFICE HOURS Monday–Friday 8:30 a.m.–5:30 p.m. Saturday 10 a.m.–4 p.m. After-hours Answering Service (337) 572-4131 Turkey Time Eat to Sleep www.bayou-shadows.com Dark turkey meat has more fat and Did you know that certain foods Did you know that you can: calories than white meat, but dark can help you sleep while others may • Pay rent online meat is rich in iron, zinc, and vitamins keep you up at night? If you want a • Submit service requests B6 and B12. peaceful rest, choose oatmeal, • Post items of interest almonds, herbal teas, cherries and All on our website. Sign up now. Memories Repurposed dark chocolate. Foods that can leave Please go to our website and rate us If you have T-shirts you no longer you restless include alcohol, caffeine, with our resident survey .. -

CONGRESSIONAL RECORD—HOUSE October 12, 2000
October 12, 2000 CONGRESSIONAL RECORD—HOUSE 22401 of the bill (H.R. 3244) to combat trafficking Lewis and Samoan heavyweight boxer Mr. Speaker, as we say in the Sa- of persons, especially into the sex trade, David Tua. moan language (the gentleman spoke slavery, and slavery-like conditions, in the Mr. Speaker, it is against Samoan in Samoan) David Tua, which means, United States and countries around the tradition to be boastful and arrogant, Mr. Speaker, may your body be as in- world through prevention, through prosecu- but as a totally neutral observer, and tion and enforcement against traffickers, visible as the air and may your eyes be and through protection and assistance to with all due respect, Lennox Lewis is as bright as the sun. May you be vic- victims of trafficking, shall make the fol- going to painfully wake up the next torious in battle. All our hopes and as- lowing correction: morning and count how many ribs he pirations are with you, David Tua. In section 2002(a)(2)(A)(ii), strike ‘‘June 7, has left, and then he will wonder if he 1999,’’ and insert ‘‘December 13, 1999,’’. was hit by either a dump truck or a D– f The Senate concurrent resolution 9 caterpillar tractor, after fighting EXCHANGE OF SPECIAL ORDER was concurred in. against David Tua. TIME You see, Mr. Speaker, this guy, David A motion to reconsider was laid on Mr. PAUL. Mr. Speaker, I ask unani- the table. Tua, he has the heart and soul of a pure Polynesian warrior. He has got a nasty mous consent to claim the special f left hook and a deadly right hand order time of the gentleman from Indi- ana (Mr. -

Boxing, Governance and Western Law
An Outlaw Practice: Boxing, Governance and Western Law Ian J*M. Warren A Thesis submitted in fulfilment of the requirements of the degree of Doctor of Philosophy School of Human Movement, Performance and Recreation Victoria University 2005 FTS THESIS 344.099 WAR 30001008090740 Warren, Ian J. M An outlaw practice : boxing, governance and western law Abstract This investigation examines the uses of Western law to regulate and at times outlaw the sport of boxing. Drawing on a primary sample of two hundred and one reported judicial decisions canvassing the breadth of recognised legal categories, and an allied range fight lore supporting, opposing or critically reviewing the sport's development since the beginning of the nineteenth century, discernible evolutionary trends in Western law, language and modern sport are identified. Emphasis is placed on prominent intersections between public and private legal rules, their enforcement, paternalism and various evolutionary developments in fight culture in recorded English, New Zealand, United States, Australian and Canadian sources. Fower, governance and regulation are explored alongside pertinent ethical, literary and medical debates spanning two hundred years of Western boxing history. & Acknowledgements and Declaration This has been a very solitary endeavour. Thanks are extended to: The School of HMFR and the PGRU @ VU for complete support throughout; Tanuny Gurvits for her sharing final submission angst: best of sporting luck; Feter Mewett, Bob Petersen, Dr Danielle Tyson & Dr Steve Tudor;