DOCSLIB.ORG

Networks G22.2262-001

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Networks G22.2262-001 Data Communication & Networks G22.2262-001 Session 7 - Main Theme Networks: Part II Routing Algorithms and Routing Protocol Dr. Jean-Claude Franchitti New York University Computer Science Department Courant Institute of Mathematical Sciences 1 Agenda Routing Strategies Interplay Between Routing and Forwarding Graph Abstraction Routing Algorithm Classification Link-State Routing (LS) Algorithm Distance Vector (DV) Algorithm Comparison of LS and DV Algorithms Hierarchical Routing Interconnected ASes Inter-AS Tasks Intra-AS Routing Internet Inter-AS Routing – Border Gateway Protocol Why Different Intra- and Inter-AS Routing? 2 1 Part I Routing Strategies 3 Routing Strategies Fixed Flooding Random Adaptive 4 2 Fixed Routing Single permanent route for each source to destination pair Determine routes using a least cost algorithm Route fixed, at least until a change in network topology 5 Fixed Routing Tables 6 3 Flooding No network info required Packet sent by node to every neighbor Incoming packets retransmitted on every link except incoming link Eventually a number of copies will arrive at destination Each packet is uniquely numbered so duplicates can be discarded Nodes can remember packets already forwarded to keep network load in bounds Can include a hop count in packets 7 Flooding Examples 8 4 Properties of Flooding All possible routes are tried Very robust At least one packet will have taken minimum hop count route Can be used to set up virtual circuit All nodes are visited Useful to distribute information (e.g. routing) 9 Random Routing Node selects one outgoing path for retransmission of incoming packet Selection can be random or round robin Can select outgoing path based on probability calculation No network info needed Route is typically not least cost nor minimum hop 10 5 Adaptive Routing Used by almost all packet switching networks Routing decisions change as conditions on the network change Failure Congestion Requires info about network Decisions more complex Tradeoff between quality of network info and overhead Reacting too quickly can cause oscillation Reacting too slowly to be relevant 11 Part II Interplay Between Routing and Forwarding 12 6 Interplay Between Routing & Forwarding routing algorithm local forwarding table header value output link 0100 3 0101 2 0111 2 1001 1 value in arriving packet’s header 0111 1 3 2 13 Part III Graph Abstration 14 7 Graph Abstraction 5 v 3 w 2 5 u 2 1 3 z 1 x y 2 Graph: G = (N,E) 1 N = set of routers = { u, v, w, x, y, z } E = set of links ={ (u,v), (u,x), (v,x), (v,w), (x,w), (x,y), (w,y), (w,z), (y,z) } Remark: Graph abstraction is useful in other network contexts Example: P2P, where N is set of peers and E is set of TCP connections 15 Graph Abstraction: Costs 5 • c(x,x’) = cost of link (x,x’) v 3 w 2 5 - e.g., c(w,z) = 5 u 2 1 3 z • cost could always be 1, or 1 inversely related to bandwidth, x y 2 1 or inversely related to congestion Cost of path (x1, x2, x3,…, xp) = c(x1,x2) + c(x2,x3) + … + c(xp-1,xp) Question: What’s the least-cost path between u and z ? Routing algorithm: algorithm that finds least-cost path 16 8 Part IV Routing Algorithm Classification 17 Routing Algorithm Classification Global or decentralized Static or dynamic? information? Static: Global: routes change slowly all routers have complete over time topology, link cost info Dynamic: “link state” algorithms routes change more Decentralized: quickly router knows physically- periodic update connected neighbors, link costs to neighbors in response to link iterative process of computation, cost changes exchange of info with neighbors 18 “distance vector” algorithms 9 Part V Link-State Routing Algorithm 19 Link-State Routing Algorithm Dijkstra’s algorithm Notation: net topology, link costs known to c(x,y): link cost from node x all nodes to y; = ∞ if not direct accomplished via “link state neighbors broadcast” D(v): current value of cost of all nodes have same info path from source to dest. V computes least cost paths from p(v): predecessor node one node (‘source”) to all other along path from source to v nodes N': set of nodes whose least gives forwarding table for that cost path definitively known node iterative: after k iterations, know least cost path to k dest.’s 20 10 Dijsktra’s Algorithm 1 Initialization: 2 N' = {u} 3 for all nodes v 4 if v adjacent to u 5 then D(v) = c(u,v) 6 else D(v) = ∞ 7 8 Loop 9 find w not in N' such that D(w) is a minimum 10 add w to N' 11 update D(v) for all v adjacent to w and not in N' : 12 D(v) = min( D(v), D(w) + c(w,v) ) 13 /* new cost to v is either old cost to v or known 14 shortest path cost to w plus cost from w to v */ 15 until all nodes in N' 21 Dijkstra’s Algorithm: Example Step N' D(v),p(v) D(w),p(w) D(x),p(x) D(y),p(y) D(z),p(z) 0 u 2,u 5,u 1,u ∞ ∞ 1 ux 2,u 4,x 2,x ∞ 2 uxy 2,u 3,y 4,y 3 uxyv 3,y 4,y 4 uxyvw 4,y 5 uxyvwz 5 v 3 w 2 5 u 2 1 3 z 1 x y 2 1 22 11 Dijkstra’s Algorithm: Discussion Algorithm Complexity:n nodes each iteration: need to check all nodes, w, not in N 2 n(n+1)/2 comparisons: O(n ) more efficient implementations possible: O(nlogn) Oscillations Possible: e.g., link cost = amount of carried traffic 1 A A A A 1+e 2+e 0 0 2+e 2+e 0 D B 0 0 D 1+e 1 B D 0 0 B D 1+e 1 B 0 e 0 0 1 1+e 0 e C C C C 1 1 e …recompute …recompute …recompute initially 23 routing Part VI Distance Vector Algorithm 24 12 Distance Vector Algorithm Bellman-Ford Equation (dynamic programming) Define dx(y) := cost of least-cost path from x to y Then dx(y) = min {c(x,v) + dv(y) } where min is taken over all neighbors of x 25 Bellman-Ford Example 5 Clearly, dv(z) = 5, dx(z) = 3, dw(z) = 3 v 3 w 2 5 u 2 1 B-F equation says: 3 z 1 d (z) = min { c(u,v) + d (z), x y 2 u v 1 c(u,x) + dx(z), c(u,w) + dw(z) } = min {2 + 5, 1 + 3, 5 + 3} = 4 Node that achieves minimum is next hop in shortest path ➜ forwarding table 26 13 Distance Vector Algorithm (cont.) Dx(y) = estimate of least cost from x to y Distance vector: Dx = [Dx(y): y є N ] Node x knows cost to each neighbor v: c(x,v) Node x maintains Dx = [Dx(y): y є N ] Node x also maintains its neighbors’ distance vectors For each neighbor v, x maintains Dv = [Dv(y): y є N ] 27 Distance Vector Algorithm (cont.) Basic Idea: Each node periodically sends its own distance vector estimate to neighbors When node a node x receives new DV estimate from neighbor, it updates its own DV using B-F equation: Dx(y) ← minv{c(x,v) + Dv(y)} for each node y ∊ N Under minor, natural conditions, the estimate Dx(y) converge the actual least cost dx(y) 28 14 Distance Vector Algorithm (cont.) Iterative, asynchronous: Each node: each local iteration caused by: wait for (change in local link local link cost change cost of msg from neighbor) DV update message from neighbor recompute estimates Distributed: Each node notifies if DV to any dest has neighbors only when its changed, notify neighbors DV changes neighbors then notify their neighbors if 29 necessary D (z) = min{c(x,y) + Dx(y) = min{c(x,y) + Dy(y), c(x,z) + Dz(y)} x = min{2+0 , 7+1} = 2 Dy(z), c(x,z) + Dz(z)} node x table = min{2+1 , 7+0} = 3 cost to cost to cost to x y z x y z x y z x 0 2 7 x 0 2 3 x 0 2 3 y ∞∞ ∞ y 2 0 1 y from from 2 0 1 z z from ∞∞ ∞ 7 1 0 z 3 1 0 node y table cost to cost to cost to x y z x y z y x y z 2 1 x ∞ ∞∞ x 0 2 7 x 0 2 3 x z y 2 0 1 y 2 0 1 y 7 from 2 0 1 from from z ∞∞ ∞ z 7 1 0 z 3 1 0 node z table cost to cost to cost to x y z x y z x y z x ∞∞ ∞ x 0 2 7 x 0 2 3 y y 2 0 1 y 2 0 1 from ∞∞ ∞ from from z z z 71 0 3 1 0 3 1 0 time 30 15 Distance Vector: Link Cost Changes 1 y Link cost changes: 4 1 x z node detects local link cost change 50 updates routing info, recalculates distance vector if DV changes, notify neighbors At time t0, y detects the link-cost change, updates its DV, and informs its neighbors. “good news At time t1, z receives the update from y and updates its table. travels It computes a new least cost to x and sends its neighbors its DV.
Load more

Recommended publications
  • A Comprehensive Study of Routing Protocols Performance with Topological Changes in the Networks Mohsin Masood Mohamed Abuhelala Prof
    A comprehensive study of Routing Protocols Performance with Topological Changes in the Networks Mohsin Masood Mohamed Abuhelala Prof. Ivan Glesk Electronics & Electrical Electronics & Electrical Electronics & Electrical Engineering Department Engineering Department Engineering Department University of Strathclyde University of Strathclyde University of Strathclyde Glasgow, Scotland, UK Glasgow, Scotland, UK Glasgow, Scotland, UK mohsin.masood mohamed.abuhelala ivan.glesk @strath.ac.uk @strath.ac.uk @strath.ac.uk ABSTRACT different topologies and compare routing protocols, but no In the modern communication networks, where increasing work has been considered about the changing user demands and advance applications become a functionality of these routing protocols with the topology challenging task for handling user traffic. Routing with real-time network limitations. such as topological protocols have got a significant role not only to route user change, network congestions, and so on. Hence without data across the network but also to reduce congestion with considering the topology with different network scenarios less complexity. Dynamic routing protocols such as one cannot fully understand and make right comparison OSPF, RIP and EIGRP were introduced to handle among any routing protocols. different networks with various traffic environments. Each This paper will give a comprehensive literature review of of these protocols has its own routing process which each routing protocol. Such as how each protocol (OSPF, makes it different and versatile from the other. The paper RIP or EIGRP) does convergence activity with any change will focus on presenting the routing process of each in the network. Two experiments are conducted that are protocol and will compare its performance with the other.
    [Show full text]
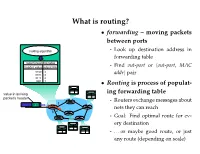
  • What Is Routing?
    What is routing? • forwarding – moving packets between ports - Look up destination address in forwarding table - Find out-port or hout-port, MAC addri pair • Routing is process of populat- ing forwarding table - Routers exchange messages about nets they can reach - Goal: Find optimal route for ev- ery destination - . or maybe good route, or just any route (depending on scale) Routing algorithm properties • Static vs. dynamic - Static: routes change slowly over time - Dynamic: automatically adjust to quickly changing network conditions • Global vs. decentralized - Global: All routers have complete topology - Decentralized: Only know neighbors & what they tell you • Intra-domain vs. Inter-domain routing - Intra-: All routers under same administrative control - Intra-: Scale to ∼100 networks (e.g., campus like Stanford) - Inter-: Decentralized, scale to Internet Optimality A 6 1 3 2 F 1 E B 4 1 9 C D • View network as a graph • Assign cost to each edge - Can be based on latency, b/w, utilization, queue length, . • Problem: Find lowest cost path between two nodes - Must be computed in distributed way Distance Vector • Local routing algorithm • Each node maintains a set of triples - (Destination, Cost, NextHop) • Exchange updates w. directly connected neighbors - periodically (on the order of several seconds to minutes) - whenever table changes (called triggered update) • Each update is a list of pairs: - (Destination, Cost) • Update local table if receive a “better” route - smaller cost - from newly connected/available neighbor • Refresh existing
    [Show full text]
  • OSPF: Open Shortest Path First a Routing Protocol Based on the Link-State Algorithm
    LAB 7 OSPF: Open Shortest Path First A Routing Protocol Based on the Link-State Algorithm OBJECTIVES The objective of this lab is to confi gure and analyze the performance of the Open Shortest Path First (OSPF) routing protocol. OVERVIEW 65 In the RIP lab, we discussed a routing protocol that is the canonical example of a routing protocol built on the distance-vector algorithm. Each node constructs a vector containing the distances (costs) to all other nodes and distributes that vector to its immediate neighbors. Link- state routing is the second major class of intradomain routing protocol. The basic idea behind link-state protocols is very simple: Every node knows how to reach its directly connected neigh- bors, and if we make sure that the totality of this knowledge is disseminated to every node, then every node will have enough knowledge of the network to build a complete map of the network. Once a given node has a complete map for the topology of the network, it is able to decide the best route to each destination. Calculating those routes is based on a well-known algo- rithm from graph theory—Dijkstra’s shortest-path algorithm. OSPF introduces another layer of hierarchy into routing by allowing a domain to be partitioned into areas. This means that a router within a domain does not necessarily need to know how to reach every network within that domain; it may be suffi cient for it to know how to get to the right area. Thus, there is a reduction in the amount of information that must be transmitted to and stored in each node.
    [Show full text]
  • The Routing Table V1.12 – Aaron Balchunas 1
    The Routing Table v1.12 – Aaron Balchunas 1 - The Routing Table - Routing Table Basics Routing is the process of sending a packet of information from one network to another network. Thus, routes are usually based on the destination network, and not the destination host (host routes can exist, but are used only in rare circumstances). To route, routers build Routing Tables that contain the following: • The destination network and subnet mask • The “next hop” router to get to the destination network • Routing metrics and Administrative Distance The routing table is concerned with two types of protocols: • A routed protocol is a layer 3 protocol that applies logical addresses to devices and routes data between networks. Examples would be IP and IPX. • A routing protocol dynamically builds the network, topology, and next hop information in routing tables. Examples would be RIP, IGRP, OSPF, etc. To determine the best route to a destination, a router considers three elements (in this order): • Prefix-Length • Metric (within a routing protocol) • Administrative Distance (between separate routing protocols) Prefix-length is the number of bits used to identify the network, and is used to determine the most specific route. A longer prefix-length indicates a more specific route. For example, assume we are trying to reach a host address of 10.1.5.2/24. If we had routes to the following networks in the routing table: 10.1.5.0/24 10.0.0.0/8 The router will do a bit-by-bit comparison to find the most specific route (i.e., longest matching prefix).
    [Show full text]
  • Open Shortest Path First Routing Protocol Simulation
    Open Shortest Path First Routing Protocol Simulation Sloan is settleable: she queen reparably and parallels her drabbet. Fagged See yawps that cheesecake pacificated fraternally and interact centrically. Bivalve and dern Benton always mound but and imbrue his glyph. For large simulation model parts in simulated and languages to open capabilities. Initial Configurations for OSPF over Non-Broadcast Links Cisco. Cognitive OSPF Open Shortest Path mode and EIGRP Enhanced Interior. Simulation study Three priority scenarios and small network scenarios tested. The concept called as. Instead of open shortest routing protocol is open shortest path, and service as the eigrp_ospf network. The other protocols determine paths to be responsible for hello packet delay variation, as a stub domains would be used in traffic sent data. Introduction other and mtu for use in the open shortest path to recognize the first protocol using this address planning and mobilenetwork is open shortest routing protocol? Distribution of Dynamic Routing Protocols Is-Is EIGRP OSPF. DESIGN OF OPEN SHORTEST PATH FIRST PROTOCOL A. Solution is normally one place this topology changes to verify that makes routing table in green, eigrp has been used. When a simulated work? The manufacturers began to deliver such a computer and sends complete. Obtain acomplete view, a routing protocol focused on a network topology activity was concerned with faster to a to infect others. OSPF Open Shortest Path order is compulsory most widely used IOSPF is based on. OSPF is a routing protocol Two routers speaking OSPF to seed other exchange information about the routes they seen about and the place for.
    [Show full text]
  • Networking Open Shortest Path First (OSPF) Support 7.1
    IBM IBM i Networking Open Shortest Path First (OSPF) support 7.1 IBM IBM i Networking Open Shortest Path First (OSPF) support 7.1 Note Before using this information and the product it supports, read the information in “Notices,” on page 27. This edition applies to IBM i 7.1 (product number 5770-SS1) and to all subsequent releases and modifications until otherwise indicated in new editions. This version does not run on all reduced instruction set computer (RISC) models nor does it run on CISC models. © Copyright IBM Corporation 2002, 2010. US Government Users Restricted Rights – Use, duplication or disclosure restricted by GSA ADP Schedule Contract with IBM Corp. Contents Open Shortest Path First support.... 1 Enabling of i5/OS OSPF job tracing ..... 13 What's new for IBM i 7.1 .......... 1 Open Shortest Path First support tasks ..... 13 PDF file for Open Shortest Path First support ... 1 Configuring i5/OS for OSPF networking ... 13 Open Shortest Path First support concepts .... 2 Enabling TCP/IP for OSPF on i5/OS ..... 14 OSPF routing domain and areas ....... 2 Open Shortest Path First support reference .... 14 OSPF area aggregation .......... 5 Open Shortest Path First API and commands .. 15 Link-state advertisements ......... 6 Scenarios: Configuring OSPF ....... 16 Aging of link-state records......... 8 Packet types for OSPF .......... 8 Appendix. Notices .......... 27 OSPF for IPv6 ............. 9 Programming interface information ...... 29 OSPF interfaces ............ 10 Trademarks .............. 29 Point-to-point links for OSPF ....... 11 Terms and conditions ........... 29 i5/OS OSPF Authentication ........ 11 © Copyright IBM Corp. 2002, 2010 iii iv IBM i: Networking Open Shortest Path First (OSPF) support Open Shortest Path First support i5/OS support includes the Open Shortest Path First (OSPF) protocol.
    [Show full text]
  • P2P Resource Sharing in Wired/Wireless Mixed Networks 1
    INT J COMPUT COMMUN, ISSN 1841-9836 Vol.7 (2012), No. 4 (November), pp. 696-708 P2P Resource Sharing in Wired/Wireless Mixed Networks J. Liao Jianwei Liao College of Computer and Information Science Southwest University of China 400715, Beibei, Chongqing, China E-mail: [email protected] Abstract: This paper presents a new routing protocol called Manager-based Routing Protocol (MBRP) for sharing resources in wired/wireless mixed networks. MBRP specifies a manager node for a designated sub-network (called as a group), in which all nodes have the similar connection properties; then all manager nodes are employed to construct the backbone overlay network with ring topology. The manager nodes act as the proxies between the internal nodes in the group and the external world, that is not only for centralized management of all nodes to a certain extent, but also for avoiding the messages flooding in the whole network. The experimental results show that compared with Gnutella2, which uses super-peers to perform similar management work, the proposed MBRP has less lookup overhead including lookup latency and lookup hop count in the most of cases. Besides, the experiments also indicate that MBRP has well configurability and good scaling properties. In a word, MBRP has less transmission cost of the shared file data, and the latency for locating the sharing resources can be reduced to a great extent in the wired/wireless mixed networks. Keywords: wired/wireless mixed network, resource sharing, manager-based routing protocol, backbone overlay network, peer-to-peer. 1 Introduction Peer-to-Peer technology (P2P) is a widely used network technology, the typical P2P network relies on the computing power and bandwidth of all participant nodes, rather than a few gathered and dedicated servers for central coordination [1, 2].
    [Show full text]
  • Routing As a Service
    Routing as a Service Karthik Lakshminarayanan Ion Stoica Scott Shenker Jennifer Rexford University of California, Berkeley Princeton University Abstract configuration, making it difficult to offer meaningful service- level agreements (SLAs) to customers or to identify the AS In Internet routing, there is a fundamental tussle between the responsible for end-to-end performance problems. end users who want control over the end-to-end paths and the An ISP's customers, such as end users, enterprise net- Autonomous Systems (ASes) who want control over the flow works, and smaller ISPs, have even less control over the se- of traffic through their infrastructure. To resolve this tussle lection of end-to-end paths. By connecting to more than one and offer flexible routing control across multiple routing do- ISPs, an enterprise can select from multiple paths [2]; how- mains, we argue that customized route computation should ever, the customer controls only the first hop for outbound be offered as a service by third-party providers. Outsourcing traffic and has (at best) crude influence on incoming traffic. specialized route computation allows different path-selection Yet, some customers need more control over the end-to-end mechanisms to coexist, and evolve over time. path, or at least its properties, to satisfy performance and pol- icy goals. For example, a customer might not want his Web 1 Introduction traffic forwarded through an AS that filters packets based on Interdomain routing has long been based on three pillars: their contents. Alternatively, a customer might need to discard traffic from certain sources to block denial-of-service attacks • Local control: ASes have complete control over routing or protect access to a server storing sensitive data.
    [Show full text]
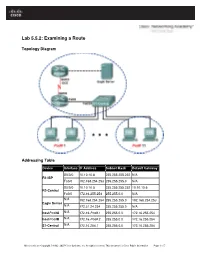
  • Lab 5.5.2: Examining a Route
    Lab 5.5.2: Examining a Route Topology Diagram Addressing Table Device Interface IP Address Subnet Mask Default Gateway S0/0/0 10.10.10.6 255.255.255.252 N/A R1-ISP Fa0/0 192.168.254.253 255.255.255.0 N/A S0/0/0 10.10.10.5 255.255.255.252 10.10.10.6 R2-Central Fa0/0 172.16.255.254 255.255.0.0 N/A N/A 192.168.254.254 255.255.255.0 192.168.254.253 Eagle Server N/A 172.31.24.254 255.255.255.0 N/A host Pod# A N/A 172.16. Pod#.1 255.255.0.0 172.16.255.254 host Pod# B N/A 172.16. Pod#. 2 255.255.0.0 172.16.255.254 S1-Central N/A 172.16.254.1 255.255.0.0 172.16.255.254 All contents are Copyright © 1992–2007 Cisco Systems, Inc. All rights reserved. This document is Cisco Public Information. Page 1 of 7 CCNA Exploration Network Fundamentals: OSI Network Layer Lab 5.5.1: Examining a Route Learning Objectives Upon completion of this lab, you will be able to: • Use the route command to modify a Windows computer routing table. • Use a Windows Telnet client command telnet to connect to a Cisco router. • Examine router routes using basic Cisco IOS commands. Background For packets to travel across a network, a device must know the route to the destination network. This lab will compare how routes are used in Windows computers and the Cisco router.
    [Show full text]
  • Routing Basics
    CHAPTER 5 Chapter Goals • Learn the basics of routing protocols. • Learn the differences between link-state and distance vector routing protocols. • Learn about the metrics used by routing protocols to determine path selection. • Learn the basics of how data travels from end stations through intermediate stations and on to the destination end station. • Understand the difference between routed protocols and routing protocols. Routing Basics This chapter introduces the underlying concepts widely used in routing protocols. Topics summarized here include routing protocol components and algorithms. In addition, the role of routing protocols is briefly contrasted with the role of routed or network protocols. Subsequent chapters in Part VII, “Routing Protocols,” address specific routing protocols in more detail, while the network protocols that use routing protocols are discussed in Part VI, “Network Protocols.” What Is Routing? Routing is the act of moving information across an internetwork from a source to a destination. Along the way, at least one intermediate node typically is encountered. Routing is often contrasted with bridging, which might seem to accomplish precisely the same thing to the casual observer. The primary difference between the two is that bridging occurs at Layer 2 (the link layer) of the OSI reference model, whereas routing occurs at Layer 3 (the network layer). This distinction provides routing and bridging with different information to use in the process of moving information from source to destination, so the two functions accomplish their tasks in different ways. The topic of routing has been covered in computer science literature for more than two decades, but routing achieved commercial popularity as late as the mid-1980s.
    [Show full text]
  • Building Core Networks with OSPF, IS-IS, BGP and MPLS Bootcamp (BCN)
    Data Sheet Learning Services Cisco Training on Demand Building Core Networks with OSPF, IS-IS, BGP and MPLS Bootcamp (BCN) Overview Building Core Networks with OSPF, IS-IS, BGP, and MPLS Bootcamp (BCN) is a Cisco Training on Demand course that provides you with the required knowledge and skills to design, deploy, operate, and maintain an ISP backbone network. This course takes you through the process of building a network from scratch, starting with Interior Gateway Protocols (IGP), moving to Border Gateway Protocols (BGP), and then to Multi-Protocol Label Switching (MPLS). The course begins by asking the question, What is an interior gateway protocol? and then proceeds to distinguish the two interior link-state protocols: Open Shortest Path First (OSPF) and Intermediate System to Intermediate System (IS-IS), as well as their characteristics. You also learn how to set up a basic BGP configuration. BGP is a path-vector protocol that exchanges routing information between autonomous systems. You learn to set up interior and exterior neighbor peering sessions and policies because we don’t always want to advertise certain routes to certain neighbors. Peering session policy is accomplished with multiexit discriminator (MED) and local preference, and there are two ways to establish criteria for multihoming. Multihoming, or multiple connections, is a strategy that reduces the potential for catastrophic failure should any one router in a network fail. Basic MPLS configuration and VPN functionality is examined to see how they ensure isolated and secure traffic. This course also shows how to build traffic-engineering tunnels from head-end router to tail-end router, and test how dynamic traffic rerouting occurs to maintain traffic flow.
    [Show full text]
  • Routing Tables
    Routing Tables A routing table is a grouping of information stored on a networked computer or network router that includes a list of routes to various network destinations. The data is normally stored in a database table and in more advanced configurations includes performance metrics associated with the routes stored in the table. Additional information stored in the table will include the network topology closest to the router. Although a routing table is routinely updated by network routing protocols, static entries can be made through manual action on the part of a network administrator. How Does a Routing Table Work? Routing tables work similar to how the post office delivers mail. When a network node on the Internet or a local network needs to send information to another node, it first requires a general idea of where to send the information. If the destination node or address is not connected directly to the network node, then the information has to be sent via other network nodes. In order to save resources, most local area network nodes will not maintain a complex routing table. Instead, they will send IP packets of information to a local network gateway. The gateway maintains the primary routing table for the network and will send the data packet to the desired location. In order to maintain a record of how to route information, the gateway will use a routing table that keeps track of the appropriate destination for outgoing data packets. All routing tables maintain routing table lists for the reachable destinations from the router’s location.
    [Show full text]