Solving: 2 Equations with 2 Unknowns

Solving: 2 Equations with 2 unknowns using a graphing calculator

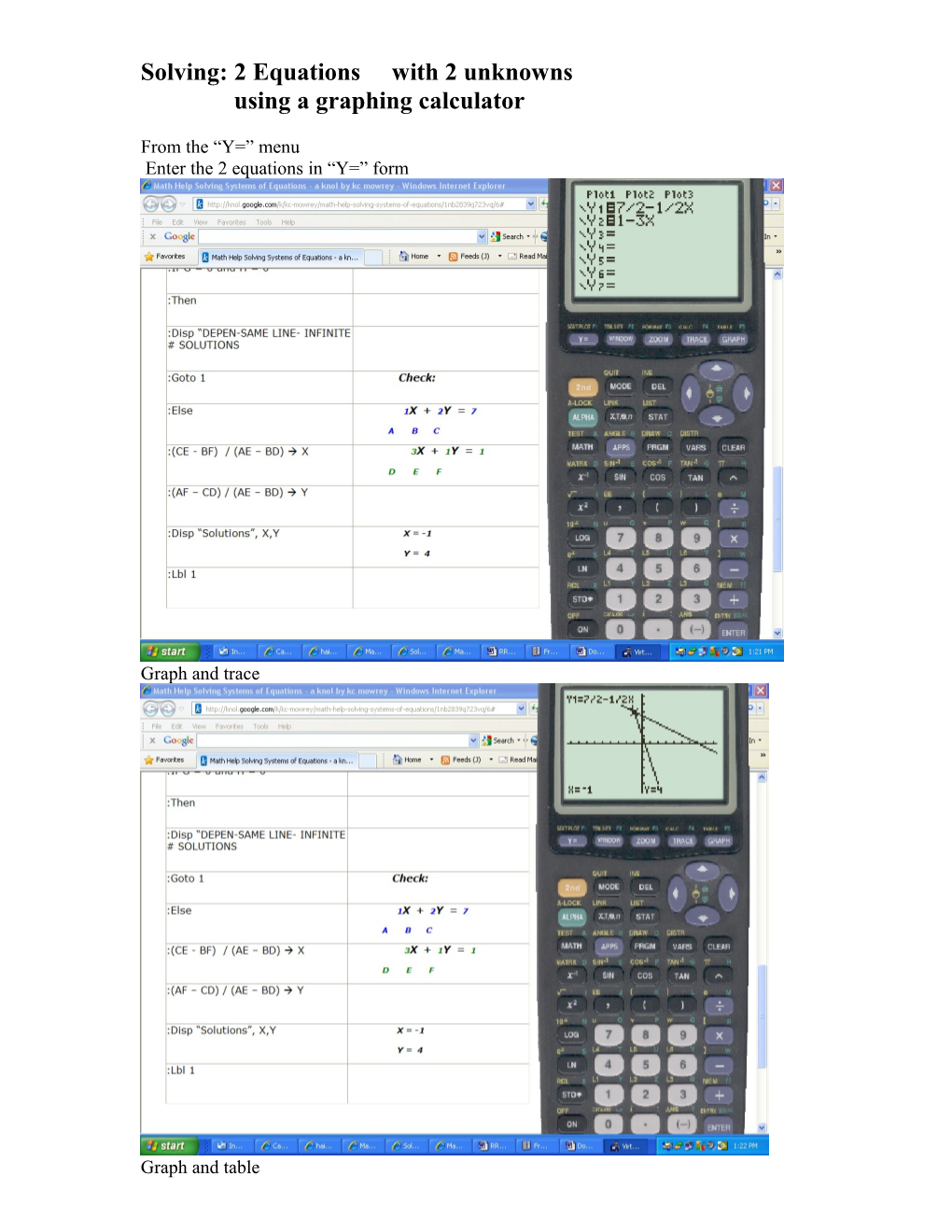
From the “Y=” menu Enter the 2 equations in “Y=” form

Graph and trace

Graph and table Graph and Calc (the Trace 2nd menu)

Use #5 Intersect Enter 1st curve—Enter 2nd curve—Enter Guess?—Enter Intersection- ->

You can also RREF from standard form RREF

Finding the solution to 2 equations with 2 unknowns using RREF = reduced row echelon form in the MATRIX menu of a TI 83 - TI 84+

given 2 equations

Slope - Intercept change to Standard Form Matrix form form y = 33x + 0 -33x + y = 0 -33 1 0 y = 24x + 18 -24x + y = 18 -24 1 18

Go to MATRIX Edit

Set matrix A into a 2 x 3 form Enter the matrix derived from the standard form equations -33 1 0 -24 1 18 Return to the home screen (second mode (quit) brings you to the home screen) return to the MATRIX menu and choose the “MATH” menu go up (or down) to B: rref(

Enter This puts rref( on the main screen return to the MATRIX menu select MATRIX A (it is the default) from the MATRIX menu just press Enter Enter This brings up: rref ([A] ‌ ‌‌|1 0 2 | | 0 1 66|

the solution is 1x + 0y = 2 0x + 1y = 66

or (x, y) (2, 66)

You can also program your calculator to solve using the program I wrote Also available on line at http://knol.google.com/k/kc-mowrey/math-help-solving-systems-of- equations/1nb2839q723vq/6# Solving Systems of Linear Equations

This program will solve a system of two linear equations written in the form: Ax + By = C Dx + Ey = F

Name = SLVSYSTM

:Prompt A,B,C {Prompt is in PRGM under I/O}

:Prompt D, E, F

:(AE – BDG { is the STO key}

:(CE - BF)H

:If G = 0 and H ≠ 0 {If is in PRGM under CTL} {= and ≠ are in TEST } :Then {Then is in PRGM under CTL}

:Disp “INCONST- PARALLEL-NO {Disp is in PRGM under I/O} SOLUTIONS”

:Goto 1 {Goto is in PRGM under CTL}

:Else {Else is in PRGM under CTL}

:If G = 0 and H = 0

:Disp “DEPEN-SAME LINE- INFINITE # SOLUTIONS

:Goto 1 Check:

:Else 1X + 2Y = 7 A B C :(CE - BF) / (AE – BD)  X 3X + 1Y = 1 D E F :(AF – CD) / (AE – BD)  Y

:Disp “Solutions”, X,Y X = -1 Y = 4 :Lbl 1