Multiple-Choice Questions s19

Essential Mathematical Methods 3 & 4 CASChapter 17 Continuous random variables and their probability distributions

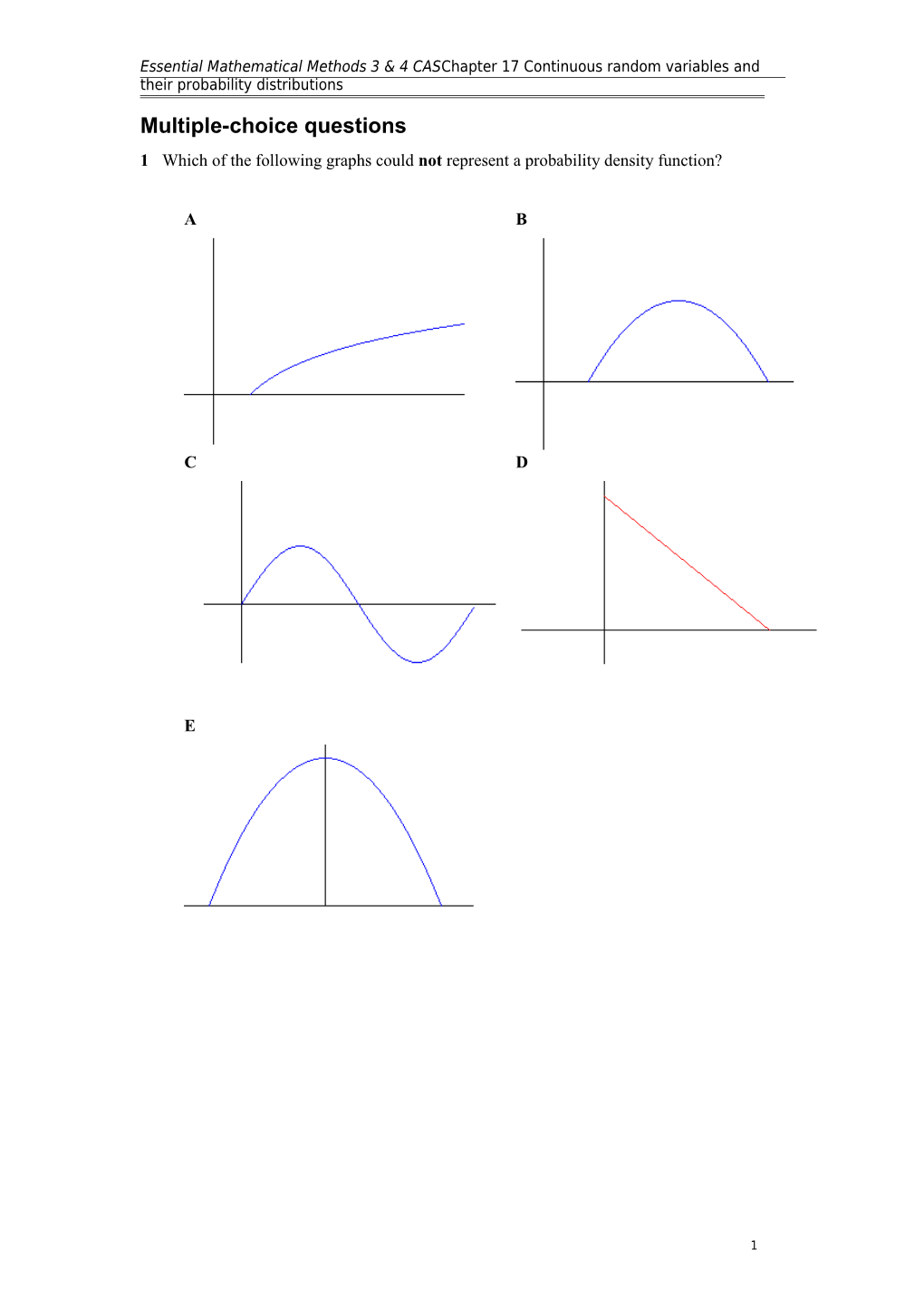
Multiple-choice questions 1 Which of the following graphs could not represent a probability density function?

1 Essential Mathematical Methods 3 & 4 CASChapter 17 Continuous random variables and their probability distributions

2 If the function f(x) = 4x represents a probability density function, then which of the following could be the domain of f?

2 A 0 < x < 2

B 0 < x < 2 C –0.5 < x < 0.5 D 0 < x < 0.25 E –1 < x < 1

3 If a random variable X has probability density function  1 ekx 0  x  f (x)   k  0 otherwise then k is equal to: A (1 – e–1)–1 B –e–1 C 1 + e–1 D 1 – e–1 E –1

4 If a random variable X has probability density function  3  x 2  4x  5 0  x  5 f (x)  50  0 x  0 or x  5 then the mode of X is: A 0 B 1 C 2.5 D 3.125 E 5

5 If a random variable X has probability density function

 3  x 2  4x  5 0  x  5 f (x)  50  0 x  0 or x  5 then the mean of X is: A 0 B 1 C 2.5 D 3.125 E 5

6 The continuous random variable X has probability density function f given by

where a is a constant. The value of a is: A 0 1 B 3 1 C 9 D 1 E –1

7 If a random variable X has a probability density function

 3  x 2  4 0  x  1 f (x)  13  0 x  0 or x  1 then the variance of X is closest to: A 0.290 B 0.084 C 0.354 D 0.519 E 0.290

8 If a random variable X has a probability density function 5e5x x  0 f (x)    0 otherwise then the median of X is closest to A 0.5 B 0.2

C loge 2

D loge 0.4 log 2 E e 5

9 If a random variable X has a probability density function 3  (x3  5x2  6x) 0  x  2 f (x)  8  0 otherwise then the mode of X is closest to: A 0 B C 1 D 0.785 E 2.549

10 Which of the following graphs represents Pr(1  x  2), where the random variable X has a probability distribution function:

loge x 1 x  e f (x)    0 otherwise A B

11 The continuous random variable X has probability density function f given by:

E(X2) is equal to: 4 A 3 64 B 3 C 24 D 4 E 0.25

12 If random variable X has a mean X = 5 and a standard deviation X = 4, and Y = 2  X then:

A Y = 5 and  Y = 4

B Y = –3 and  Y = –2

C Y = –3 and  Y = 4

D Y = –3 and  Y = 2

E Y = 3 and  Y = 2

13 If the time between customer arrivals at a bank is a random variable X with mean of 75 seconds and a variance of 9 minutes then 95% of the times between arrivals are between: A 66 seconds and 84 seconds B 57 seconds and 93 seconds C 69 seconds and 81 seconds D 72 seconds and 78 seconds E 48 seconds and 102 seconds

14 The time (in minutes) between arrivals of trains at a station is a random variable X which has probability density function:

The probability that Laura will have to wait less than 7 minutes for a train, given that she waits at least 5 minutes is closest to: A 0.339 B 0.493 C 0.688 D 0.948 E 0.016

15 A teacher has determined that the top 20% of students will be given an ‘A’ on the mathematics examination. If the distribution of scores on the examination is a random variable X with probability density function

then the minimum score required to be awarded an ‘A’ is closest to: A 60 B 70 C 80 D 90 E 95

Short-answer questions (technology-free) 1 The probability density function of X is given by: kx 1  x  2 f(x) =   0 x  1 or x  2 a Find k. b Find Pr(1 < X < 1.5).

2 Check whether or not the following are probability density functions over the given range:

1  x 2  4 0  x  1 a f(x) = 2  0 x  0 or x  1

1  2  x  4 b f(x) = 2 0 x  2 or x  4

3 The probability density function of the age of babies, X years, brought into a clinic is given by: 3  x(2  x) 0  x  2 f(x) = 4  0 otherwise If 60 babies are brought in on a particular day, how many are expected to be less than 8 months old?

4 The probability density function of X is given by:   sin(2x) 0  x  f(x) =  2  0 otherwise Find the mean, median and mode of X.

5 A random variable X has a probability density function given by:

 x  1  x  3 f(x) = 4 0 otherwise a Find E(X) and Var(X). b Find the median value of X. c Find the mode of X.

6 A random variable with a uniform distribution has a probability density function given by:  1  a  x  b f(x) = b  a  0 otherwise a Find E(X). b Find Var(X).

7 The probability density function for the surface area in cm2 of a virus placed on a culture plate after 8 hours is approximately: ex  0  x  3 f(x) = 19  0 otherwise Use this to find the probability that a culture plate has a surface area more than 2 cm2.

8 The time taken to complete a crossword puzzle is found to be a continuous random variable with mean 35 minutes and standard deviation 10 minutes. Find an (approximate) interval for the time it takes for 95% of people to complete the puzzle.

Extended-response questions The time it takes to complete a task (in hours) is a random variable X with probability density function

where c is a constant. 1 Find the value of c.

2 Sketch the graph of this distribution.

3 Write down the most likely time taken to complete the task.

4 Find the probability that the time taken to complete the task will be: a more than 0.8 hours b between 0.4 and 0.8 hours

Answers to Chapter 16 Test A

Answers to multiple-choice questions

1 C 2 A 3 D 4 E 5 D 6 C 7 B 8 E 9 D 10 A 11 C 12 C 13 C 14 B 15 B

Answers to short-answer questions (technology-free)

1 a 2/3 b 5/12 2 a no b yes 5 3 15 9 π π π 4 , , 4 4 4 13 11 5 a , 6 36

b 5 c 3 b  a 6 a 2

(b  a) 2 b 12

7 0.6682 to four decimal places 8 15 minutes to 55 minutes

Answers to extended-response questions

25 1 36 2

(0.6, 2.5)

3 0.6 hours 1 4 a 8 157 b 216