CAPITAL INVESTMENT
Capital Investment (Capital Budgeting) involves the allocation of large amounts of resources in long-term investments.
Examples: => Replacement of Equipment => Expansion of Existing Product Lines => Development of New Product Lines => Intangibles: => Research & Development => Patents => Advertising campaigns
Success: Texas Instruments - semiconductor in 1950s and 1960s; microchip in 1970s
Microsoft - Bought Quick and Dirty Operating System for $50,000
Failure: Ford Edsel (Loss of $250 million in 1957-59, or approximately $2 billion today)
Once the Investment is made, it is almost impossible to back out. Unlike a surplus of inventory which can be quickly corrected, an unutilized refinery just sits vacant.
The firm's existence is a series of capital investment decisions that are necessary for the company to grow, remain competitive, etc.
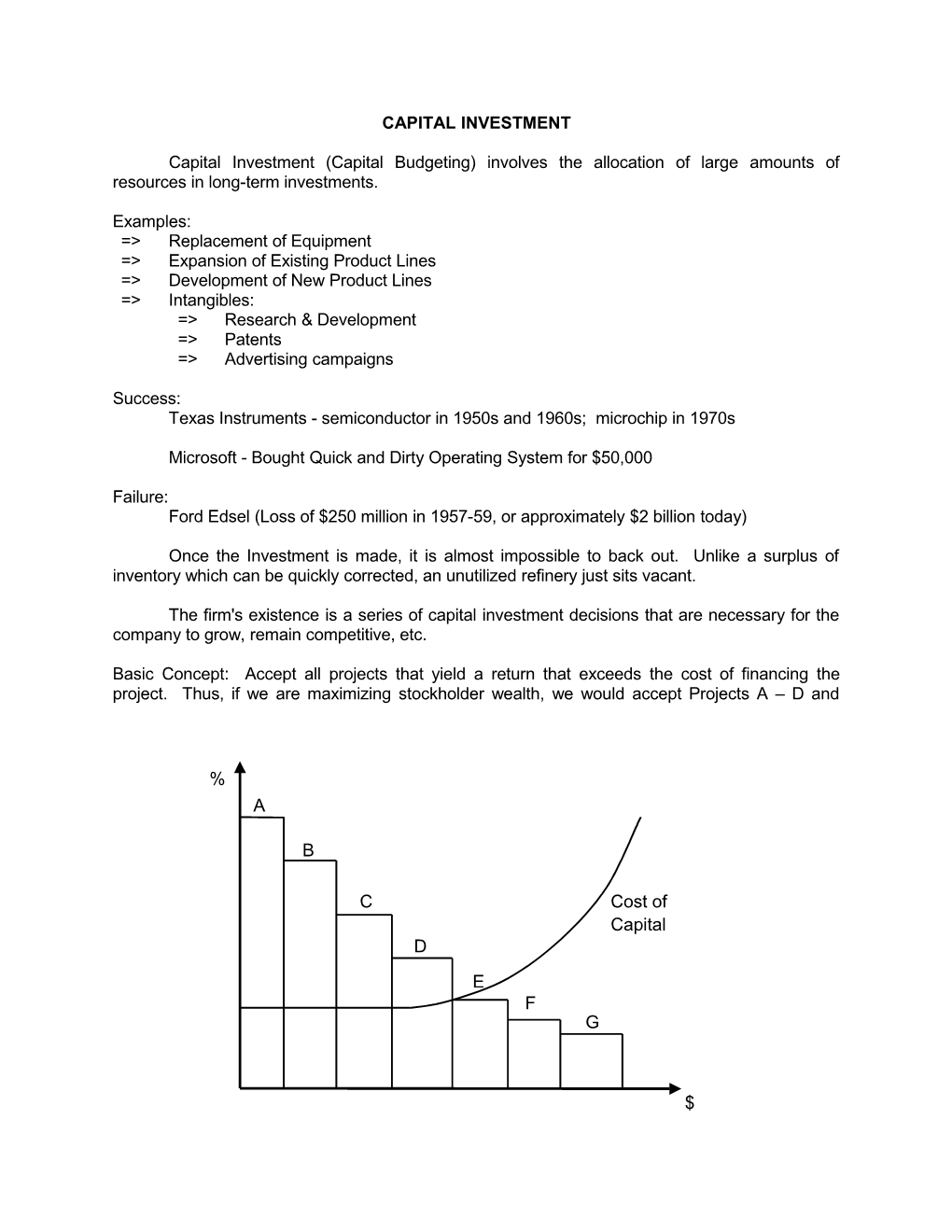
Basic Concept: Accept all projects that yield a return that exceeds the cost of financing the project. Thus, if we are maximizing stockholder wealth, we would accept Projects A – D and
% A
B
C Cost of Capital D E F G
$ reject the remainder:
Numerous investment alternatives exist. We need a means of ranking the projects from best to worst in order to select those that are most valuable to the firm; i.e., a means of evaluating and ranking proposals.
The primary concern in the investment decision regards cash flows:
=> Incremental Revenues => Incremental Costs => Taxes => Depreciation considerations => Investment in Working Capital => Cost Savings
Any cash inflow or outflow.
EVALUATION TECHNIQUES
A) Payback Period Proj. A Proj. B ------Year 0 (3,000) (3,000) Year 1 1,000 2,000 Year 2 2,000 1,000 Year 3 3,000 4,000
Payback = 2 years Payback = 2 years
Both projects have a payback of two years, so the payback method indicates that the two projects are equally desirable.
Problems:
1) Ignores the Time Value of Money
2) Ignores cash flows beyond the payback period
Project B returns $1,000 a year earlier than Project A and also returns an additional $1,000 in the last year.
Present Value (or Discounted) Payback, which utilizes the present value of each year's cash flow, overcomes the first problem, but not the second.
B) Present Value (Discounted) Payback Proj. A Proj. B ------Cash Flow PV of CF Cash Flow PV of CF Year 0 (3,000) (3,000) (3,000) (3,000) Year 1 1,100 1,000 2,200 2,000 Year 2 2,420 2,000 1,210 1,000 Year 3 3,000 2,254 4,000 3,005
PV Payback = 2 years PV Payback = 2 years
C) Net Present Value (NPV)
We need a methodology that takes into account all of the cash flows as well as the time value of money. Net Present Value is one such technique: NPV = PV of Cash Inflows - PV of Cash Outflows
Required Rate of Return = 10%
0 1 2 3
(4,000) 1,000 2,000 3,000
PV at 10% for 1 year 909 PV at 10% for 2 years 1,653 PV at 10% for 3 years 2,254
NPV @ 10% = 816
To calculate the NPV on an HP 10B financial calculator,
Clear All Enter 4000 and change the sign (+/-) and press CFj Enter 1000 and press CFj again Enter 2000 and press CFj Enter 3000 and press CFj Enter 10 and press I/YR Press the shift key and press NPV
NPV represents the increase in the value of the firm that occurs by accepting the project. In other words, it represents the amount by which the value of the project exceeds its cost. Proof: Year 0 Investment 4,000 Cash Flow - Year 1 1,000 Return of Investment (600) Less: Interest (400) (10%*$4,000) ------Year 1 Investment 3,400 Return of Investment 600 Return of Investment (1,660) ------Cash Flow - Year 2 2,000 Year 2 Investment 1,740 Less: Interest (340) (10%*$3,400) Return of Investment (2,826) ------Return of Investment 1,660 Surplus Return (1,086) PVIF10%,3 0.7513 Cash Flow - Year 3 3,000 ------Less: Interest (174) (10%*$1,740) Present Value 816 ------Return of Investment 2,826
The problem with NPV is that there is no consideration of cost, or what is referred to as size disparity. Proj. A Proj. B ------Present Value of Inflows 1,050 125 Cost (1,000) (100) ------Net Present Value 50 25
If these are mutually exclusive projects (i.e., choose one or the other, but not both), the NPV criterion says to choose Project A. While Project A increases the value of the firm by twice the amount of Project B, it costs ten times as much. The NPV does not indicate how efficiently money has been invested.
Capital Rationing - the allocation of a scarce resource, in this case money.
D) Profitability Index (PI) (or Benefit-Cost Ratio) - a measure of efficiency of investment
PV of Inflows Profitability Index PV of Outflows
PIA = 1.05 PIB = 1.25
The interpretation of PI is that of the amount of money in today's dollar terms that you get per dollar of investment. This indicates how efficiently you have invested money.
E) Internal Rate of Return (IRR) Another measure of the efficiency of investment is the Internal Rate of Return. When someone asks what rate of return an investment is earning, they mean the Internal Rate of Return. The IRR can be defined as
PV of Inflows @ IRR = PV of Outflows @ IRR or NPV @ IRR = 0
This is the actual rate of interest that is being earned on the investment. While the present value and annuity tables can be used in certain cases, the more general situation of uneven cash flows requires that the IRR be found by trial and error.
From the previous example, it is clear that more than 10% is being earned, since the NPV is $816.
Calculating the IRR on the HP 10B is almost identical to calculating the NPV:
Clear All Enter 4000 and change the sign (+/-) and press CFj Enter 1000 and press CFj again Enter 2000 and press CFj Enter 3000 and press CFj Press the shift key and press IRR/YR
The Internal Rate of Return is 19.44%
Year 0 Investment 4,000 Cash Flow -- Year 1 1,000 Return of Investment (222) Less: Interest (778) (19.44% * $4,000) Year 1 Investment 3,778 Return of Investment 222 Return of Investment (1,266) Year 2 Investment 2,512 Cash Flow -- Year 2 2,000 Return of Investment 2,512 Less: Interest (734) (19.44% * $3,778) Surplus Return 0 Return of Investment 1,266
Cash Flow -- Year 3 3,000 Less: Interest (488) (19.44% * $2,512) Return of Investment 2,512
Hence, it is the rate of interest earned on the funds that remain invested within the project. This is the economic interpretation of the mathematical solution.
Year 0 Year 1 Year 2 Year 3 NPV @ 10% PI @ 10% IRR Project A (15,000) 10,000 10,000 0 2,355 1.16 21.5% Project B (48,000) 30,000 30,000 0 4,066 1.08 16.3%
Which project is better? The major difference is the costs of the projects.
Year 0 Year 1 Year 2 Year 3 NPV @ 10% PI @ 10% IRR Project C (10,000) 8,000 5,600 0 1,901 1.19 24.9% Project D (10,000) 0 0 17,000 2,772 1.28 19.3%
Which project is better? The major difference is the timing of the cash flows.
Note that all three measures agree as to whether a project is acceptable or not. The conflict is in the ranking of the investment proposals.
Note also that the Profitability Index, a measure of efficiency of investment, does not always agree with IRR in terms of which is the most efficient use of funds.
THE REINVESTMENT ASSUMPTION
Consider the following two projects, their NPVs, PIs, and IRRs.
Project X Year 0 Year 1 Year 2 Year 3 Cash Flows (886) 100 100 1,100
NPV @ 10% = 114 PI @ 10% = 1.13 IRR = 15.0%
Project Y Year 0 Year 1 Year 2 Year 3 Cash Flows (886) 900 150 55
NPV @ 10% = 97 PI @ 10% = 1.11 IRR = 20.0%
Most academicians claim that the conflict is a consequence of the reinvestment assumption. Net Present Value and Profitability Index assume reinvestment at the discount rate. Internal Rate of Return can be thought of as a special case of NPV (when it equals zero). Hence, it assumes reinvestment at the IRR.
Realistically, investments are made to maximize future wealth. Present value (discounted cash flow techniques) are used since we know the value of a dollar today. The reinvestment assumption is invoked in order to make the future value (terminal value) rankings consistent with the present value rankings. To see this, let's reinvest the cash flows of Projects X and Y at the discount rate of 10%.
Project X Year 0 Year 1 Year 2 Year 3 Cash Flows (886) 100 100 1,100 1.21 121 1.10 110 Terminal Value = 1,331
Project Y Year 0 Year 1 Year 2 Year 3 Cash Flows (886) 900 150 55 1.21 1,089 1.10 165 Terminal Value = 1,309
Since the costs are the same, the terminal values are both relative to the same size of investment. The $1,331 terminal value of Project X represents a 14.53% rate of return on an investment of $886 over three years while the $1,309 terminal value of Project Y is a 13.89% return on the initial investment. The difference in the terminal values of $22 has a present value of $17 which is the same as the difference in NPVs of the two projects (114 - 97 = 17). Thus, the terminal value rankings are consistent with the NPV and PI rankings that indicate Project X is superior to Project Y. Similarly, if the cash flows of each project are reinvested at their respective IRRs, the following is obtained:
Project X Year 0 Year 1 Year 2 Year 3 Cash Flows (886) 100 100 1,100 1.3223 132 1.15 115 Terminal Value = 1,347
Project Y Year 0 Year 1 Year 2 Year 3 Cash Flows (886) 900 150 55 1.4400 1,296 1.2000 180 Terminal Value = 1,531
Since the costs are identical, it is clear that Project Y is better since it maximizes future wealth, and agrees with the rankings of the IRRs. Moreover, the terminal value of $1,347 of Project X represents a 15% return on the cost of the project, while the $1,531 terminal value of Project Y is a 20% return on the investment in Project Y.
NON-NORMAL (NON-CONVENTIONAL) PROJECTS
Multiple Internal Rates of Return
Another criticism of the IRR method is that non-normal (or non-conventional) projects can have multiple IRRs. Consider the following project:
Year 0 Year 1 Year 2 Year 3 Year 4 Cash Flows (3,000) 2,000 4,500 3,500 (7,200)
Two IRRs exist: IRR1 = 3.2% and IRR2 = 47.16%. Which one is correct? Technically, both of them provide a solution to the discount rate that yields a Net Present Value = 0. The text refers to the question of "A borrowing rate or an investment rate?" in explaining why both are correct. Let's look at the 3.2% solution:
0 1 2 3 4
(3,000) 2,000 4,500 3,500 (7,200)
(3,000) * (1.032) = (3,096) + 2,000 (1,096) * (1.032) = (1,131) + 4,500 3,369 * (1.032) = 3,477 + 3,500 6,977 * (1.032) = 7,200 +( 7,200) Terminal Value = -0-
In this case, if you only require a 3.2% rate of return, your 3.2% rate of return and your principal are returned early in Year 2, and you only need to earn a return of 3.2% on the investment of surplus funds in order to have enough to payoff the cost of $7,200 at the end of the 4th year. The same is true with the IRR of 47.16%:
0 1 2 3 4
(3,000) 2,000 4,500 3,500 (7,200)
(3,000) * (1.4716) = (4,415) + 2,000 (2,415) * (1.4716) = (3,554) + 4,500 946 * (1.4716) = 1,393 + 3,500 4,893 * (1.4716) = 7,200 +( 7,200) Terminal Value = -0-
Because of the higher rate of return (47.16%), it takes longer to receive your rate of return and principal back (not until almost the end of the 2nd year since more of the cash flow is rate of return rather than return of principal) and you must now earn a 47.16% rate of return on the surplus funds to cover the cost of $7,200 at the end of the project life. (Check out the NPV of this project at 3.2% and 47.16% to verify that you'll get an NPV of zero.)
In short, the economic interpretation (that it is the return on invested funds) is lost because it also requires that the surplus funds earn the same rate of interest in order to cover the cash outflow in the last year. In fact, there is an IRR for each time that the cash flows change sign (in this case only two).
Many believe this is the primary reason to prefer NPV over IRR as an evaluation tool. Unfortunately, the concept of a rate of return (such as IRR) is preferred by almost all practitioners, particularly since it can be compared to the cost of funds or other investment opportunities.
Another shortfall to NPV is if the risk of the project (or future cash outflow) is higher than the risk of the average investment for the company. Consider the above example where the outflow is associated with a great deal of uncertainty about the cost (such as decommissioning a nuclear power plant). The greater uncertainty implies a higher discount rate be used in calculating the present value. Yet a higher discount rate makes the present value of the cost lower, and hence the project more attractive rather than less. One solution to this is to discount future cash outflows at a separate discount rate from the cash inflows. In fact, the more risky the future cash outflow, the lower the discount rate that should be employed. This has its own problems: as shown previously, if NPV assumes cash flows are reinvested at the discount rate, then an above-average risk project assumes that the (positive) cash flows will continue to be reinvested in above-average risk projects (i.e., earn a high rate of return) while the above-average risk costs (being discounted at a lower discount rate as mentioned) have a below-average cost of capital. Confusing, isn't it?
RELEVANT CASH FLOWS
Incremental Cash Flows
The relevant cash flows for investment analysis is the change in the cash flows that would occur by accepting a proposal, or what is referred to by the term incremental cash flows.
An opportunity cost is a cash flow given up as a consequence of a decision, and is generally defined as the next-best-alternative. Since an opportunity cost is a change in cash flow, it is relevant to the investment decision.
A sunk cost refers to past expenditures. Sunk costs are not relevant since they occurred in the past and the decision of whether or not to undertake a project does not change the past.
A general (simplified) format for analyzing a capital expenditure that considers all incremental cash flows is on the following page. Note that the relevant cash flows include those found on the income statement as well as those that are not on the income statement (such as working capital). Also, some cash flows are only reflected on the income statement in part (such as the gain or loss on the sale of an asset). CASH FLOW ANALYSIS PURCHASE/REPLACEMENT DECISION
Today Intervening Years Last Year
A.
H.
In a Purchase Decision, the relevant occurrences are A, D, E, F, H, I, J, and M In a Replacement Decision, the relevant occurrences are A through M 1If the asset is sold for less than the book value, the company incurs a loss which is tax-deductible. This loss reduces taxable income and thereby creates a tax savings equal to the difference between the market value of the asset and its book value multiplied by the tax rate: Loss * t If the asset is sold for more than the book value, the company must report the difference as a profit to be taxed as ordinary income to the extent that the profit is less than the accumulated depreciation for the asset: Gain * t In the event that the asset is sold for more than the original purchase price, the gain above the original purchase price is subject to the capital gains tax rate while the accumulated depreciation is taxed as ordinary income.
< > indicates that the cash flow is an outflow. t = applicable tax rate The Replacement Decision
The classic capital investment decision is that of whether or not to replace a large piece of equipment.
Example
Kinky's Copying Service is considering expanding operations to include new holographic color copying services. The new service is expected to result in additional sales of $600,000 in the first year, increasing by 12% per year as word of the color copies spreads. Labor and material costs are predicted to rise by $480,000 in the first year, increasing at a 6% annual rate due primarily to inflation. To accommodate the service, a new color copier will have to be purchased at a cost of $280,000. The new machine will be depreciated using the MACRS rates for 5-year assets (20%, 32%, 19.2%, 11.52%, 11.52%, 5.76%), even though you expect that after three years of 24-hour per day operation, it will have a resale value of only $50,000 and will have to be replaced. Since the holographic color copier can also make regular color copies, one of the small existing color copy machines can be sold to a local university for $45,000 rather than keeping it for the remaining three years of its useful life and scrapping it for $8,000. The existing color copy machine was purchased for $90,000 two years ago and is also being depreciated using the same MACRS rates for 5-year assets. The expanded service would use existing floor space in an adjacent room which would result in an allocation of depreciation totaling $5,000 per year. Also, $6,000 in administrative expenses would be allocated to the project each year; however, only $2,000 of the amount represents an actual increase in expenses not otherwise incurred by the firm (also increasing by 6% per year). The existing floor space of the adjacent room could be leased annually for $4,500 on a fixed three-year lease if the project is not accepted. An investment in working capital of $85,000 will initially be required, with additional increments of 8% per year due to both inflation and increasing sales, all of which will be recovered in the third year. Kinky's is in the 40% tax bracket. Calculate the net cash flows for each year of the project's life.
Solution
Year 1 Year 2 Year 3 Incremental Revenues Increased sales 600,000 x 1.12 = 672,000 x 1.12 = 752,640 Lost lease payments (4,500) (4,500) (4,500) Total Incremental Revenues 595,500 667,500 748,140
Incremental Costs Labor & materials 480,000 x 1.06 = 508,800 x 1.06 = 539,328 Administrative expense 2,000 x 1.06 = 2,120 x 1.06 = 2,247 Total Incremental Costs 482,000 510,920 541,575 Year 1 Year 2 Year 3 Incremental Depreciation New Machine 280,000 280,000 280,000 MACRS rate 20.00% 32.00% 19.20% New Depreciation 56,000 89,600 53,760
Old Machine 90,000 90,000 90,000 MACRS rate 19.20% 11.52% 11.52% Old Depreciation 17,280 10,368 10,368
Incremental Depreciation 38,720 79,232 43,392
Sale of Equipment Old machine - Yr. 0 Market Value 45,000 Book Value 43,200 (90,000*48%) Gain (loss) 1,800 Tax rate 40% Tax due (refund) 720
Old machine - Yr. 3 Market Value 8,000 Book Value 5,184 (90,000*5.76%) Gain (loss) 2,816 Tax rate 40% Tax due (refund) 1,126
New machine - Yr. 3 Market Value 50,000 Book Value 80,640 (280,000*28.8%) Gain (loss) (30,640) Tax rate 40% Tax due (refund) (12,256)
Working Capital Year Required Change 0 85,000 85,000 1 91,800 6,800 2 99,144 7,344 3 107,076 7,932 Putting it all together
Year 0 Year 1 Year 2 Year 3 Operating Cash Flows Revenues 595,500 667,500 748,140 Less: Costs (482,000) (510,920) (541,575) Less: Depreciation (38,720) (79,232) (43,392) Change in Taxable Income 74,780 77,348 163,173 Less: Taxes (40%) (29,912) (30,939) (65,269) Change in Net Income 44,868 46,409 97,904 Add-back depreciation 38,720 79,232 43,392 Change in Operating Cash Flow 83,588 125,641 141,296
Working Capital Requirements Additional Working Capital ( 85,000) ( 6,800) ( 7,344) ( 7,932) Working Capital Recovery 107,076
New Machine Purchase (280,000) Sale - Yr. 3 50,000 Tax Savings on Sale 12,256
Old Machine Sale - Yr. 0 45,000 Tax on Sale ( 720)
Lost Sale - Yr. 3 (8,000) Taxes Saved on Lost Sale 1,126 Total Incremental Cash Flows (320,720) 76,788 118,297 295,822