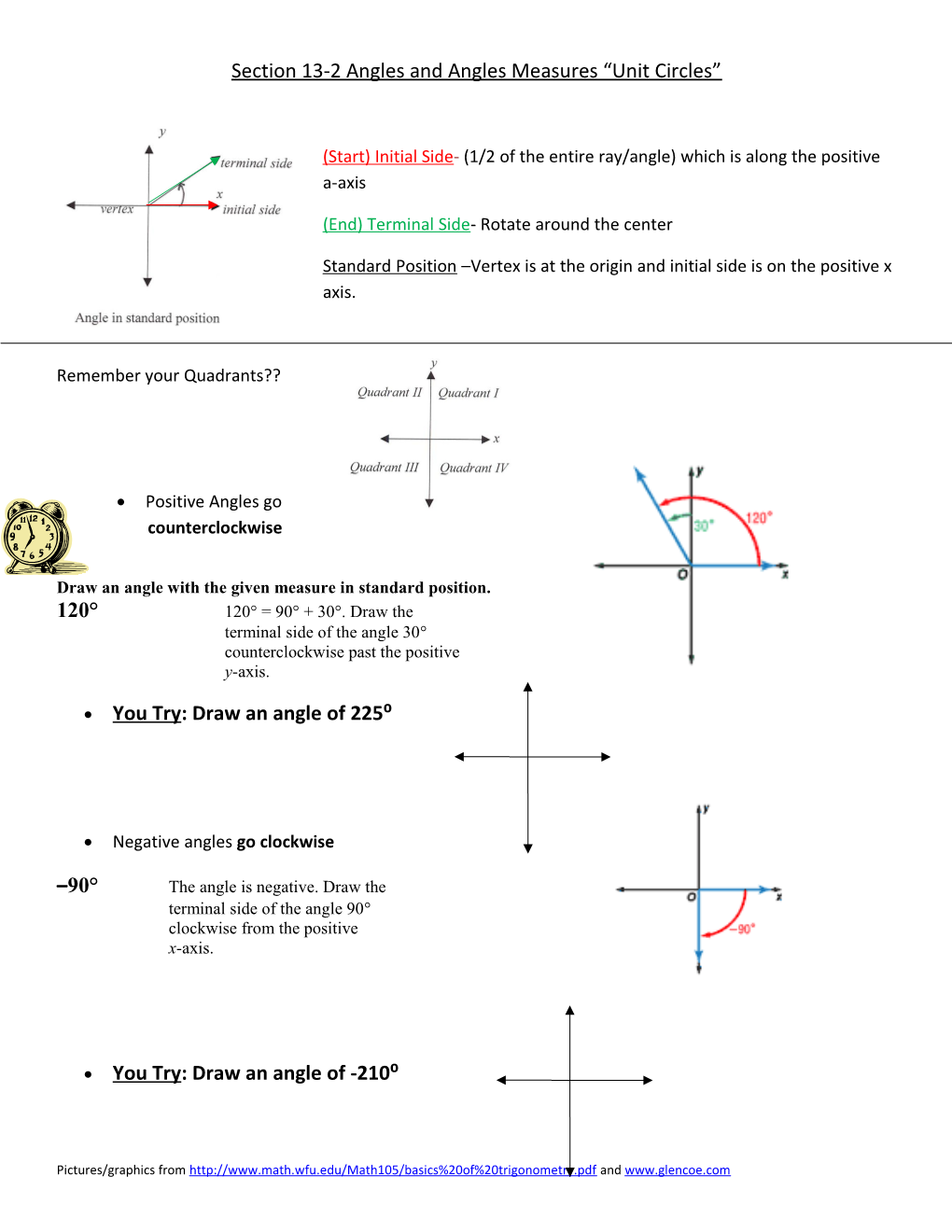
Section 13-2 Angles and Angles Measures Unit Circles

Section 13-2 Angles and Angles Measures “Unit Circles”

(Start) Initial Side- (1/2 of the entire ray/angle) which is along the positive a-axis

(End) Terminal Side- Rotate around the center

Standard Position –Vertex is at the origin and initial side is on the positive x axis.

Remember your Quadrants??

 Positive Angles go counterclockwise

Draw an angle with the given measure in standard position. 120° 120° = 90° + 30°. Draw the terminal side of the angle 30° counterclockwise past the positive y-axis.

 You Try: Draw an angle of 225⁰

 Negative angles go clockwise

–90° The angle is negative. Draw the terminal side of the angle 90° clockwise from the positive x-axis.

 You Try: Draw an angle of -210⁰

Pictures/graphics from http://www.math.wfu.edu/Math105/basics%20of%20trigonometry.pdf and www.glencoe.com  Multiple angles go round and round (remember 360⁰ is one turn)

765° 765° = 360° + 360° + 45°. Draw the terminal side of the angle 45° counterclockwise past the positive x-axis.

 You Try: Draw an angle of 495⁰

Converting to radians to degrees and vice versa

Degrees to radians-

260⁰ take degree and multiply by

So 260* = reduce to

Radians to degrees:

Radians to degrees—take the version and multiply by

So * = =

TRY THIS: Measure an Angle in Degrees and Radians ASTRONOMY- The Moon rotates on its axis about once every 27 Earth days. Find both the degree and radian measures of the angle through which it passes in 9 days. (Assume the rotation is counterclockwise.)

Coterminal angles

Coterminal angles -are angles that have the same end result of the graphs terminal position.

What does Means it works CO mean? together

Pictures/graphics from http://www.math.wfu.edu/Math105/basics%20of%20trigonometry.pdf and www.glencoe.com To find a coterminal angle add 360⁰ or subtract 360⁰ or any multiples of 360⁰

360⁰ Is the magic number!

Examples:

 Find 3 coterminals of 240⁰

240 + 360 = 600⁰

240-360 = -120⁰

240+360+360 = 960⁰

The “RAD” Magic number!

Examples:

 Give 2 other coterminals **Just carry the over to the answer.

 Radians-“New Measurement” Measurement of an angle, Θ, in the standard position. Where the arc length is 1 unit on the unit circle.

The unit circle

Pictures/graphics from http://www.math.wfu.edu/Math105/basics%20of%20trigonometry.pdf and www.glencoe.com You need to memorize this for a quiz grade!

Pictures/graphics from http://www.math.wfu.edu/Math105/basics%20of%20trigonometry.pdf and www.glencoe.com