Power Flow Examples 1.0 Introduction
We will solve the same problem in three different ways: - Full Newton - Fast decoupled - DC This problem and the solution by full Newton and the solution by decoupled power flow were adapted the problem in [1].
2.0 The Problem
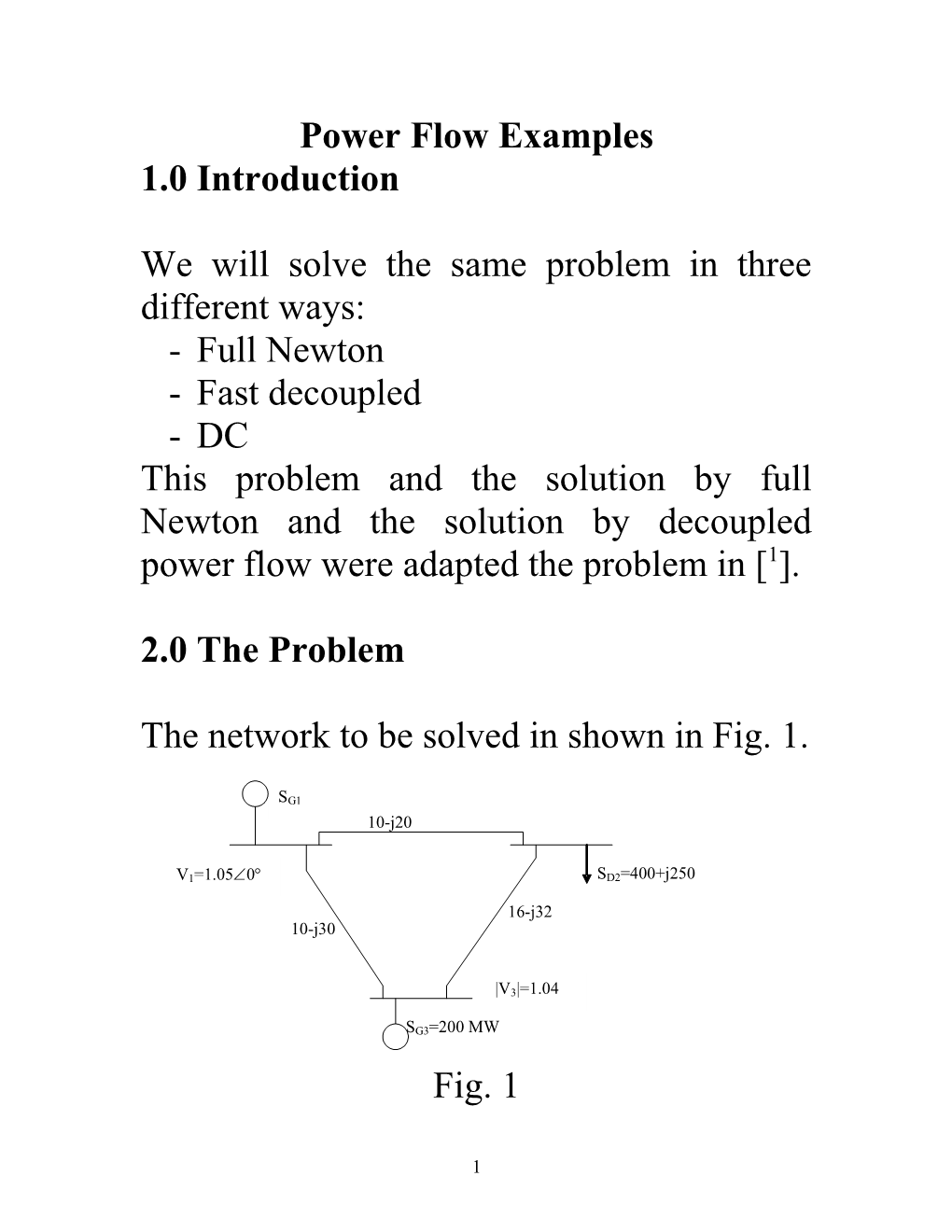
The network to be solved in shown in Fig. 1.
SG1 10-j20
V1=1.050 SD2=400+j250
16-j32 10-j30
|V3|=1.04
SG3=200 MW Fig. 1
1 In the network, charging capacitance has been neglected. All admittances are represented in pu on a 100 MVA base.
The Y-bus is given below: 20 j50 10 20 10 j30 Y 10 j20 26 j52 16 j32 10 j30 16 j32 26 j62 We will ignore reactive limits. Stopping criterion is |ΔPk|, |ΔQk|<ε=0.001.
3.0 Solution by Full Newton
Bus 1 is the swing bus, bus 2 is a PV bus, and bus 3 is a PQ bus. Therefore, the equations we need are:
P2 P2 (x) P2
P3 P3 (x) P3
Q2 Q2 (x) Q2
Using a 100 MVA base, P2=-4.0, P3=2.0, and Q2=-2.5. Then
2 P2 P2 (x) 4
P3 P3 (x) 2
Q3 Q3 (x) - 2.5 where: n Pi Vi Vk Gik cos(i k ) Bik sin(i k ) k 1 n Qi Vi Vk Gik sin(i k ) Bik cos(i k ) k 1 We use a “flat start” for the first iteration:
2 0 0 3 V2 1.0 And then the mismatch vector is:
P P2 1.14 4.0 2.8600 P 0.5616 2.0 1.4384 3 Q Q2 2.28 2.5 0.2200 We then get the Jacobian elements using
11 Pp (x) J pq V p Vq G pq sin( p q ) B pq cos( p q ) q
11 Pp (x) 2 J pp Q p (x) B pp V p p
3 21 Q p (x) J pq V p Vq G pq cos( p q ) B pq sin( p q ) q
21 Q p (x) 2 J pp Pp (x) G pp Vp p
12 Pp (x) J pq Vp G pq cos( p q ) B pq sin( p q ) Vq
12 Pp (x) Pp (x) J pp G pp V p V p V p
22 Q p (x) J pq Vp G pq sin( p q ) B pq cos( p q ) Vq
22 Q p (x) Q p (x) J pp Bpp Vp Vp Vp Again, using the “flat start” solution:
2 0 0 3 V2 1.0 We evaluate the above expressions to get the the Jaobian matrix, resulting in: 54.28 33.28 24.86 Note the off-diagonal submatrices are not all zero in this case, in contrast to the example J 33.28 66.04 16.64 given in “PowerFlowAlgorithm.doc,” (pg. 10) because here G≠0. 27.14 16.64 49.72 Our update equation is then
4 P ( j) ( j ) J x Q
54.28 33.28 24.86 2 2.8600 33.28 66.04 16.64 1.4384 3 27.14 16.64 49.72 V2 0.2200 Solution to this yields:
2 0.045263 0.007718 3 V2 0.026548 The updated solution is then 0 0.045263 0.045263 (1) (0) (0) x x x 0 0.007718 0.007718 1 0.026548 0.97345 For the second iteration, we get
51.724675 31.765618 21.302567 2 0.099218 32.981642 65.656383 15.379086 0.021715 3 27.14 16.64 48.103589 V2 0.050914 Solution to this yields:
2 0.001795 0.000985 3 V2 0.001767 The updated solution is then
5 0.045263 0.001795 0.04706 (2) (1) (1) x x x 0.007718 0.000985 0.00870 0.97345 0.001767 0.971684 For the third iteration, we get
51.596701 31.693866 21.147447 2 0.000216 32.933865 65.597585 15.379086 0.000038 3 27.14 17.396932 47.954870 V2 0.000143 We note that the mismatch vector satisfies the stopping criterion, but we will go ahead and complete this iteration to obtain:
2 0.000038 0.0000024 3 V2 0.0000044 The updated solution is then 0.04706 0.000038 0.04706 (3) (2) (2) x x x 0.00870 0.0000024 0.008705 0.971684 0.0000044 0.971680 So solution is obtained in 3 iterations.
4.0 Solution by FDC-nonalternating Recalling that the Y-bus is 20 j50 10 j20 10 j30 Y 10 j20 26 j52 16 j32 10 j30 16 j32 26 j62
6 To obtain the B-matrix, we use the imaginary parts of the Y-bus elements only, to get: 50 20 30 B 20 52 32 30 32 62 To obtain the matrix we will use to obtain updates on the angles, we remove the first row and column. Let’s call this B’: 52 32 B 32 62 Since bus 3 is a PV bus, we will not have a reactive power equation for it, and so to obtain the B-matrix on the update equation we need to remove the corresponding column and row. This will be the second row and column of the B’ matrix. We can call the resulting matrix B’’. It is B 52 Recalling from the above example that for the “flat start”
7 2 0 0 3 V2 1.0 The mismatch vector is: P 1.14 4.0 2.8600 0.5616 2.0 1.4384 Q 2.28 2.5 0.2200 Then the first iteration of the FDC (non- alternating) is: ( j ) P2 V 2 2.86 P3 ( j ) 52 32 2 B 1.0 V3 1.4384 32 62 3 ⋮ 1.04 Pn Vn
8 ( j ) Q2 V 2 Q3 ( j ) 0.22 B V V 52V2 3 1.0 ⋮ Qn Vn
Solution to these equations yields:
2 0.060483 3 0.008989
V2 0.0042308 The updated solution is then 0 0.060483 0.060483 (1) (0) (0) x x x 0 0.008989 0.008989 1 0.0042308 0.995769 The mismatch vector for the new solution is computed to be
9 P 0.175895 0.070951 Q 1.579042 And the solution is repeated. The algorithm requires 13 iterations before the stopping criterion on the mismatch vector is satisfied, and the solution obtained is the same as the solution obtained by the full Newton.
5.0 Solution by FDC-alternating This algorithm is the same as that presented in Section 4.0 except we will update the bus 3 reactive power mismatch vector with the angle solution obtained from the B’ matrix before we use the B’’ matrix to obtain the voltage update. This should result is less iterations.
6.0 Solution by DC Power Flow
10 The B’ matrix is used here, with the real power injection according to B P 52 32 B 32 62 4 P 2
52 32 2 4 32 623 2
2 - 0.0282 - 0.0145 4 - 0.0836 3 - 0.0145 - 0.0236 2 - 0.0109 Need to review the comparison here. Compare to full Newton solution: 0.04706 (3) x 0.008705 0.971680 To compare the two answers in terms of flows, one can use the approximate DC flow equation, given by:
Pkj Bkj (k j ) where the Bkj elements are given by
11 50 20 30 B 20 52 32 30 32 62 From the DC approximate solution:
P12 B12 (1 2 ) 20(0 .0836) 1.672
P13 B13 (1 3 ) 30(0 .0109) 0.327
P23 B23 (2 3 ) 32(.0836 .0109) 2.3264 From the Full Newton solution, but using the approximate DC flow equations:
P12 B12 (1 2 ) 20(0 .04706) 0.9412
P13 B13 (1 3 ) 30(0 .008705) 0.2415
P23 B23 (2 3 ) 32(.04706 .008705) 1.22736 0.04706 (3) x 0.008705 0.971680
12 1[] H. Saadat, “Power System Analysis,” 1999, McGraw-Hill.