Taylor Polynomials, Power Series

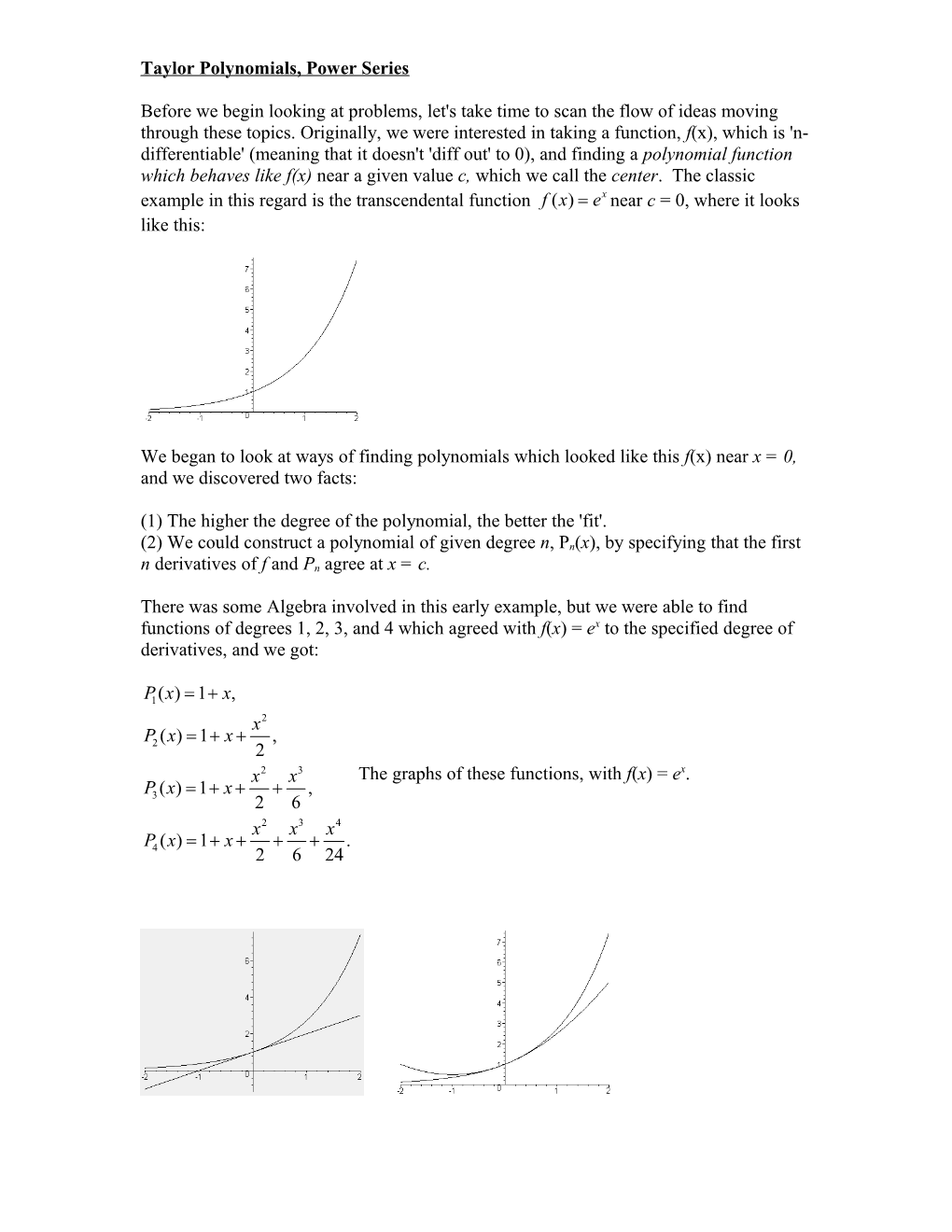
Before we begin looking at problems, let's take time to scan the flow of ideas moving through these topics. Originally, we were interested in taking a function, f(x), which is 'n- differentiable' (meaning that it doesn't 'diff out' to 0), and finding a polynomial function which behaves like f(x) near a given value c, which we call the center. The classic example in this regard is the transcendental function f( x ) = ex near c = 0, where it looks like this:

We began to look at ways of finding polynomials which looked like this f(x) near x = 0, and we discovered two facts:

(1) The higher the degree of the polynomial, the better the 'fit'. (2) We could construct a polynomial of given degree n, Pn(x), by specifying that the first n derivatives of f and Pn agree at x = c.

There was some Algebra involved in this early example, but we were able to find functions of degrees 1, 2, 3, and 4 which agreed with f(x) = ex to the specified degree of derivatives, and we got:

P1( x )= 1 + x , x2 P( x )= 1 + x + , 2 2 x2 x 3 The graphs of these functions, with f(x) = ex. P( x )= 1 + x + + , 3 2 6 x2 x 3 x 4 P( x )= 1 + x + + + . 4 2 6 24

You'll notice that the polynomial 'hugs the curve' closer as the degrees (and thus the degrees of agreement of the derivatives) increase.

Now, back to the 'Algebra' I mentioned earlier used to find these polynomials. It was noticed by a guy named Taylor that bringing the successive derivatives of a function f(x) and the associated polynomial Pn(x) into agreement generated a pattern in the coefficients of Pn. This gave rise to the Taylor Polynomial: (x- c )2 ( x - c )n P( x )= f( c) + fⅱ ( c )( x - c ) + f ( c ) + ... + f(n ) ( c ) n 2!n ! In cases where c = 0, we call this the McLaurin Polynomial.

From there, we took what seemed to be a strange turn, and began to look at the Power Series and it's Interval of Convergence (IOC). A power series is one of the form

n an ( x- c ) , where c is called the center of the series. We spent a great deal of time n=1 using the Ratio Test to determine where various power series converged. It always converged at the value c, but it could also converge for all values of distance R or less away from c, where R is the Radius Of Convergence (ROC).

c-R c c+R The range of values between c - R and c + R is known as the IOC, and the IOC may contain the endpoints as well, but they have to be individually tested. If it turns out that R = , then the IOC is the whole Real Line R .

Now we began to unite the previous topics, Power Series and Approximative Polynomials, by trying to find power series that would represent given functions of x, especially 'n-differentiable' ones. In other words given some f(x), and some specified center c, find a power series so that

n f( x )= an ( x - c ) , and determine for which values of x this statement was valid, n=1 namely it's IOC. We went about this in two ways. First, we tried the ol' Geometric Power Series Trick (8.9), most suitable for simple rational functions, using the fact that we know the sum of a convergent geometric series: a 1 1 = a( r )n , for example we saw = (x )n is a power series for , centered 1- r n=0 1- x n=0 1- x at x = 0, but the tricks got trickier as we moved the center around. Then, we returned to Taylor's conception of the problem - we could make the fit better and better by making higher-order derivatives agree. Why not extend this approach infinitely?. Thus we have the Taylor Series, (x- c )n f(n ) ( c ) , for n-differentiable functions like cos x, sin x, ex, and ln(x). Extending n=1 n! the first example we looked at, the Taylor series for f(x) = ex is xn xn f(x) = , and it's IOC is the entire Real Line, which means that ex and are n=1 n! n=1 n! functionally identical everywhere. So if we rounded out the group of pictures we looked xn at earlier by graphing ex and , the graphs would be as one: n=1 n!

Yeah, man, yeah. Anyway, the generalities have come to an end, and it's time to tend to the details:

Problems: (1) Find the Taylor Polynomial of degree 5 for f(x) = ln(x) w/ c = 1. (2) Find the McLaurin Polynomial of degree 5 for f(x) = cos(x). (3) Find the McLaurin Polynomial of degree 4 for f(x) = ex. (4) Determine the interval of convergence for the power series:  (1)n1(x 1)n (a)  n n1 2

 (x  2) n (b)  2 n1 n

 x n (c)  n0 n! (5) Find the derivative f '(x) and integral ∫ f(x) dx of f(x): (1) n1 (x  4)n1 (a) f (x)   n 1

 (1) n1 (x  3) n (b) f(x) =  n n1 n5 (6) Represent the rational function as a Geometric power series with the specified center c:

1 (a) ,c  4 2  x 3 (b) ,c  2 2x 1

1  1 (7) Given that  (x) n is a geometric power series for ,c  0, find a 1 x n0 1 x geometric power series for ln(1 + x) (tip: what is the relationship between the functions - think, like calculus - derivatives and integrals and stuff.)

 n x 3 (8) (a) Given that the Taylor series for ex =  , find a Taylor series for f(x) = ex n0 n! x2n+ 1 (b) Given that the Taylor Series for sin(x) = (- 1)n+1 , find a Taylor series for n=1 (2n + 1)! f(x) = sin(4x).

(- 1)n+1 (x - 1) n (c) Given that the Taylor Series for ln(x) = , find a Taylor series for n=1 n ln(x2).

Solutions: (1) Find the Taylor Polynomial of degree 5 for f(x) = ln(x) w/ c = 1. We need the first five derivatives, w/ 1 plugged into them. f( x )= ln x , f (1) = 0, 1 fⅱ( x )= = x-1 , f (1) = 1, x fⅱ( x )= - x-2 , f ⅱ (1) = - 1, fⅱⅱ( x )= 2 x-3 , f ⅱ (1) = 2, f(4)( x )= - 6 x- 4 , f (4) ( x ) = - 6, f(5)( x )= 24 x- 5 , f (5) ( x ) = 24. 1(x- 1)2 2( x - 1) 3 6( x - 1) 4 24( x - 1) 5 P( x )= 0 + 1( x - 1) - + - + 5 2! 3! 4! 5! (x- 1) ( x - 1)3 ( x - 1) 4 ( x - 1) 5 =(x - 1) - + - + . 2 3 4 5

(2) Find the McLaurin Polynomial of degree 5 for f(x) = cos(x). McLaurin means c = 0, and we're going to need five derivatives. f( x )= cos x , f (0) = cos(0) = 1 fⅱ( x )= - sin x , f (0) = 0, fⅱ( x )= - cos x , f ⅱ (0) = - 1, fⅱⅱ( x )= sin x , f ⅱ (0) = 0, f(4)( x )= cos x , f (4) (0) = 1, f(5)( x )= - sin x , f (5) (0) = - 1. 1x2 0 x 3 1 x 4 0 x 5 P( x )= 1 + 0 x - + + - note that the odd-degreed terms get knocked out. 5 2! 3! 4! 5! x21 x 4 (x )= 1 - + . 2! 4! (3) Find the McLaurin Polynomial of degree 4 for f(x) = ex. McLaurin means c = 0, and we need 4 derivatives. f( x )= ex , f (0) = 1, fⅱ( x )= ex , f (0) = 1, fⅱ( x )= ex , f ⅱ (0) = 1, fⅱⅱ( x )= ex , f ⅱ (0) = 1, f(4)( x )= ex , f (4) (0) = 1. x2 x 3 x 4 P( x )= 1 + x + + + . 4 2! 3! 4! (4)(a) Before we start, note that the center of the series is the number being subtracted from x, i.e. c = 1.

 (1)n1(x 1)n  n - ok, we want to use the logic of the ratio test, take the limit (note that I n1 2 ignore the (-1)n+1, since everything is absolute value) and get something of the form |x - 1| < R, using the fact that the ratio test yields convergence when the limit below is less than 1: u (x- 1)n+1 2 n ( x - 1) n ( x - 1) 2 n limn = lim * = lim * n n n+1 n n  n n un+1 2 ( x- 1) 2 2 ( x - 1) (x- 1) ( x - 1) =lim = < 1 when (get |x - 1| < R: * by 2) n 2 2 (x - 1) < 2. (The ROC is R = 2). Since we have c = 1, R = 2, the IOC (not including endpoints is the interval from 1-2 = -1 to 1 + 2 = 3.

-1 1 3 Now we test the endpoints by plugging them in and checking convergence: ゥ (- 1)n+1 (x - 1) n ( - 1) n + 1 ( - 2) n x = -1: 邋 n= n , note n=12 n = 1 2 (- 2)n = (2* - 1) n = 2 n ( - 1) n ,and ( - 1) n ( - 1) n+1 = - 1, so the above (after cancellation) (- 1)n+1 (2) n ( - 1) n becomes: n = = -1, which diverges, since it adds up to negative n=1 2 n=1 infinity. n+1 n (- 1) (2) n+1 x = 3: Plug in 3, and we have: n = =( - 1) , which diverges, since it n=1 2 n=1 bounces back and forth between 1 and 0 (as a sum, remember). So the IOC is (-1,3), which contains neither endpoint.

(b) Again, take the limit of ratios (note that the center is c = 2). (x- 2)n+1 n 2 n 2 *( x - 2) n ( x - 2) n 2 lim *= lim = lim *(x - 2) . n(n+ 1)2 ( x - 2)n n  ( n + 1) 2 ( x - 2) n n  ( n + 1) 2

= |x - 2| < 1 when it converges, so here the ROC is 1. ( 1: Quotient of lead coeff's.) the IOC would run from 2 - 1 = 1 to 2 + 1 = 3, so we need to check the endpoints: ゥ (x - 2)n ( - 1) n 1 x = 1: =,lim = 0, converges by AST. 邋 2 2n 2 n=1n n = 1 n n ゥ (x - 2)n (1) n 1 x = 3: 邋 2= 2 = 2 , convergent p-series. n=1n n = 1 n n = 1 n The IOC includes both endoints: [1,3].

 x n (c)  . Note that we have a McLaurin series: c = 0. Take the ratio limit: n0 n! xn+1 n! x n * x n ! x lim *= lim * = lim = 0 < 1 always, so the ROC is R = . n(n+ 1)! xn n  ( n + 1)* n ! x n n 0 n

top fixed, bottom to , limit is 0. This means that the IOC is the entire real line R .

(5)Remember, the action is on x, and we're just using the power rules for derivatives and integrals (in essence): d n n-1 邋an( x- c ) = na n ( x - c ) . dx n+1 n an ( x- c ) 邋an ( x- c ) dx = . n +1 (1) n1 (x  4)n1 (a) f (x)  ,  n 1 (- 1)n+1 (n + 1)( x - 4) n + 1 - 1 f( x )=邋 = ( - 1)n+1 ( x - 4) n . n +1 (- 1)n+1 (x - 4) n + 2 f( x ) dx = . (I got the n + 2 from (n + 1) + 1). (n+ 2)( n + 1)

ゥ (- 1)n+1n ( x - 3) n - 1 ( - 1) n + 1 ( x - 3) n - 1 (b) f( x )=邋 n = n . n=1n5 n = 1 5 (- 1)n+1 (x - 3) n + 1 f( x ) dx = (n+ 1) n 5n

1 a a (6) ,c  4 , our aim is to write this expression in the form = . The first 2  x 1-r 1 - ( x - 4) step is to get the (x - 4) in the denominator: 1 1 = , (equate denominators:0 2-x k - ( x - 4) 2 - x = k - x + 4. (solve for k) -4 -4 -2 = k, so -1 1 1 1 = =* 2 = (to get 1 where the -2 is) 2-x - 2 - ( x - 4) - 2 - ( x - 4) -1 2 -1 2 = (a = -1/2, r = -1/2*(x - 4)) -1 1- (x - 4) 2 骣1 骣 1 n 琪- 琪 -(x - 4) n=0 桫2 桫 2

3 (b) ,c  2 2x 1 3 3 3 = = , 2x- 1 - 1 - - 2 x k - - 2( x - 2) -1 + 2x = k + 2 x - 4, +4 +4 3 = k, so 1 3 3 1 2 =3 = =( - (x - 2))n , 1 2 2x- 1 3 - - 2( x - 2)1- - (x - 2) n=0 3 3 3 1 (7) dx=ln(1 + x ), so we can integrate the given power series to find one for 1+ x ゥ (-x )n+1 ln(1 + x) = 邋(-x )n = . n=0 n = 0 n +1

 n 3 n x 3 (x ) (8) (a) Just plug x3 into  for x: ex = n0 n! n=0 n! x2n+ 1 (4x )2n+ 1 (b) Just plug 4x into (- 1)n+1 for x: (- 1)n+1 n=1 (2n + 1)! n=1 (2n + 1)!

n+1 n n+1 2 n 2 (- 1) (x - 1) (- 1) (x - 1) (c) Just plug x into for x: n=1 n n=1 n