Math 10 Mid-Term Review

1. Simplify the following expressions.

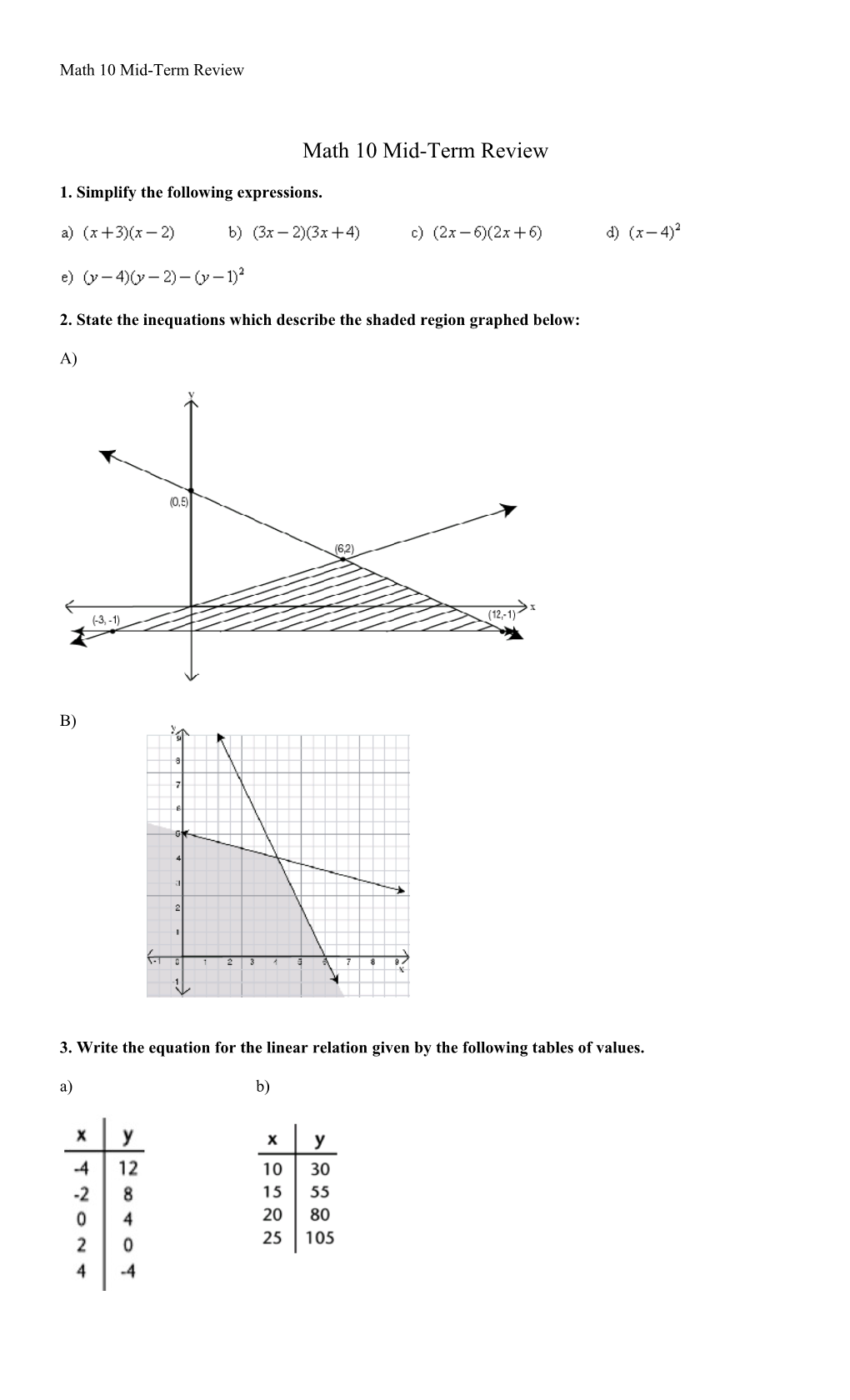
2. State the inequations which describe the shaded region graphed below:

3. Write the equation for the linear relation given by the following tables of values. a) b)

4. Explain the differences in these pairs of graphs:

5. a) State the slope and y- intercept. b) Use the slope and y- intercept to graph the equation.

6. Graph the solution to the system of inequalities

8. Factor the following polynomials:

9. Given the equation 3x - 2y = 12, use the slope and y-intercept to graph the equation.

10. Explain how you know the data in the table below represents a linear relationship.

12. Make a table of values and graph the following: y = 2x + 5

13. Find an expression for the area and perimeter of each of the following rectangles: a) b) c)

14. Solve each of the following.

15. Graph the solution to each system of inequalities:

16. Is the following graph discrete or continuous? Explain why.

17. For the following graphs:

A) Identify the slopes and y-intercepts. B) Determine the equation for each of the graphs.

18. Blair needs to use a taxi to travel 8 km. How much would he save by using the Jolly Green Taxi Company instead of the Big Yellow Taxi Company? Show how you get your solution. 19. Marie made dolls to sell at a craft show. She earned $5 profit for each small doll and $8 for each large doll. Fill in the table to show the profit she made each day of the show.

Day No. of small dolls sold No. of large dolls sold Profit Wednesday 12 15 Thursday 8 22 Friday 20 7 Saturday 10 10

20. Simplify these algebraic expressions.

21. State the domain and range of the following graphs:

22. Write the following expressions in factored form.

23. Give an inequality that describes the region. 24. Use a graph to solve the system.

25. Graph the solution to the system of inequalities:

26. The pro shop makes golf hats and visors. The time required on two machines to make these is shown.

Cutting Machine Stitching Machine Golf Hat 4 minutes 3 minutes Visors 3 minutes 1 minute

The cutting machine is available for at most 2 hours per day and the stitching for only 1 hour per day. They must make at least 6 golf hats each day to keep up with the demand.

If the profit on a golf hat is $1.10 and the profit on a visor is $0.60, calculate how many should be made each day for a maximum profit.

A) Find the constraint equations.

B) Sketch a graph of the feasible region.

C) Find the number of golf hats and visors that the Pro Shop should produce to maximize profit.

27. A student keeps track of the time she spends training for the track team. After 4 days she has spent 13 hours. After 10 days she has spent 31 hours. a) If she has been training at a steady pace since day two, how many hours will she have put in after 16 days? b) How many days until she has put in 100 hours?

28. A student uses his cubes to investigate making T-shapes as shown in the following diagrams:

a) Create a table of values of the T-number versus the number of cubes used for the first 10 T-shapes. b) In words, describe the pattern between the T number and the number of cubes from part A). c) Create a graph of the situation. d) Find an equation that describes the pattern. Let n represent the T-number and c represent the number of cubes used. e) How many cubes are in the 50th T-shape? Justify your answer. f) Is it possible to create a T-shape that consists of exactly 241 cubes? Justify your answer.

29. An automobile has a 25L gasoline tank. At the start of a drive the tank is full, and after traveling 300 km, 20L of gasoline are needed to refill the tank. a) Using technology, sketch a graph of the relationship between distance traveled and the amount of fuel remaining in the tank. b) Give an equation that describes the relation. c) Find the intercept on the horizontal-axis and state its significance. d) How many litres are needed to travel 135 km? 30. Before the snowstorm began, there was 10 cm of old snow already on the ground. The snow fell steadily at a rate of 2 cm every hour. a) Complete this table for the storm

b) Graph the relationship. c) Make up a rule (in words) telling how to find the depth of the snow if you know how long the snow has been falling. d) Write your rule as an equation e) What is the connection between the multiplication in your rule and the story? f) What is the connection between the number you added (in your rule) and the story? g) If the snow starts falling faster, explain how your graph would change? Show this on your graph.

31. Determine the common region on the graphs for the following inequalities.

33. Jane and Bob are planning a large party to celebrate their daughter's success at the Canada Games. As there will be both teens and parents, they contact a local D.J. who is known to play a wide variety of music. For this type of event, the D.J. charges $200 plus $50 per hour. a) Express this relationship in a table of values and a graph. b) If the D.J. plays for 5 hours, what will be the cost? c) Write the equation for the relationship between total cost and the number of hours the D.J. stays at the party. Define any variables that you use. Identify the independent and dependent variables. d) If this D.J. was paid $525, how long did he play at the party?

34. Ryan delivers newspapers before school. While riding his bike he can throw three papers every minute. a) Make a table of values to show the number of papers he delivers over time b) What pattern do you see in the table of values? c) Graph the data from your table of values. d) Is the data discrete or continuous? Explain. e) Explain how the graph displays the pattern shown in the table of values. f) Create an equation that describes this relationship. g) How many papers can he deliver an hour? h) In a set of questions like the above, when is it more useful to use a table of values, a graph, or formula?