Created by Claudia Neuhauser Worksheet 2: Linear Transformations and Linear Regression
Linear Transformations and Linear Regression
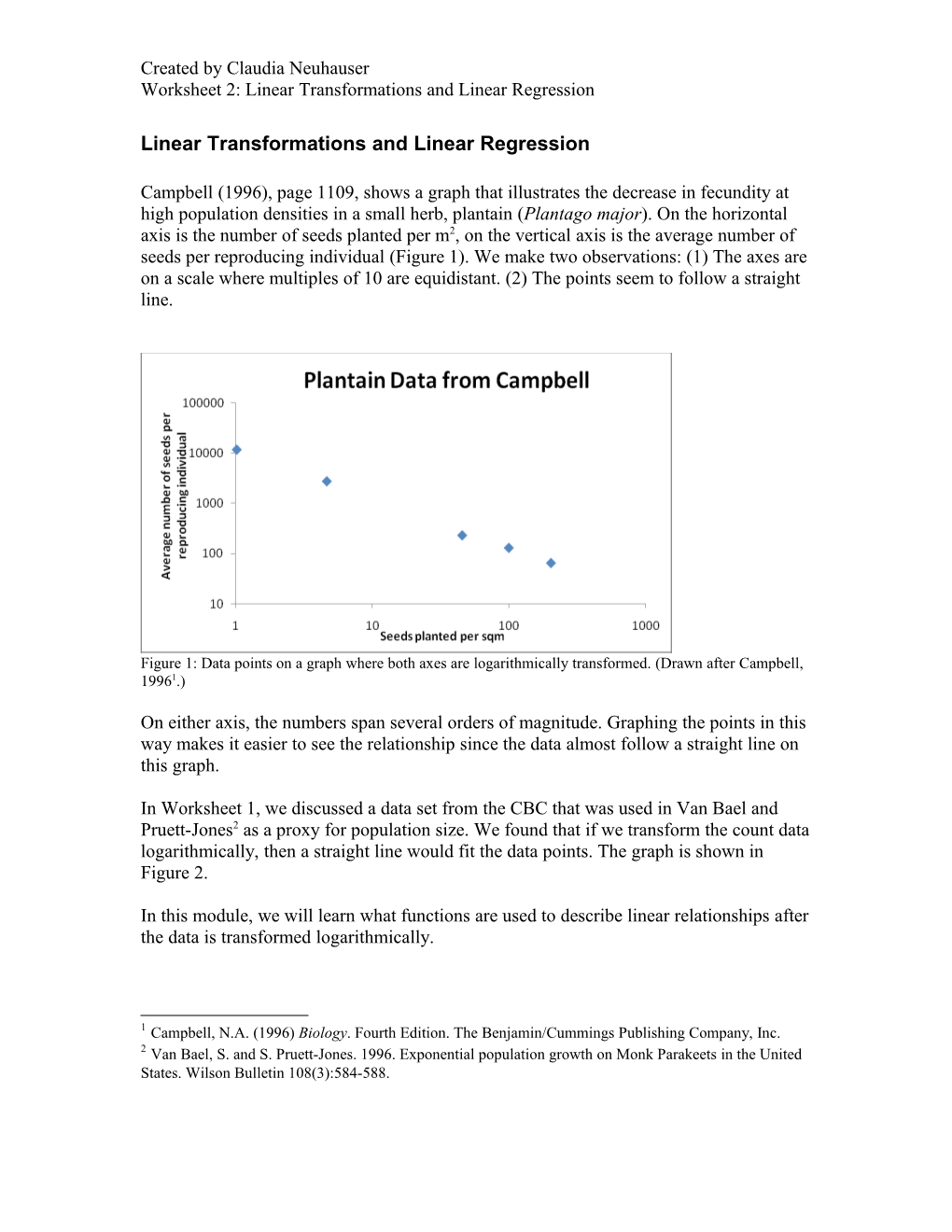
Campbell (1996), page 1109, shows a graph that illustrates the decrease in fecundity at high population densities in a small herb, plantain (Plantago major). On the horizontal axis is the number of seeds planted per m2, on the vertical axis is the average number of seeds per reproducing individual (Figure 1). We make two observations: (1) The axes are on a scale where multiples of 10 are equidistant. (2) The points seem to follow a straight line.
Figure 1: Data points on a graph where both axes are logarithmically transformed. (Drawn after Campbell, 19961.)
On either axis, the numbers span several orders of magnitude. Graphing the points in this way makes it easier to see the relationship since the data almost follow a straight line on this graph.
In Worksheet 1, we discussed a data set from the CBC that was used in Van Bael and Pruett-Jones2 as a proxy for population size. We found that if we transform the count data logarithmically, then a straight line would fit the data points. The graph is shown in Figure 2.
In this module, we will learn what functions are used to describe linear relationships after the data is transformed logarithmically.
1 Campbell, N.A. (1996) Biology. Fourth Edition. The Benjamin/Cummings Publishing Company, Inc. 2 Van Bael, S. and S. Pruett-Jones. 1996. Exponential population growth on Monk Parakeets in the United States. Wilson Bulletin 108(3):584-588. Worksheet 2: Linear Transformations and Linear Regression
Figure 2: Data points on a graph where the vertical axis are logarithmically transformed.
The first step in understanding these relationships is to gain familiarity with logarithms to base 10.
The Logarithmic Scale
A scale where multiples of 10 are equidistant as in the graph above is called a logarithmic scale. It is called logarithmic since the logarithms of the labels on the axis below are equidistant (here: log x or Log x means the logarithm to base 10):
x 0.01 0.1 1 10 100 1000
Log x -2 -1 0 1 2 3
Task 1:
(a) On the two axes above find the following numbers: x=0.05, 0.2, 8, 15, 750. (b) Why do you think we choose logarithms to base 10, instead of some other base? (c) Can you plot negative numbers on a logarithmic scale? (d) As x approaches 0, where would you find x on a logarithmic scale?
2 Worksheet 2: Linear Transformations and Linear Regression
Logarithmic Transformations
The two most frequent transformations of a relationship y f (x) are (1) both axes are logarithmically transformed or (2) the y-axis is logarithmically transformed and the x-axis is on an arithmetic scale. In either case, when such a transformation results in a straight line, we can find the analytical form of the relationship.
Case 1: Both axes are logarithmically transformed
We set X log x and Y log y . If the relationship between Y and X is linear, we can write
Y B aX where B is the Y-intercept and a is the slope. Now, with X log x and Y log y , we get
Y= B + aX logy= B + a log x y =10[B+ a log x ] y =10B 10 alog x 123 a 10log x=x a
With b 10B , we can now write
y bxa
This is a power function. We can summarize this result.
If both axes are logarithmically transformed and a straight line results, then the relationship between x and y is a power function: y bxa
Case 2: The x-axis is on an arithmetic scale and the y-axis is logarithmically transformed
We set Y log y . If the relationship between Y and x is linear, we can write
Y C mx where C is the Y-intercept and m is the slope. Now, with Y log y , we get
3 Worksheet 2: Linear Transformations and Linear Regression
Y C mx log y C mx y 10[Cmx] C mx y 10 10 (10m )x
With c 10C and a 10m , we can now write
y ca x
This is an exponential function. We can summarize this result.
If the x-axis is on an arithmetic scale and the y-axis is logarithmically transformed and a straight line results, then the relationship between x and y is an exponential function: y ca x
Task 2:
(a) Transform the power function y 2x3 so that a straight line results and plot the transformed function. (b) Transform the exponential function y 2.5 3x so that a straight line results and plot the transformed function.
Fitting a Straight Line
Our eyes pick out linear relationships—this is one of the reasons why transformations that result in linear relationships are important. Looking back at Figures 1 and 2, we are tempted to fit straight lines through the points. EXCEL can fit straight lines to data points (see Figures 3 and 4). (The line in Figure 3 is not shown in Campbell.) In Figure 3, we transformed both axes logarithmically. We therefore need to fit a power function. A power function results in a line, and we see in Figure 3 that the line fits almost perfectly. In Figure 4, we only transformed the vertical axis logarithmically. We now need to fit an exponential function. An exponential function results in a line, and we see in Figure 4 that the line fits quite well. In each of these two figures, we display both the functional relationship between the values on the x-axis and y-axis and a quantity R2, which is called the coefficient of determination. The coefficient of determination represents the proportion of variation that is explained by the model. The quantity is therefore always between 0 and 1, and the closer the quantity is to 1, the better the fit. In Figure 3, the value of R2 is 0.997, which is very close to 1, and indeed, the fit is excellent. In Figure 4, the value of R2 is 0.913, which is close to 1, and we see that the fit is quite good, though not as good as in Figure 3.
4 Worksheet 2: Linear Transformations and Linear Regression
Figure 3: A straight line is fitted to the data shown in Figure 1.
Figure 4: A straight line is fitted to the data shown in Figure 2.
IN-CLASS ACTIVITY
Redraw Figures 3 and 4 and fit the appropriate lines. Follow instructions in class. The data are stored in the accompanying spreadsheet under the Tabs “Parakeet” and “Plantain.”
Some Theory (Optional)
There are statistical ways to fit a straight line to a set of points. The idea is that underlying the data, there is a linear model and that random fluctuations cause deviations
5 Worksheet 2: Linear Transformations and Linear Regression from this model. These fluctuations can be measurement errors, for example. Methods have been developed to find lines of “best fit.” The most commonly used one is to minimize the mean squared deviation. Such fits are called least square fits. We call the independent variable x and the dependent variable y. We think of x as being under control of the experimenter (such as “Seeds planted per m2” in Figure 1) and y as the response (such as “Average number of seeds per reproducing individual” in Figure 1). The response y may show random fluctuations. We assume the linear model
y a bx where ε is called the error and represents the random fluctuations. The goal is to estimate a and b from the data where the data consists of points xk , yk , k 1,2,,n . The way this is typically done is to minimize the sum of the squared deviations
n 2 yk a bxk k1
The deviations yk a bxk are called residuals. The method of finding a and b is called the methods of least squares and the resulting line is called the least square line (see Figure 5).
(x , y ) y a bx k k Figurey 5: The line is chosen so that the sum of the squared residuals is minimized. residual The equations for a and b can be found using algebra or calculus. We will not show the y -(a+bx ) details of the computationk here.k They can be found, for instance, in Subsection 12.7.3 in Neuhauser3. We summarize the results.
y k The least square line (or regression line) is given by a+bx k y= aˆ + bxˆ with
n x (x- x )( y - y ) ˆx k =1 k k b =k n (x- x )2 k =1 k aˆ = y - bxˆ
1 n 1 n where x= x and y= y are the arithmetic averages of the x ’s and the n k =1 k n k =1 k k 2 3 Neuhauser,yk’s, respectively. C. (2003) TheCalculus coefficient for Biology of anddetermination Medicine. 2nd Redition. is given Prentice by Hall.
2 轾 (x- x )( y - y ) 2 臌 k6 k R = 2 2 邋(xk- x ) ( y k - y ) Worksheet 2: Linear Transformations and Linear Regression
Homework (Hand in on ______)
In this computer lab you will learn how to enter functions and data, graph them as a scatter plot, and transform the axes logarithmically.
Step 1
Complete Tasks 1 and 2 in this worksheet.
Step 2 For x=1,2,3,…,10, compute f (x) (2.3)x0.7 using a spreadsheet. To do this, set up a spreadsheet as follows:
A B C D 1 x f(x) Log x Log f(x) 2 1 2.3 0 0.361728 3 2 1.415816 0.30103 0.151007 4 3 1.065965 0.477121 0.027743
In Row 1, enter” “x”, “f(x)”, “Log x”, “Log f(x)” as values. Cell A2: “1”, Cell A3” “2”. Drag Cells A2 and A3 down to Row 11. Cell B2: “=2.3*A2^(-0.7)”, Cell C2: “=LOG(A2)”, Cell D2: “=LOG(B2)” Drag Cells B2, C2, and D2 down to Row 11.
Instructions for Office 2003
Step 3 Graph f(x) as a function of x. Click on the “Chart Wizard” and select XY-Scatter. Choose the chart subtype that does not plot lines. Click “Next,” and then “Next” again. Then label the axes of your graph. Click “Next” and “Finish.”
Step 4 Graph Log f(x) as a function of Log x as you did in Step 3.
Step 5 Return to the graph of f(x) as a function of x and change the scale at the axes to logarithmic scales. Compare your graph to the graph you produced in Step 4.
Step 6 You can fit a straight line through the points of your graph by clicking on the points and go to the menu “Chart.” Click on “Add Trendline” and follow the instructions. Try this for both the graphs in Step 4 and Step 5. Click on “Display equation on the Chart.”
7 Worksheet 2: Linear Transformations and Linear Regression
Step 7 For x=1,2,3,…,10, compute f (x) 1.7 x using a spreadsheet. Graph f(x) as a function of x and find a logarithmic transformation that changes the graph into a straight line. Do this by changing the axes. Transform your points so that a straight line results and graph this
Instructions for Office 2007
Step 3 Graph f(x) as a function of x. Click on the “Insert” tab and highlight the values in columns A and B. Select “Scatter” and choose the chart subtype that does not plot lines. Click on the chart and click on the “Layout” tab in the Chart Tools. To label the axes of your graph, select “Axis Titles” in the “Labels” section of the ribbon. Title the graph “Step 3” by selecting the “Chart Title” in the “Labels” section and typing Step 3.
Step 4 Graph Log f(x) as a function of Log x as you did in Step 3.
Step 5 Return to the graph of f(x) as a function of x and change the scale at the axes to logarithmic scales. You can do this under the “Layout” tab. Go to “Axes” and select “More Primary Horizontal Axis Options…” under “Primary Horizontal Axis.” Click on “Logarithmic Scale.” Repeat for the vertical axis. Compare your graph to the graph you produced in Step 4.
Step 6 You can fit a straight line through the points of your graph by clicking on the chart and selecting the “Layout” tab on the “Chart Tools.” Click on “Trendline” and choose “More Trendline Options…” Select the appropriate trendline option for the graphs in Step 4 and Step 5. Click on “Display Equation on chart” and “Display R-squared value on chart.”
Step 7 Show that the equations that are displayed in each graph are what you expected. Explain why R2=1 in both charts.
Step 8 For x=1,2,3,…,10, compute f (x) 1.7 x using a spreadsheet. Graph f(x) as a function of x and find a logarithmic transformation that changes the graph into a straight line. Do this by changing the axes. Then transform the points so that a straight line results if you graphed them and graph this as well. Fit appropriate trendlines and display the equation and R2 in each of the graphs as you did in Step 6. Then show that the equations that are displayed in each graph are what you expected. Explain why R2=1 in both charts.
8 Worksheet 2: Linear Transformations and Linear Regression
Stoichiometry and Homeostasis
Stoichiometry deals with conservation of mass in chemical reactions. This is not only of interest in chemistry but also in ecology where “ecological stoichiometry” refers to a field where predator-prey interactions are viewed through a physiological lens, focusing on element ratios of organisms and their parts. The elements most often considered are carbon, nitrogen and phosphorus. For an animal or plant to grow, it must eat a balanced diet, i.e., a diet that reflects its nutritional needs. Empirical studies have shown that the elemental composition of autotrophs4 often reflect their diet, whereas heterotrophs show constancy of their elemental composition even if their diet is imbalanced. The former is referred to as “absence of homeostasis” whereas the latter is called “strict homeostasis.” These two cases are at the extreme end of what has been observed. Sterner and Elser5 introduce a phenomenological model characterized by one parameter to quantify the degree of homeostasis (see Step 10 below).
The data below are element ratios of food (medium) and element contents or element ratios of the consumer that was reared on that food. The example comes from an autotroph.
Data
This data set is taken from Rhee (1978). It lists the total cell N and P concentrations of the phytoplankton Scenedesmus sp. as a function of the N:P concentration of the medium. The units are cell N (P) x10-6 μg N (P) liter-1 cell-1.
N:P (medium) Cell N Cell P 4.76 0.89 0.37 7.71 1.12 0.41 9.52 1.00 0.22 15.19 1.23 0.19 19.96 1.22 0.14 22.90 1.35 0.13 24.72 1.12 0.10 29.93 1.28 0.09 35.15 1.42 0.09 39.91 1.73 0.10 45.13 1.52 0.07 50.57 1.81 0.09 55.33 1.89 0.08 59.87 2.45 0.09 70.53 2.84 0.09 80.51 3.12 0.09
4 Autotrophs are organisms that synthesize organic compounds from basic elements. Heterotrophs need to consume organic compounds to satisfy their energy needs. 5 Sterner, R.W. and J.J. Elser (2002) Ecological Stoichiometry. Princeton.
9 Worksheet 2: Linear Transformations and Linear Regression
Step 9 Enter the data in a spreadsheet. Compute the Cell N:P ratio and graph the Cell N:P ratio as a function of the medium N:P ratio as an x-y scatter plot. The Sterner and Elser (2002) model is a power function (see Step 10) that related medium N:P to Cell N:P. To fit a straight line, transform both axes logarithmically and use the Trendline option in EXCEL to fit a straight line. The functional relationship is a power function. Find the equation of this function.
Step 10 Sterner and Elser (2002) derived a phenomenological model that is given by the power function
y Cx where y is the consumer stoichiometry (for instance, the N:P ratio) and x is the resource stoichiometry. The parameter θ is important to evaluate whether the cell N:P ratio follows the medium N:P ratio (absence of homeostasis) or whether the organism is able to maintain a fixed ratio of N:P regardless of the medium N:P ratios. Identify the parameter θ based on your results in Step 9 and explain in words why the data suggest absence of homeostasis.
10