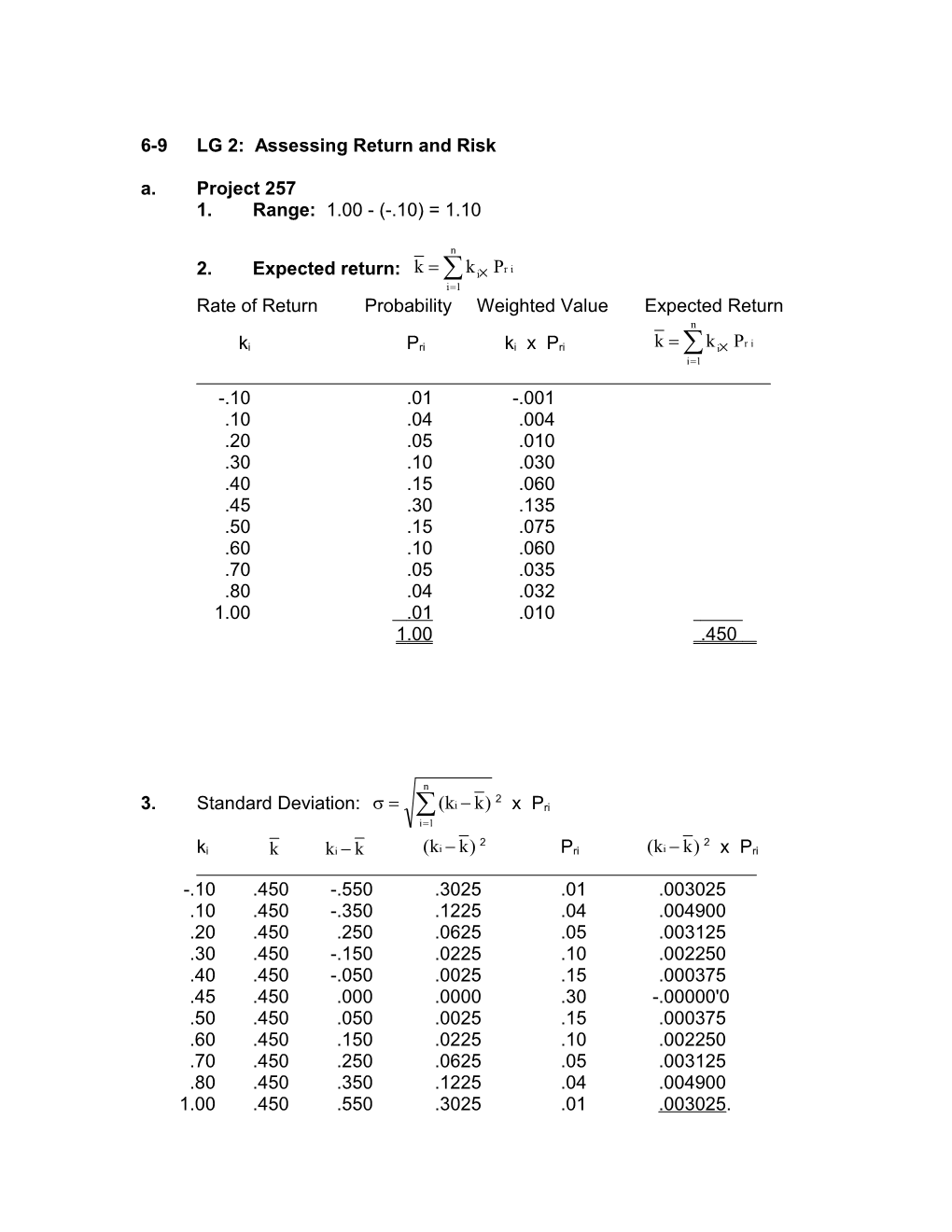
6-9 LG 2: Assessing Return and Risk

6-9 LG 2: Assessing Return and Risk a. Project 257 1. Range: 1.00 - (-.10) = 1.10

n 2. Expected return: k  k i Pr i i1 Rate of Return Probability Weighted Value Expected Return n ki Pri ki x Pri k  k i Pr i i1

-.10 .01 -.001 .10 .04 .004 .20 .05 .010 .30 .10 .030 .40 .15 .060 .45 .30 .135 .50 .15 .075 .60 .10 .060 .70 .05 .035 .80 .04 .032 1.00 .01 .010 1 .00 .450

n 2 3. Standard Deviation:   (ki  k) x Pri i1 2 2 ki k ki  k (ki  k) Pri (ki  k) x Pri

-.10 .450 -.550 .3025 .01 .003025 .10 .450 -.350 .1225 .04 .004900 .20 .450 .250 .0625 .05 .003125 .30 .450 -.150 .0225 .10 .002250 .40 .450 -.050 .0025 .15 .000375 .45 .450 .000 .0000 .30 -.00000'0 .50 .450 .050 .0025 .15 .000375 .60 .450 .150 .0225 .10 .002250 .70 .450 .250 .0625 .05 .003125 .80 .450 .350 .1225 .04 .004900 1.00 .450 .550 .3025 .01 .003025. .027350

Project 257 = .027350 = .165378

.165378 4. CV   .3675 .450 Project 432

1. Range: .50 - .10 = .40

n 2. Expected return: k  k i Pr i i1 Rate of Return Probability Weighted Value Expected Return n ki Pri ki x Pri k   ki Pr i i1

.10 .05 .0050 .15 .10 .0150 .20 .10 .0200 .25 .15 .0375 .30 .20 .0600 .35 .15 .0525 .40 .10 .0400 .45 .10 .0450 .50 .05 .0250 1 .00 .300

n 2 3. Standard Deviation:   (ki  k) x Pri i1 2 2 ki k ki  k (ki  k) Pri (ki  k) x Pri

.10 .300 -.20 .0400 .05 .002000 .15 .300 -.15 .0225 .10 .002250 .20 .300 -.10 .0100 .10 .001000 .25 .300 -.05 .0025 .15 .000375 .30 .300 .00 .0000 .20 .000000 .35 .300 .05 .0025 .15 .000375 .40 .300 .10 .0100 .10 .001000 .45 .300 .15 .0225 .10 .002250 .50 .300 .20 .0400 .05 .002000 .011250 Project 432 = .011250 = .106066

.106066 4. CV   .3536 .300

b. Bar Charts Project 257

0.15 Probability 0.1

0 -10% 10% 20% 30% 40% 45% 50% 60% 70% 80% 100%

Rate of Return

Project 432

0.1 Probability 0.08

0 10% 15% 20% 25% 300% 35% 40% 45% 50%

Rate of Return c. Summary Statistics

Project 257 Project 432 Range 1.100 .400 Expected Return ( k ) 0.450 .300 Standard Deviation ( k ) 0.165 .106 Coefficient of Variation (CV) 0.3675 .3536

Since Projects 257 and 432 have differing expected values, the coefficient of variation should be the criterion against which the risk of the asset is judged. Since Project 432 has a smaller CV, it is the opportunity with lower risk.

6-10 LG 2: Integrative-Expected Return, Standard Deviation, and Coefficient of Variation

n a. Expected return: k  ki  Pr i i1

Rate of Return Probability Weighted Value Expected Return n ki Pri ki x Pri k  k i Pr i i1

Asset F .40 .10 .04 .10 .20 .02 .00 .40 .00 -.05 .20 -.01 -.10 .10 -.01 .04

Asset G .35 .40 .14 .10 .30 .03 -.20 .30 -.06 .11

Asset H .40 .10 .04 .20 .20 .04 .10 .40 .04 .00 .20 .00 -.20 .10 -.02 .10

Asset G provides the largest expected return.

n 2 b. Standard Deviation: k  (ki  k) x Pri i1 2 2 (ki  k) (ki  k) Pri  k

Asset F .40 - .04 = .36 .1296 .10 .01296 .10 - .04 = .06 .0036 .20 .00072 .00 - .04 = -.04 .0016 .40 .00064 -.05 - .04 = -.09 .0081 .20 .00162 -.10 - .04 = -.14 .0196 .10 .00196 .01790 .1338

Asset G .35 - .11 = .24 .0576 .40 .02304 .10 - .11 = -.01 .0001 .30 .00003 -.20 - .11 = -.31 .0961 .30 .02883 .05190 .2278

2 2 (ki  k) (ki  k) Pri  k

Asset H.40 - .10 = .30 .0900 .10 .009 .20 - .10 = .10 .0100 .20 .002 .10 - .10 = -.10 .0000 -.40 .000 .00 - .10 = -.10 .0100 .20 .002 -.20 - .10 = -.30 .0900 .10 .009 .022 .1483

Based on standard deviation, Asset G appears to have the greatest risk, but it must be measured against its expected return with the statistical measure coefficient of variation, since the three assets have differing expected values. An incorrect conclusion about the risk of the assets could be drawn using only the standard deviation.

standard deviation () c. Coefficient of Variation = expected value .1338 Asset F: CV   3.345 .04

.2278 Asset G: CV   2.071 .11

.1483 Asset H: CV  1.483 .10

As measured by the coefficient of variation, Asset F has the largest relative risk.

6-12 LG 3: Portfolio Return and Standard Deviation a. Expected Portfolio Return for Each Year: kp = (wL x kL) + (wM x kM)

Expected Asset L Asset M Portfolio Return Year (wL x kL) + (wM x kM) kp

1998 (14% x.40 =5.6%) + (20% x .60 =12.0%) = 17.6% 1999 (14% x.40 =5.6%) + (18% x .60 =10.8%) = 16.4% 2000 (16% x.40 =6.4%) + (16% x .60 = 9.6%) = 16.0% 2001 (17% x.40 =6.8%) + (14% x .60 = 8.4%) = 15.2% 2002 (17% x.40 =6.8%) + (12% x .60 = 7.2%) = 14.0% 2003 (19% x.40 =7.6%) + (10% x .60 = 6.0%) = 13.6%

n  wj  kj b. Portfolio Return: j1 kp  n

17.6 16.4 16.0 15.2 14.0 13.6 kp  15.467 15.5% 6

n 2 (ki  k) c. Standard Deviation: kp   i1 (n  1)

(17.6% 15.5%)2  (16.4% 15.5%)2  (16.0% 15.5%)2   2 2 2   (15.2% 15.5%)  (14.0% 15.5%)  (13.6% 15.5%)  kp  6 1 (2.1%)2  (.9%)2  (0.5%)2   2 2 2   (.3%)  (1.5%)  (1.9%)  kp  5

(4.41%  .81%  0.25%  .09%  2.25%  3.61%) kp  5

11.42 kp   2.284 1.51129 5 d. The assets are negatively correlated. e. Combining these two negatively correlated asset reduces overall portfolio risk.

6-13 LG 3: Portfolio Analysis a. Expected portfolio return:

Alternative 1: 100% Asset F

16% 17% 18% 19% kp   17.5% 4

Alternative 2: 50% Asset F + 50% Asset G

Asset F Asset G Portfolio Return Year (wF x kF) + (wG x kG) kp

2001 (16% x .50 = 8.0%) + (17% x .50 = 8.5%) = 16.5% 2002 (17% x .50 = 8.5%) + (16% x .50 = 8.0%) = 16.5% 2003 (18% x .50 = 9.0%) + (15% x .50 = 7.5%) = 16.5% 2004 (19% x .50 = 9.5%) + (14% x .50 = 7.0%) = 16.5%

66 kp  16.5% 4

Alternative 3: 50% Asset F + 50% Asset H

Asset F Asset H Portfolio Return Year (wF x kF) + (wH x kH) kp

2001 (16% x .50 = 8.0%) + (14% x .50 = 7.0%) 15.0% 2002 (17% x .50 = 8.5%) + (15% x .50 = 7.5%) 16.0% 2003 (18% x .50 = 9.0%) + (16% x .50 = 8.0%) 17.0% 2004 (19% x .50 = 9.5%) + (17% x .50 = 8.5%) 18.0%

66 kp  16.5% 4

n 2 (ki  k) b. Standard Deviation: kp   i1 (n  1) (1)

(16.0% 17.5%)2  (17.0% 17.5%)2  (18.0% 17.5%)2  (19.0% 17.5%)2  F  4 1

(-1.5%)2  (.5%)2  (0.5%)2  (1.5%)2  F  3

(2.25%  .25%  .25%  2.25%) F  3

5 F   1.667 1.291 3

(2) (16.5% 16.5%)2  (16.5% 16.5%)2  (16.5% 16.5%)2  (16.5% 16.5%)2  FG  4 1

(0)2  (0)2  (0)2  (0)2  FG  3

FG  0

(3) (15.0%  16.5%) 2  (16.0%  16.5%) 2  (17.0%  16.5%) 2  (18.0%  16.5%) 2  FH  4  1 (1.5%)2  (0.5%)2  (0.5%)2  (1.5%)2  FH  3

(2.25  .25  .25  2.25) FH  3

5 FH   1.667 1.291 3 c. Coefficient of variation: CV = k  k

1.291 CVF   .0738 17.5%

0 CVFG   0 16.5%

1.291 CVFH   .0782 16.5% d. Summary:

kp: Expected Value

of Portfolio kp CVp

Alternative 1 (F) 17.5% 1.291 .0738 Alternative 2 (FG) 16.5% -0- .0 Alternative 3 (FH) 16.5% 1.291 .0782 Since the assets have different expected returns, the coefficient of variation should be used to determine the best portfolio. Alternative 3, with positively correlated assets, has the highest coefficient of variation and therefore is the riskiest. Alternative 2 is the best choice; it is perfectly negatively correlated and therefore has the lowest coefficient of variation.

6-20 LG 5: Betas and Risk Rankings a. Stock Beta Most risky B 1.40 A 0.80 Least risky C -0.30 b. and c. Increase in Expected Impact Decrease in Impact on Asset Beta Market Return on Asset Return Market Return Asset Return A 0.80 .12 .096 -.05 -.04 B 1.40 .12 .168 -.05 -.07 C - 0.30 .12 -.036 -.05 .015 d. In a declining market, an investor would choose the defensive stock, Stock C. While the market declines, the return on C increases. e. In a rising market, an investor would choose Stock B, the aggressive stock. As the market rises one point, Stock B rises 1.40 points.

n 6-21 LG 5: Portfolio Betas: bp =  wj  bj j1 a. Asset Beta wA wA x bA wB wB x bB

A 1.30 .10 .130 .30 .39 B 0.70 .30 .210 .10 .07 C 1.25 .10 .125 .20 .25 D 1.10 .10 .110 .20 .22 E .90 .40 .360 .20 .18 bA = .935 bB = 1 .11 b. Portfolio A is slightly less risky than the market (average risk), while Portfolio B is more risky than the market. Portfolio B's return will move more than Portfolio A’s for a given increase or decrease in market risk. Portfolio B is the more risky.

6-22 LG 6: Capital Asset Pricing Model: kj = RF + [bj x (km - RF)]

Case kj = RF + [bj x (km - RF)]

A 8.9% = 5% + [1.30 x (8% - 5%)] B 12.5% = 8% + [0.90 x (13% - 8%)] C 8.4% = 9% + [- 0.20 x (12% - 9%)] D 15.0% = 10% + [1.00 x (15% - 10%)] E 8.4% = 6% + [0.60 x (10% - 6%)]

6-23 LG 5, 6: Beta Coefficients and the Capital Asset Pricing Model

To solve this problem you must take the CAPM and solve for beta. The resulting model is: k  RF Beta  km  RF 10%  5% 5% a. Beta    .4545 16%  5% 11%

15%  5% 10% b. Beta    .9091 16%  5% 11%

18%  5% 13% c. Beta   1.1818 16%  5% 11%

20%  5% 15% d. Beta   1.3636 16%  5% 11% e. If Katherine is willing to take a maximum of average risk then she will only be able to have an expected return of 16%. k = 5% + 1.0(16% - 5%) = 16%.