Worksheet on Applications of the Definite Integral

CALCULUS BC WORKSHEET ON APPLICATIONS OF THE DEFINITE INTEGRAL

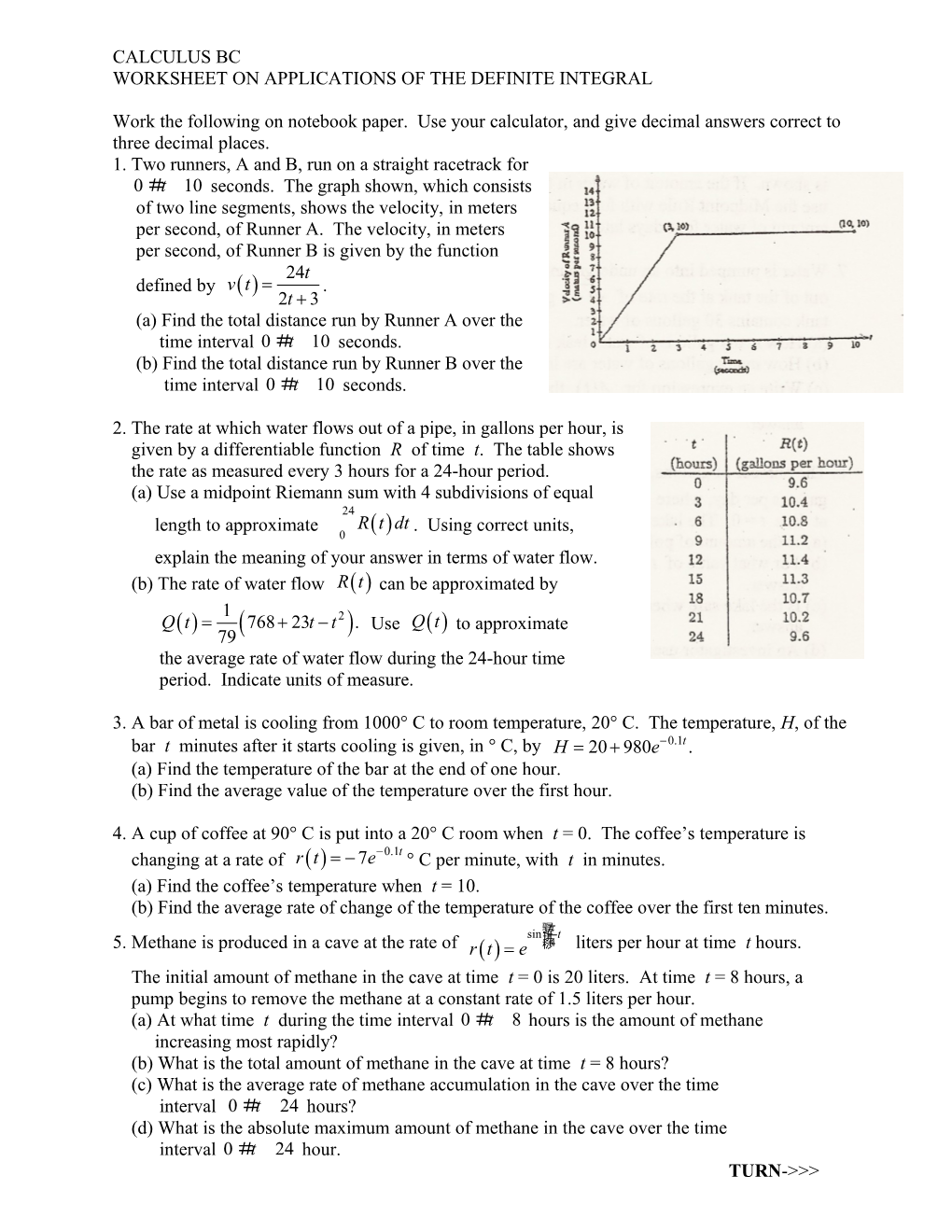
Work the following on notebook paper. Use your calculator, and give decimal answers correct to three decimal places. 1. Two runners, A and B, run on a straight racetrack for 0＃t 10 seconds. The graph shown, which consists of two line segments, shows the velocity, in meters per second, of Runner A. The velocity, in meters per second, of Runner B is given by the function 24t defined by v( t) = . 2t + 3 (a) Find the total distance run by Runner A over the time interval 0＃t 10 seconds. (b) Find the total distance run by Runner B over the time interval 0＃t 10 seconds.

2. The rate at which water flows out of a pipe, in gallons per hour, is given by a differentiable function R of time t. The table shows the rate as measured every 3 hours for a 24-hour period. (a) Use a midpoint Riemann sum with 4 subdivisions of equal 24 length to approximate R t dt . Using correct units, 0 ( ) explain the meaning of your answer in terms of water flow. (b) The rate of water flow R( t) can be approximated by 1 Q( t) =(768 + 23 t - t 2 ) . Use Q( t) to approximate 79 the average rate of water flow during the 24-hour time period. Indicate units of measure.

3. A bar of metal is cooling from 1000° C to room temperature, 20° C. The temperature, H, of the bar t minutes after it starts cooling is given, in ° C, by H=20 + 980 e-0.1t . (a) Find the temperature of the bar at the end of one hour. (b) Find the average value of the temperature over the first hour.

4. A cup of coffee at 90° C is put into a 20° C room when t = 0. The coffee’s temperature is changing at a rate of r( t) = - 7 e-0.1t ° C per minute, with t in minutes. (a) Find the coffee’s temperature when t = 10. (b) Find the average rate of change of the temperature of the coffee over the first ten minutes. 骣p sin琪 t 5. Methane is produced in a cave at the rate of r( t) = e 桫4 liters per hour at time t hours. The initial amount of methane in the cave at time t = 0 is 20 liters. At time t = 8 hours, a pump begins to remove the methane at a constant rate of 1.5 liters per hour. (a) At what time t during the time interval 0＃t 8 hours is the amount of methane increasing most rapidly? (b) What is the total amount of methane in the cave at time t = 8 hours? (c) What is the average rate of methane accumulation in the cave over the time interval 0＃t 24 hours? (d) What is the absolute maximum amount of methane in the cave over the time interval 0＃t 24 hour. TURN->>> 6. Water flows in and out of a storage tank. A graph of the rate of change r( t) of the volume of water in the tank, in liters per day, is shown. If the amount of water in the tank at time t = 0 is 25,000L, use the Midpoint Rule with four equal subintervals to estimate the amount of water four days later.

7. Water is pumped into an underground tank at a constant rate of 8 gallons per minute. Water leaks out of the tank at the rate of t +1 gallons per minute, for 0＃t 120 minutes. At time t = 0, the tank contains 30 gallons of water. (a) How many gallons of water leak out of the tank from time t = 0 to t = 3 minutes? (b) How many gallons of water are in the tank at time t = 3 minutes? (c) Write an expression for A( t ) , the total number of gallons of water in the tank at time t. (d) At what time t, for 0＃t 120 , is the amount of water in the tank a maximum? Justify your answer.

8. The number of gallons, P( t) , of a pollutant in a lake changes at the rate P( t) =1 - 3 e-0.2 t gallons per day, where t is measured in days. There are 50 gallons of the pollutant in the lake at time t = 0. The lake is considered to be safe when it contains 40 gallons or less of pollutant. (a) Is the amount of pollutant increasing at time t = 9? Why or why not? (b) For what value of t will the number of gallons of pollutant be at its minimum? Justify your answer. (c) Is the lake safe when the number of gallons of pollutant is at its minimum? Justify your answer. (d) An investigator uses the tangent line approximation to P( t) at t = 0 as a model for the amount of pollutant in the lake. At what time t does this model predict that the lake becomes safe?

9. A particle moves along the x-axis so that its velocity v at any time t, for 0＃t 4 , is given by v( t) = e2sint -1. At time t = 0, the particle is at the point (-1, 0) . (a) For what values of t, 0＃t 4 , is the particle moving to the right? to the left? (b) Find the position of the particle at t = 4. (c) Find the total distance traveled by the particle from t = 0 to t = 4. Answers 1. (a) 85 meters (b) 83.336 meters 2. (a) 258.6 gallons (b) 10.785 gal/hr 3. (a) 22.429°C (b) 182.928°C 4. (a) 45.752°C (b) – 4.425°C/min 5. (a) 2 hours (b) 30.129 liters (c) 0.266 liters/hr (d) 32.174 liters 6. 28.250 liters 2 1 t 7. (a) 4 gallons (b) 49 gallons (c) A( t) =30 + 8 t - x + 1 dx 3 3 0 (d) 63 minutes 8. (a) decreasing, not increasing (b) 30.174 days (c) The lake is safe. (d) 5 days 9. (a) Right for 0 � t 3.142 and left for 3.142< t 4 (b) 8.671 (c) 10.542